Skew normal distribution
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

The Holmfirth floods were a number of instances when severe flooding had occurred in the Holme Valley, West Yorkshire, England affecting Holmfirth and other settlements in the valley. The earliest record dates from 1738 and the latest from 1944. The most severe flood occurred early on the morning of 5 February 1852, when the embankment of the Bilberry reservoir collapsed causing the deaths of 81 people. It is recorded as the 23rd most serious, worldwide, in terms of loss of life from floods a...

Doarp Grou Lengte 19,36 m Breedte 3,63 m Diepgang 0,43 m Bemanning ± 12 personen Zeilen Zeiloppervlakte 164,8 m² Ontwerp Jaar 1909 Zeilteken Portaal Maritiem Doarp Grou is het skûtsje waarmee een vertegenwoordiging van het Friese dorp Grouw (Fries: Grou) deelneemt aan de wedstrijden van de Sintrale Kommisje Skûtsjesilen. Het is het tweede skûtsje waarmee Grou meedoet aan de wedstrijden. Het eerste skûtsje kochten ze in 1957, maar hebben ze al na een jaar al weer vervangen d...

Lukisan sapi Lascaux Kuda Lascaux Lukisan Lascaux adalah lukisan dinding yang terletak di gua Lascaux di Dordogne di Prancis.[1] Lukisan dinding ini menggambarkan banyak spesies hewan dan gambar manusia yang dilukis dengan warna tanah berpigmen coklat, hitam, kuning dan merah.[1][2] Pigmen-pigmen ini dihasilkan dari oker, hematit, dan mangan yang digambarkan pada permukaan dinding batu kapur yang berwarna putih.[1] Seniman Lascaux menciptakan gambar-gambar ini ...

Villa Nora, 2019, Ansicht von der Kortumstraße Die Villa Nora ist eine ehemalige Unternehmervilla an der Kortumstraße 156 im Stadtparkviertel in Bochum.[1] Sie wurde 1897 bis 1899 für Heinrich Koehler, Generaldirektor der westfälischen Stahlwerke, errichtet. Den Namen erhielt sie durch den Kosenamen von Koehlers Frau Amélie. Heute befindet sich die Villa im Besitz einer Stiftung der Sparkasse Bochum und wird unter anderem für das gegenüberliegende Kunstmuseum Bochum genutzt. Da...

Kamehameha IV Rey de Hawái Kamehameha IV de Hawái.Reinado 11 de enero de 1856-30 de noviembre de 1863(8 años)Predecesor Kamehameha IIISucesor Kamehameha VInformación personalNombre completo Alekanetero (Alexander) ʻIolani Liholiho Kalanikualiholiho MakaCoronación 11 de enero de 1855Nacimiento 9 de febrero de 1834Honolulu, HawáiFallecimiento 30 de noviembre de 1863 (29 años)Honolulu, HawáiSepultura Mausoleo Real de HawáiFamiliaDinastía Casa de KamehamehaPadre KekūanaōʻaMadre...

هذه قائمة بالأفلام والمسلسلات التلفزيونية من وجهة نظر إسلامية، والمتعلقة بالحضارة الإسلامية، أي الإسلام والتاريخ الإسلامي والثقافة الإسلامية، تميل أغلب الأفلام والمسلسلات إلى تصوير المرأة بالحجاب، وتتوفر معظمها مع ترجمات ودبلجة بلغات متعددة.[1][2][3] مسلسلات...

Overview of the events of 1913 in music 1913 in music By location United Kingdom Norway By genre jazz By topic Overview of the events of 1913 in music List of years in music (table) … 1903 1904 1905 1906 1907 1908 1909 1910 1911 1912 1913 1914 1915 1916 1917 1918 1919 1920 1921 1922 1923 … In film 1910 1911 1912 1913 1914 1915 1916 In radio 1910 1911 1912 1913 1914 1915 1916 Art Archaeology Architecture Literature Music Philosophy Science +... This is a list of notable events in music tha...

Fountain L. Thompson Fountain Land Thompson (* 18. November 1854 bei Scottville, Macoupin County, Illinois; † 4. Februar 1942 in Los Angeles) war ein US-amerikanischer Politiker (Demokratische Partei), der den Bundesstaat North Dakota im US-Senat vertrat. Der in der Nähe von Scottville geborene Thompson zog 1865 mit seiner Familie nach Girard, wo er die öffentlichen Schulen besuchte und die Rechte studierte. Zwar wurde er in die Anwaltskammer aufgenommen, arbeitete aber praktisch nicht in...

Genus of moths Comostola Comostola laesaria Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Lepidoptera Family: Geometridae Tribe: Hemitheini Genus: ComostolaMeyrick, 1888 Synonyms Pyrrhorachis Warren, 1896 Leucodesmia Warren, 1899 (preocc. Howard, 1895) Chloeres Turner, 1910 Comostola is a genus of moths in the family Geometridae erected by Edward Meyrick in 1888. They are found primarily in Asia and Australia.[1] Species Comosto...

16th-century monumental woodcut print The Triumphal Arch Detail of pinnacle from a coloured impression in Brunswick. The Triumphal Arch (also known as the Arch of Maximilian I, German: Ehrenpforte Maximilians I.) is a 16th-century monumental woodcut print commissioned by the Holy Roman Emperor Maximilian I. The composite image was printed on 36 large sheets of paper from 195 separate wood blocks. At 295 × 357 centimetres (116 × 141 in), it is one of the largest prin...

У Вікіпедії є статті про інших людей із прізвищем Фединський Юрій. Фединський Юрій Народився 1975СШАКраїна СШАДіяльність композитор, виробник музичних інструментів Юрій Фединський (1975, США) — бандурист, композитор, що займається українською кобзарською традиціє�...

هنري ستانلي بلومر معلومات شخصية الميلاد 3 مارس 1874(1874-03-03)مينيسوتا الوفاة 31 ديسمبر 1936 (62 سنة)روتشيستر، مينيسوتا مواطنة الولايات المتحدة الأمريكية الأب ألبرت بلامر الحياة العملية المدرسة الأم جامعة نورث وسترنجامعة الشمال الغربي مدرسة فينبرغ للطب المهنة طبيب باطني &...

2014 animated film AnahitDirected byDavit SahakyantsScreenplay byDavit SahakyantsNaira SahakyantsLyulya SahakyantsMusic byArmen MartirosyanVardan ZadoyanProductioncompanyRobert Sahakyants ProductionRelease date27 December 2014Running time90 minutesCountryArmeniaLanguageArmenian Anahit is a 2014 Armenian traditionally animated fantasy film directed by Davit Sahakyants, based on a screenplay by Davit, Naira Sahakyants and Lyulya Sahakyants (who also acted as co-director). The screenplay was bas...

Ця стаття не містить посилань на джерела. Ви можете допомогти поліпшити цю статтю, додавши посилання на надійні (авторитетні) джерела. Матеріал без джерел може бути піддано сумніву та вилучено. (квітень 2018) Спортивний симулятор (англ. sports game) — це жанр відеоігор, основ...

2015 film score by Christophe BeckAnt-Man (Original Motion Picture Soundtrack)Film score by Christophe BeckReleased July 17, 2015 (2015-07-17) (Digital) August 7, 2015 (2015-08-07) (Physical) GenreFilm scoreLength1:05:20Label Hollywood Marvel Music Christophe Beck chronology Hot Pursuit(2015) Ant-Man (Original Motion Picture Soundtrack)(2015) The Peanuts Movie(2015) Marvel Cinematic Universe soundtrack chronology Avengers: Age of Ultron(2015) Ant-Man(2015...

American college football rivalry Houston–Tulsa football rivalry Houston Cougars Tulsa Golden Hurricane First meetingDecember 2, 1950Tulsa, 28–21Latest meetingNovember 26, 2022Tulsa, 37–30Next meetingTBDStatisticsMeetings total46All-time seriesHouston leads, 26–20[1]Largest victoryHouston, 100–6 (1968)Longest win streakHouston, 5 (1968–1973)Current win streakTulsa, 1 (2022–present) [Interactive fullscreen map + nearby articles] Locations of Houston and Tulsa The Houston�...

Locality in Castile and León, SpainLago de BabiaLocalityLago de BabiaShow map of Province of LeónLago de BabiaShow map of Castile and LeónLago de BabiaShow map of SpainCoordinates: 42°58′10″N 6°10′48″W / 42.96944°N 6.18000°W / 42.96944; -6.18000[1]Country SpainAutonomous community Castile and LeónProvinceProvince of LeónMunicipalityCabrillanesElevation1,345 m (4,413 ft)Population • Total24 Lago de Babia (Astur-Le...

Family of the modernized version of AK-47 Assault rifle For other uses, see AKM (disambiguation). This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (September 2018) AKM Both sides of the AKMTypeAssault riflePlace of originUSSRService historyIn service1959–presentUsed bySee UsersWarsSee ConflictsProduction historyDesignerMikhail ...

Bristol-Coanda Monoplanes Role TrainerType of aircraft Manufacturer Bristol Aeroplane Company Designer Henri Coandă First flight 1912 Number built 37 Variants Bristol TB.8 The Bristol Coanda Monoplanes were a series of monoplane trainers designed by the Romanian designer Henri Coandă for the British company British and Colonial Aeroplane Company. Several versions of the plane were built from 1912 onwards with both tandem and side-by-side cockpits. Several were purchased by the War Office fo...

Halaman ini berisi artikel tentang permaisuri Raja Kamehameha VI dari Hawaii. Untuk ratu yang bernama sama, lihat Ratu Emma. Ratu Emma. Emma Kalanikaumakaamano Kaleleonalani Naea Rooke, Ratu Hawaii (2 Januari 1836 – 25 April 1885) adalah permaisuri Raja Kamehameha IV dari tahun 1856 sampai wafatnya raja pada tahun 1863. Ia mencoba mengangkat dirinya sebagai Ratu melawan Raja David Kalakaua. Masamuda Emma dilahirkan dengan nama Emalani,[1] dan belakangan namanya menjadi...
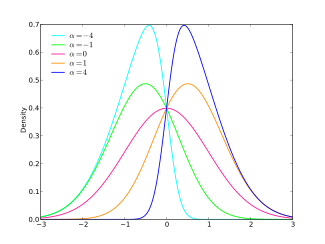
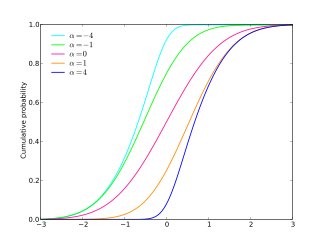

















![{\displaystyle \Phi (x)=\int _{-\infty }^{x}\phi (t)\ \mathrm {d} t={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d25fac22a180c95ddcf8339c45364fced5b1302)



































