Natural exponential family
|
Read other articles:

Cal Poly PomonaCollege of Business AdministrationMottoInstrumentum Disciplinae (Latin: Application of Knowledge)TypePublic College Space Grant[1]Established1968; 55 years ago (1968)[2]Parent institutionCal Poly PomonaAcademic affiliationsAACSB InternationalDeanErik Rolland [3]Academic staff146 (2001)[4]Administrative staff90Students4,919 (Fall 2016)[5] (percent of total university enrollment: 19%)Undergraduates4,876 (Fall 2016)Postgrad...

Léo Collard Leo Collard in 1968 Volledige naam Léo Jules Emile Collard[1] Geboren Aulnois, 11 juli 1902 Overleden Bergen, 27 januari 1981 Kieskring Bergen Regio Wallonië Land België Partij POB / PSB Functies 1933-1976 Gemeenteraadslid Bergen 1932-1971 Volksvertegenwoordiger 1946 Minister van Openbaar Onderwijs 1947-1952 Schepen Bergen 1953-1974 Burgemeester Bergen 1954-1958 Minister van Openbaar Onderwijs 1980-1982 Partijvoorzitter BSP-PSB Portaal België Politi...

В данной статье описаны второстепенные географические объекты, описанные в произведениях, являющихся частью легендариума Дж. Р. Р. Толкина. Содержание 1 А 1.1 Аваллонэ 1.2 Аватар 1.3 Агларонд 1.4 Азанулбизар 1.5 Алмарен 1.6 Амон Лау 1.7 Амон Обел 1.8 Амон Руд 1.9 Амон Сул 1.10 Амон Х�...

Group of Indo-Aryan languages Pahari languages redirects here. Not to be confused with Pahari language. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Northern Indo-Aryan languages – news · newspapers · books · scholar · JSTOR (October 2011) (Learn how and when to remove this template message) Northern Indo...
هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها. هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2013) اختصاصية حياة الأطفال اختصاصيو حياة الطفل هم اختصاصيو الرع
Esslingen Brasão de Esslingenbrasão Localização de Esslingen na Alemanhamapa Dados Estado Baden-Württemberg Capital Esslingen Região Adm. Estugarda Área 641,57 km² População (31/12/2007) 514.503 hab. Densidade 802 hab/km² Website www.landkreis-esslingen.de Administração distrital Endereço Pulverwiesen 1173728 Esslingen Administrador Heinz Eininger Localização no Estado Esslingen ou, na sua forma portuguesa, Eslinga[1] é um distrito da Alemanha, na região administrativa de Es...

1931 film This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Son of India 1931 film – news · newspapers · books · scholar · JSTOR (April 2012) (Learn how and when to remove this template message) Son of IndiaTheatrical posterDirected byJacques FeyderScreenplay byErnest VajdaJohn MeehanClaudine WestBased on...

Simbabwe Kapitän Freeman Nyamunokora Aktuelles ITF-Ranking 80 Statistik Erste Teilnahme 1963 Davis-Cup-Teilnahmen 35 davon in Weltgruppe 3 Bestes Ergebnis VF (1998) Ewige Bilanz 41:43 Erfolgreichste Spieler Meiste Siege gesamt Byron Black (56) Meiste Einzelsiege Byron Black (39) Meiste Doppelsiege Wayne Black (19) Bestes Doppel Wayne Black / Byron Black (10) Meiste Teilnahmen Byron Black (31) Meiste Jahre Byron Black (15) Letzte Aktualisierung der Infobox: 14. März 2012 Die simbabwische Dav...

Front Pembebasan Islam MoroBendera Front Pembebasan Islam MoroPemimpinNur Misuari, Haji Murad Ibrahim (mantan), Sheikh Hashim Salamat (mantan)Waktu operasi1978 – 27 Maret 2014 (Gencatan senjata permanen)[1]MarkasDarapanan, Sultan Kudarat, MaguindanaoWilayah operasiMindanao, FilipinaIdeologiDemokrasi IslamPertempuran dan perangKonflik Moro Front Pembebasan Islam Moro (bahasa Inggris: Moro Islamic Liberation Front/MILF; Arab: جبهة تحرير مورو...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2019) دان بيريس معلومات شخصية الميلاد 14 أكتوبر 1971 (52 سنة) مواطنة الولايات المتحدة الزوجة ساره وينتر (2005–) الحياة العملية المدرسة الأم جامعة نيويورك الم

Manuel Obafemi Akanji Akanji bermain untuk Swiss di Piala Dunia FIFA 2018Informasi pribadiNama lengkap Manuel Obafemi Akanji[1]Tanggal lahir 19 Juli 1995 (umur 28)Tempat lahir Wiesendangen,[2] SwissTinggi 188 cm (6 ft 2 in)[3]Posisi bermain BekInformasi klubKlub saat ini Manchester CityNomor 25Karier junior2004–2007 FC Wiesendangen2007–2014 WinterthurKarier senior*Tahun Tim Tampil (Gol)2013–2014 Winterthur II 18 (0)2014–2015 Winterthur 35 (1...

This article is about relations with the Republic of China. For relations between the People's Republic of China and the United Kingdom, see China–United Kingdom relations. Bilateral relationsTaiwan–United Kingdom relations Taiwan United Kingdom Diplomatic missionTaipei Representative Office in the U.K.British Office TaipeiEnvoyKelly Wu-Chiao HsiehJohn Dennis Taipei Representative Office in the U.K. Taiwan–United Kingdom relations refers to bilateral relations between Taiwan (officially...

Civil Aeronautics BoardLupon ng Aeronautika SibilLogo of Civil Aeronautics Board of the PhilippinesAgency overviewFormedDecember 5, 1932; 90 years ago (1932-12-05)HeadquartersOld MIA Road, Pasay, Metro ManilaAnnual budget₱203.87 million (2021)[1]Agency executivesCarmelo L. Arcilla, Executive DirectorPorvenir P. Porciuncula, Deputy Executive DirectorParent agencyDepartment of TransportationWebsitewww.cab.gov.ph The Civil Aeronautics Board (Filipino: Lupon ng Aeronau...

Gurdwara in Wan Chai District, Hong KongKhalsa Diwan Sikh Gurudwaraخالسا دیوان سکھّ گرودواراਖਾਲਸਾ ਦੀਵਾਨ ਸਿੱਖ ਗੁਰੂਦਵਾਰਾAlternative namesGurdwaraGeneral informationTypeGurdwaraLocationWan Chai DistrictAddress371 Queen's Road East, Wan Chai, Hong KongCountryHong KongEstimated completion1901Opened1901Inaugurated1901Renovated1930s1980s2018-2022CostHK$170,000,000Renovation costNo rent requiredClientSikh Community and Sindhi Communi...

José Carlos Fernández kan verwijzen naar: José Carlos Fernández (Peruviaanse voetballer) (1983), Peruviaans voetballer José Carlos Fernández (Spaanse voetballer) (1987), Spaans voetballer José Carlos Fernández (Boliviaans voetballer) (1971), Boliviaans voetballer Bekijk alle artikelen waarvan de titel begint met José Carlos Fernández of met José Carlos Fernández in de titel. Dit is een doorverwijspagina, bedoeld om de verschillen in betekenis of gebruik va...

European Network for Training in Economic ResearchAbbreviationENTERFormation1990TypeNGOLocationMannheim, Baden-Württemberg, GermanyMembership Universitat Autonoma de Barcelona Université Libre de Bruxelles Universidad Carlos III de Madrid University of Mannheim University of Stockholm Université Toulouse 1 Capitole Tilburg University University College London Stockholm School of EconomicsWebsiteenter-network.org The European Network for Training in Economic Research (ENTER) is an exchange ...

Discontinued US-based general encyclopedia The encyclopedia in a German library, 2011 Collier's Encyclopedia is a discontinued general encyclopedia first published in 1949 by P. F. Collier and Son in the United States.[1][2] With Encyclopedia Americana and Encyclopædia Britannica, Collier's Encyclopedia became one of the three major English-language general encyclopedias. The three were sometimes collectively called the ABCs.[3] In 1998, Microsoft acquired the right t...
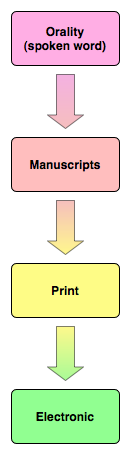
Culture depending on hand-written manuscripts The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (May 2022) (Learn how and when to remove this template message) The transition of communication technology: oral culture, manuscript culture, print culture, and Information Age A manuscript culture is a culture that depends on hand-written manuscri...

Leading member of the Dominican Order BlessedRaymond of CapuaO.P.PriestBornca. 1303[1]Capua, Kingdom of NaplesDied5 October 1399 (aged 96)Nuremberg, Holy Roman EmpireVenerated inRoman Catholic ChurchBeatified15 May 1899, Saint Peter's Basilica, Kingdom of Italy by Pope Leo XIIIMajor shrineChurch of San Domenico Maggiore, Naples, ItalyFeast5 OctoberAttributesDominican habit Legenda maior sanctae Catharinae Senensis, 1477 La vita di Santa Caterina da Siena (Legenda maior), 1707 Ray...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) جيرالد ستانلي لي معلومات شخصية الميلاد 4 أكتوبر 1862[1][2] بروكتون[3][1][2] الوفاة 3 أبريل 1944 (81 سنة) [3][1][4] نورثهامبتون...

















![{\displaystyle X\sim \operatorname {NEF} [\mu ,V(\mu )].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ce52184c075fd5c506eaef7a99a0c7fac4a2322)
![{\displaystyle \operatorname {E} [X]=\nabla A({\boldsymbol {\theta }}){\text{ and }}\operatorname {Cov} [X]=\nabla \nabla ^{\rm {T}}A({\boldsymbol {\theta }})\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2acafb1ec6cd50a88bc14d204496fcfbc2b48e7c)































