Poisson binomial distribution
| |||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Lukáš Rosol Lukáš RosolPaís República Checa República ChecaResidencia Praga, República ChecaFecha de nacimiento 24 de julio de 1985 (38 años)Lugar de nacimiento Brno, ChecoslovaquiaAltura 1,93 m (6′ 4″)Peso 83 kg (183 lb)Entrenador Jaroslav LevinskýProfesional desde 2004Brazo hábil Diestro (Revés a dos manos)Dinero ganado 4 493 341 dólares estadounidensesPerfil oficial Perfil IndividualesRécord de su carrera 121–153Títulos de su carrera 2 ATP...

Turkish state institution for religious affairs Diyanet redirects here. For other uses, see Diyanet (disambiguation). Directorate of Religious AffairsLogo of the Directorate of Religious AffairsFormation3 March 1924TypeIslamic education, religious administrationHeadquartersAnkara, TurkeyLocationÇankaya, Ankara, TurkeyOfficial language TurkishPresidentAli ErbaşBudget $2 billion (2020)[1]WebsiteOfficial website Document given by the Presidency of Religious Affairs for the mosque built...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: He Knew He Was Right TV serial – news · newspapers · books · scholar · JSTOR (March 2020) (Learn how and when to remove this template message) British TV series or programme He Knew He Was RightGenreCostume dramaWritten byAndrew DaviesDirected byTom VaughanStarringGeoffrey PalmerBill NighyCompose...

Eingang Nordseite des Law Quadrangles University of Michigan Law Library Die University of Michigan Law School ist Teil der University of Michigan in Ann Arbor, Michigan, USA. Inhaltsverzeichnis 1 Akademisches Profil 2 Architektonische Bedeutung 3 Affirmative-Action-Kontroverse 4 Einzelnachweise 5 Literatur 6 Weblinks Akademisches Profil Die Law School wurde 1859 gegründet und wird zurzeit von ca. 1.200 Studenten besucht. Der Großteil der Studierenden strebt den amerikanischen Abschluss Jur...

Fortnum & MasonJenisAnak perusahaanIndustriRitelDidirikan1707; 315 tahun lalu (1707)PendiriWilliam FortnumHugh MasonKantorpusatPiccadilly no. 181London, W1Britania RayaCabang5 (2019)[1]Wilayah operasiBritania RayaHong KongSeluruh dunia (via distributor dan daring)TokohkunciChairman: Kate Hobhouse CEO: Ewan VentersProdukBarang mewahKaryawan708 (2016) [2]IndukWittington Investments LtdSitus webfortnumandmason.com Fortnum & Mason (biasa disebut Fortnum's) adalah sebu...
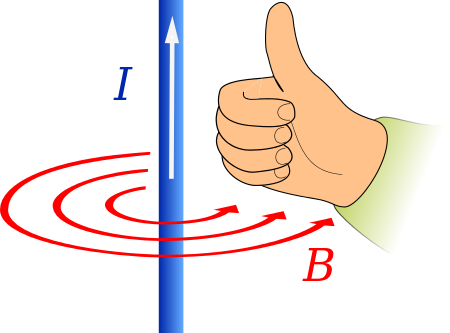
Untuk memahami kemiringan sumbu, anggaplah solenoid biru dalam aturan genggam tangan kanan ini sebagai sumbu rotasi Bumi, arah medan magnet berlawanan arah jarum jam selaku 'bidang orbit' Bumi dan arah jempol mengarah ke kutub utara Bumi. Dalam figur ini, 'kemiringan sumbu' bernilai nol derajat karena sumbu rotasinya perpendikuler terhadap bidang orbit. Jika solenoid biru (sumbu rotasi) ini miring ketika bidang orbit masih tetap, maka peristiwa ini disebut kemiringan sumbu planet atau benda l...

Año 1837Años 1834 • 1835 • 1836 ← 1837 → 1838 • 1839 • 1840Decenios Años 1800 • Años 1810 • Años 1820 ← Años 1830 → Años 1840 • Años 1850 • Años 1860Siglos Siglo XVIII ← Siglo XIX → Siglo XXTabla anual del siglo XIX Ir al año actualCategorías Categoría principalNacimientos • Fallecimientos • Por país 1837 en otros calendariosCalendario gregoriano 1837MDCCCXXXVIIAb Urbe condita 2590Calendario armenio 1286Calendario chino 4533-453...

Direktorat Jenderal Amerika dan Eropa Kementerian Luar Negeri Republik IndonesiaSusunan organisasiDirektur JenderalI Gede Ngurah Swajaya[1]Sekretaris Direktorat JenderalOurina Ritonga [1] DirekturAmerika 1Iwan Freddy Hari Susanto [1]Amerika 2Darianto Harsono [1]Eropa 1R. Widya Sadnovic [1]Eropa 2Winardi Hanafy Lucky [1]Kerjasama Intra Kawasan Amerika dan EropaNidya Kartikasari [1] Kantor pusatJl. Pejambon No.6. Jakarta Pusat, 10110Situs&...

First-level administrative subdivisions of Somaliland Not to be confused with States and regions of Somalia. Regions of SomalilandGobollada Somaliland (Somali)محافظات صوماليلاند(Arabic)CategoryUnitary republicLocationRepublic of SomalilandCreated byConstitution of SomalilandNumber6Populations251,384 (Sahil) — 1,242,003 (Maroodi Jeex)(2014 estimates)Areas13,930 km2 (5,380 sq mi) (Sahil) –54,231 km2 (20,939 sq mi) (Sanaag)GovernmentRegiona...

Australian TV series or program Let Loose LiveTitle cardDirected byTed EmeryStarringPeter MoonMichael VeitchMarg DowneyColin LaneDave O'NeilJane HallAndrew CurryPaul CallejaQueenie van de ZandtKate McLennanSam McMillanJulie EckersleyCountry of originAustraliaNo. of episodes2ProductionRunning timeapprox 0:60(including commercials)Original releaseNetworkSeven NetworkRelease29 May (2005-05-29) –5 June 2005 (2005-06-05) Let Loose Live, premiering on Sunday 29 May 2005, was a...

2017 film MotorradFilm posterDirected byVicente AmorimWritten byVicente AmorimStory byL. G. Tubaldini JrProduced byL. G. Tubaldini JrStarringCarla SalleDistributed byWarner Bros. PicturesRelease dates 9 September 2017 (2017-09-09) (TIFF) 1 March 2018 (2018-03-01) (Brazil) CountryBrazilLanguagePortuguese Motorrad is a 2017 Brazilian thriller film directed by Vicente Amorim. It was screened in the Contemporary World Cinema section at the 2017 Toronto Intern...

Bruno Canino in concerto nel 2008 Bruno Canino (Napoli, 30 dicembre 1935) è un pianista, clavicembalista e compositore italiano. Indice 1 Biografia 2 Note 3 Bibliografia 4 Altri progetti Biografia Nasce a Napoli, nel quartiere Vomero. Il padre, ingegnere appassionato di musica e pianista dilettante, lo porta spesso al Teatro San Carlo ad ascoltare l’opera. Il giovanissimo Canino si appassiona ben presto al melodramma di Giacomo Puccini. In casa c’è un pianoforte e dopo un anno di studi ...

Lambang Filipina Lambang negara Filipina, menampilkan Matahari berjurai delapan berkas sinar khas Filipina yang masing-masing melambangkan delapan provinsi (Batangas, Bulacan, Cavite, Manila, Laguna, Nueva Ecija, Pampanga dan Tarlac) yang ditetapkan dalam hukum darurat dalam keadaan perang oleh Gubernur Jenderal Filipina Ramón Blanco ketika pecahnya Revolusi Filipina. Sedangkan tiga bintang emas bersudut lima melambangkan tiga kawasan utama Filipina yaitu Luzon, Visayas, dan Mindanao. Namun,...

1996 American filmJoe's ApartmentTheatrical release posterDirected byJohn PaysonWritten byJohn PaysonBased onJoe's Apartmentby John PaysonProduced by Diana Phillips Bonni Lee Starring Jerry O'Connell Megan Ward CinematographyPeter DemingEdited byPeter FrankMusic byCarter BurwellProductioncompanies The Geffen Film Company MTV Productions Distributed byWarner Bros.Release date July 26, 1996 (1996-07-26) Running time80 minutesCountryUnited StatesLanguageEnglishBudget$13 millionBox...

Indian academic This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: Excessive detail information. Please help improve this article if you can. (April 2014) (Learn how and when to remove this template message) This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See...

Private Chinese-Filipino school This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Philippine Cultural College – news · newspapers · books · scholar · JSTOR (March 2014) (Learn how and when to remove this template message) Philippine Cultural College菲律濱僑中學院Former namesPhilippine Chinese High Schoo...

Erica discolor Klasifikasi ilmiah Kerajaan: Plantae Divisi: Tracheophyta Kelas: Magnoliopsida Ordo: Ericales Famili: Ericaceae Genus: Erica Spesies: Erica discolor Nama binomial Erica discolorAndrews Erica discolor adalah spesies tumbuhan yang tergolong ke dalam famili Ericaceae. Spesies ini juga merupakan bagian dari ordo Ericales. Spesies Erica discolor sendiri merupakan bagian dari genus Erica.[1] Nama ilmiah dari spesies ini pertama kali diterbitkan oleh Andrews. Referensi ^ Erica...

بوابة الإمبراطورية الألمانية أرشيف صورة مختارة طالع صفحة التصنيفات طالع صفحة الأرشيف طالع صفحة البناء طالع صفحة البوابات حدّث محتوى الصفحة البوابة صور قصر شتولسنفلس البرج العالي جسر بالدوين قصر الأمراء الناخبين رايشسبورج كوخم مقالة جمعية القيصر فيلهلم لتقدم العلوم حرك�...

ميّز عن محمد إبراهيم القزويني. إبراهيم القزويني إبراهيم بن محمّد باقر الموسوي القزويني معلومات شخصية الميلاد سنة 1799 قزوين الوفاة 15 سبتمبر 1848 (48–49 سنة) كربلاء، وإيالة بغداد سبب الوفاة كوليرا مواطنة السلالة القاجاريةمماليك العراقالعراق تحت الح�...

Former currency of the Ottoman Empire, Turkey, Egypt, Montenegro, Albania and Yugoslavia 50 para of 1965 The para (Ottoman Turkish: پاره, romanized: pare, para, from Persian پاره, pâre, 'piece';[1][2] Cyrillic: пара) was a former currency of the Ottoman Empire, Turkey, Egypt, Montenegro, Albania and Yugoslavia and is the current subunit, although rarely used, of the Serbian dinar. In 1524, the Ottoman law code of Egypt (kanunname) referred to the Mamluk Egypt...
![{\displaystyle \mathbf {p} \in [0,1]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5233cb53cf328b3491ef7536c5b52e63e6c854a2)






























![{\displaystyle P_{i}=[1-p_{i},p_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3518ad3a5cf4ceecdc7a85100aa2cacdbee8877)

















![{\displaystyle {\begin{aligned}\Pr[S\geq s]&\leq \exp(-st)\operatorname {E} \left[\exp \left[t\sum _{i}X_{i}\right]\right]\\&=\exp(-st)\prod _{i}(1-p_{i}+e^{t}p_{i})\\&=\exp \left(-st+\sum _{i}\log \left(p_{i}(e^{t}-1)+1\right)\right)\\&\leq \exp \left(-st+\sum _{i}\log \left(\exp(p_{i}(e^{t}-1))\right)\right)\\&=\exp \left(-st+\sum _{i}p_{i}(e^{t}-1)\right)\\&=\exp \left(s-\mu -s\log {\frac {s}{\mu }}\right),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/426dec4ba9249bf33ce22f36c2b5735fb5cba7e5)




















