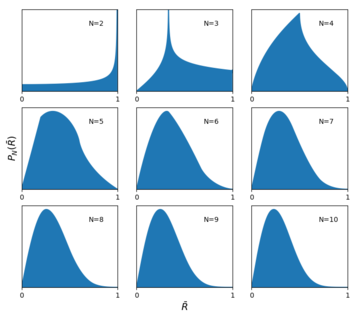
Circular uniform distribution
|
Read other articles:

American football player (born 1989) American football player Devin TaylorTaylor in 2014No. 92, 97, 98Position:Defensive endPersonal informationBorn: (1989-11-15) November 15, 1989 (age 34)Lady's Island, South Carolina, U.S.Height:6 ft 7 in (2.01 m)Weight:266 lb (121 kg)Career informationHigh school:Beaufort(Beaufort, South Carolina)College:South CarolinaNFL Draft:2013 / Round: 4 / Pick: 132Career history Detroit Lions (2013–2016) New York G...
Опис файлу Опис постер фільму «Грізні ночі» Джерело https://www.kino-teatr.ru/kino/movie/sov/15997/annot/ Час створення 1960 Автор зображення Ялтинська кіностудія Ліцензія див. нижче Обґрунтування добропорядного використання Обґрунтування добропорядного використання не вказано назву статт�...

小田急ロマンスカー > えのしま (列車) この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: えのしま 列車 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2012年5...

Cet article est une ébauche concernant les transports en commun et Kiev. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Tramway de Kiev (uk) Київський трамвай Situation Kiev Ukraine Type Tramway Entrée en service 1891 (traction hippomobile)1892 (traction vapeur)1892 (traction électrique)1979 (tramway rapide) Fin de service 1896 (traction hippomobile)1904 (traction vapeur) Longueur du réseau 1...

María Rosa Gallo Fotografía de María Rosa Gallo en 1956.Información personalNacimiento 20 de diciembre de 1921 Buenos Aires (Argentina) Fallecimiento 7 de diciembre de 2004 (82 años)Buenos Aires (Argentina) Causa de muerte Neumonía Sepultura Cementerio de la Chacarita Nacionalidad ArgentinaFamiliaCónyuge Tito AlonsoCamilo Da Passano Hijos Claudio da PassanoAlejandra da Passano Información profesionalOcupación Actriz Área Actuación Años activa 1943-2004Distinciones Premio Konex de ...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (février 2023). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Cet article est une ébauche concernant le droit français. Vous pouvez partager vos connaissan...

1884 treaty between the United Kingdom and Transvaal London Convention (1884)A Convention Between Her Majesty the Queen of the United Kingdom of Great Britain and Ireland and the South African RepublicDelegates from the South African Republic to the London Convention (1884).TypeRetrocession AgreementContextRetrocession of the South African Republic after the First Boer WarSigned27 February 1884LocationLondonEffective27 February 1884ConditionRatification by four signatoriesExpiration31 May 190...

This article is about the Region, the first-level administrative unit of Namibia. For the electoral constituency, see Ohangwena Constituency. For the suburb and former village of Ohangwena, see Helao Nafidi. Region in NamibiaOhangwena RegionRegionLocation of the Ohangwena Region in NamibiaCountryNamibiaCapitalEenhanaGovernment • GovernorSebastian Ndeitunga[1]Area[2] • Total10,706 km2 (4,134 sq mi)Population (2011)[3] •...

2008 French comedy film by Dany Boon This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Welcome to the Sticks – news · newspapers · books · scholar · JSTOR (October 2017) (Learn how and when to remove this template message) Welcome to the SticksFilm posterDirected byDany BoonWritten by Dany Boon Alexandre Charl...

Cet article concerne l'ancienne résidence présidentielle ukrainienne. Pour la ville fermée russe, voir Mejgorié. Cet article est une ébauche concernant l’Ukraine. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Plan de localisation de Mejyhiria. Mejyhiria (en ukrainien : Межигір'я, aussi en français Mejiguiria, Mezhyhirya, Mezhihiria) ou Mejgorié[1], ce qui signifie « entre les col...

Hip hop disc jockey discography DJ Drama discographyDJ Drama In 2008Studio albums6Music videos10Singles6 This is the discography of American hip-hop artist DJ Drama. His first album, Gangsta Grillz: The Album, was released in December 2007. It contained two singles: 5000 Ones, featuring Nelly, T.I., Yung Joc, Willie the Kid, Young Jeezy, Diddy and Twista, and The Art of Storytellin' Part 4, featuring OutKast and Marsha Ambrosius. His second album was released two years later. On Gangsta Grill...

Скомороський провулокКиїв Кінцева (збережена) частина Скомороського провулкуМісцевість Арештантські городи, ЄвбазРайон Шевченківський(на той час — Радянський)Колишні назви Дяківський пров.Загальні відомостіКоординати початку 50°26′49″ пн. ш. 30°29′22″ сх. д.&#x...

Carl Peter ThunbergLahir(1743-11-11)11 November 1743Jönköping, SwediaMeninggal8 Agustus 1828(1828-08-08) (umur 84)Thunaberg, Uppland, SwediaKebangsaanSwediaNama lainCarl Pehr ThunbergCarl Per ThunbergThunb.PekerjaanNaturalis Carl Peter Thunberg, yang juga dikenal sebagai Karl Peter von Thunberg, Carl Pehr Thunberg, atau Carl Per Thunberg (11 November 1743 – 8 Agustus 1828), adalah seorang naturalis Swedia dan seorang murid dari Carl Linnaeus. Ia disebut bapak botani Afrika Selat...

Fictional character in the 2016 video game Overwatch Fictional character ZaryaOverwatch characterZarya's appearance in Overwatch.First gameOverwatch (2016)Created byGeoff Goodman[1]Designed byArnold Tsang[2]Voiced byDolya Gavanski[3]In-universe informationClassTankOriginSiberia, RussiaNationalityRussian Zarya, full name Aleksandra Zaryanova, is an Overwatch character who first appears in the 2016 video game of the same name, a Blizzard Entertainment–developed first-p...

Horse racing track in Melbourne, Victoria, Australia This article is about the racecourse in Australia. For the racecourse in the United Kingdom, see Sandown Park Racecourse. Ladbrokes Park formerly known as Sandown RacecourseSandown Racecourse finish postLocationMelbourne, VictoriaDate opened19 June 1965Screened onSeven Network Sandown Racecourse (also known as Ladbrokes Park due to naming rights)[1] is a Thoroughbred horse racing race track administered by the Melbourne Racing Club ...

Shopping mall in Alabama, United StatesGadsden MallLocationGadsden, Alabama, United StatesCoordinates33°59′44.12″N 86°0′26″W / 33.9955889°N 86.00722°W / 33.9955889; -86.00722Opening dateJuly 31, 1974[1]DeveloperColonial Properties[1]ManagementKohan Retail Investment GroupOwnerKohan Retail Investment GroupNo. of stores and services70+No. of anchor tenants3 (1 open, 2 vacant)Total retail floor area502,591 square feet (46,692.2 m2)[2&#...

American politician and businessman (born 1947) This article is about the American politician. For the football player who went by the same name, see Milton Romney. For the singer with a similar sounding name, see Ritt Momney. Mitt RomneyOfficial portrait, 2019United States Senatorfrom UtahIncumbentAssumed office January 3, 2019Serving with Mike LeePreceded byOrrin Hatch70th Governor of MassachusettsIn officeJanuary 2, 2003 – January 4, 2007LieutenantKerry HealeyPre...

21°29′2″N 39°11′16″E / 21.48389°N 39.18778°E / 21.48389; 39.18778 بيت نصيفبيت نصيفمعلومات عامةنوع المبنى بيتالمكان جدة، منطقة مكة المكرمةالبلد السعوديةمعلومات أخرىالإحداثيات 21°29′02″N 39°11′16″E / 21.4839°N 39.1878°E / 21.4839; 39.1878 تعديل - تعديل مصدري - تعديل ويكي بيانات بيت نصيف�...

Fort Columbia State ParkHistoric wood-frame buildings at Fort Columbia State ParkLocation in the state of WashingtonShow map of Washington (state)Fort Columbia State Park (the United States)Show map of the United StatesLocationPacific County, Washington, United StatesCoordinates46°15′36″N 123°55′08″W / 46.26000°N 123.91889°W / 46.26000; -123.91889[1]Area618 acres (250 ha)Elevation709 ft (216 m)[1]Established1950OperatorWashing...

American professional organization American Institute for ConservationAmerican Institute for Conservation (AIC)Founded1972; 51 years ago (1972)AffiliationsProfessional associationWebsitewww.culturalheritage.org The American Institute for Conservation (AIC) is a national membership organization of conservation professionals, headquartered in Washington, D.C. History The AIC first launched in 1972 with only a handful of members. Now it is grown to over 3,500 members in over tw...