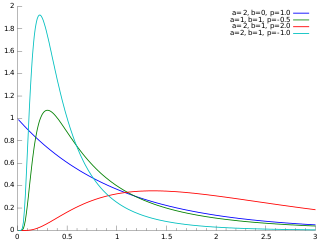
Generalized inverse Gaussian distribution
| |||||||||||||||||||||||||||||||||||||
Read other articles:

Playa Ramírez Playa Ramírez en 2011.UbicaciónPaís UruguayUbicación Montevideo, UruguayCoordenadas 34°54′58″S 56°10′13″O / -34.9162, -56.17018Características específicasComposición Arena doradaCondiciones baño Oleaje calmoSeguridadSalvamento SíAccesibilidadTipo de acceso fácil a pie, ómnibus[editar datos en Wikidata] La playa Ramírez es una playa en Montevideo, Uruguay. Está situada en el Río de la Plata, en la Rambla Pres...

Броненосець «Кайзер Макс» Історія Австро-Угорщина Назва: SMS Kaiser MaxБудівник: «Stabilimento Tecnico Triestino», ТрієстЗакладений: жовтень 1861 рокуПрийнятий: 1863 рікВиведений: Перебудований у 1873-1876 роках Основні характеристики Тип: Броненосець однойменного типуВодотоннажність: 3 588 т (с�...

Cantata by Alexander Glazunov Commemorative Cantata for the Centenary of the Birth of Pushkinby Alexander GlazunovThe composer in 1899Opus65OccasionCentenary of Alexander PushkinTextKonstantin RomanovLanguageRussianPerformed1899 (1899)Movements5Scoring Mezzo-soprano Tenor SATB choir Piano External imagesOriginal text of the cantata Page 1 Page 2 Page 3 Commemorative Cantata for the Centenary of the Birth of Pushkin (Russian: Торжественная кантата в память 100-�...

Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Goldene Rose (Begriffsklärung) aufgeführt. Goldene Rose von Giuseppe und Pietro Paolo Spagna. Rom, um 1818/19 in der Wiener Schatzkammer Die Goldene Rose (auch Papstrose, Tugendrose; lateinisch Rosa aurea) ist eine päpstliche Auszeichnung. Die Rose ist ein aus vergoldetem Silber geschmiedeter Rosenstrauß aus sechs Rosenzweigen mit sechs Blüten, die mit wohlriechenden Essenzen (Balsame und Moschus) gefüllt sind. Das...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها...

آه بيكو (بالإنجليزية: Ah Peku) إله الرعد في الديانة المايانية في أمريكا الوسطى، وهو يعيش فوق قمم الجبال ويصعد إلى السحب قبل أن تمطر.[1][2] انظر أيضًا أبوري (ميثولوجيا) أبا (أساطير هندية) بيغ فوت أكاسيلا (ميثولوجيا) آه كانكوم آه كين اكسوك آه كوميكس يونيكوب آه هولنب آه كين ا�...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) بلاس س. سيلفا باوتشر معلومات شخصية الميلاد 2 فبراير 1869 الوفاة 27 يناير 1949 (79 سنة) بونس، بورتوريكو مواطنة الولايات المتحدة الحياة العملية المه�...

A dial constructed using Waugh's schema Vertical declining dials are sundials that indicate local apparent time. Vertical south dials are a special case: as are vertical north, vertical east and vertical west dials. The word declining means that the wall is offset from one of these 4 cardinal points. There are dials that are not vertical, and these are called reclining dials.[1] A sundial schema uses a compass and a straight edge to firstly derive the essential angles for that latitud...

City nicknames Philadelphia skyline as seen from Belmont Plateau, in Fairmount Park Philadelphia has long been nicknamed The City of Brotherly Love from the literal meaning of the city's name in Greek (Greek: Φιλαδέλφεια ([pʰilaˈdelpʰeːa], Greek pronunciation: [filaˈðelfia]), brotherly love), derived from the Ancient Greek terms φίλος phílos (beloved, dear, or loving) and ἀδελφός adelphós (brother, brotherly).[1] The city was first named...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) بيدرو بيزارو معلومات شخصية الميلاد سنة 1515 طليطلة الوفاة العقد 1570 أريكيبا مواطنة إسبانيا الحياة العملية المهنة مستكشف، وكاتب اللغات ا...

You can help expand this article with text translated from the corresponding article in French. (December 2011) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikip...

2023 studio album by FeidMor, No Le Temas a la OscuridadStudio album by FeidReleased29 September 2023GenreReggaetonLength45:06LanguageSpanishLabelUniversal LatinoProducerSky RompiendoWainJowanTaikoIconFeidCashMoneyAPDaniel MorasWizzleRoloCupidoFeid chronology Sixdo(2022) Mor, No Le Temas a la Oscuridad(2023) Singles from Mor, No Le Temas a la Oscuridad Niña BonitaReleased: 21 April 2023 Vente ConmigoReleased: 4 August 2023 Ferxxo 151Released: 25 August 2023 BubalúReleased: 22 Septem...

بطولة ويمبلدون 1981 جزء من بطولة ويمبلدون رقم الفعالية 95 البلد المملكة المتحدة التاريخ 1981 الرياضة كرة المضرب الفعاليات بطولة ويمبلدون 1981 - فردي السيدات، وبطولة ويمبلدون 1981 - فردي الرجال، وبطولة ويمبلدون 1981 - زوجي السيدات، وبطولة ويمبلدون 1981 - زوجي ا�...

Former Royal castle in Beeston, Cheshire, England Beeston CastlePart of CheshireBeeston, England A modern bridge provides access to the gateway of the inner ward. Location map and quick summary Beeston CastleCoordinates53°07′40″N 2°41′29″W / 53.1277°N 2.6913°W / 53.1277; -2.6913TypeEnclosure castleHeight9 metres (30 ft)Site informationOwnerEnglish HeritageConditionRuinSite historyBuiltc. 1220Built byRanulf de BlondevilleIn useOpen to publicMa...

For the island, see Moose Factory Island. Place in Ontario, CanadaMoose FactorySt. Thomas' Anglican ChurchNickname: Moose AntlersMoose FactoryCoordinates: 51°15′20″N 80°36′18″W / 51.25556°N 80.60500°W / 51.25556; -80.60500[1]CountryCanadaProvinceOntarioRegionNortheastern OntarioDistrictCochraneSettled1673Renamed1686Government • Typemultiple governments • Federal ridingTimmins—James Bay • Prov. ridingMushkeg...

نيشان النجم القطبي مؤسس منغوليا البلد منغوليا يُمنح من طرف منغوليا سميت باسم الجدي إحصاءات تاريخ الإنشاء 1936 العدد الممنوح 30.000 صورة شريط الوسام تعديل مصدري - تعديل نيشان النجم القطبي (بالمنغولية: Алтан гадас одон Altan Gadas Odon) هو أعلى نيشان مدني يمكن أن تمن�...

胸腺喷丁臨床資料其他名稱(3S)-3-[[(2S)-6-amino-2-[[(2S)-2-amino-5-(diaminomethylideneamino)pentanoyl]amino]hexanoyl]amino]-4-[[(2S)-1-[[(2S)-1-hydroxy-3-(4-hydroxyphenyl)-1-oxopropan-2-yl]amino]-3-methyl-1-oxobutan-2-yl]amino]-4-oxobutanoic acidATC碼L03AX09 (WHO) 识别信息 IUPAC命名法 L-arginyl-L-lysyl-L-α-aspartyl-L-valyl-L-tyrosine CAS号69558-55-0 YPubChem CID451417ChemSpider397640 YUNIIO3Y80ZF13FKEGGD06117 YChEMB...

American musician This biography of a living person relies too much on references to primary sources. Please help by adding secondary or tertiary sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately, especially if potentially libelous or harmful.Find sources: Yppah – news · newspapers · books · scholar · JSTOR (February 2009) (Learn how and when to remove this template message) YppahBirth na...

عبدالله الحمدان معلومات شخصية الاسم الكامل عبدالله عبدالرحمن الحمدان الميلاد 13 سبتمبر 1999 (العمر 24 سنة)الرياض، المملكة العربية السعودية الطول 1.83 م (6 قدم 0 بوصة) مركز اللعب مهاجم الجنسية السعودية معلومات النادي النادي الحالي الهلال الرقم 14 مسيرة الشباب سنوات فري...

الكونتيسه حافية القدمين (بالانجليزى: The Barefoot Contessa) الصنف فيلم رومانسى، وفيلم دراما تاريخ الصدور 1954 مدة العرض البلد امريكا ايطاليا اللغه الاصليه انجليزى الطاقم المخرج جوزيف مانكيفيتس الإنتاج جوزيف مانكيفيتس، وانجيلو ريزولى سيناريو جوزيف �...

![{\displaystyle \operatorname {E} [x]={\frac {{\sqrt {b}}\ K_{p+1}({\sqrt {ab}})}{{\sqrt {a}}\ K_{p}({\sqrt {ab}})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9eea374ea6d263f4dec6f737248ac6c7ee9edec4)
![{\displaystyle \operatorname {E} [x^{-1}]={\frac {{\sqrt {a}}\ K_{p+1}({\sqrt {ab}})}{{\sqrt {b}}\ K_{p}({\sqrt {ab}})}}-{\frac {2p}{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b8243064fe20b0eb33317bf58d29ad616bbd2ff)
![{\displaystyle \operatorname {E} [\ln x]=\ln {\frac {\sqrt {b}}{\sqrt {a}}}+{\frac {\partial }{\partial p}}\ln K_{p}({\sqrt {ab}})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f49d3a11593033dcb22f9bf4f12377957b4ecc5b)

![{\displaystyle \left({\frac {b}{a}}\right)\left[{\frac {K_{p+2}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}-\left({\frac {K_{p+1}({\sqrt {ab}})}{K_{p}({\sqrt {ab}})}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb650b320e436e5cc35f33ed94c0794e9f4c58ea)








![{\displaystyle {\begin{aligned}H={\frac {1}{2}}\log \left({\frac {b}{a}}\right)&{}+\log \left(2K_{p}\left({\sqrt {ab}}\right)\right)-(p-1){\frac {\left[{\frac {d}{d\nu }}K_{\nu }\left({\sqrt {ab}}\right)\right]_{\nu =p}}{K_{p}\left({\sqrt {ab}}\right)}}\\&{}+{\frac {\sqrt {ab}}{2K_{p}\left({\sqrt {ab}}\right)}}\left(K_{p+1}\left({\sqrt {ab}}\right)+K_{p-1}\left({\sqrt {ab}}\right)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d663373bdf483797c0ce4ada0238439389242a3)
![{\displaystyle \left[{\frac {d}{d\nu }}K_{\nu }\left({\sqrt {ab}}\right)\right]_{\nu =p}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3838a857c40b56dee47ed55dade77403f6657cb8)






![{\displaystyle f(x;\mu ,\lambda )=\left[{\frac {\lambda }{2\pi x^{3}}}\right]^{1/2}\exp {\left({\frac {-\lambda (x-\mu )^{2}}{2\mu ^{2}x}}\right)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/430c36a80c0f4de08f8b56fe7019d79e5d8aea68)




















