Limite (matematica)
|
Read other articles:

Old Cleveland RoadQueenslandOld Cleveland Road at CarinaGeneral informationTypeRoadLength19.3 km (12 mi)Route number(s) State Route 22 State Route 30 State Route 54 State Route 55 Major junctionsWest end Logan Road (State Route 95), GreenslopesEast end Old Cleveland Road East (State Route 55), BirkdaleLocation(s)Major suburbsCoorparoo, Camp Hill, Carina, Carindale, Chandler, Capalaba Old Cleveland Road is a major road in Brisbane, Queensland. It runs 19.3 kilometres (12.0 mi) f...

ヴァイマル、デッサウ及びベルナウのバウハウスとその関連遺産群(ドイツ) デッサウ・バウハウス英名 Bauhaus and its Sites in Weimar, Dessau and Bernau仏名 Bauhaus et ses sites à Weimar, Dessau et Bernau面積 8.1614 ha (緩衝地帯 59.26 ha)登録区分 文化遺産登録基準 (2), (4), (6)登録年 1996年拡張年 2017年公式サイト 世界遺産センター(英語)地図 使用方法・表示 ヴァイマル、デッサウ及びベ...

Tóm tắt một số cách pha etanol chính trên thế giới Có một số hỗn hợp nhiên liệu etanol phổ biến được sử dụng trên thế giới. Việc sử dụng hoàn toàn ethanol lỏng hoặc khan trong động cơ đốt trong (ICE) chỉ khả thi nếu động cơ được thiết kế hoặc cho mục đích này, và chỉ được sử dụng cho xe ô tô, xe tải nhẹ và xe máy. Etanol khan có thể được pha với xăng để sử dụng trong đ�...

قرية بيت البوص الزكرية - قرية - تقسيم إداري البلد اليمن المحافظة محافظة صنعاء المديرية مديرية الحيمة الداخلية العزلة عزلة بني الحذيفي السكان التعداد السكاني 2004 السكان 183 • الذكور 95 • الإناث 88 • عدد الأسر 29 • عدد المساكن 29 معلومات أخرى التوقيت...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2021) فيكتور كريستالدو معلومات شخصية الميلاد 10 مايو 1967 (العمر 56 سنة)الأرجنتين مركز اللعب وسط الجنسية باراغواي معلومات النادي النادي الحالي -- مسيرة الشباب �...

الجمعية العربية السعودية للثقافة والفنون البلد السعودية المقر الرئيسي المقر الرئيس مدينة الرياض السعودية تاريخ التأسيس 1973 م النوع حكومية منطقة الخدمة 16 فرع في المملكة العربية السعودية العضوية وزارة الإعلام الموقع الرسمي http://www.sasca.org.sa/ تعديل مصدري - تعديل ال�...

Pemilihan Umum Bupati Maros 2020201520249 Desember 2020Terdaftar253.586 jiwaKehadiran pemilih197.104 (77,73 %)Kandidat Calon Andi Syafril Chaidir Syam Andi Harmil Mattotorang Andi Tajerimin Nur Partai PAN NasDem Independen Aliansi MAROS KEREN(PAN, Hanura, PBB, PPP) MAROS UNGGUL(NasDem, PKS) MAROS UNTUK SEMUA(Golkar, PKB, Demokrat, Gerindra) Pendamping Suhartina Bohari Andi Ilham Nadjamuddin Havid S. Fasha Suara rakyat 82.770 64.512 48.308 Persentase 42,32 % 32,98 % ...

January 2015 Greek legislative election ← June 2012 25 January 2015 September 2015 → All 300 seats in the Hellenic Parliament151 seats needed for a majorityOpinion pollsRegistered9,949,684Turnout63.62% (1.13pp) First party Second party Third party XA Leader Alexis Tsipras Antonis Samaras Nikolaos Michaloliakos Party Syriza ND ΧΑ Last election 26.89%, 71 seats 29.66%, 129 seats 6.92%, 18 seats Seats won 149 76 17 Seat change 78 53 1 Pop...

Subgenre of the action film genre For other uses, see Swashbuckler (disambiguation). Douglas Fairbanks as Robin Hood, 1922 Swashbuckler films are a subgenre of the action film genre, characterised by swordfighting and adventurous heroic characters, known as swashbucklers. While morality is typically clear-cut, heroes and villains alike often follow a code of honour. Some swashbuckler films have romantic elements, most frequently a damsel in distress. Both real and fictional historical events ...

2022 South Korean web series Rose MansionPromotional posterAlso known asThe MansionGenreThrillerSuspenseMysteryCrimeDeveloped byTVING[1]Written byYoo Kab-yeol[1]Directed byChang[1]Music byWoo-jooCountry of originSouth KoreaOriginal languageKoreanNo. of episodes12ProductionProduction companiesSLL[2]B.A. Entertainment[2]Film Monster[2]Original releaseNetworkTVINGReleaseMay 13 (2022-05-13) –May 27, 2022 (2022-05-27) Rose Mansion (K...

Species of flowering plant Rosy garlic Inflorescence of Allium roseum, blooming in Brest, France Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Monocots Order: Asparagales Family: Amaryllidaceae Subfamily: Allioideae Genus: Allium Subgenus: A. subg. Amerallium Species: A. roseum Binomial name Allium roseumL. 1753 not Krock. 1787[1] Synonyms[2] Molium roseum (L.) Fourr. Nectaroscordum roseum (L.) Galasso & Banfi Allium roseum,...

Brazilian publisher Editora GloboFormerlyRGE(1952-1986)Editora Globo Gaúcha(1986-2007)Infoglobo(1925-2017)TypeSubsidiaryIndustryPublishingGenreVariousFounded1986FounderRoberto MarinhoHeadquartersSão Paulo, SPNumber of locationsSão PauloRio de JaneiroBrasíliaKey peopleFrederic Kachar,CEOProductsBooks, magazines and newspapersOwnerGrupo GloboSubsidiariesGlobo LivrosInfogloboEdições Globo Condé Nast (70%)GlobosimWebsiteeditoraglobo.globo.com Editora Globo S.A. (Globo Editors) is a Brazili...

1903 French film by Georges Méliès The Damnation of FaustFinal scene of the film, with Mephisto jumping out of the floor and deploying his wings.Directed byGeorges MélièsStarringGeorges MélièsRelease date December 1903 (1903-12) Running time6 minutesCountryFranceLanguageSilent Faust aux enfers, released in the United States as The Damnation of Faust and in Britain as The Condemnation of Faust, is a 1903 French short silent film directed by Georges Méliès.[1] Producti...

東山 彰良(ひがしやま あきら) 東山彰良(左)と中華民国総統蔡英文、2016年6月17日誕生 王 震緒 (1968-09-11) 1968年9月11日(55歳) 台湾・台北市職業 小説家推理作家最終学歴 西南学院大学大学院経済学研究科活動期間 2002年 -ジャンル 推理小説・ハードボイルド小説・アクション小説代表作 『流』(2015年)『罪の終わり』(2016年)『僕が殺した人と僕を殺した人』(2017...

American college basketball season 2016–17 Miami RedHawks men's basketballConferenceMid-American ConferenceDivisionEast DivisionRecord11–21 (4–14 MAC)Head coachJohn Cooper (5th season)Assistant coaches Rick Duckett Sheldon Everett Trey Meyer Home arenaMillett HallSeasons← 2015–162017–18 → 2016–17 Mid-American Conference men's basketball standings vte Conf Overall Team W L PCT W L PCT East Akron 14 – 4 .778 27...

Red Blooded Woman Сингл Кайли Миноугс альбома Body Language Сторона «Б» «Almost a Lover»«Cruise Control»«Slow» (remix) Дата выпуска 1 марта 2004 Формат 12-дюймовый сингл (англ.) (рус., CD-сингл, макси-сингл (англ.) (рус. Дата записи 2003 Место записи El Cortijo Studios(Малага, Испания) Жанры Хип-хоп, синти-п�...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (December 2014) The topic of this article may not meet Wikipedia's notability guidelines for products and services. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be sh...
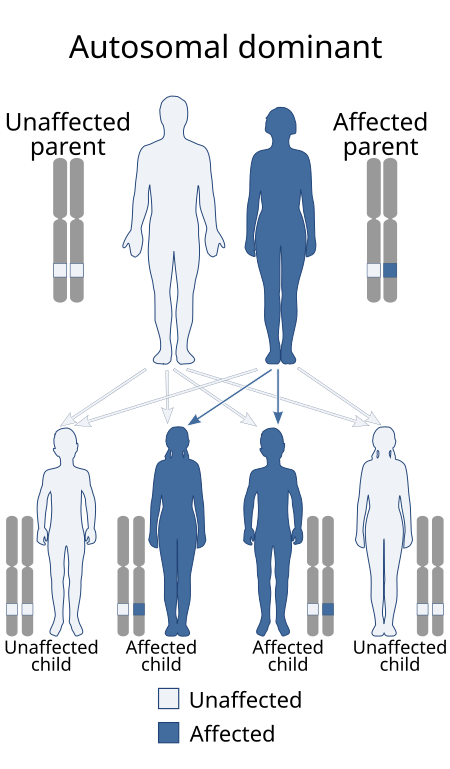
Rare neuromuscular disorder of infants characterised by severe progressive muscle atrophy Medical conditionSpinal muscular atrophy with lower extremity predominance 1Other namesLower extremity predominant spinal muscular atrophy type 1, SMALED1Spinal muscular atrophy with lower extremity predominance is inherited in an autosomal dominant manner.SpecialtyNeurologySymptomsProgressive muscle atrophy in legsUsual onsetInfancyCausesMutation in DYNC1H1 geneDiagnostic methodMolecular test Spinal mus...
Circassian tribe Not to be confused with Abkhazians.Part of a series on theCircassiansАдыгэхэр Circassia Adyghe Xabze Circassians List of notable CircassiansCircassian genocide Circassian diaspora Turkey Jordan Israel Syria Germany United States Saudi Arabia Libya Iraq Iran Egypt Bulgaria (historical) Kosovo (historical) Romania (historical) Circassian tribes Surviving Abadzekh Besleney Bzhedug Chemirgoy Hatuqway Kabardian Natukhaj Shapsug Ubykh Destroyed or barely existing Ademey Che...

American politician from Texas Caroline HarrisMember of the Texas House of Representativesfrom the 52nd districtIncumbentAssumed office 2022Preceded byJames Talarico Personal detailsBornRound Rock, Texas, U.S.Political partyRepublican Caroline Harris (born 1993 or 1994) is a Republican member of the Texas House of Representatives from District 52, serving since 2023. She is the youngest Republican woman ever elected to the Texas State House.[1] Education and career She...
















































