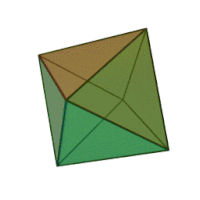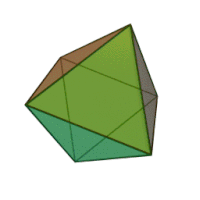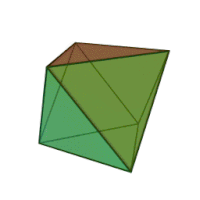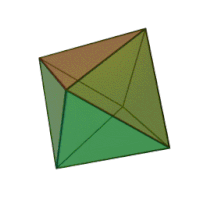
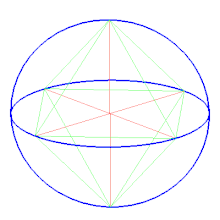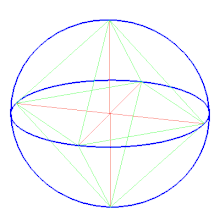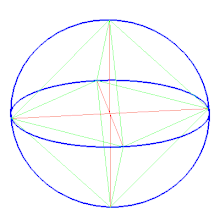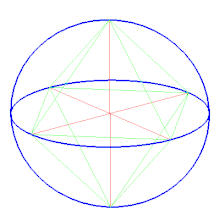
Октаедр
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Frontlines in 1918-1919 This article is about Russian civil War. For World War II, see Northern Front (Soviet Union). The Northern Front (Russian: Северный фронт) was a front of the Red Army during the Russian Civil War which was formed on 15 September 1918 to fight the troops of the interventionists and White Guards in the Northwest, North and Northeast of the Soviet Republic. The Northern Front covered the area between Pskov and Vyatka. It bordered the Eastern Front of the Red ...

This article is about Canadian television show. For Australian television show, see Prank Patrol (Australian TV series). For British television show, see Prank Patrol (British TV series). Canadian TV series or program Prank PatrolAndré Simoneau and the NinjasStarringAndré SimoneauCountry of originCanadaNo. of seasons4[1]No. of episodes100[1]ProductionRunning time25 minutesProduction companyApartment 11 ProductionsOriginal releaseNetworkYTVReleaseSeptember 6, 2005 (...

Kurt Weiler (* 16. August 1921 in Lehrte; † 2. August 2016 in Kleinmachnow) war einer der wichtigsten Trickfilmregisseure der DDR. Inhaltsverzeichnis 1 Leben 2 Filmografie (Auswahl) 3 Auszeichnungen 4 Weblinks 5 Einzelnachweise Leben Stolperstein am Wohnort Weilers in Lehrte vor dem Exil Grab auf dem Südwestkirchhof Stahnsdorf Weiler lebte von 1939 bis 1950 in England im Exil und begann sich in dieser Zeit mit dem künstlerischen Animationsfilm zu beschäftigen.[1] Er siedelte in d...

Frohnsdorf Gemeinde Nobitz Wappen von Frohnsdorf Koordinaten: 50° 56′ N, 12° 35′ O50.93583333333312.585833333333220Koordinaten: 50° 56′ 9″ N, 12° 35′ 9″ O Höhe: 220 m Fläche: 4,38 km² Einwohner: 244 (31. Dez. 2017) Bevölkerungsdichte: 56 Einwohner/km² Eingemeindung: 6. Juli 2018 Postleitzahl: 04603 Vorwahl: 034497 Karte Lage von Frohnsdorf in der Einheitsgemeinde Nobitz Frohnsdorf ist ein Ortsteil ...

「霹雳火 (电影)」重定向至此。關於同名的其它解釋,請見「霹靂火 (消歧義)」。 霹靂火Thunderbolt基本资料导演陳嘉上监制蔡瀾制片陳希文、羅秀慧编剧陳嘉上陳慶嘉郭偉鐘主演成龍袁詠儀楚原王敏德配乐梁邦彥摄影林國華劉鴻泉黃永恆關志勤陳廣鴻鄭兆強剪辑張耀宗張嘉輝吳宏雄陳祺合制片商嘉禾片长97分鐘产地 英屬香港语言粵語、英語、日語上映及发行上映日期 英屬

Teluk Laizhou (Cina disederhanakan: 莱州湾; tradisional Cina: 萊州灣; pinyin: LAIZHOU WAN) adalah teluk di bagian lengan selatan Laut Bohai (juga dikenal sebagai bagian Teluk Bohai), yang merupakan perpanjangan dari Teluk Korea (Northern Laut Kuning) di belakang Semenanjung Liaodong ke utara, dan Semenanjung Shandong di selatan. Kedua semenanjung kira-kira berbentuk segitiga dan menuju Selat Bohai, membuka keluar ke Laut Kuning melalui wilayah selatan Teluk Korea. Referensi Tom McKnight...

America's first practical gasoline automobile Motor vehicle The 1891 Buckeye Gasoline BuggyOverviewProduction1890Model years1891DesignerJohn William Lambert, inventor The Buckeye gasoline buggy, also known as the Lambert gasoline buggy, was an 1891 gasoline automobile, the first made in the United States. It was also the first automobile made available for sale in the United States. It was initially a three-wheel horseless carriage, propelled by an internal combustion gasoline engine; it...

Australian author (1870–1946) Henry Handel RichardsonHenry Handel/Ethel Florence Lindesay Richardson in 1945, a year before her deathBornEthel Florence Lindesay Richardson(1870-01-03)3 January 1870East Melbourne, Victoria, AustraliaDied20 March 1946(1946-03-20) (aged 76)Hastings, East Sussex, EnglandLanguageEnglishNationalityAustralianYears active1895-1940Notable worksThe Fortunes of Richard Mahony Ethel Florence Lindesay Richardson (3 January 1870 – 20 March 1946),...

Subgroup of Slavic peoples who speak the South Slavic languages This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: South Slavs – news · newspapers · books · scholar · JSTOR (June 2022) (Learn how and when to remove this template message) South Slavs Countries where a South Slavic language is the nati...

2008 film by Gurinder Chadha Angus, Thongs and Perfect SnoggingTheatrical release posterDirected byGurinder ChadhaScreenplay by Gurinder Chadha Paul Mayeda Berges Will McRobbChris Viscardi Based onAngus, Thongs and Full-Frontal Snogging and It's OK, I'm Wearing Really Big Knickersby Louise RennisonProduced by Gurinder Chadha Lynda Obst Starring Georgia Groome Alan Davies Karen Taylor Aaron Johnson Eleanor Tomlinson CinematographyRichard PopeEdited by Justin Krish Martin Walsh Music byJoby Tal...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2021) اضغط هنا للاطلاع على كيفية قراءة التصنيف سحلية الخشب بن زايد حالة الحفظ أنواع غير مهددة أو خطر انقراض ضعيف جدا[1] المرتبة التصنيفية نوع التصن�...

River in Sonora, MexicoRio SonoraSonora RiverPortion of the watercourse of the Sonora River, as it passes through La EstanciaLocation of mouthLocationCountryMexicoStateSonoraPhysical characteristicsMouth • locationGulf of California • coordinates28°51′12″N 111°59′27″W / 28.8532°N 111.9908°W / 28.8532; -111.9908Length402 km (250 mi)Basin size10,040 km2 (3,880 sq mi) Río Sonora (Sonora River...

Home video game console N64 redirects here. For other uses, see N64 (disambiguation). Nintendo 64A black Nintendo 64 (right) and light gray Nintendo 64 controllerAlso known as Project Reality (code name) Ultra 64 (planned product name) Hyundai Comboy 64 (South Korea) DeveloperNintendo IRDManufacturerNintendoTypeHome video game consoleGenerationFifthRelease dateJP: June 23, 1996[3]NA: September 29, 1996[1][2]EU/AU: March 1, 1997[4][5]Lifespan1996 (1...

Chinese-American financial services businessman For the Chinese football player, see Zhao Peng. Peng Zhao赵鹏Peng Zhao, May 2013Born1982 or 1983 (age 40–41)[1]Beijing, China[2]Alma materUniversity of California, Berkeley (PhD)[2]Peking UniversityOccupationBusinessmanYears active2006-presentEmployerCitadel SecuritiesTitleCEO (2017-present)Board member ofThe Asian American Foundation[3]SpouseCherry Chen Peng Zhao (Chinese: ...

Parque Anchieta Bairro do Brasil Localização Distrito Zona Norte História Criado em 15 de novembro de 1999 Características geográficas Área total 390,58 ha (em 2003) População total 26 212 (em 2 010)[1] hab. • IDH 0,833[2](em 2000) Outras informações Domicílios 9 307 (em 2010) Limites Anchieta, Ricardo de Albuquerque, Vila Militar, Realengo e Nilópolis[3] Subprefeitura Zona Norte Parque Anchieta é um pequeno bairro da Zona Norte do município ...

S02 Boulevard UtaraStasiun LRT JakartaTampak dari Mall Kelapa Gading 1Nama lainSummarecon Kelapa Gading, Mall Kelapa GadingLokasiJalan Boulevard Raya, Kelapa Gading Timur, Kelapa Gading, Jakarta UtaraJakartaIndonesiaKoordinat6°09′34″S 106°54′22″E / 6.1594°S 106.906°E / -6.1594; 106.906Koordinat: 6°09′34″S 106°54′22″E / 6.1594°S 106.906°E / -6.1594; 106.906PemilikPemprov DKI JakartaPengelolaJakarta PropertindoJalurS Lin 1J...

2006 filmAmerican HardcoreMovie posterDirected byPaul RachmanWritten bySteven BlushProduced by Steven Blush Paul Rachman StarringVarious musicians, entertainment executives, etc.Distributed bySony PicturesRelease date September 22, 2006 (2006-09-22) LanguageEnglish American Hardcore: The History of American Punk Rock 1980–1986 is a documentary directed and produced by Paul Rachman and written by Steven Blush.[1][2] It is based on the 2001 book American Hardcor...

2001 studio album by Neil DiamondThree Chord OperaStudio album by Neil DiamondReleasedJuly 24, 2001Recorded2000-01GenrePopLength47:17LabelColumbiaProducerPeter Asher, Alan LindgrenNeil Diamond chronology The Neil Diamond Collection(1999) Three Chord Opera(2001) The Essential Neil Diamond(2001) Professional ratingsReview scoresSourceRatingAllMusic[1] Three Chord Opera is the twenty-fifth studio album by Neil Diamond, released in 2001. It marked the first album since 1974's Sere...

Das Comitetul Olimpic și Sportiv Român (kurz: COSR) ist das nationale Olympische Komitee in Rumänien. Inhaltsverzeichnis 1 Geschichte 2 Vorsitzende 3 Weblinks 4 Einzelnachweise Geschichte Es wurde 1914 unter dem Namen „Comitetul Olimpic Român“ gegründet. 1924 nahm Rumänien in Paris zum ersten Mal an den Olympischen Spielen teil. Seitdem hat Rumänien an allen Spielen teilgenommen, mit Ausnahme der Sommerspiele von 1932 und 1948 und der Winterspiele von 1960. Auch an den Sommerspiele...

Traditional mother of MaryFor the figure of Luke 2, see Anna the Prophetess. For other uses, see Saint Anne (disambiguation). SaintAnneGreek icon of Saint Anne with the Virgin, by Angelos AkotantosMother of the Virgin, Maternal Heroine, Woman of AmramBornbefore c. 49 BCBethlehem, Hasmonean JudeaDiedafter c. 4 ADVenerated inOrthodox ChurchEastern Catholic ChurchesRoman Catholic ChurchOriental Orthodox ChurchAnglican CommunionLutheranismIslamAfro-American religionCanonizedPre-C...