Loi log-logistique
| |||||||||||||||||||||||||||||
Read other articles:

Canadian film score composer (born 1946) This article is about the composer. For the entrepreneur, see Howard Shore (entrepreneur). For the judge, see Howard H. Shore. Howard Shore OCShore in 2013Background informationBirth nameHoward Leslie ShoreBorn (1946-10-18) October 18, 1946 (age 77)Toronto, Ontario, CanadaGenresFilm score, classicalOccupation(s)Composer, orchestrator, conductor, music producerInstrument(s)Piano, organ, clarinet, saxophone, fluteYears active1969–presentSpouse(s) ...

Diskografi ColdplayAlbum studio9Album rekaman langsung6Album kompilasi6Video musik63Extended play11Singel38 Diskografi Coldplay, sebuah band rock alternatif Britania Raya yang dibentuk pada tahun 1997, terdiri dari 9 album studio, 17 album mini, 37 singel, 6 album langsung, dan album kompilasi. Rilis pertama Coldplay, demo terbatas Safety, dirilis tahun 1998, dan album studio pertamanya, Parachutes, dirilis 2 tahun setelahnya, pada Juli 2000. Coldplay telah menjual lebih dari 50 juta album da...

Міхал ЛаскоМіхал Ерик Ласко Загальна інформаціяНаціональність полякГромадянство Республіка ПольщаНародження 11 березня 1981(1981-03-11) (42 роки)Вроцлав, ПольщаЗріст 202 смВага 104 кгСпортКраїна ІталіяВид спорту волейболКлуб «Ястшембський Венґель»[1]Команда Verona Volleyd Участ

Останнє запитанняThe Last Question Жанр науково-фантастичне оповіданняdФорма оповіданняАвтор Айзек АзімовМова американська англійська і англійськаОпубліковано 1956Країна СШАПереклад А. Я. Минко, 1990Цикл Мультивак «Оста́ннє запита́ння» (англ. The Last Question) — науково-фанта

In 2006 werd het 92ste Campeonato Paranaense gespeeld voor voetbalclubs uit de Braziliaanse staat Paraná. De competitie werd gespeeld van 11 januari tot 9 april en werd georganiseerd door de Federação Paranaense de Futebol. Paraná werd kampioen. Eerste fase Groep A Plaats Club Wed. W G V Saldo Ptn. 1. Atlético Paranaense 14 8 4 2 38:20 28 2. Rio Branco 14 7 4 3 31:24 25 3. J. Malucelli 14 6 7 1 21:14 25 4. Iraty 14 6 3 5 32:25 21 5. Cianorte 14 5 4 5 26:29 19 6. Galo Maringá 14 4 2 8 17...

Ini adalah nama Tionghoa; marganya adalah Deng. Deng HuaLahir(1910-04-28)28 April 1910Hunan, TiongkokMeninggal3 Juli 1980(1980-07-03) (umur 70)PekerjaanJenderal Tentara Pembebasan Rakyat Deng Hua (Hanzi: 鄧華; Pinyin: Dèng Huá; 28 April 1910 – 3 Juli 1980) adalah seorang jenderal dalam Tentara Pembebasan Rakyat. Ia merupakan Wakil Komandan Tentara Sukarelawan Rakyat. Usai Marsekal Peng Dehuai pulang ke Tiongkok untuk berobat, Deng Hua menjadi Pelaksana Tugas K...

Lambang Søgne Søgne ialah sebuah kotamadya di provinsi Vest-Agder, Norwegia, yang merupakan kotamadya pesisir, dengan garis pantai yang panjang di selatan. Di timur berbatasan dengan kotamadya Kristiansand, di utara dan timur laut dengan Marnardal dan Songdalen, dan di barat dengan Mandal. Tak seperti kotamadya lain di Vest-Agder, Søgne tak mengalami penggabungan pada tahun-tahun terkini. Sebaliknya, Greipstad dipisahkan dari Søgne pada 1913 (dan pada 1964 bergabunglah Finsland ke Songdal...

Gen FM Surabaya (PM6FKC)PT Radio CamarKotaSurabayaWilayah siarGerbangkertosusila dan sekitarnyaSloganSuara Musik Terkini (1 Maret 2010-31 Juli 2017)Generasi Suara Musik Indonesia (1 Agustus 2017-sekarang)Hits Abis! (tagline, 1 Januari 2017-31 Desember 2017)Pol! (tagline, 1 Januari 2018-31 Desember 2018)Wani Pol! (tagline, 1 Januari 2019-sekarang)Frekuensi103.1 FMMulai mengudara1 Maret 2010; 13 tahun lalu (2010-03-01)FormatChr (Top40)Otoritas perizinanKementerian Komunikasi dan Informatik...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Ethiopia–Greece relations – news · newspapers · books · scholar · JSTOR (April 2012) Bilateral relationsEthiopian-Greek relations Ethiopia Greece Ethiopian-Greek relations are the international relations between Ethiopia and Greece. In general, bila...

Armee-Abteilung GaedeArmee-Abteilung BArmy Detachment BFlag of the Staff of an Armee Oberkommando (1871–1918)Active19 September 1914 – post 11 November 1918Country German EmpireTypeArmyEngagementsWorld War IMilitary unit Armee-Abteilung Gaede / Armee-Abteilung B (Army Detachment B) was an army level command of the German Army in World War I. It served on the Western Front throughout its existence and formed the extreme left wing (up against the Swiss Border). History After the 7th Ar...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Simca Rush engine – news · newspapers · books · scholar · JSTOR (October 2022) Reciprocating internal combustion engine Simca Rush engineOverviewProduction1960-1964LayoutConfigurationStraight-fourDisplacement79 cubic inches (1,290 cc)Cylinder bor...

Nota: Para outros significados, veja A (desambiguação). Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Dezembro de 2015) A a Àà AA letra nas versões de fôrma e cursiva, maiúsculas e minúsculas. Sistema de escrita alfabeto latino Representações alternativas Alfabeto...

Asian Film ArchiveFounder(s)Tan Bee ThiamEstablished2005MissionSave, explore and share the art of Asian CinemaChairGlen GoeiStaff11-15Key peopleKaren ChanAddress100 Victoria St.#04-01 National Library Building, Singapore 188064LocationSingapore, SingaporeCoordinates1°17'51.7N 103°51'16.4EWebsitehttp://www.asianfilmarchive.orgThe Asian Film Archive (AFA) is a non-governmental organisation in Singapore that preserves the film heritage of Asian Cinema. The archive is located at the National Li...

Rapid transit station in San Francisco Bay Area For the film, see Fruitvale Station. FruitvaleFruitvale station in March 2018General informationLocation3401 East 12th StreetOakland, CaliforniaCoordinates37°46′29″N 122°13′27″W / 37.7748°N 122.2241°W / 37.7748; -122.2241Owned bySan Francisco Bay Area Rapid Transit DistrictLine(s)BART A-LinePlatforms2 side platformsTracks2Connections AC Transit: O, 1T, 14, 19, 20, 21, 39, 47, 51A, 54, 62, 706, 801, 851Construc...

Dieser Artikel behandelt das Sechskaiserjahr 238 n. Chr. Für das manchmal irrtümlich als Sechskaiserjahr bezeichnete Zweite Vierkaiserjahr 193 n. Chr. siehe ebenda. Als Sechskaiserjahr wird das Jahr 238 n. Chr. bezeichnet. Die chaotischen, teils bürgerkriegsartigen Ereignisse dieser Monate gelten als eine der schwersten Regierungskrisen der römischen Geschichte und offenbarten strukturelle Probleme des Kaisertums am Ende der Epoche des Prinzipats, die erst in der Spätantike vorläufig ü...

Submarine of the Royal Navy For other ships with the same name, see HMS Undaunted. History United Kingdom NameHMS Undaunted BuilderVickers Armstrong, Barrow-in-Furness Laid down2 December 1939 Launched20 August 1940 Commissioned30 December 1940 FateSunk 11 May 1941 Badge General characteristics Displacement Surfaced - 540 tons standard, 630 tons full load Submerged - 730 tons Length58.22 m (191 feet) Beam4.90 m (16 ft 1 in) Draught4.62 m (15 ft 2 in) Propulsion 2 shaft diesel-electric 2 Paxma...

Divinyl ether Names Preferred IUPAC name (Ethenyloxy)ethene Other names divinyl ether, divinyl oxide, ethenoxyethene Identifiers CAS Number 109-93-3 3D model (JSmol) Interactive image ChEBI CHEBI:81293 ChEMBL ChEMBL2105883 ChemSpider 7733 ECHA InfoCard 100.003.383 EC Number 203-720-5 KEGG C17721 PubChem CID 8024 UNII 2H2T044E11 UN number 1167 CompTox Dashboard (EPA) DTXSID5074555 InChI InChI=1S/C4H6O/c1-3-5-4-2/h3-4H,1-2H2Key: QYKIQEUNHZKYBP-UHFFFAOYSA-N SMILES O(\C=C)\C=C Properties Che...

2013 Indian filmGundello GodariPromotional posterDirected byKumar NagendraProduced byLakshmi ManchuStarring Aadhi Pinisetty Taapsee Pannu Lakshmi Manchu Sundeep Kishan CinematographyM. R. Palani KumarMusic byIlaiyaraajaProductioncompanyManchu EntertainmentDistributed byBlueSky (overseas)[1]Release date 8 March 2013 (2013-03-08) Running time131 minutesCountryIndiaLanguageTeluguBudget₹5 Crore[2] Gundello Godari is a 2013 Indian Telugu-language adventure drama fi...

Airport in New South Wales, AustraliaCoolah AirportIATA: CLHICAO: YCAHSummaryAirport typePublicOperatorWarrumbungle Shire CouncilLocationCoolah, New South Wales, AustraliaElevation AMSL1,074 ft / 327 mCoordinates31°46′24″S 149°36′36″E / 31.77333°S 149.61000°E / -31.77333; 149.61000MapYCAHLocation in New South WalesRunways Direction Length Surface m ft 08/26 1,074 3,524 Gravel Sources: Australian AIP[1] Coolah Airport (IATA: CLH, ICAO:...

1943 British filmDear OctopusDirected byHarold FrenchWritten byPatrick KirwanR. J. Minney Esther McCracken (adaptation)Based onthe play by Dodie SmithProduced byEdward BlackStarringMargaret LockwoodMichael WildingCelia JohnsonCinematographyArthur CrabtreeEdited byMichael C. ChorltonMusic byHubert BathProductioncompanyGainsborough PicturesDistributed byGeneral Film Distributors (UK)Release date 20 September 1943 (1943-09-20) (UK) Running time86 minutesCountryUnited KingdomLa...

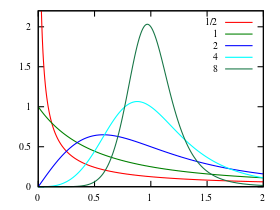

![{\displaystyle {\frac {(\beta /\alpha )(x/\alpha )^{\beta -1}}{\left[1+(x/\alpha )^{\beta }\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/994256a885337671244a0e4ebd6e0a34dd279339)





![{\displaystyle f(x;\alpha ,\beta )={\frac {(\beta /\alpha )(x/\alpha )^{\beta -1}}{\left[1+(x/\alpha )^{\beta }\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd0260903331849f03331dbb227d754cdeab3492)











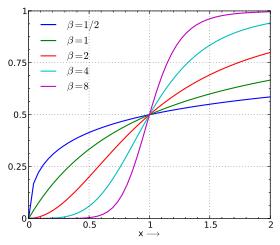
![{\displaystyle S(t)=1-F(t)=\left[1+\left({\frac {t}{\alpha }}\right)^{\beta }\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd572e48bb4240ae7b60577af67734dcfd38c13b)

![{\displaystyle H(t)=-\log(S(t))=\log \left[1+\left({\frac {t}{\alpha }}\right)^{\beta }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76189493fbce64e01672f3c7f0b74c1d7bd3ccb8)






