Anneau cohérent
|
Read other articles:

I patrimoni dell'umanità dell'Algeria sono i siti dichiarati dall'UNESCO come patrimonio dell'umanità in Algeria, che è divenuta parte contraente della Convenzione sul patrimonio dell'umanità il 24 giugno 1974[1]. Al 2022 i siti iscritti nella Lista dei patrimoni dell'umanità sono sette, mentre sei sono le candidature per nuove iscrizioni[1]. Il primo sito iscritto nella lista è stata nel 1980 la Qal'a dei Banu Hammad, durante la quarta sessione del comitato del patrimon...

British-American actress (1903-1990) Dorothy MackaillPublicity photo of Mackaill from Stars of the Photoplay, 1924Born(1903-03-04)March 4, 1903Sculcoates, Hull, East Riding of Yorkshire, EnglandDiedAugust 12, 1990(1990-08-12) (aged 87)Honolulu, Hawaii, U.S.CitizenshipBritishAmericanOccupationActressYears active1920–1937; 1976–1980Spouse(s) Lothar Mendes (m. 1926; div. 1928) Neil Miller (m. 19...

Jalan Tol Ulujami–SerpongInformasi ruteDikelola oleh PT. Nusantara Infrastructure (Pondok Aren-Serpong)PT Jasa Marga (Persero) Tbk (Ulujami-Pondok Aren)Panjang:12.5 km (7,8 mi)Berdiri:1999; 24 tahun lalu (1999) – sekarangSejarah:Dibangun tahun 1999-20051999 (Serpong-Pondok Aren)2002 (Pondok Aren-Bintaro Viaduct)2005 (Bintaro Viaduct-Ulujami) 2022 (Serpong-Cisauk September 2023 (Cisauk-Legok) Januari 2024 (Tahap pembangunan balaraja, sebagai perencanaan Tol Jakarta Merak)Persimpan...

Європейські легкоатлетичні ігри в приміщенні 1968 Європейські легкоатлетичні ігри в приміщенні 1968Загальна інформаціяМісто МадридКраїни-учасниці 20Кількість атлетів 205Розігрується медалей 23 комплектиВідкриття 9 березняЗакриття 10 березняАрена Палац спорту[es]← 1967 Праг...

Part of a series onBritish law Acts of Parliament of the United Kingdom Year 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820–1824 1825–1829 1830–1834 1835–1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850–1854 1855–1859 1860–1864 1865–1869 1870–1875 1876 1877 1878 1879 1880–1883 1884 1885–1889 1890–1894 1895–1899 1900 1901 1902 1903 1904 1905 1906 1907 1908 1909 1910 1911 1912 1913 1914 1915 1916 1917 1918...

American politician Jim DabakisDabakis in 2013Member of the Utah State Senatefrom the 2nd districtIn officeDecember 2012 – January 2019Preceded byBen McAdamsSucceeded byDerek KitchenChair of the Utah Democratic PartyIn officeJuly 2011 – March 2014Preceded byWayne HollandSucceeded byPeter Corroon Personal detailsBorn1953 or 1954 (age 69–70)[1]Political partyDemocratic (until 2020)Republican (2020-present)[a]SpouseStephen Justesen Jim Dab...

This is a list of open-wheel single seater formula racing motorsport champions in the Formula Regional class. This list contains only those championships that operate using the vehicle regulations launched by the FIA Single Seater Commission in December 2017.[1] Series Formula Regional Americas Championship 2019 Formula Regional Americas champion Dakota Dickerson at Road America. Season Driver Team Car 2018 Kyle Kirkwood Abel Motorsports Ligier–Honda JS F3 [2] 2019 Dakota Di...

Public school in Pembroke Pines, Florida West Broward High SchoolAddress500 NW 209th AvePembroke Pines, Florida 33029United StatesCoordinates26°00′42″N 80°25′47″W / 26.011539°N 80.429645°W / 26.011539; -80.429645InformationTypePublicEstablishedAugust 20, 2008 (2008-08-20)School districtBroward County Public SchoolsNCES District ID1200180[1]SuperintendentRobert RuncieCEEB code102181NCES School ID120018007555[2]PrincipalBrad Fat...

У Вікіпедії є статті про інших людей із прізвищем Кривоносов. Сергій Сергійович Кривоносов Підполковник Загальна інформаціяНародження 26 червня 1978(1978-06-26)м. МиколаївСмерть 4 серпня 2014(2014-08-04) (36 років)Луганська областьПоховання МиколаївПсевдо ГранітВійськова службаПр...

此條目需要更新。 (2010年2月17日)請更新本文以反映近況和新增内容。完成修改後請移除本模板。 战争列表:公元1000年以前—1000年-1499年—1500年-1799年—1800年-1899年—1900年-1944年—1945年-1989年—1990年-2002年—2003年至今 本表收录了2003年以后新近爆发的世界各地武装冲突和战争。 开始年份 结束年份 冲突名称 交战方 胜利方 战败方 2003 2010 达尔富尔冲突 苏丹政府�...

Fereydoon HoveydaPermanent Representative of Iran to the United NationsIn office1971–1979Prime MinisterAmir-Abbas HoveydaJamshid AmouzegarJafar Sharif-EmamiGholam Reza AzhariShapour BakhtiarPreceded byMehdi VakilSucceeded byMansour Farhang Personal detailsBorn21 September 1924Damascus, State of SyriaDied3 November 2006(2006-11-03) (aged 82)Clifton, Virginia, United StatesNationalityIranianPolitical partyRastakhiz PartyOccupationDiplomat, writer, film criticWebsiteOfficial website Ferey...

Kandi FödelsenamnKandi BurrussFödd17 maj 1976 (47 år)Bakgrund Atlanta, Georgia, USAGenrerR&B, soul, hiphopRollSångerska, låtskrivare, musikproducent, skådespelareÅr som aktiv1992 –SkivbolagCapitol Records (2000) Kandi Koated Records / Asylum Records (2010– )ArtistsamarbetenTLC, Mariah Carey, Alicia Keys, Destinys ChildWebbplatsOfficiell webbplats Kandi Burruss-Tucker, född den 17 maj 1976 i Atlanta, Georgia, är en amerikansk Grammy Award-vinnande R&B-sångerska, musi...
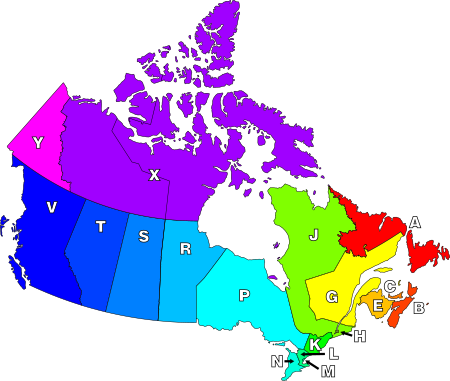
Kodepos Kanada NL NS PE NB QC ON MB SK AB BC NU/NT YT A B C E G H J K L M N P R S T V X Y Yukon - 3 FSA Y0AYukon Tenggara(Watson Lake) Y1AWhitehorse Y0BYukon Tengah(Dawson City) Y1BBelum disetujui Y0CBelum disetujui Y1CBelum disetujui Y0EBelum disetujui Y1EBelum disetujui Y0GBelum disetujui Y1GBelum disetujui Y0HBelum disetujui Y1HBelum disetujui Y0JBelum disetujui Y1JBelum disetujui Y0KBelum disetujui Y1KBelum disetujui Y0LBelum disetujui Y1LBelum disetujui Y0MBelum disetujui Y1MBelum diset...

El Francocomune El Franco – Veduta LocalizzazioneStato Spagna Comunità autonoma Asturie Provincia Asturie TerritorioCoordinate43°33′00″N 6°52′00.12″W43°33′00″N, 6°52′00.12″W (El Franco) Altitudine62 m s.l.m. Superficie78 km² Abitanti4 123 (2001) Densità52,86 ab./km² Altre informazioniCod. postale33... Prefisso(+34)... Fuso orarioUTC+1 Codice INE33023 TargaO CartografiaEl Franco El Franco – Mappa Sito istituzionaleModifica dati su ...

Street in East Sussex, England Dumb Woman's LaneStreet sign of Dumb Woman's LaneLocationUdimorePostal codeTN31Coordinates50°56′26″N 0°41′58″E / 50.9406°N 0.6995°E / 50.9406; 0.6995 Dumb Woman's Lane is a street located in the civil parish of Udimore, near Winchelsea in East Sussex, England. The street has achieved a level of notoriety because of its unusual name. While the etymology remains unconfirmed, sources attribute it to a mute woman (the word dumb on...

1994 studio album by The RippingtonsSaharaStudio album by The RippingtonsReleasedAugust 30, 1994Recorded1994GenreSmooth jazz, jazz fusionLength46:06LabelGRPProducerRuss FreemanThe Rippingtons chronology Live in L.A.(1992) Sahara(1994) Brave New World(1996) Sahara is the eighth album by American Jazz group The Rippingtons, released in 1994 on the GRP label. The album reached number two on Billboard's contemporary Jazz chart. It is also the first of two studio albums to be released unde...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (September 2016) Straight Branch is a tributary of South Deepwater Creek in Bates County, in the U.S. state of Missouri.[1] Straight Branch was so named because of its relatively straight watercourse.[2] See also List of rivers of Missouri References ^ U.S. Geological Survey Geographic Names Information System: Straight ...

Hippocrepis comosa Estáu de caltenimientuEsmolición menor (IUCN)Clasificación científicaReinu: PlantaeDivisión: MagnoliophytaClas: MagnoliopsidaSubclas: RosidaeOrde: FabalesFamilia: FabaceaeSubfamilia: FaboideaeTribu: LoteaeXéneru: HippocrepisEspecie: Hippocrepis comosaL.ConsultesRoyal Botanic Gardens, Kew Royal Botanic Gardens, KewWorld Flora Online World Flora online[editar datos en Wikidata] Hippocrepis comosa ye un arbustu de la familia de les fabacees. Ye orixinaria de la rexón d...

Cet article est une ébauche concernant un homme politique américain. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir Fulton. William S. Fulton Fonctions Sénateur des États-Unisreprésentant l'Arkansas 18 septembre 1836 – 15 août 1844(7 ans, 10 mois et 28 jours) Prédécesseur Poste créé Successeur Chester Ashley 5e gouverneur du territoire de l'Arkansas 9...

В Википедии есть статьи о других людях с такой фамилией, см. Ямщиков. Ямщиков, Валерий Сергеевич Дата рождения 15 августа 1937(1937-08-15) Дата смерти 11 июля 1996(1996-07-11) (58 лет) Место смерти Москва Страна СССР → Россия Род деятельности учёный Научная сфера Горное дело М...














































