PROFILBARU.COM

正四角錐
類別	Johnson多面體 ; J92 – J1 – J2
對偶多面體	正四角錐（自身對偶）
識別
鮑爾斯縮寫; （verse-and-dimensions的wikia：Bowers acronym）	squippy
數學表示法
施萊夫利符號	()∨{4}
性質
面	5
邊	8
頂點	5
歐拉特徵數	F=5, E=8, V=5 （χ=2）
組成與佈局
面的種類	正三角形×4 ; 正方形×1
頂點佈局; （英语：Vertex_configuration）	4(32.4); (34)
對稱性
對稱群	C4v, [4], (*44)
旋轉對稱群; （英語：Rotation_groups）	C4, [4]+, (44)
特性
	凸
圖像
	; （展開圖）
	; （展開圖）
	查; 论; 编;

四角錐是底面為四邊形的錐體。

種類

底面為長方形的四角錐。

底面為正方形的四角錐。通常是指側邊同時還是等腰三角形的四角錐。

特別地，側面也為正三角形的正四角錐是一種詹森多面體。

底面凹四邊形的四角錐。底面邊有交叉的也屬於凹四角錐（嚴格來說，應成為非凸四角錐）稱為交叉四角錐，其中星形帳塔可以分割成數個交叉四角錐。

在Johnson多面體當中J₁是一個以正方形為底並和其它四個正三角形所構成的四角錐，是Johnson多面體中構造最簡單的一個，形似金字塔。同時它也是柏拉圖立體中正八面體的一半。最早在1966年首先被諾曼·詹森（英语：Norman Johnson (mathematician)）命名和描述。

J₁共有8個邊、5個面、5個頂點。若設其一邊為 $a$ ，體積為 $V$ ，高為 $H$ ，則：

H={\frac {1}{\sqrt {2}}}a

A=(1+{\sqrt {3}})a^{2}

V={\frac {\sqrt {2}}{6}}a^{3}


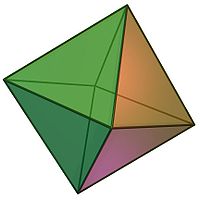
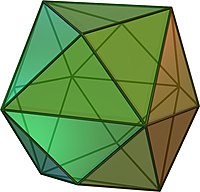
正八面體可由兩個Johnson多面體中的J₁底面對底面疊在一起組成。	四角化六面體(Tetrakis Hexahedron)為卡塔蘭立體的其中一個，可由一個正方體的每一面疊一個正四角錐組成。

棱锥体
正二棱錐	正三棱錐	正四棱錐	正五棱錐	正六棱錐	正七棱錐	正八棱錐	正九棱錐	正十棱錐	...	圆锥

錐體形式鑲嵌系列：
球面鑲嵌		錐體									歐式鑲嵌仿緊空間	雙曲鑲嵌非緊空間
一角錐 C_1v, [1]	二角錐 C_2v, [2]	三角錐 C_3v, [3]	四角錐 C_4v, [4]	五角錐 C_5v, [5]	六角錐 C_6v, [6]	七角錐 C_7v, [7]	八角錐 C_8v, [8]	九角錐 C_9v, [9]	十角錐 C_10v, [10]	...	無限角錐 C_∞v, [∞]	超無限角錐 C_iπ/λv, [iπ/λ]