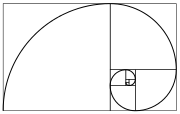
Послідовність Фібоначчі
|
Read other articles:

В Википедии есть статьи о других людях с такой фамилией, см. Дерюгин. Борис Иванович Дерюгин 8-й председатель Хабаровского крайисполкома 18 декабря 1960 года — 4 мая 1962 года Предшественник Котов, Федор Прокофьевич Преемник Чёрный, Алексей Клементьевич 9-й второй секретарь О

Чемпионат Дагестана по футболу Основан 1936 Регион Дагестан Число участников 11 Действующий победитель Леки (Магарамкент) Наиболее титулован Труд (Каспийск) — 13 раз 2022 Чемпионат Республики Дагестан по футболу — соревнование среди любительских команд в Дагестане. Футбол

Falkenhagener Feld Ortsteil von Berlin Falkenhagener Feld auf der Karte von Spandau. Koordinaten 52° 32′ 49″ N, 13° 10′ 40″ O52.54694444444413.177777777778Koordinaten: 52° 32′ 49″ N, 13° 10′ 40″ O Fläche 6,879 km² Einwohner 39.477 (31. Dez. 2022) Bevölkerungsdichte 5739 Einwohner/km² Postleitzahlen 13583, 13589 Ortsteilnummer 0508 Bezirk Spandau Falkenhagener Feld Kreuzung Falkenseer Chaussee / ...

Pembagian negara merupakan pembagian wilayah suatu negara berdasarkan sistem tertentu dengan maksud untuk mempermudah administrasi, pemerintahan, dan hal-hal yang sehubungan dengan itu. Hasil dari pembagian tersebut dikenal dengan sebutan umum subdivisi negara atau pembagian negara. Berbeda dengan batas-batas geografi yang kasatmata seperti sungai, gunung, gurun, dan semacamnya, pembagian negara merupakan suatu hal yang abstrak (tak kasatmata). Pembagian negara yang paling umum adalah pembagi...

Impatiens textorii Klasifikasi ilmiah Kerajaan: Plantae Divisi: Tracheophyta Kelas: Magnoliopsida Ordo: Ericales Famili: Balsaminaceae Genus: Impatiens Spesies: Impatiens textorii Nama binomial Impatiens textoriiMiq. Impatiens textorii adalah spesies tumbuhan yang tergolong ke dalam famili Balsaminaceae. Spesies ini juga merupakan bagian dari ordo Ericales. Spesies Impatiens textorii sendiri merupakan bagian dari genus Impatiens.[1] Nama ilmiah dari spesies ini pertama kali diterbitka...

Aeropuerto Internacional Lal Bahadur Shastri लाल बहादुर शास्त्री हवाई अड्डे IATA: VNS OACI: VIBN FAA: LocalizaciónUbicación Benarés, Uttar Pradesh, India, IndiaElevación 81Sirve a BenarésDetalles del aeropuertoTipo CivilOperador Dirección de Aeropuertos de IndiaPistas DirecciónLargoSuperficie09/272.206AsfaltoSitio web https://www.aai.aero/en/airports/varanasi[editar datos en Wikidata] El Aeropuerto Internacional Lal Bahadur ...

Halaman ini berisi artikel tentang lagu The Cranberries. Untuk album dan lagu Fela Kuti, lihat Zombie (album). ZombieSampul standar (edisi CD/Vinyl)Lagu oleh The Cranberriesdari album No Need to ArgueDirilis19 September 1994Format CD single video single Direkam1994 di Windmill Lane StudiosGenreHard rockRock alternatifpost-grungeDurasi5:06 (album/video #1)4:11 (video #2/radio)LabelIslandPenciptaDolores O'RiordanProduserStephen StreetVideo musikZombie di YouTube Zombie adalah lagu protes band r...

Coppa del Mondo di rugby 20232023 Rugby World CupCoupe du Monde de rugby 2023 Competizione Coppa del Mondo di rugby Sport Rugby a 15 Edizione 10ª Organizzatore World Rugby e Fédération Française de Rugby Date dall'8 settembre 2023al 28 ottobre 2023 Luogo Francia Partecipanti 20 (33 alle qualificazioni) Formula fase a gironi + play-off Sede finale Stade de France (Saint-Denis) Direttore Julien Collette Risultati Vincitore Sudafrica(4º titolo) Finalista Nuova Zelanda Terzo In...

Logo des NHS National Health Service (NHS; deutsch Nationaler Gesundheitsdienst) bezeichnet das staatliche Gesundheitssystem im Vereinigten Königreich. Der NHS agiert in vier weitgehend eigenständigen Organisationen in England, Wales, Schottland und Nordirland und versorgt rund 65,5 Millionen Menschen medizinisch. 2015 hatte der NHS ein Finanzvolumen von umgerechnet 251,2 Milliarden Euro.[1] Insgesamt beschäftigten die vier regionalen Bereiche 2016 um die 1,7 Mio. Angestellte....

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر مغاير للذي أنشأها؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (ديسمبر 2018) الرضاعة الطبيعية الأماكن العامة هي ممارسة رضاعة الأطفا�...

Title page of Delitiae Musicae Joachim van den Hove (1567? – 1620) was a Flemish/Dutch composer and a lutenist. He composed works for lute solo and for lute and voice. Moreover, he wrote many arrangements for lute of Italian, French, and English vocal and instrumental music, and of Flemish/Dutch folk music. Van den Hove disputes with Adriaensen and Vallet the distinction of being the most important representative of 17th century Dutch lute music. Van den Hove was born in Antwerp, where ...

Not to be confused with Taqwacore (film). 2010 American filmThe TaqwacoresTheatrical release posterDirected byEyad ZahraScreenplay byEyad ZahraMichael Muhammad KnightStory byMichael Muhammad Knight (novel)Produced byDavid PerseAllison CarterNahal AmeriStarringDominic RainsBobby NaderiNoureen DeWulfCinematographyJP PerryEdited byJosh RosenfieldMusic byOmar FadelRelease date January 24, 2010 (2010-01-24) (Sundance) CountryUnited StatesLanguageEnglish The Taqwacores is a 2010 ...

Embalse de Vilar Ubicación geográficaCoordenadas 40°59′12″N 7°32′08″O / 40.98666667, -7.53555556Ubicación administrativaPaís PortugalDivisión Moimenta da Beira y SernancelheDatos generalesOperador Energías de PortugalCuerpo de aguaLongitud 240 metrosAltitud 552 metrosCentralPotencia instalada 64 megavatios[editar datos en Wikidata] El embalse de Vilar es una represa portuguesa erguida en el río Távora, cerca de la aldea de Vilar (Moimenta da Beira),...

American judge (born 1961) Xavier RodriguezRodriguez in 2019Judge of the United States District Court for the Western District of TexasIncumbentAssumed office August 1, 2003Appointed byGeorge W. BushPreceded byEdward C. PradoAssociate Justice of the Supreme Court of TexasIn officeSeptember 7, 2001 – November 6, 2002Appointed byRick PerryPreceded byGreg AbbottSucceeded bySteven Wayne Smith Personal detailsBornXavier Rodriguez (1961-09-20) September 20, 1961 (age 62)[1&#...

This article is about the neighborhood in Haifa. For the Jerusalem neighborhood, see Romema. Romema, Haifa Romema (Hebrew: רוממה) is a neighborhood in the city of Haifa, Israel. Also known as The Romemot and Ramat Ben-Gurion, it is located east of Ahuza, on the northern slope of Mount Carmel. Today the neighborhood has two sections - New Romema and Old Romema - with a joint population of 8,340.[1] Etymology Rushmiya comes from a personal name.[2] History Khirbet Rushmiya ...

American television series The ImpossiblesTitle cardDirected byWilliam HannaJoseph BarberaStarringPaul FreesDon MessickHal SmithCountry of originUnited StatesNo. of seasons1No. of episodes18ProductionProducersWilliam HannaJoseph BarberaRunning time6 minutesProduction companyHanna-Barbera ProductionsOriginal releaseNetworkCBSReleaseSeptember 10, 1966 (1966-09-10) –January 7, 1967 (1967-01-07) The Impossibles is a series of American animated cartoons produced by Hanna-Barbera i...

松田由太郎 1950年天皇賞(春)優勝時(41歳)基本情報国籍 日本出身地 京都府京都市下京区生年月日 1909年3月25日死没 2002年7月30日(満92歳没)騎手情報所属団体 阪神競馬倶楽部日本競馬会所属厩舎 伊藤勝吉・鳴尾(1923年-1937年)調騎兼業・鳴尾(1937年-1944年)初免許年 1926年免許区分 平地・障害騎手引退日 1944年調教師情報初免許年 1937年調教師引退日 1990年2月28日(定...

Spanish long jumper This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) In this Spanish name, the first or paternal surname is Lame...

Train station in Winchester, Massachusetts, US Winchester CenterAn outbound train at Winchester Center station in August 2015General informationLocation29 Waterfield RoadWinchester, MassachusettsCoordinates42°27′06″N 71°08′16″W / 42.4516°N 71.1378°W / 42.4516; -71.1378Line(s)New Hampshire Main LinePlatforms2 side platformsTracks2Connections MBTA bus: 134ConstructionParking237 spaces (town permit required)Bicycle facilities27 spacesOther informationFare zone...

Ministerio Noruego de Infancia y Familia Barne- og familiedepartementet LocalizaciónPaís NoruegaInformación generalSigla BFDJurisdicción Gobierno de NoruegaTipo Ministerio de NoruegaSede Akersgata 59 - OsloOrganizaciónMinistros Kjell Ingolf Ropstad (KrF)Dirección Harald Nybøen (Secretario General)Dependencias Ombudsman de los Niños, Secretariat to the Market Council and the Consumer Disputes Commission, Norwegian Consumer Authority, Equality and Anti-Discrimination Ombud, Norwegian Di...






















![{\displaystyle F_{n}=\left[{\frac {\phi ^{n}}{\sqrt {5}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46f74f43bc2ce11609992c811979bc8e433839f0)


















































