–®–≤–ł–ī–ļ—Ė—Ā—ā—Ć
–ě—Ā–ļ—Ė–Ľ—Ć–ļ–ł –≤—Ė–ī–Ī—É–≤–į—Ē—ā—Ć—Ā—Ź –Ĺ–Ķ–Ņ–Ķ—Ä–Ķ—Ä–≤–Ĺ–į –∑–ľ—Ė–Ĺ–į –Ĺ–į–Ņ—Ä—Ź–ľ–ļ—É —Ä—É—Ö—É, –ļ–ĺ–Ľ–ł –≥–ĺ–Ĺ–ĺ—á–Ĺ—Ė –ľ–į—ą–ł–Ĺ–ł —Ä—É—Ö–į—é—ā—Ć—Ā—Ź –Ņ–ĺ –ļ—Ä–ł–≤–ĺ–Ľ—Ė–Ĺ—Ė–Ļ–Ĺ—Ė–Ļ –ī–ĺ—Ä—Ė–∂—Ü—Ė, —ó—Ö–Ĺ—Ź —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ĺ–Ķ —Ē —Ā—ā–į–Ľ–ĺ—é –°–ł–ľ–≤–ĺ–Ľ–ł:
v
{\displaystyle \mathbf {v} }
–ě–ī–ł–Ĺ–ł—Ü—Ė –≤–ł–ľ—Ė—Ä—é–≤–į–Ĺ–Ĺ—Ź –†–ĺ–∑–ľ—Ė—Ä–Ĺ—Ė—Ā—ā—Ć:
L T ‚ąí1 –ě–ī–ł–Ĺ–ł—Ü—Ė –≤–ł–ľ—Ė—Ä—é–≤–į–Ĺ–Ĺ—Ź:
–ľ/—Ā; m/s
–®–≤–ł–ī–ļ—Ė—Ā—ā—Ć —É –í—Ė–ļ—Ė—Ā—Ö–ĺ–≤–ł—Č—Ė
–ó–ľ–į–≥–į–Ĺ–Ĺ—Ź –Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –ī–≤–ĺ—Ö —Ą—É—ā–Ī–ĺ–Ľ—Ė—Ā—ā—Ė–≤ –®–≤–łŐĀ–ī–ļ—Ė—Ā—ā—Ć , –į–Ī–ĺ –Ņ–ĺ–≥—ĖŐĀ–Ĺ [ 1] —Ā–ļ–ĺŐĀ—Ä—Ė—Ā—ā—Ć [ 2] —Ö—ÉŐĀ—ā–ļ—Ė—Ā—ā—Ć [ 3] –Ņ—Ä—ÉŐĀ–ī–ļ—Ė—Ā—ā—Ć [ 4] –Ī–ł—Ā—ā—Ä–ĺ—ā–įŐĀ [ 5] —Ą—Ė–∑–ł—á–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į , —Č–ĺ –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–į—Ē –≤—Ė–ī–Ĺ–ĺ—ą–Ķ–Ĺ–Ĺ—é –Ņ–Ķ—Ä–Ķ–ľ—Ė—Č–Ķ–Ĺ–Ĺ—Ź —ā—Ė–Ľ–į –ī–ĺ –Ņ—Ä–ĺ–ľ—Ė–∂–ļ—É —á–į—Ā—É , –∑–į —Ź–ļ–ł–Ļ –≤—Ė–ī–Ī—É–≤–į–Ľ–ĺ—Ā—Ź –Ņ–Ķ—Ä–Ķ–ľ—Ė—Č–Ķ–Ĺ–Ĺ—Ź. –®–≤–ł–ī–ļ—Ė—Ā—ā—Ć ‚ÄĒ –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–į , —ā–ĺ–Ī—ā–ĺ –≤–ĺ–Ĺ–į –ľ–į—Ē –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź (–ľ–ĺ–ī—É–Ľ—Ć) —Ė –Ĺ–į–Ņ—Ä—Ź–ľ–ĺ–ļ.
–®–≤–ł–ī–ļ—Ė—Ā—ā—Ć, —Ź–ļ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –∑–ī–Ķ–Ī—Ė–Ľ—Ć—ą–ĺ–≥–ĺ –Ņ–ĺ–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź –Ľ—Ė—ā–Ķ—Ä–ĺ—é
v
{\displaystyle \mathbf {v} }
v
→ ‚Üí -->
{\displaystyle {\vec {v}}}
v
{\displaystyle v}
–Ľ–į—ā. Velocitas ‚ÄĒ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć).
–£ —Ā–ł—Ā—ā–Ķ–ľ—Ė SI —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć (—ā–ĺ—á–Ĺ—Ė—ą–Ķ —ó—ó –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į ) –≤–ł–ľ—Ė—Ä—é—Ē—ā—Ć—Ā—Ź –≤ –ľ–Ķ—ā—Ä–į—Ö –∑–į —Ā–Ķ–ļ—É–Ĺ–ī—É ‚ÄĒ –ľ/—Ā. –£ —Ā–ł—Ā—ā–Ķ–ľ—Ė –°–ď–° –ĺ–ī–ł–Ĺ–ł—Ü–Ķ—é –≤–ł–ľ—Ė—Ä—é–≤–į–Ĺ–Ĺ—Ź —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė —Ē —Ā–į–Ĺ—ā–ł–ľ–Ķ—ā—Ä –∑–į —Ā–Ķ–ļ—É–Ĺ–ī—É ‚ÄĒ —Ā–ľ/—Ā. –£ –Ņ–ĺ–≤—Ā—Ź–ļ–ī–Ķ–Ĺ–Ĺ–ĺ–ľ—É –∂–ł—ā—ā—Ė –Ĺ–į–Ļ–Ņ—Ä–į–ļ—ā–ł—á–Ĺ—Ė—ą–ĺ—é –ĺ–ī–ł–Ĺ–ł—Ü–Ķ—é –≤–ł–ľ—Ė—Ä—é–≤–į–Ĺ–Ĺ—Ź —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė —Ē –ļ—Ė–Ľ–ĺ–ľ–Ķ—ā—Ä –Ĺ–į –≥–ĺ–ī–ł–Ĺ—É ‚ÄĒ –ļ–ľ/–≥–ĺ–ī. –£ –Ņ–Ķ–≤–Ĺ–ł—Ö –≥–į–Ľ—É–∑—Ź—Ö –Ľ—é–ī—Ā—Ć–ļ–ĺ—ó –ī—Ė—Ź–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ė —á–ł –ļ—Ä–į—ó–Ĺ–į—Ö –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—é—ā—Ć—Ā—Ź —Ā–Ņ–Ķ—Ü–ł—Ą—Ė—á–Ĺ—Ė –ĺ–ī–ł–Ĺ–ł—Ü—Ė —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė, —Ź–ļ-–ĺ—ā –≤—É–∑–ĺ–Ľ —á–ł —Ą—É—ā –∑–į —Ā–Ķ–ļ—É–Ĺ–ī—É.
–£ –Ĺ–į—É—Ü—Ė –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—Ē—ā—Ć—Ā—Ź —ā–į–ļ–ĺ–∂ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —É —ą–ł—Ä–ĺ–ļ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ė, —Ź–ļ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–ľ—Ė–Ĺ–ł –Ī—É–ī—Ć-—Ź–ļ–ĺ—ó –≤–Ķ–Ľ–ł—á–ł–Ĺ–ł (–Ĺ–Ķ –ĺ–Ī–ĺ–≤'—Ź–∑–ļ–ĺ–≤–ĺ —Ä–į–ī—Ė—É—Ā-–≤–Ķ–ļ—ā–ĺ—Ä–į ) –∑–į–Ľ–Ķ–∂–Ĺ–ĺ –≤—Ė–ī —Ė–Ĺ—ą–ĺ—ó (—á–į—Ā—ā—Ė—ą–Ķ –∑–ľ—Ė–Ĺ–ł –≤ —á–į—Ā—Ė, –į–Ľ–Ķ —ā–į–ļ–ĺ–∂ —É –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—Ė –į–Ī–ĺ –Ī—É–ī—Ć-—Ź–ļ–ĺ—ó —Ė–Ĺ—ą–ĺ—ó). –Ę–į–ļ, –Ĺ–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –≥–ĺ–≤–ĺ—Ä—Ź—ā—Ć –Ņ—Ä–ĺ –ļ—É—ā–ĺ–≤—É —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć , —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–ľ—Ė–Ĺ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ł , —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ö—Ė–ľ—Ė—á–Ĺ–ĺ—ó —Ä–Ķ–į–ļ—Ü—Ė—ó , –≥—Ä—É–Ņ–ĺ–≤—É —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć, —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –∑ ľ—Ē–ī–Ĺ–į–Ĺ–Ĺ—Ź —ā–ĺ—Č–ĺ. –ú–į—ā–Ķ–ľ–į—ā–ł—á–Ĺ–ĺ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—Ē—ā—Ć—Ā—Ź –Ņ–ĺ—Ö—Ė–ī–Ĺ–ĺ—é —Ą—É–Ĺ–ļ—Ü—Ė—ó .
–Ě–Ķ—Ö–į–Ļ —ā—Ė–Ľ–ĺ, —Č–ĺ –ľ–ĺ–∂–Ĺ–į –≤–≤–į–∂–į—ā–ł –∑–į –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ—É —ā–ĺ—á–ļ—É , —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź –Ņ–ĺ –ī–ĺ–≤—Ė–Ľ—Ć–Ĺ—Ė–Ļ —ā—Ä–į—Ē–ļ—ā–ĺ—Ä—Ė—ó . –®–Ľ—Ź—Ö, —Ź–ļ–ł–Ļ –Ņ—Ä–ĺ–Ļ—ą–Ľ–ĺ —ā—Ė–Ľ–ĺ –∑–į –Ņ—Ä–ĺ–ľ—Ė–∂–ĺ–ļ —á–į—Ā—É
Δ őĒ -->
t
{\displaystyle \Delta t}
Δ őĒ -->
s
=
s
(
t
+
Δ őĒ -->
t
)
− ‚ąí -->
s
(
t
)
{\displaystyle \Delta s=s(t+\Delta t)-s(t)}
–ó–į –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź–ľ:
v
=
Δ őĒ -->
s
Δ őĒ -->
t
{\displaystyle v={\frac {\Delta s}{\Delta t}}}
v
{\displaystyle v}
—Ā–Ķ—Ä–Ķ–ī–Ĺ—Ź —ą–Ľ—Ź—Ö–ĺ–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –į–Ī–ĺ —Ā–Ķ—Ä–Ķ–ī–Ĺ—Ē –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—ó –≤–Ķ–Ľ–ł—á–ł–Ĺ–ł —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –∑–į —á–į—Ā
Δ őĒ -->
t
{\displaystyle \Delta t}
v
=
s
t
,
{\displaystyle v={\frac {s}{t}},}
–ī–Ķ
s
{\displaystyle s}
t
{\displaystyle t}
–í–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ķ —ā–į–ļ–ł–ľ —Ā–Ņ–ĺ—Ā–ĺ–Ī–ĺ–ľ —Ā–Ķ—Ä–Ķ–ī–Ĺ—Ē –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ—ó –≤–Ķ–Ľ–ł—á–ł–Ĺ–ł —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė ‚ÄĒ —Ā–ļ–į–Ľ—Ź—Ä–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į —Ė –Ĺ–Ķ –Ņ–ĺ–≤ ľ—Ź–∑–į–Ĺ–į –∑ –Ņ–Ķ—Ä–Ķ–ľ—Ė—Č–Ķ–Ĺ–Ĺ—Ź–ľ —ā—Ė–Ľ–į. –Ě–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –ī—Ė–≤—á–ł–Ĺ–į, —Ź–ļ–į –Ņ—Ä–ĺ–Ī—Ė–≥–Ľ–į –ĺ–ī –ü–ĺ–Ľ—ā–į–≤–ł –ī–ĺ –•–ĺ—Ä–ĺ–Ľ–į , –į –Ņ–ĺ—ā—Ė–ľ –Ņ–ĺ–≤–Ķ—Ä–Ĺ—É–Ľ–į—Ā—Ź –Ĺ–į–∑–į–ī, –∑–ī—Ė–Ļ—Ā–Ĺ–ł–Ľ–į –Ĺ—É–Ľ—Ć–ĺ–≤–Ķ –Ņ–Ķ—Ä–Ķ–ľ—Ė—Č–Ķ–Ĺ–Ĺ—Ź, –ĺ–ī–Ĺ–į–ļ –≤–ĺ–Ĺ–į —Ä—É—Ö–į–Ľ–į—Ā—Ź –∑ –Ņ–Ķ–≤–Ĺ–ĺ—é —Ā–Ķ—Ä–Ķ–ī–Ĺ—Ć–ĺ—é —ą–≤–ł–ī–ļ—Ė—Ā—ā—é, —Ā–ļ–į–∂—Ė–ľ–ĺ 10 –ļ–ľ/–≥–ĺ–ī.
–ú–Ķ—Ö–į–Ĺ—Ė–ļ–į —É–∑–į–≥–į–Ľ—Ć–Ĺ—é—Ē –Ņ–ĺ–Ĺ—Ź—ā—ā—Ź ¬ę—ą–≤–ł–ī–ļ—Ė—Ā—ā—ƬĽ –ī–Ľ—Ź –ī–ĺ–≤—Ė–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä—É—Ö—É, –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—é—á–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ĺ–ł–Ļ –į–Ņ–į—Ä–į—ā –į–Ĺ–į–Ľ—Ė–∑—É . –ó–į–≥–į–Ľ–ĺ–ľ —ā—Ė–Ľ–į —Ä—É—Ö–į—é—ā—Ć—Ā—Ź –Ĺ–Ķ—Ä—Ė–≤–Ĺ–ĺ–ľ—Ė—Ä–Ĺ–ĺ –Ļ –ľ–ĺ–∂—É—ā—Ć –∑–ľ—Ė–Ĺ—é–≤–į—ā–ł –Ĺ–į–Ņ—Ä—Ź–ľ–ĺ–ļ —Ä—É—Ö—É. –Ē–Ľ—Ź –ĺ–Ņ–ł—Ā—É —ā–į–ļ–ĺ–≥–ĺ —Ä—É—Ö—É –≤–≤–ĺ–ī–ł—ā—Ć—Ā—Ź –Ņ–ĺ–Ĺ—Ź—ā—ā—Ź –ľ–ł—ā—ā—Ē–≤–ĺ—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė , —Ź–ļ—É –ľ–Ķ—Ö–į–Ĺ—Ė–ļ–į –Ĺ–į–ī–į–Ľ—Ė —Ė –Ĺ–į–∑–ł–≤–į—Ē –Ņ—Ä–ĺ—Ā—ā–ĺ —ą–≤–ł–ī–ļ—Ė—Ā—ā—é . –Ę—Ä–į—Ē–ļ—ā–ĺ—Ä—Ė—Ź —Ä—É—Ö—É —ā—Ė–Ľ–į —Ä–ĺ–∑–Ī–ł–≤–į—Ē—ā—Ć—Ā—Ź –Ĺ–į –ľ–į–Ľ–Ķ–Ĺ—Ć–ļ—Ė –ī—Ė–Ľ—Ź–Ĺ–ļ–ł, –Ĺ–į —Ź–ļ–ł—Ö —Ä—É—Ö –ľ–ĺ–∂–Ĺ–į –≤–≤–į–∂–į—ā–ł —Ä—Ė–≤–Ĺ–ĺ–ľ—Ė—Ä–Ĺ–ł–ľ —Ė –Ņ—Ä—Ź–ľ–ĺ–Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł–ľ, —Ė –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ĺ–į —Ü–ł—Ö –ī—Ė–Ľ—Ź–Ĺ–ļ–į—Ö. –®–≤–ł–ī–ļ—Ė—Ā—ā—Ć —ā—Ė–Ľ–į –≤ –ī–į–Ĺ—Ė–Ļ —ā–ĺ—á—Ü—Ė —ā—Ä–į—Ē–ļ—ā–ĺ—Ä—Ė—ó (—É –Ņ–Ķ–≤–Ĺ–ł–Ļ –ľ–ĺ–ľ–Ķ–Ĺ—ā —á–į—Ā—É) ‚ÄĒ –ľ–ł—ā—ā—Ē–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć , ‚ÄĒ –Ī—É–ī–Ķ —ā–ł–ľ —ā–ĺ—á–Ĺ—Ė—ą–Ķ –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–į –≤—Ė–ī–Ĺ–ĺ—ą–Ķ–Ĺ–Ĺ—Ź–ľ (1), —á–ł–ľ –ľ–Ķ–Ĺ—ą—Ė –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź
Δ őĒ -->
s
{\displaystyle \Delta s}
Δ őĒ -->
t
{\displaystyle \Delta t}
Δ őĒ -->
t
{\displaystyle \Delta t}
v
=
lim
Δ őĒ -->
t
→ ‚Üí -->
0
Δ őĒ -->
s
Δ őĒ -->
t
=
d
s
d
t
{\displaystyle v=\lim _{\Delta t\rightarrow 0}{\frac {\Delta s}{\Delta t}}={\frac {ds}{dt}}}
–ě—ā–∂–Ķ, –ľ–ł—ā—ā—Ē–≤—É —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –ľ–ĺ–∂–Ĺ–į –∑–Ĺ–į–Ļ—ā–ł –∑–į –∑–į–ī–į–Ĺ–ĺ—é –∑–į–Ľ–Ķ–∂–Ĺ—Ė—Ā—ā—é
s
(
t
)
{\displaystyle s(t)}
v
=
v
e
,
{\displaystyle \mathbf {v} =v\mathbf {e} ,}
–ī–Ķ
e
{\displaystyle \mathbf {e} }
–†–į–ī—Ė—É—Ā-–≤–Ķ–ļ—ā–ĺ—Ä–ł (—á–ĺ—Ä–Ĺ—Ė —Ā—ā—Ä—Ė–Ľ–ļ–ł). –í–Ķ–ļ—ā–ĺ—Ä–ł —Ā–Ķ—Ä–Ķ–ī–Ĺ—Ć–ĺ—ó —Ė –ľ–ł—ā—ā—Ē–≤–ł—Ö —ą–≤–ł–ī–ļ–ĺ—Ā—ā–Ķ–Ļ (–∑–Ķ–Ľ–Ķ–Ĺ—Ė —Ā—ā—Ä—Ė–Ľ–ļ–ł). –Ę—Ä–į—Ē–ļ—ā–ĺ—Ä—Ė—Ź (—á–Ķ—Ä–≤–ĺ–Ĺ–į –Ľ—Ė–Ĺ—Ė—Ź) –í–ł–ľ—Ė—Ä—é–≤–į–Ĺ–Ĺ—Ź –ľ–ł—ā—ā—Ē–≤–ĺ—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –į–≤—ā–ĺ–ľ–ĺ–Ī—Ė–Ľ—Ź –≤ –ļ–ľ/–≥–ĺ–ī –Į–ļ—Č–ĺ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—Ź –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –Ņ–ĺ—á–į—ā–ļ—É –≤—Ė–ī–Ľ—Ė–ļ—É –∑–į–ī–į—Ē—ā—Ć—Ā—Ź —Ä–į–ī—Ė—É—Ā–ĺ–ľ-–≤–Ķ–ļ—ā–ĺ—Ä–ĺ–ľ
r
{\displaystyle \mathbf {r} }
t
1
{\displaystyle t_{1}}
t
2
{\displaystyle t_{2}}
Δ őĒ -->
r
{\displaystyle \Delta \mathbf {r} }
–ó–į –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź–ľ, —Ā–Ķ—Ä–Ķ–ī–Ĺ—Ź —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –į–Ī–ĺ —Ā–Ķ—Ä–Ķ–ī–Ĺ—Ź —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ņ–Ķ—Ä–Ķ–ľ—Ė—Č–Ķ–Ĺ–Ĺ—Ź –ī–ĺ–≤—Ė–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ä—É—Ö—É –∑–į —Ė–Ĺ—ā–Ķ—Ä–≤–į–Ľ —á–į—Ā—É
Δ őĒ -->
t
{\displaystyle \Delta t}
[ 6] [ 7]
v
=
Δ őĒ -->
r
Δ őĒ -->
t
{\displaystyle \mathbf {v} ={\frac {\Delta \mathbf {r} }{\Delta t}}}
–ī–Ķ
Δ őĒ -->
r
{\displaystyle \Delta \mathbf {r} }
–Ņ–Ķ—Ä–Ķ–ľ—Ė—Č–Ķ–Ĺ–Ĺ—Ź —ā—Ė–Ľ–į –∑–į —á–į—Ā
Δ őĒ -->
t
{\displaystyle \Delta t}
–ü—Ė—Ā–Ľ—Ź –∑–į—Ā—ā–ĺ—Ā—É–≤–į–Ĺ–Ĺ—Ź –≥—Ä–į–Ĺ–ł—á–Ĺ–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī—É –≤–≤–ĺ–ī–ł—ā—Ć—Ā—Ź –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź –ľ–ł—ā—ā—Ē–≤–ĺ—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė.
–ú–ł—ā—ā—Ē–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ĺ–Ķ—Ä—Ė–≤–Ĺ–ĺ–ľ—Ė—Ä–Ĺ–ĺ–≥–ĺ —Ä—É—Ö—É ‚ÄĒ —Ü–Ķ –≤–Ķ–ļ—ā–ĺ—Ä —É —ā–ĺ—á—Ü—Ė, —Ź–ļ–ł–Ļ —Ē –≥—Ä–į–Ĺ–ł—Ü–Ķ—é —Ā–Ķ—Ä–Ķ–ī–Ĺ—Ė—Ö —ą–≤–ł–ī–ļ–ĺ—Ā—ā–Ķ–Ļ, –ļ–ĺ–Ľ–ł —Ė–Ĺ—ā–Ķ—Ä–≤–į–Ľ —á–į—Ā—É –Ņ—Ä—Ź–ľ—É—Ē –ī–ĺ –Ĺ—É–Ľ—Ź. –†–ĺ–∑–ļ—Ä–ł–≤–į—é—á–ł –ĺ–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź, —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć ‚ÄĒ —Ü–Ķ –≤—Ė–ī–Ĺ–ĺ—ą–Ķ–Ĺ–Ĺ—Ź –Ņ–Ķ—Ä–Ķ–ľ—Ė—Č–Ķ–Ĺ–Ĺ—Ź –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –∑–į —Ė–Ĺ—ā–Ķ—Ä–≤–į–Ľ —á–į—Ā—É, –ļ–ĺ–Ľ–ł —Ü–Ķ–Ļ —Ė–Ĺ—ā–Ķ—Ä–≤–į–Ľ –Ņ—Ä—Ź–ľ—É—Ē –ī–ĺ –Ĺ—É–Ľ—Ź, —ā–ĺ–Ī—ā–ĺ –Ņ–ĺ—Ö—Ė–ī–Ĺ–į –∑–į —á–į—Ā–ĺ–ľ –≤—Ė–ī —Ä–į–ī—Ė—É—Ā–į-–≤–Ķ–ļ—ā–ĺ—Ä–į
r
{\displaystyle \mathbf {r} }
v
=
lim
Δ őĒ -->
t
→ ‚Üí -->
0
Δ őĒ -->
r
Δ őĒ -->
t
=
d
r
d
t
=
r
˙ ňô -->
{\displaystyle \mathbf {v} =\lim _{\Delta t\rightarrow 0}{\frac {\Delta \mathbf {r} }{\Delta t}}={\frac {d\mathbf {r} }{dt}}={\dot {\mathbf {r} }}}
–í–Ķ–ļ—ā–ĺ—Ä —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė —Ā–Ņ—Ä—Ź–ľ–ĺ–≤–į–Ĺ–ł–Ļ —É –Ī—Ė–ļ —Ä—É—Ö—É —ā–ĺ—á–ļ–ł –Ņ–ĺ –ī–ĺ—ā–ł—á–Ĺ—Ė–Ļ –ī–ĺ —ā—Ä–į—Ē–ļ—ā–ĺ—Ä—Ė—ó —ó—ó —Ä—É—Ö—É.
–Ę–į–ļ —Ā–į–ľ–ĺ, –Ņ–ĺ—Ö—Ė–ī–Ĺ–į –≤—Ė–ī —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –ī–į—Ē –ľ–ł—ā—ā—Ē–≤–Ķ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź —ā—Ė–Ľ–į –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā —á–į—Ā—É
t
{\displaystyle t}
a
=
d
v
d
t
=
d
2
r
d
t
2
=
r
¨ ¬® -->
{\displaystyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {r} }{dt^{2}}}={\ddot {\mathbf {r} }}}
–ü—Ä–ĺ—Ē–ļ—Ü—Ė—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –Ĺ–į –ĺ—Ā—Ė –Ņ—Ä—Ź–ľ–ĺ–ļ—É—ā–Ĺ–ĺ—ó –ī–Ķ–ļ–į—Ä—ā–ĺ–≤–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ī–ĺ—Ä—Ė–≤–Ĺ—é—é—ā—Ć –Ņ–Ķ—Ä—ą–ł–ľ –Ņ–ĺ—Ö—Ė–ī–Ĺ–ł–ľ –∑–į —á–į—Ā–ĺ–ľ –≤—Ė–ī –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ł—Ö –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —ā–ĺ—á–ļ–ł, —Č–ĺ —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź:
v
x
=
x
˙ ňô -->
;
v
y
=
y
˙ ňô -->
;
v
z
=
z
˙ ňô -->
.
{\displaystyle v_{x}={\dot {x}};v_{y}={\dot {y}};v_{z}={\dot {z}}.}
–ó —Ü—Ć–ĺ–≥–ĺ:
v
=
x
˙ ňô -->
i
+
y
˙ ňô -->
j
+
z
˙ ňô -->
k
{\displaystyle \mathbf {v} ={\dot {x}}\mathbf {i} +{\dot {y}}\mathbf {j} +{\dot {z}}\mathbf {k} }
v
=
x
˙ ňô -->
2
+
y
˙ ňô -->
2
+
z
˙ ňô -->
2
{\displaystyle v={\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}}}}
–£ —Ü–ł–Ľ—Ė–Ĺ–ī—Ä–ł—á–Ĺ—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā
v
=
ρ ŌĀ -->
˙ ňô -->
2
+
(
ρ ŌĀ -->
φ ŌÜ -->
˙ ňô -->
)
2
+
z
˙ ňô -->
2
;
{\displaystyle v={\sqrt {{\dot {\rho }}^{2}+(\rho {\dot {\varphi }})^{2}+{\dot {z}}^{2}}};}
—Ė —É —Ā—Ą–Ķ—Ä–ł—á–Ĺ—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā
v
=
r
˙ ňô -->
2
+
(
r
θ őł -->
˙ ňô -->
)
2
+
(
r
φ ŌÜ -->
˙ ňô -->
sin
‚Ā° -->
θ őł -->
)
2
.
{\displaystyle v={\sqrt {{\dot {r}}^{2}+(r{\dot {\theta }})^{2}+(r{\dot {\varphi }}\sin {\theta })^{2}}}.}
–ö—Ė–Ĺ—Ü–Ķ–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
f
{\displaystyle v_{f}}
v
i
{\displaystyle v_{i}}
–Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź–ľ
a
{\displaystyle a}
t
{\displaystyle t}
v
f
=
v
i
+
a
t
{\displaystyle v_{f}=v_{i}+at\,}
–°–Ķ—Ä–Ķ–ī–Ĺ—Ź —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –ĺ–Ī ľ—Ē–ļ—ā–į –∑ –Ņ–ĺ—Ā—ā—Ė–Ļ–Ĺ–ł–ľ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź–ľ —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć
(
v
i
+
v
f
)
2
{\displaystyle {\frac {(v_{i}+v_{f})}{2}}}
s
{\displaystyle s}
t
{\displaystyle t}
s
=
t
× √ó -->
(
v
i
+
v
f
)
2
{\displaystyle s=t\times {\frac {(v_{i}+v_{f})}{2}}\,}
–Į–ļ—Č–ĺ –≤—Ė–ī–ĺ–ľ–į —ā—Ė–Ľ—Ć–ļ–ł –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć, –ľ–ĺ–∂–Ĺ–į –∑–į—Ā—ā–ĺ—Ā–ĺ–≤—É–≤–į—ā–ł —Ą–ĺ—Ä–ľ—É–Ľ—É:
s
=
v
i
t
+
(
a
t
2
)
2
{\displaystyle s=v_{i}t+{\frac {(at^{2})}{2}}\,}
–ó —Ü–ł—Ö –Ī–į–∑–ĺ–≤–ł—Ö —Ä—Ė–≤–Ĺ—Ź–Ĺ—Ć –≤–ł–≤–ĺ–ī–ł—ā—Ć—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–į, –Ĺ–Ķ –∑–į–Ľ–Ķ–∂–Ĺ–į –≤—Ė–ī –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—É —á–į—Ā—É
t
{\displaystyle t}
v
f
2
=
v
i
2
+
2
a
s
{\displaystyle v_{f}^{2}=v_{i}^{2}+2as\,}
–Ě–į–≤–Ķ–ī–Ķ–Ĺ—Ė —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤—Ė —Ź–ļ –ī–Ľ—Ź –ļ–Ľ–į—Ā–ł—á–Ĺ–ĺ—ó –ľ–Ķ—Ö–į–Ĺ—Ė–ļ–ł , —ā–į–ļ —Ė –ī–Ľ—Ź —Ā–Ņ–Ķ—Ü—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–Ķ–ĺ—Ä—Ė—ó –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė . –í—Ė–ī–ľ—Ė–Ĺ–Ĺ—Ė—Ā—ā—Ć —Ā–ł—ā—É–į—Ü—Ė—ó –Ņ–ĺ–Ľ—Ź–≥–į—Ē, –∑–ĺ–ļ—Ä–Ķ–ľ–į, —É —ā–ĺ–ľ—É, —Č–ĺ –≤ –ļ–Ľ–į—Ā–ł—á–Ĺ—Ė–Ļ –ľ–Ķ—Ö–į–Ĺ—Ė—Ü—Ė –ī–Ľ—Ź –≤—Ā—Ė—Ö —Ā–Ņ–ĺ—Ā—ā–Ķ—Ä—Ė–≥–į—á—Ė–≤ –≤ —Ė–Ĺ–Ķ—Ä—Ü—Ė–Ļ–Ĺ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö –≤—Ė–ī–Ľ—Ė–ļ—É –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź —ā—Ė–Ľ–į, —Č–ĺ —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź, –Ī—É–ī–Ķ –ĺ–ī–Ĺ–į–ļ–ĺ–≤–ł–ľ. –Ē–Ľ—Ź —Ā–Ņ–Ķ—Ü—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–Ķ–ĺ—Ä—Ė—ó –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė —Ü–Ķ –Ĺ–Ķ —ā–į–ļ.
–†—É—Ö –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –Ņ–ĺ –ļ–ĺ–Ľ—É –ľ–ĺ–∂–Ĺ–į –ĺ—Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É–≤–į—ā–ł —Ź–ļ –Ľ—Ė–Ĺ—Ė–Ļ–Ĺ–ł–ľ–ł –ļ—Ė–Ĺ–Ķ–ľ–į—ā–ł—á–Ĺ–ł–ľ–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ–į–ľ–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤—Ė –≤–ł–ļ–Ľ–į–ī–ĺ–ļ, –∑—Ä–ĺ–Ī–Ľ–Ķ–Ĺ–ł—Ö –≤–ł—Č–Ķ, —ā–į–ļ —Ė –ļ—É—ā–ĺ–≤–ł–ľ–ł –ļ—Ė–Ĺ–Ķ–ľ–į—ā–ł—á–Ĺ–ł–ľ–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ–į–ľ–ł ‚ÄĒ –ļ—É—ā–ĺ–≤–ĺ—é –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ĺ—é
φ ŌÜ -->
{\displaystyle \varphi }
ω ŌČ -->
{\displaystyle \omega }
–ü—Ä–ł –ĺ–Ī–Ķ—Ä—ā–į–Ĺ–Ĺ—Ė –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –∑ –ļ—É—ā–ĺ–≤–ĺ—é —ą–≤–ł–ī–ļ—Ė—Ā—ā—é
ω ŌČ -->
=
φ ŌÜ -->
˙ ňô -->
{\displaystyle \omega ={\dot {\varphi }}}
–ļ–ĺ–Ľ—É —Ä–į–ī—Ė—É—Ā–ĺ–ľ R —ó—ó –ľ–ł—ā—ā—Ē–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ĺ—é
v
=
ω ŌČ -->
R
=
φ ŌÜ -->
˙ ňô -->
R
,
{\displaystyle v=\omega R={\dot {\varphi }}R,}
–†—É—Ö —ā–ĺ—á–ļ–ł –≤ –Ņ–Ľ–ĺ—Č–ł–Ĺ—Ė —É –Ņ–ĺ–Ľ—Ź—Ä–Ĺ—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ó–į–≥–į–Ľ–ĺ–ľ, —Ź–ļ—Č–ĺ —Ä–ĺ–∑–≥–Ľ—Ź–ī–į—ā–ł —Ä—É—Ö –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł A –≤ –Ņ–Ľ–ĺ—Č–ł–Ĺ—Ė –≤ –Ņ–ĺ–Ľ—Ź—Ä–Ĺ—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā , —ā–ĺ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –ľ–ĺ–∂–Ĺ–į —Ä–ĺ–∑–ļ–Ľ–į—Ā—ā–ł –Ĺ–į –ī–≤—Ė –≤–∑–į—Ē–ľ–Ĺ–ĺ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—Ė —Ā–ļ–Ľ–į–ī–ĺ–≤—Ė: —Ä–į–ī—Ė–į–Ľ—Ć–Ĺ—É (–Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ķ–≤—É) –Ļ —ā–į–Ĺ–≥–Ķ–Ĺ—Ü—Ė–į–Ľ—Ć–Ĺ—É (—ā—Ä–į–Ĺ—Ā–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ—É). –†–į–ī—Ė–į–Ľ—Ć–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
r
{\displaystyle \mathbf {v} _{r}}
—Ä–į–ī—Ė—É—Ā-–≤–Ķ–ļ—ā–ĺ—Ä–į —ā–ĺ—á–ļ–ł –Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—Ē –≤—Ė–ī–ī–į–Ľ–Ķ–Ĺ–Ĺ—Ź –į–Ī–ĺ –Ĺ–į–Ī–Ľ–ł–∂–Ķ–Ĺ–Ĺ—Ź —ā–ĺ—á–ļ–ł A –ī–ĺ –Ņ–ĺ—á–į—ā–ļ—É —Ā–ł—Ā—ā–Ķ–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā O . –Ę–į–Ĺ–≥–Ķ–Ĺ—Ü—Ė–į–Ľ—Ć–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
φ ŌÜ -->
{\displaystyle \mathbf {v} _{\varphi }}
–ź –Ĺ–į–≤–ļ–ĺ–Ľ–ĺ –Ņ–ĺ—á–į—ā–ļ—É –≤—Ė–ī–Ľ—Ė–ļ—É –ě —Ā–ł—Ā—ā–Ķ–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā:
v
=
v
r
+
v
φ ŌÜ -->
,
{\displaystyle \mathbf {v} =\mathbf {v} _{r}+\mathbf {v} _{\varphi },}
–Ņ—Ä–ł—á–ĺ–ľ—É
v
r
=
r
˙ ňô -->
r
r
;
v
φ ŌÜ -->
=
φ ŌÜ -->
˙ ňô -->
(
k
× √ó -->
r
)
,
{\displaystyle \mathbf {v} _{r}={\frac {\dot {r}}{r}}\mathbf {r} ;\mathbf {v} _{\varphi }={\dot {\varphi }}(\mathbf {k} \times r),}
–ī–Ķ
r
{\displaystyle \mathbf {r} }
k
{\displaystyle \mathbf {k} }
r
{\displaystyle \mathbf {r} }
φ ŌÜ -->
{\displaystyle \varphi }
r
{\displaystyle \mathbf {r} }
φ ŌÜ -->
{\displaystyle \varphi }
v
r
=
r
˙ ňô -->
;
v
φ ŌÜ -->
=
r
φ ŌÜ -->
˙ ňô -->
.
{\displaystyle v_{r}={\dot {r}};v_{\varphi }=r{\dot {\varphi }}.}
–ü–ĺ–≤–Ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –≤ —Ü—Ć–ĺ–ľ—É —Ä–į–∑—Ė:
v
=
v
r
2
+
v
φ ŌÜ -->
2
.
{\displaystyle v={\sqrt {v_{r}^{2}+v_{\varphi }^{2}}}.}
–ó–į–≥–į–Ľ—Ć–Ĺ–ł–Ļ –≤–ł–Ņ–į–ī–ĺ–ļ —Ä—É—Ö—É —ā–≤–Ķ—Ä–ī–ĺ–≥–ĺ —ā—Ė–Ľ–į
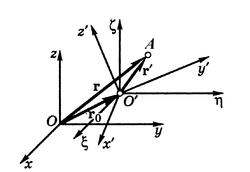
–ó–į–≥–į–Ľ–ĺ–ľ –≤—Ė–Ľ—Ć–Ĺ–Ķ —ā–≤–Ķ—Ä–ī–Ķ —ā—Ė–Ľ–ĺ –ľ–į—Ē —ą—Ė—Ā—ā—Ć —Ā—ā—É–Ņ–Ķ–Ĺ—Ė–≤ –≤—Ė–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ė . –ô–ĺ–≥–ĺ —Ä–ĺ–∑—ā–į—ą—É–≤–į–Ĺ–Ĺ—Ź –≤ –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—Ė –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź —ā—Ä—Ć–ĺ–ľ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į–ľ–ł
x
0
,
y
0
,
z
0
{\displaystyle x_{0},y_{0},z_{0}}
–Ņ–ĺ–Ľ—é—Ā–ĺ–ľ , —Ė —ā—Ä—Ć–ĺ–ľ–į –ļ—É—ā–į–ľ–ł –ē–Ļ–Ľ–Ķ—Ä–į Ōą, őł, ŌÜ , —Ź–ļ—Ė —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—é—ā—Ć –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—Ź —ā—Ė–Ľ–į –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –Ņ—Ä—Ź–ľ–ĺ–ļ—É—ā–Ĺ–ĺ—ó –ī–Ķ–ļ–į—Ä—ā–ĺ–≤–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā O'őĺő∑Ōā , –ĺ—Ā—Ė —Ź–ļ–ĺ—ó –Ņ–į—Ä–į–Ľ–Ķ–Ľ—Ć–Ĺ—Ė –ī–ĺ –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ł—Ö –ĺ—Ā–Ķ–Ļ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ—ó (–Ĺ–Ķ—Ä—É—Ö–ĺ–ľ–ĺ—ó) —Ā–ł—Ā—ā–Ķ–ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā Oxyz , –į –Ņ–ĺ—á–į—ā–ĺ–ļ –∑–Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –≤ –Ņ–ĺ–Ľ—é—Ā—Ė O'. –í—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ĺ —Ä—É—Ö —ā—Ė–Ľ–į –ľ–ĺ–∂–Ĺ–į —Ä–ĺ–∑–≥–Ľ—Ź–ī–į—ā–ł —Ź–ļ —Ā—É–ļ—É–Ņ–Ĺ—Ė—Ā—ā—Ć –ī–≤–ĺ—Ö —Ä—É—Ö—Ė–≤, —Č–ĺ –≤—Ė–ī–Ī—É–≤–į—é—ā—Ć—Ā—Ź –ĺ–ī–Ĺ–ĺ—á–į—Ā–Ĺ–ĺ ‚ÄĒ –Ņ–ĺ—Ā—ā—É–Ņ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑—Ė —ą–≤–ł–ī–ļ—Ė—Ā—ā—é
v
O
=
d
r
O
d
t
{\displaystyle v_{O}={\frac {dr_{O}}{dt}}}
–ĺ–Ī–Ķ—Ä—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ĺ–į–≤–ļ–ĺ–Ľ–ĺ –Ņ–ĺ–Ľ—é—Ā–į –∑ –ļ—É—ā–ĺ–≤–ĺ—é —ą–≤–ł–ī–ļ—Ė—Ā—ā—é ŌČ , —Ź–ļ–į –Ĺ–Ķ –∑–į–Ľ–Ķ–∂–ł—ā—Ć –≤—Ė–ī –≤–ł–Ī–ĺ—Ä—É –Ņ–ĺ–Ľ—é—Ā–į.
–Ě–į —Ä–ł—Ā—É–Ĺ–ļ—É –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –∂–ĺ—Ä—Ā—ā–ļ–ĺ –∑–≤ ľ—Ź–∑–į–Ĺ—É –∑ —ā—Ė–Ľ–ĺ–ľ —Ä—É—Ö–ĺ–ľ—É —Ā–ł—Ā—ā–Ķ–ľ—É –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā O'x'y'z' . –†–į–ī—Ė—É—Ā–ł-–≤–Ķ–ļ—ā–ĺ—Ä–ł –ī–ĺ–≤—Ė–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł A —ā—Ė–Ľ–į –≤ –Ĺ–Ķ—Ä—É—Ö–ĺ–ľ—Ė–Ļ —Ė —Ä—É—Ö–ĺ–ľ—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ–į—Ö –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ņ–ĺ–≤ ľ—Ź–∑–į–Ĺ—Ė —Ā–Ņ—Ė–≤–≤—Ė–ī–Ĺ–ĺ—ą–Ķ–Ĺ–Ĺ—Ź–ľ:
r
=
r
O
+
r
′
.
{\displaystyle \mathbf {r} =\mathbf {r_{O}} +\mathbf {r'} .}
–®–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
{\displaystyle \mathbf {v} }
A —ā—Ė–Ľ–į –Ī—É–ī–Ķ –ī–ĺ—Ä—Ė–≤–Ĺ—é–≤–į—ā–ł:
v
=
d
r
O
d
t
+
d
r
′
d
t
=
v
O
+
ω ŌČ -->
× √ó -->
r
′
,
{\displaystyle \mathbf {v} ={\frac {d\mathbf {r_{O}} }{dt}}+{\frac {d\mathbf {r'} }{dt}}=\mathbf {v_{O}} +{\boldsymbol {\omega }}\times \mathbf {r'} ,}
–ī–Ķ
v
0
=
d
r
O
d
t
{\displaystyle \mathbf {v_{0}} ={\frac {d\mathbf {r_{O}} }{dt}}}
–ó–≤ ľ—Ź–∑–ĺ–ļ –ľ—Ė–∂ —Ä–į–ī—Ė—É—Ā–į–ľ–ł-–≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł
r
{\displaystyle \mathbf {r} }
r
′
{\displaystyle \mathbf {r'} }
A , —Č–ĺ —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–ľ–ł –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–Ĺ–ĺ –∑ –Ņ–ĺ—á–į—ā–ļ—É O –Ĺ–Ķ—Ä—É—Ö–ĺ–ľ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –≤—Ė–ī–Ľ—Ė–ļ—É (x, y, z ) —Ė –Ņ–ĺ—á–į—ā–ļ—É O' —Ä—É—Ö–ĺ–ľ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł (x', y', z'), –ľ–į—Ē –≤–ł–≥–Ľ—Ź–ī:
r
=
r
O
+
r
′
=
r
O
+
(
x
′
i
′
+
y
′
j
′
+
z
′
k
′
)
,
{\displaystyle \mathbf {r} =\mathbf {r_{O}} +\mathbf {r'} =\mathbf {r_{O}} +\left(x'\mathbf {i'} +y'\mathbf {j'} +z'\mathbf {k'} \right),}
–ī–Ķ x', y', z' ‚ÄĒ –Ņ—Ä–ĺ—Ē–ļ—Ü—Ė—ó
r
′
{\displaystyle \mathbf {r'} }
i
′
,
j
′
,
k
′
{\displaystyle \mathbf {i'} ,\mathbf {j'} ,\mathbf {k'} }
–ź–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
a
{\displaystyle \mathbf {v_{a}} }
A
(
r
)
{\displaystyle A(\mathbf {r} )}
v
a
=
d
r
d
t
=
d
r
O
d
t
+
x
′
d
i
′
d
t
+
y
′
d
j
′
d
t
+
z
′
d
k
′
d
t
+
d
x
′
d
t
i
′
+
d
y
′
d
t
j
′
+
d
z
′
d
t
k
′
{\displaystyle \mathbf {v_{a}} ={\frac {d\mathbf {r} }{dt}}={\frac {d\mathbf {r_{O}} }{dt}}+x'{\frac {d\mathbf {i'} }{dt}}+y'{\frac {d\mathbf {j'} }{dt}}+z'{\frac {d\mathbf {k'} }{dt}}+{\frac {dx'}{dt}}\mathbf {i'} +{\frac {dy'}{dt}}\mathbf {j'} +{\frac {dz'}{dt}}\mathbf {k'} }
–£ —Ü—Ć–ĺ–ľ—É —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ė:
–Ņ–Ķ—Ä—ą–ł–Ļ –ī–ĺ–ī–į–Ĺ–ĺ–ļ
d
r
O
d
t
=
v
0
{\displaystyle {\frac {d\mathbf {r_{O}} }{dt}}=\mathbf {v_{0}} }
–Ĺ–į—Ā—ā—É–Ņ–Ĺ—Ė —ā—Ä–ł –ī–ĺ–ī–į–Ĺ–ļ–ł –ĺ–Ņ–ł—Ā—É—é—ā—Ć –∑–ľ—Ė–Ĺ—É –≤ —á–į—Ā—Ė –ĺ—Ä—ā—Ė–≤
i
′
,
j
′
,
k
′
{\displaystyle \mathbf {i',j',k'} }
ŌČ:
i
′
d
t
=
ω ŌČ -->
× √ó -->
i
′
;
j
′
d
t
=
ω ŌČ -->
× √ó -->
j
′
;
k
′
d
t
=
ω ŌČ -->
× √ó -->
k
′
{\displaystyle {\frac {\mathbf {i'} }{dt}}=\omega \times \mathbf {i'} ;{\frac {\mathbf {j'} }{dt}}=\omega \times \mathbf {j'} ;{\frac {\mathbf {k'} }{dt}}=\omega \times \mathbf {k'} }
–ĺ—Ā—ā–į–Ĺ–Ĺ—Ė —ā—Ä–ł –ī–ĺ–ī–į–Ĺ–ļ–ł —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—é—ā—Ć –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ—É —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
r
{\displaystyle \mathbf {v_{r}} }
A
(
r
′
)
{\displaystyle A(\mathbf {r'} )}
–ě—ā–∂–Ķ,
v
a
=
v
0
+
ω ŌČ -->
× √ó -->
r
′
+
v
r
,
{\displaystyle \mathbf {v_{a}} =\mathbf {v_{0}} +\mathbf {\omega \times r'} +\mathbf {v_{r}} ,}
v
e
=
v
0
+
ω ŌČ -->
× √ó -->
r
′
{\displaystyle \mathbf {v_{e}} =\mathbf {v_{0}} +\mathbf {\omega \times r'} }
—ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —ā–ĺ—á–ļ–ł A , —Č–ĺ –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—Ė–Ļ —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė —ā—Ė—Ē—ó –Ĺ–Ķ–∑–ľ—Ė–Ĺ–Ĺ–ĺ –Ņ–ĺ–≤ ľ—Ź–∑–į–Ĺ–ĺ—ó –∑ —Ä—É—Ö–ĺ–ľ–ĺ—é —Ā–ł—Ā—ā–Ķ–ľ–ĺ—é –≤—Ė–ī–Ľ—Ė–ļ—É —ā–ĺ—á–ļ–ł –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—É, –∑ —Ź–ļ–ĺ—é –Ĺ–į—Ä–į–∑—Ė –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź —ā–ĺ—á–ļ–į A , —Č–ĺ —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź.
–ě—ā–∂–Ķ, –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ä—É—Ö—É —ā–ĺ—á–ļ–ł –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ—Ė–Ļ —Ā—É–ľ—Ė —ó—ó –Ņ–Ķ—Ä–Ķ–Ĺ–ĺ—Ā–Ĺ–ĺ—ó —Ė –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā–Ķ–Ļ:
v
a
=
v
e
+
v
r
{\displaystyle \mathbf {v_{a}} =\mathbf {v_{e}} +\mathbf {v_{r}} }
–¶–Ķ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—Ź, –Ĺ–į —Ź–ļ–ĺ–ľ—É –Ī–į–∑—É—Ē—ā—Ć—Ā—Ź –Ņ–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –ď–į–Ľ—Ė–Ľ–Ķ—Ź , —Ē —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ł–ľ —É –ļ–Ľ–į—Ā–ł—á–Ĺ—Ė–Ļ –ľ–Ķ—Ö–į–Ĺ—Ė—Ü—Ė , –į–Ľ–Ķ –Ņ–ĺ—ā—Ä–Ķ–Ī—É—Ē —É—ā–ĺ—á–Ĺ–Ķ–Ĺ–Ĺ—Ź –≤ —Ä–Ķ–Ľ—Ź—ā–ł–≤—Ė—Ā—ā—Ā—Ć–ļ—Ė–Ļ –ľ–Ķ—Ö–į–Ĺ—Ė—Ü—Ė , –ī–Ķ –ī–Ľ—Ź —Ü—Ć–ĺ–≥–ĺ –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—Ē—ā—Ć—Ā—Ź –Ņ–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź –õ–ĺ—Ä–Ķ–Ĺ—Ü–į .
–£ –ľ–Ķ—Ö–į–Ĺ—Ė—Ü—Ė –õ–į–≥—Ä–į–Ĺ–∂–į –į–Ĺ–į–Ľ–ĺ–≥—Ė—á–Ĺ–ł–ľ —á–ł–Ĺ–ĺ–ľ –≤–≤–ĺ–ī–ł—ā—Ć—Ā—Ź —É–∑–į–≥–į–Ľ—Ć–Ĺ–Ķ–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć :
q
˙ ňô -->
=
d
q
d
t
{\displaystyle {\dot {q}}={\frac {dq}{dt}}}
–ī–Ķ
q
{\displaystyle q}
—É–∑–į–≥–į–Ľ—Ć–Ĺ–Ķ–Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į , —ā–ĺ–Ī—ā–ĺ –ĺ–ī–Ĺ–į –∑ –≤–Ķ–Ľ–ł—á–ł–Ĺ, —Č–ĺ –≤–ł–∑–Ĺ–į—á–į—é—ā—Ć –ľ–ł—ā—ā—Ē–≤–Ķ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—Ź –ľ–Ķ—Ö–į–Ĺ—Ė—á–Ĺ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł.
–Ě–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –Ņ—Ä–ł –ĺ–Ī–Ķ—Ä—ā–į–Ĺ–Ĺ—Ė —ā–≤–Ķ—Ä–ī–ĺ–≥–ĺ —ā—Ė–Ľ–į, —É–∑–į–≥–į–Ľ—Ć–Ĺ–Ķ–Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į: –ļ—É—ā –Ņ–ĺ–≤–ĺ—Ä–ĺ—ā—É
φ ŌÜ -->
{\displaystyle \varphi }
–ļ—É—ā–ĺ–≤–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć :
ω ŌČ -->
=
d
φ ŌÜ -->
d
t
{\displaystyle \omega ={\frac {d\varphi }{dt}}}
–ě—Ā–Ĺ–ĺ–≤–Ĺ–ł–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā —ā–Ķ–ĺ—Ä—Ė—ó –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė –≤—Ā—ā–į–Ĺ–ĺ–≤–Ľ—é—Ē –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ—É —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć, –∑ —Ź–ļ–ĺ—é –ľ–ĺ–∂–Ķ –Ņ–Ķ—Ä–Ķ–ī–į–≤–į—ā–ł—Ā—Ć —Ė–Ĺ—Ą–ĺ—Ä–ľ–į—Ü—Ė—Ź , –į, –ĺ—ā–∂–Ķ, —Ė —Ä—É—Ö–į—ā–ł—Ā—Ź —ā—Ė–Ľ–ĺ. –¶—Ź –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć ‚ÄĒ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ā–≤—Ė—ā–Ľ–į (–ľ–į—Ē—ā—Ć—Ā—Ź –Ĺ–į —É–≤–į–∑—Ė —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ā–≤—Ė—ā–Ľ–į —É –≤–į–ļ—É—É–ľ—Ė) ‚ÄĒ —Ē —É–Ĺ—Ė–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ–ĺ—é —Ą—Ė–∑–ł—á–Ĺ–ĺ—é —Ā—ā–į–Ľ–ĺ—é .
–Ē–Ľ—Ź –ĺ–Ņ–ł—Ā—É —Ä—É—Ö—É —ā—Ė–Ľ —É —ā–Ķ–ĺ—Ä—Ė—ó –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė –≤–≤–ĺ–ī–ł—ā—Ć—Ā—Ź 4-–≤–Ķ–ļ—ā–ĺ—Ä —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė, –į–Ī–ĺ 4-—ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
u
i
=
d
x
i
d
s
{\displaystyle u^{i}={\frac {dx^{i}}{ds}}}
–ī–Ķ ds ‚ÄĒ –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä–ĺ–≤–ĺ-—á–į—Ā–ĺ–≤–ł–Ļ —Ė–Ĺ—ā–Ķ—Ä–≤–į–Ľ :
u
i
=
(
1
1
− ‚ąí -->
v
2
/
c
2
,
v
c
1
− ‚ąí -->
v
2
/
c
2
)
{\displaystyle u^{i}=\left({\frac {1}{\sqrt {1-v^{2}/c^{2}}}},{\frac {\mathbf {v} }{c{\sqrt {1-v^{2}/c^{2}}}}}\right)}
–ī–Ķ
v
{\displaystyle \mathbf {v} }
—ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ā–≤—Ė—ā–Ľ–į —É –≤–į–ļ—É—É–ľ—Ė.
4-—ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć ‚ÄĒ –Ī–Ķ–∑—Ä–ĺ–∑–ľ—Ė—Ä–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į. –Ē–Ľ—Ź 4-–≤–Ķ–ļ—ā–ĺ—Ä–į —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –∑–į–≤–∂–ī–ł —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–Ķ —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź:
u
i
u
i
=
1
{\displaystyle u^{i}u_{i}=1\;}
–ó–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė —ā—Ė–Ľ–į –∑–į–Ľ–Ķ–∂–ł—ā—Ć –≤—Ė–ī —Ā–ł—Ā—ā–Ķ–ľ–ł –≤—Ė–ī–Ľ—Ė–ļ—É —Ā–Ņ–ĺ—Ā—ā–Ķ—Ä—Ė–≥–į—á–į . –£ –ļ–Ľ–į—Ā–ł—á–Ĺ—Ė–Ļ –ľ–Ķ—Ö–į–Ĺ—Ė—Ü—Ė , —Ź–ļ–į –≤–ł–ļ–ĺ—Ä–ł—Ā—ā–ĺ–≤—É—Ē –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –ď–į–Ľ—Ė–Ľ–Ķ—Ź , —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —ā—Ė–Ľ–į –≤ –Ĺ–ĺ–≤—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –≤—Ė–ī–Ľ—Ė–ļ—É —Ē –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ—é —Ä—Ė–∑–Ĺ–ł—Ü–Ķ—é –Ļ–ĺ–≥–ĺ —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –≤ —Ā—ā–į—Ä—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –Ļ —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –Ĺ–ĺ–≤–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –≤—Ė–ī–Ľ—Ė–ļ—É –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ —Ā—ā–į—Ä–ĺ—ó :
v
′ ‚Ä≤ -->
=
v
− ‚ąí -->
V
{\displaystyle \mathbf {v} ^{\prime }=\mathbf {v} -\mathbf {V} }
–ī–Ķ
v
′ ‚Ä≤ -->
{\displaystyle \mathbf {v} ^{\prime }}
v
{\displaystyle \mathbf {v} }
V
{\displaystyle \mathbf {V} }
–£ —Ā–ł—Ā—ā–Ķ–ľ—Ė –≤—Ė–ī–Ľ—Ė–ļ—É, —Ź–ļ–į —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź –∑ —ā—Ė—Ē—é —Ā–į–ľ–ĺ—é —ą–≤–ł–ī–ļ—Ė—Ā—ā—é, —Č–ĺ –Ļ —ā—Ė–Ľ–ĺ, –≤–ĺ–Ĺ–ĺ —Ē –Ĺ–Ķ–Ņ–ĺ—Ä—É—ą–Ĺ–ł–ľ.
–£ —ā–Ķ–ĺ—Ä—Ė—ó –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ—Ā—ā—Ė –Ĺ–į–≤–Ķ–ī–Ķ–Ĺ–į —Ą–ĺ—Ä–ľ—É–Ľ–į –Ĺ–Ķ —Ē —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ—é, –ĺ—Ā–ļ—Ė–Ľ—Ć–ļ–ł –∂–ĺ–ī–Ĺ–Ķ —ā—Ė–Ľ–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ —Ä—É—Ö–į—ā–ł—Ā—Ź –∑—Ė —ą–≤–ł–ī–ļ—Ė—Ā—ā—é, —Ź–ļ–į –Ņ–Ķ—Ä–Ķ–≤–ł—Č—É–≤–į–Ľ–į –Ī —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ā–≤—Ė—ā–Ľ–į. –Ě–į–Ņ—Ä–ł–ļ–Ľ–į–ī, —É —Ä–į–∑—Ė, –ļ–ĺ–Ľ–ł –Ĺ–į–Ņ—Ä—Ź–ľ —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –Ĺ–ĺ–≤–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –≤—Ė–ī–Ľ—Ė–ļ—É –∑–Ī—Ė–≥–į—Ē—ā—Ć—Ā—Ź –∑ –Ĺ–į–Ņ—Ä—Ź–ľ–ļ–ĺ–ľ —Ä—É—Ö—É —ā—Ė–Ľ–į, —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —É –Ĺ–ĺ–≤—Ė–Ļ —Ā–ł—Ā—ā–Ķ–ľ—Ė –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē
v
′ ‚Ä≤ -->
=
v
− ‚ąí -->
V
1
− ‚ąí -->
v
V
/
c
2
{\displaystyle v^{\prime }={\frac {v-V}{1-vV/c^{2}}}}
–ó–į –ľ–į–Ľ–ł—Ö —ą–≤–ł–ī–ļ–ĺ—Ā—ā–Ķ–Ļ
v
≪ ‚Č™ -->
c
{\displaystyle v\ll c}
V
≪ ‚Č™ -->
c
{\displaystyle V\ll c}
–Ņ–Ķ—Ä–Ķ—ā–≤–ĺ—Ä–Ķ–Ĺ—Ć –ď–į–Ľ—Ė–Ľ–Ķ—Ź .
–Ę—Ė–Ľ–ĺ, —Ź–ļ–Ķ —Ä—É—Ö–į—Ē—ā—Ć—Ā—Ź –∑ –Ņ–Ķ–≤–Ĺ–ĺ—é —ą–≤–ł–ī–ļ—Ė—Ā—ā—é, –ľ–į—Ē —Ė–ľ–Ņ—É–Ľ—Ć—Ā —ā–į –Ķ–Ĺ–Ķ—Ä–≥—Ė—é . –Ü–ľ–Ņ—É–Ľ—Ć—Ā –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –ľ–į—Ā–ĺ—é
m
{\displaystyle m\,}
v
{\displaystyle \mathbf {v} }
p
=
m
v
{\displaystyle \mathbf {p} =m\mathbf {v} }
–ö—Ė–Ĺ–Ķ—ā–ł—á–Ĺ–į –Ķ–Ĺ–Ķ—Ä–≥—Ė—Ź —ā–į–ļ–ĺ—ó –ľ–į—ā–Ķ—Ä—Ė–į–Ľ—Ć–Ĺ–ĺ—ó —ā–ĺ—á–ļ–ł –≤ –ļ–Ľ–į—Ā–ł—á–Ĺ—Ė–Ļ –ľ–Ķ—Ö–į–Ĺ—Ė—Ü—Ė –ī–ĺ—Ä—Ė–≤–Ĺ—é—Ē
K
=
m
v
2
2
{\displaystyle K={\frac {m\mathbf {v} ^{2}}{2}}}
–ó–į–≤–ī—Ź–ļ–ł –ļ—Ė–Ĺ–Ķ—ā–ł—á–Ĺ—Ė–Ļ –Ķ–Ĺ–Ķ—Ä–≥—Ė—ó —Ą—Ė–∑–ł—á–Ĺ–Ķ —ā—Ė–Ľ–ĺ, —Ź–ļ–Ķ –ľ–į—Ē –≤—Ė–ī–ľ—Ė–Ĺ–Ĺ—É –≤—Ė–ī –Ĺ—É–Ľ—Ź —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć, –ľ–ĺ–∂–Ķ –∑–ī—Ė–Ļ—Ā–Ĺ—é–≤–į—ā–ł —Ä–ĺ–Ī–ĺ—ā—É .
–†—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź —Ä—É—Ö—É –ľ–Ķ—Ö–į–Ĺ—Ė–ļ–ł –∑–į–ī–į—é—ā—Ć –∑–≤'—Ź–∑–ĺ–ļ –ľ—Ė–∂ –Ņ—Ä–ł—Ā–ļ–ĺ—Ä–Ķ–Ĺ–Ĺ—Ź–ľ —ā—Ė–Ľ —ā–į —Ā–ł–Ľ–į–ľ–ł , —Ź–ļ—Ė –ī—Ė—é—ā—Ć –Ĺ–į —Ü—Ė —ā—Ė–Ľ–į. –ě—ā–∂–Ķ, –≤–ĺ–Ĺ–ł —Ē –ī–ł—Ą–Ķ—Ä–Ķ–Ĺ—Ü—Ė–į–Ľ—Ć–Ĺ–ł–ľ–ł —Ä—Ė–≤–Ĺ—Ź–Ĺ–Ĺ—Ź–ľ–ł —Č–ĺ–ī–ĺ —ą–≤–ł–ī–ļ–ĺ—Ā—ā–Ķ–Ļ. –Ē–Ľ—Ź –ĺ–Ņ–ł—Ā—É —á–į—Ā–ĺ–≤–ĺ—ó –Ķ–≤–ĺ–Ľ—é—Ü—Ė—ó –ľ–Ķ—Ö–į–Ĺ—Ė—á–Ĺ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –Ņ–ĺ—ā—Ä—Ė–Ī–Ĺ–ĺ –∑–į–ī–į—ā–ł –Ĺ–Ķ —ā—Ė–Ľ—Ć–ļ–ł –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—Ź —ā—Ė–Ľ, –į —Ė —ó—Ö–Ĺ—Ė —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –≤ –Ņ–ĺ—á–į—ā–ļ–ĺ–≤–ł–Ļ –ľ–ĺ–ľ–Ķ–Ĺ—ā —á–į—Ā—É. –Ě–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –≤–ł—Ā–ĺ—ā–į, –Ĺ–į —Ź–ļ—É –∑–Ľ–Ķ—ā–ł—ā—Ć –Ņ—Ė–ī–ļ–ł–Ĺ—É—ā–ł–Ļ —É–≥–ĺ—Ä—É –ľ'—Ź—á, —Ė —á–į—Ā –Ļ–ĺ–≥–ĺ –Ņ–ĺ–Ľ—Ć–ĺ—ā—É –∑–į–Ľ–Ķ–∂–į—ā—Ć –≤—Ė–ī —ā–ĺ–≥–ĺ, —Ź–ļ—É –Ņ–ĺ—á–į—ā–ļ–ĺ–≤—É —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ļ–ĺ–ľ—É –Ĺ–į–ī–į–Ľ–ł.
–Ě–Ķ–Ī–Ķ—Ā–Ĺ–į –ľ–Ķ—Ö–į–Ĺ—Ė–ļ–į –≤–ł–≤—á–į—Ē –Ņ–ĺ–≤–Ķ–ī—Ė–Ĺ–ļ—É —ā—Ė–Ľ –°–ĺ–Ĺ—Ź—á–Ĺ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł —ā–į —Ė–Ĺ—ą–ł—Ö –Ĺ–Ķ–Ī–Ķ—Ā–Ĺ–ł—Ö —ā—Ė–Ľ . –†—É—Ö —ą—ā—É—á–Ĺ–ł—Ö –ļ–ĺ—Ā–ľ—Ė—á–Ĺ–ł—Ö —ā—Ė–Ľ –≤–ł–≤—á–į—Ē—ā—Ć—Ā—Ź –į—Ā—ā—Ä–ĺ–ī–ł–Ĺ–į–ľ—Ė–ļ–ĺ—é . –í–ĺ–ī–Ĺ–ĺ—á–į—Ā —Ä–ĺ–∑–≥–Ľ—Ź–ī–į—Ē—ā—Ć—Ā—Ź –ī–Ķ–ļ—Ė–Ľ—Ć–ļ–į –≤–į—Ä—Ė–į–Ĺ—ā—Ė–≤ —Ä—É—Ö—É —ā—Ė–Ľ, —É –ļ–ĺ–∂–Ĺ–ĺ–ľ—É –∑ —Ź–ļ–ł—Ö —ā—Ė–Ľ—É —Ā–Ľ—Ė–ī –Ĺ–į–ī–į—ā–ł –Ņ–Ķ–≤–Ĺ–ĺ—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė. –Ē–Ľ—Ź –≤–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—Ź —Ā—É–Ņ—É—ā–Ĺ–ł–ļ–į –Ĺ–į –ļ–ĺ–Ľ–ĺ–≤—É –ĺ—Ä–Ī—Ė—ā—É –Ļ–ĺ–ľ—É —Ā–Ľ—Ė–ī –Ĺ–į–ī–į—ā–ł –Ņ–Ķ—Ä—ą–ĺ—ó –ļ–ĺ—Ā–ľ—Ė—á–Ĺ–ĺ—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė (–Ĺ–į–Ņ—Ä–ł–ļ–Ľ–į–ī –ī–Ľ—Ź –≤–ł–≤–Ķ–ī–Ķ–Ĺ–Ĺ—Ź –Ĺ–į –ĺ—Ä–Ī—Ė—ā—É —ą—ā—É—á–Ĺ–ĺ–≥–ĺ —Ā—É–Ņ—É—ā–Ĺ–ł–ļ–į –ó–Ķ–ľ–Ľ—Ė –≤—Ė–Ĺ –Ņ–ĺ–≤–ł–Ĺ–Ķ–Ĺ –ľ–į—ā–ł —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
1
=
{\displaystyle v_{1}=\,\!}
–≥—Ä–į–≤—Ė—ā–į—Ü—Ė–Ļ–Ĺ–Ķ –Ņ—Ä–ł—ā—Ź–≥–į–Ĺ–Ĺ—Ź –ī–ĺ–∑–≤–ĺ–Ľ–ł—ā—Ć –ī—Ä—É–≥–į –ļ–ĺ—Ā–ľ—Ė—á–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć (–Ĺ–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –ĺ–Ī'—Ē–ļ—ā—É –∑–į–Ņ—É—Č–Ķ–Ĺ–ĺ–ľ—É —Ė–∑ –ó–Ķ–ľ–Ľ—Ė –ī–Ľ—Ź –Ņ–ĺ–ī–ĺ–Ľ–į–Ĺ–Ĺ—Ź —ó—ó –≥—Ä–į–≤—Ė—ā–į—Ü—Ė—ó —Ā–Ľ—Ė–ī –Ĺ–į–ī–į—ā–ł —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć
v
2
=
{\displaystyle v_{2}=\,\!}
–Ę—Ä–Ķ—ā—Ź –ļ–ĺ—Ā–ľ—Ė—á–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ņ–ĺ—ā—Ä—Ė–Ī–Ĺ–į –ī–Ľ—Ź —ā–ĺ–≥–ĺ, —Č–ĺ–Ī –Ņ–ĺ–ļ–ł–Ĺ—É—ā–ł –∑–ĺ—Ä—Ź–Ĺ—É —Ā–ł—Ā—ā–Ķ–ľ—É , –Ņ–ĺ–ī–ĺ–Ľ–į–≤—ą–ł –Ņ—Ä–ł—ā—Ź–≥–į–Ĺ–Ĺ—Ė –∑–ĺ—Ä—Ė (–Ĺ–į–Ņ—Ä–ł–ļ–Ľ–į–ī, –ĺ–Ī'—Ē–ļ—ā, —Č–ĺ –∑–į–Ņ—É—Č–Ķ–Ĺ–ł–Ļ —Ė–∑ –ó–Ķ–ľ–Ľ—Ė –Ņ–ĺ–≤–ł–Ĺ–Ķ–Ĺ –ľ–į—ā–ł —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć 16,67 –ļ–ľ/—Ā –≤—Ė–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ó–Ķ–ľ–Ľ—Ė –Ņ—Ė–ī —á–į—Ā —Ā—ā–į—Ä—ā—É –≤ –Ĺ–į–Ļ–≤–ł–≥—Ė–ī–Ĺ—Ė—ą–ĺ–ľ—É –Ĺ–į–Ņ—Ä—Ź–ľ—Ė, –į –Ņ—Ė–ī —á–į—Ā —Ā—ā–į—Ä—ā—É —Ė–∑ –ó–Ķ–ľ–Ľ—Ė –≤ –Ĺ–į–Ļ–ľ–Ķ–Ĺ—ą –≤–ł–≥—Ė–ī–Ĺ–ĺ–ľ—É –Ĺ–į–Ņ—Ä—Ź–ľ–ļ—É –Ļ–ĺ–≥–ĺ –Ĺ–Ķ–ĺ–Ī—Ö—Ė–ī–Ĺ–ĺ —Ä–ĺ–∑—Ė–≥–Ĺ–į—ā–ł –ī–ĺ —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė 72,8 –ļ–ľ/—Ā). –ß–Ķ—ā–≤–Ķ—Ä—ā–į –ļ–ĺ—Ā–ľ—Ė—á–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –ī–ĺ–∑–≤–ĺ–Ľ–ł—ā—Ć –Ņ–ĺ–ļ–ł–Ĺ—É—ā–ł –≥–į–Ľ–į–ļ—ā–ł–ļ—É .
–®–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–≤—É–ļ—É ‚ÄĒ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ņ–ĺ—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź –Ņ—Ä—É–∂–Ĺ–ł—Ö —Ö–≤–ł–Ľ—Ć —É —Ā–Ķ—Ä–Ķ–ī–ĺ–≤–ł—Č—Ė —Ė –≤–ł–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź –Ņ—Ä—É–∂–Ĺ—Ė—Ā—ā—é —Ė –≥—É—Ā—ā–ł–Ĺ–ĺ—é —Ā–Ķ—Ä–Ķ–ī–ĺ–≤–ł—Č–į. –®–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–≤—É–ļ—É –Ĺ–Ķ —Ē —Ā—ā–į–Ľ–ĺ—é –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é —Ė –∑–į–Ľ–Ķ–∂–ł—ā—Ć –≤—Ė–ī —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ł (—É –≥–į–∑–į—Ö), –≤—Ė–ī –Ĺ–į–Ņ—Ä—Ź–ľ–ļ—É –Ņ–ĺ—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź —Ö–≤–ł–Ľ—Ė (—É –ľ–ĺ–Ĺ–ĺ–ļ—Ä–ł—Ā—ā–į–Ľ–į—Ö) –į–Ľ–Ķ –∑–į –∑–į–ī–į–Ĺ–ł—Ö –∑–ĺ–≤–Ĺ—Ė—ą–Ĺ—Ė—Ö —É–ľ–ĺ–≤ –Ņ–Ķ—Ä–Ķ–≤–į–∂–Ĺ–ĺ –Ĺ–Ķ –∑–į–Ľ–Ķ–∂–ł—ā—Ć –≤—Ė–ī —á–į—Ā—ā–ĺ—ā–ł —Ö–≤–ł–Ľ—Ė —ā–į —ó—ó –į–ľ–Ņ–Ľ—Ė—ā—É–ī–ł . –Ē–Ľ—Ź –≤–ł–Ņ–į–ī–ļ—Ė–≤, –ļ–ĺ–Ľ–ł —Ü—Ź —É–ľ–ĺ–≤–į –Ĺ–Ķ –≤–ł–ļ–ĺ–Ĺ—É—Ē—ā—Ć—Ā—Ź —Ė —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–≤—É–ļ—É –∑–į–Ľ–Ķ–∂–ł—ā—Ć –≤—Ė–ī —á–į—Ā—ā–ĺ—ā–ł, –ļ–į–∂—É—ā—Ć –Ņ—Ä–ĺ –ī–ł—Ā–Ņ–Ķ—Ä—Ā—Ė—é –∑–≤—É–ļ—É . –í–Ņ–Ķ—Ä—ą–Ķ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–≤—É–ļ—É –≤–ł–ľ—Ė—Ä—Ź–≤ –í—Ė–Ľ—Ć—Ź–ľ –Ē–Ķ—Ä—Ö–į–ľ (–į–Ĺ–≥–Ľ. William Derham ; 1657‚ÄĒ1735). –£ –≥–į–∑–į—Ö —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–≤—É–ļ—É —Ē –ľ–Ķ–Ĺ—ą–ĺ—é, –Ĺ—Ė–∂ —É —Ä—Ė–ī–ł–Ĺ–į—Ö , –į –≤ —Ä—Ė–ī–ł–Ĺ–į—Ö —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–≤—É–ļ—É –ľ–Ķ–Ĺ—ą–į –∑–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–≤—É–ļ—É —É —ā–≤–Ķ—Ä–ī–ł—Ö —ā—Ė–Ľ–į—Ö .
–í—Ė–ī–Ĺ–ĺ—ą–Ķ–Ĺ–Ĺ—Ź —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –Ņ–ĺ—ā–ĺ–ļ—É –≤ –ī–į–Ĺ—Ė–Ļ —ā–ĺ—á—Ü—Ė –≥–į–∑–ĺ–≤–ĺ–≥–ĺ —Ā–Ķ—Ä–Ķ–ī–ĺ–≤–ł—Č–į –ī–ĺ –ľ—Ė—Ā—Ü–Ķ–≤–ĺ—ó —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –Ņ–ĺ—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź –∑–≤—É–ļ—É –ľ–į—Ē –Ĺ–į–∑–≤—É ¬ę–ß–ł—Ā–Ľ–ĺ –ú–į—Ö–į¬Ľ . –®–≤–ł–ī–ļ—Ė—Ā—ā—Ć, —Č–ĺ –≤—Ė–ī–Ņ–ĺ–≤—Ė–ī–į—Ē –ú1 (1 –ú–į—Ö—É) –Ņ—Ä–ł —ā–ł—Ā–ļ—É –≤ 1 –į—ā–ľ , –ī–ĺ—Ä—Ė–≤–Ĺ—é–≤–į—ā–ł–ľ–Ķ —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –∑–≤—É–ļ—É –≤ –Ņ–ĺ–≤—Ė—ā—Ä—Ė. –†—É—Ö –ĺ–Ī'—Ē–ļ—ā—Ė–≤ –∑—Ė —ą–≤–ł–ī–ļ—Ė—Ā—ā—é, –Ņ–ĺ—Ä—Ė–≤–Ĺ—Ź–Ľ—Ć–Ĺ–ĺ—é –∑—Ė —ą–≤–ł–ī–ļ—Ė—Ā—ā—é –∑–≤—É–ļ—É, —Ā–Ņ—Ä–ł—á–ł–Ĺ—Ź—Ē –Ņ—Ä–ĺ—Ź–≤–Ľ–Ķ–Ĺ–Ĺ—Ź –Ĺ–ł–∑–ļ–ł —Ź–≤–ł—Č, —Č–ĺ —Ā—É–Ņ—Ä–ĺ–≤–ĺ–ī–∂—É—é—ā—Ć –Ņ–ĺ–ī–ĺ–Ľ–į–Ĺ–Ĺ—Ź –∑–≤—É–ļ–ĺ–≤–ĺ–≥–ĺ –Ī–į—Ä'—Ē—Ä—É . –®–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –≤—Ė–ī –ú1,2 –ī–ĺ –ú5 –Ĺ–į–∑–ł–≤–į—é—ā—Ć—Ā—Ź –Ĺ–į–ī–∑–≤—É–ļ–ĺ–≤–ł–ľ–ł , —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –Ņ–ĺ–Ĺ–į–ī –ú5 ‚ÄĒ –≥—Ė–Ņ–Ķ—Ä–∑–≤—É–ļ–ĺ–≤–ł–ľ–ł .
–ß–į—Ā –Ņ–ĺ—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź —Ā–≤—Ė—ā–Ľ–ĺ–≤–ĺ–≥–ĺ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź —É –ľ–į—Ā—ą—ā–į–Ī–ĺ–≤–į–Ĺ—Ė–Ļ –ľ–ĺ–ī–Ķ–Ľ—Ė –ó–Ķ–ľ–Ľ—Ź-–ú—Ė—Ā—Ź—Ü—Ć. –Ē–Ľ—Ź –Ņ–ĺ–ī–ĺ–Ľ–į–Ĺ–Ĺ—Ź –≤—Ė–ī—Ā—ā–į–Ĺ—Ė –≤—Ė–ī –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ—Ė –ó–Ķ–ľ–Ľ—Ė –ī–ĺ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ—Ė –ú—Ė—Ā—Ź—Ü—Ź –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—é —Ā–≤—Ė—ā–Ľ–į –Ņ–ĺ—ā—Ä—Ė–Ī–Ĺ–ĺ 1,255 —Ā –®–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ā–≤—Ė—ā–Ľ–į —É –≤–į–ļ—É—É–ľ—Ė ‚ÄĒ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė –Ņ–ĺ—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź –Ķ–Ľ–Ķ–ļ—ā—Ä–ĺ–ľ–į–≥–Ĺ—Ė—ā–Ĺ–ł—Ö —Ö–≤–ł–Ľ—Ć —É –≤–į–ļ—É—É–ľ—Ė. –Ę—Ä–į–ī–ł—Ü—Ė–Ļ–Ĺ–ĺ –Ņ–ĺ–∑–Ĺ–į—á–į—Ē—ā—Ć—Ā—Ź –Ľ—Ė—ā–Ķ—Ä–ĺ—é –Ľ–į—ā–ł–Ĺ—Ā—Ć–ļ–ĺ–≥–ĺ –į–Ľ—Ą–į–≤—Ė—ā—É ¬ęc ¬Ľ[ 8] —Ą—Ė–∑–ł—á–Ĺ–į —Ā—ā–į–Ľ–į , —Č–ĺ –Ĺ–Ķ –∑–į–Ľ–Ķ–∂–ł—ā—Ć –≤—Ė–ī –≤–ł–Ī–ĺ—Ä—É —Ė–Ĺ–Ķ—Ä—Ü—Ė–Ļ–Ĺ–ĺ—ó —Ā–ł—Ā—ā–Ķ–ľ–ł –≤—Ė–ī–Ľ—Ė–ļ—É . –í–ĺ–Ĺ–į –Ĺ–į–Ľ–Ķ–∂–ł—ā—Ć –ī–ĺ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ł—Ö —Ą—Ė–∑–ł—á–Ĺ–ł—Ö —Ā—ā–į–Ľ–ł—Ö, —Č–ĺ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—é—ā—Ć –Ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā–ĺ –ĺ–ļ—Ä–Ķ–ľ—Ė —ā—Ė–Ľ–į —á–ł –Ņ–ĺ–Ľ—Ź, –į –≤–Ľ–į—Ā—ā–ł–≤–ĺ—Ā—ā—Ė –Ņ—Ä–ĺ—Ā—ā–ĺ—Ä—É-—á–į—Ā—É –∑–į–≥–į–Ľ–ĺ–ľ. –ó–į —Ā—É—á–į—Ā–Ĺ–ł–ľ–ł —É—Ź–≤–Ľ–Ķ–Ĺ–Ĺ—Ź–ľ–ł —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ā–≤—Ė—ā–Ľ–į —É –≤–į–ļ—É—É–ľ—Ė ‚ÄĒ –≥—Ä–į–Ĺ–ł—á–Ĺ–į —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ä—É—Ö—É —Ė –Ņ–ĺ—ą–ł—Ä–Ķ–Ĺ–Ĺ—Ź –≤–∑–į—Ē–ľ–ĺ–ī—Ė–Ļ.
–Ę–ĺ—á–Ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė —Ā–≤—Ė—ā–Ľ–į –∑–į—Ą—Ė–ļ—Ā—É–≤–į–Ľ–į —Ä–Ķ–∑–ĺ–Ľ—é—Ü—Ė—Ź 117-—ó –ď–Ķ–Ĺ–Ķ—Ä–į–Ľ—Ć–Ĺ–ĺ—ó –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü—Ė—ó –ľ—Ė—Ä —Ė –≤–į–≥ [ 9]
–í —É–ļ—Ä–į—ó–Ĺ—Ā—Ć–ļ—Ė–Ļ –ľ–ĺ–≤—Ė —ā–Ķ—Ä–ľ—Ė–Ĺ —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —É–∂–ł–≤–į—Ē—ā—Ć—Ā—Ź —ā–į–ļ–ĺ–∂ –Ĺ–Ķ –≤ –ľ–Ķ—Ö–į–Ĺ—Ė—á–Ĺ–ĺ–ľ—É —Ā–Ķ–Ĺ—Ā—Ė –ī–Ľ—Ź –≤–ł–∑–Ĺ–į—á–Ķ–Ĺ–Ĺ—Ź —á–į—Ā–ĺ–≤–ł—Ö —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ –Ņ–Ķ—Ä–Ķ–Ī—Ė–≥—É –ī–ĺ–≤—Ė–Ľ—Ć–Ĺ–ł—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ė–≤ : –Ĺ–į–Ņ—Ä–ł–ļ–Ľ–į–ī, —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć —Ö—Ė–ľ—Ė—á–Ĺ–ĺ—ó —Ä–Ķ–į–ļ—Ü—Ė—ó , —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –Ĺ–į–≥—Ä—Ė–≤–į–Ĺ–Ĺ—Ź, —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –∑–į–ľ–Ķ—Ä–∑–į–Ĺ–Ĺ—Ź, —ą–≤–ł–ī–ļ—Ė—Ā—ā—Ć –≤–ł–Ņ–į—Ä–ĺ–≤—É–≤–į–Ĺ–Ĺ—Ź. –Į–ļ—Č–ĺ –Ņ–Ķ–≤–Ĺ–ł–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—Ē—ā—Ć—Ā—Ź –∑–į–Ľ–Ķ–∂–Ĺ–ĺ—é –≤—Ė–ī —á–į—Ā—É –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ—é
f
(
t
)
{\displaystyle f(t)}
d
f
(
t
)
d
t
{\displaystyle {\frac {df(t)}{dt}}}
Δ őĒ -->
t
{\displaystyle \Delta t}
f
(
t
0
+
Δ őĒ -->
t
)
− ‚ąí -->
f
(
t
0
)
Δ őĒ -->
t
{\displaystyle {\frac {f(t_{0}+\Delta t)-f(t_{0})}{\Delta t}}}
–Ą–∂–ĺ–≤ –°. –ú., –ú–į–ļ–į—Ä–Ķ—Ü—Ć –ú. –í., –†–ĺ–ľ–į–Ĺ–Ķ–Ĺ–ļ–ĺ –ě. –í. –ö–Ľ–į—Ā–ł—á–Ĺ–į –ľ–Ķ—Ö–į–Ĺ—Ė–ļ–į. ‚ÄĒ –§–Ķ–ī–ĺ—Ä—á–Ķ–Ĺ–ļ–ĺ –ź. –ú. –Ē—Ė–ī—É—Ö –õ. –Ē. ISBN 978-966-07-1817-3 .–í–į–Ļ–ī–į–Ĺ–ł—á –í. –Ü., –ü–Ķ–Ĺ—Ü–į–ļ –ď. –ú. –§—Ė–∑–ł–ļ–į. ‚ÄĒ –õ—Ć–≤—Ė–≤ : –Ě–į—Ü—Ė–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ł–Ļ –Ľ—Ė—Ā–ĺ—ā–Ķ—Ö–Ĺ—Ė—á–Ĺ–ł–Ļ —É–Ĺ—Ė–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –£–ļ—Ä–į—ó–Ĺ–ł, 2009. ‚ÄĒ 664 —Ā. ‚ÄĒ ISBN 5-7763-0227-7 .–í–ĺ–Ľ–ĺ–≤–ł–ļ –ü. –ú. –§—Ė–∑–ł–ļ–į –ī–Ľ—Ź —É–Ĺ—Ė–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā—Ė–≤. ‚ÄĒ –ö–ł—ó–≤ : –ü–Ķ—Ä—É–Ĺ, 2011. ‚ÄĒ 864 —Ā. ‚ÄĒ ISBN 966-569-172-4 .–Ü–≤–į–Ĺ–ļ—Ė–≤ –Į. –Ü., –ü–į–Ľ—é—Ö –Ď. –ú. –ú–Ķ—Ö–į–Ĺ—Ė–ļ–į [–Ę–Ķ–ļ—Ā—ā] : –Ĺ–į–≤—á. –Ņ–ĺ—Ā—Ė–Ī–Ĺ–ł–ļ –ī–Ľ—Ź —Ā—ā—É–ī. —Ą—Ė–∑. —Ā–Ņ–Ķ—Ü. –≤—É–∑—Ė–≤. ‚ÄĒ –ö–ł—ó–≤ : –Ü–°–Ē–ě, 1995. ‚ÄĒ 228 —Ā. ‚ÄĒ ISBN 5-7763-9897-5 .–ö–ĺ–∑–ł—Ü—Ć–ļ–ł–Ļ –°. –í., –ü–ĺ–Ľ—Ė—Č—É–ļ –Ē. –Ü. –ö—É—Ä—Ā –∑–į–≥–į–Ľ—Ć–Ĺ–ĺ—ó —Ą—Ė–∑–ł–ļ–ł: –Ņ—Ė–ī—Ä—É—á. –ī–Ľ—Ź —Ā—ā—É–ī. –í–Ě–ó: —É 6 —ā. –Ę. 1. –ú–Ķ—Ö–į–Ĺ—Ė–ļ–į. ‚ÄĒ –ě–ī–Ķ—Ā–į : –ź—Ā—ā—Ä–ĺ–Ņ—Ä–ł–Ĺ—ā, 2011. ‚ÄĒ 471 —Ā.–ú–Ķ—ā–ĺ–ī–ł —ā–į –∑–į—Ā–ĺ–Ī–ł –≤–ł–ľ—Ė—Ä—é–≤–į–Ĺ–Ĺ—Ź –≤–ł—Ö—Ä–ĺ–≤–ĺ–≥–ĺ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–į —ą–≤–ł–ī–ļ–ĺ—Ā—ā—Ė —ā–Ķ—á—Ė—ó: –ľ–ĺ–Ĺ–ĺ–≥—Ä–į—Ą—Ė—Ź / –í. –Ē. –ü–ĺ–≥—Ä–Ķ–Ī–Ķ–Ĺ–Ĺ–ł–ļ ; –ú-–≤–ĺ –ĺ—Ā–≤—Ė—ā–ł —Ė –Ĺ–į—É–ļ–ł –£–ļ—Ä–į—ó–Ĺ–ł, –Ě–į—Ü. —É–Ĺ-—ā ¬ę–õ—Ć–≤—Ė–≤. –Ņ–ĺ–Ľ—Ė—ā–Ķ—Ö–Ĺ—Ė–ļ–į¬Ľ. ‚ÄĒ –õ—Ć–≤—Ė–≤: –í–ł–ī-–≤–ĺ –õ—Ć–≤—Ė–≤. –Ņ–ĺ–Ľ—Ė—ā–Ķ—Ö–Ĺ—Ė–ļ–ł, 2015. ‚ÄĒ 180 —Ā. : —Ė–Ľ. ‚ÄĒ –†–Ķ–∂–ł–ľ –ī–ĺ—Ā—ā—É–Ņ—É: . ‚ÄĒ –Ď—Ė–Ī–Ľ—Ė–ĺ–≥—Ä.: —Ā. 171‚ÄĒ178 (123 –Ĺ–į–∑–≤–ł). ‚ÄĒ ISBN 978-617-607-768-8