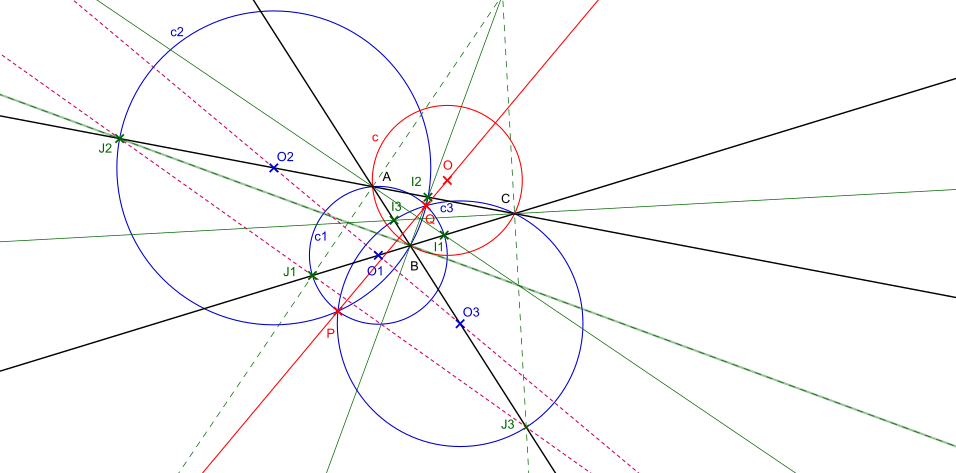
Cercles d'Apollonius
|
Read other articles:

ุงูุชุฎุจูุง ุงูุฏูุชูุฑ ุนุจุฏ ุงูุจุงุณุทู ุนููู ุงุช ุนุงู ุฉุชุงุฑูุฎ ุงูุตุฏูุฑ 1981ุงููุบุฉ ุงูุฃุตููุฉ ุงูุนุฑุจูุฉุงูุจูุฏ ู ุตุฑุงูุทุงูู ุงูู ุฎุฑุฌ ู ุญู ุฏ ุนุจุฏ ุงูุนุฒูุฒุงููุงุชุจ ูุญูุฏ ุญุงู ุฏุงูุจุทููุฉ ุนุงุฏู ุฅู ุงู ู ุฏูุญุฉ ูุงู ูุณููุฑ ุงูุจุงุจููุชุนุฏูู - ุชุนุฏูู ู ุตุฏุฑู - ุชุนุฏูู ูููู ุจูุงูุงุช ุฃูุชุฎุจูุง ุงูุฏูุชูุฑ ุณููู ุงู ุนุจุฏ ุงูุจุงุณุท ูู ูููู ููููุงู ุนุงุฏู ุฅู ุงู ...

Este artigo apresenta apenas uma fonte. Ajude a melhorar este artigo inserindo fontes adicionais.โEncontre fontes: ABW • CAPES • Google (N • L • A) (Janeiro de 2023) Esta pรกgina cita fontes, mas que nรฃo cobrem todo o conteรบdo. Ajude a inserir referรชncias. Conteรบdo nรฃo verificรกvel pode ser removido.โEncontre fontes: ABW • CAPES • Google (N • L • A) (Maio de...

Frente Nacional de la JuventudAcrรณnimo FNJTipo organizaciรณn polรญticaFundaciรณn 1977Disoluciรณn ?รrea de operaciรณn Espaรฑa[editar datos en Wikidata] El Frente Nacional de la Juventud (FNJ) fue una organizaciรณn polรญtica espaรฑola neofascista constituida en Barcelona en septiembre de 1977.[1][2] Se tratรณ de una escisiรณn de Fuerza Joven (juventudes de Fuerza Nueva), dirigida por Ramรณn Graells Bofill y que consiguiรณ extender la militancia a Navarra, Aragรณn y Ast...

Coordenadas: 37ยฐ 42' 54 N 8ยฐ 39' 53 O Portugal Sรฃo Martinho das Amoreiras Freguesia Sรญmbolos Brasรฃo de armas Localizaรงรฃo Sรฃo Martinho das AmoreirasLocalizaรงรฃo de Sรฃo Martinho das Amoreiras em Portugal Coordenadas 37ยฐ 42' 54 N 8ยฐ 39' 53 O Regiรฃo Alentejo Sub-regiรฃo Alentejo Litoral Distrito Beja Municรญpio Odemira Cรณdigo 021107 Administraรงรฃo Tipo Junta de freguesia Caracterรญsticas geogrรกficas รrea total 14...

Zรผrich im Siegfriedatlas Der Topographische Atlas der Schweiz, inoffiziell auch Siegfriedatlas oder Siegfriedkarte genannt, ist ein amtliches Kartenwerk der Schweiz, dessen Herausgabe durch das Eidgenรถssische Topographische Bureau unter Hermann Siegfried begonnen wurde und von 1870 bis 1926[1] dauerte. Insbesondere die Hochgebirgsblรคtter mit 117 monochromen Stichen von Rudolf Leuzinger fanden im In- und Ausland Beachtung. Da es sich nach heutigem Sprachgebrauch nicht um einen Atlas...

Melvin Stewart Medallista olรญmpico Datos personalesNacimiento Gastonia (Estados Unidos)16 de noviembre de 1968Nacionalidad(es) EstadounidenseCarrera deportivaDeporte Nataciรณn Medallero Nataciรณn Estados Unidos Juegos Olรญmpicos OroBarcelona 1992200 m mariposa OroBarcelona 19924x100 m estilos] BronceBarcelona 19924x200 m libre [editar datos en Wikidata] Melvin Stewart (Estados Unidos, 16 de no...

ูุฐู ุงูู ูุงูุฉ ูุชูู ุฉ ุฅุฐ ุชุตู ุฅูููุง ู ูุงูุงุช ุฃุฎุฑู ููููุฉ ุฌุฏูุง. ูุถููุงุ ุณุงุนุฏ ุจุฅุถุงูุฉ ูุตูุฉ ุฅูููุง ูู ู ูุงูุงุช ู ุชุนููุฉ ุจูุง. (ููููู 2019) ุฎูุณูุณ ุฅุฏูุงุฑุฏู ุฃู ุงุฑุงู ู ุนููู ุงุช ุดุฎุตูุฉ ุงูู ููุงุฏ ุณูุฉ 1927 (ุงูุนู ุฑ 95–96 ุณูุฉ) ู ูุงุทูุฉ ุงูููุงูุงุช ุงูู ุชุญุฏุฉ ุงูุญูุงุฉ ุงูุนู ููุฉ ุงูู ุฏุฑุณุฉ ุงูุฃู ูููุฉ ุงูููุฏุณุฉ ูู ุฌุงู ุนุฉ ููุฑูููู...

ๆญคๆข็ฎๆฒกๆๅๅบไปปไฝๅ่ๆๆฅๆบใ (2009ๅนด3ๆ8ๆฅ)็ถญๅบ็พ็งๆๆ็ๅ งๅฎน้ฝๆ่ฉฒๅฏไพๆฅ่ญใ่ฏทๅๅฉ่ฃๅ ๅฏ้ ๆฅๆบไปฅๆนๅ่ฟ็ฏๆก็ฎใๆ ๆณๆฅ่ฏ็ๅ งๅฎนๅฏ่ฝๆๅ ็บ็ฐ่ญฐๆๅบ่่ขซ็งป้คใ ๆญฃๅธธ็ๅบ็ฃๅพ็ๆดปๅๅThe Normal Christian Lifeไฝ่ ๅชๆๅฃฐ็ฑปๅไธญๅฝๅบ็ฃๆๆฐๆๅฐๆนๆไผ่ฏญ่จ่ฑ่ฏญใๆฑ่ฏญ็ญๅค็ง่ฏญ่จไธป้ขๅบ็ฃๅพ็ๆดป็ผ่กไฟกๆฏๅบ็ๆบๆไธๆตท็ฆ้ณไนฆๆฟๅฐๆนพ็ฆ้ณไนฆๆฟใๆฐดๆต่ไบ็ซๅบ็ๅฐ ไธญ่ฏๆฐ...

ใใฎ่จไบใฏๆค่จผๅฏ่ฝใชๅ่ๆ็ฎใๅบๅ ธใๅ จใ็คบใใใฆใใชใใใไธๅๅใงใใๅบๅ ธใ่ฟฝๅ ใใฆ่จไบใฎไฟก้ ผๆงๅไธใซใๅๅใใ ใใใ๏ผใใฎใใณใใฌใผใใฎไฝฟใๆน๏ผๅบๅ ธๆค็ดข?: ไธญ้่ญฆๅฏ็ฝฒ ๆฑไบฌ้ฝ โ ใใฅใผใน ยท ๆธ็ฑ ยท ในใซใฉใผ ยท CiNii ยท J-STAGE ยท NDL ยท dlib.jp ยท ใธใฃใใณใตใผใ ยท TWL๏ผ2014ๅนด9ๆ๏ผ ่ญฆ่ฆๅบไธญ้่ญฆๅฏ็ฝฒ ้ฝ้ๅบ็่ญฆๅฏ ่ญฆ...

This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Stephen Portman โ news ยท newspapers ยท books ยท scholar ยท JSTOR (January 2018) (Learn how and when to remove this template message) Stephen Portman ...

Part of a series on the History of California Periods Before 1900 Province of Las Californias Alta California California Republic Conquest of California Interim governments California Gold Rush Since 1900 Topics Maritime Wine Newspapers Bread Railroads Highways Slavery Eugenics Oil Cities Anaheim Chico Fresno Los Angeles Oakland Pasadena Piedmont Riverside Sacramento San Bernardino San Diego San Francisco San Jose Santa Barbara Santa Monica Visalia Regions Bay Area San Fernando Valley Santa C...

Italian neo-Nazi and neo-Fascist intellectual Franco FredaFreda talks to his lawyers during a trialBorn (1941-02-11) 11 February 1941 (age 82)Padua, ItalyNationalityItalianOrganizationOrdine NuovoKnown forNazi-Maoism, Piazza Fontana bombing (disputed) Franco Giorgio Freda (born 11 February 1941) is one of the leading neo-Nazi and neo-Fascist intellectuals of the post-war Italian far-right. He founded a publishing house for neo-Nazi thought, and described himself as an admirer of Hit...

1983 single by Bryan AdamsCuts Like a KnifeSleeve for Canadian singleSingle by Bryan Adamsfrom the album Cuts Like a Knife B-sideLonely NightsReleasedMay 27, 1983GenreRockLength5:16 (Album Version)4:05 (Single Version)LabelA&MSongwriter(s)Bryan Adams, Jim VallanceProducer(s)Bryan Adams, Bob ClearmountainBryan Adams singles chronology Straight from the Heart (1983) Cuts Like a Knife (1983) This Time (1983) Cuts Like a Knife is a song by Canadian rock musician Bryan Adams. It was released i...

Walaupun ukuran fisiknya yang kecil, bukanlah alasan bagi Singapura untuk tidak bisa membagi wilayah negaranya menjadi subdivisi nasional dalam bentuk provinsi dan wilayah politik nasional lainnya yang biasa ditemukan di beberapa negara besar lainnya, meskipun dalam sepanjang sejarah sebuah negara kota dibagi dengan tujuan untuk mengatur pemerintahan di tingkat daerah dan perencanaan tata kota. Berdasarkan sejarahnya, pembagian subdivisi ini berdasarkan pada wilayah per kabupaten, terutama pa...

4400 ๆช็ฅใใใฎ็้่ ใธใฃใณใซ ๆตทๅคใใฉใใSFใ็คพไผๆดพใในใใชใผๅบๆผ่ ็ปๅ ดไบบ็ฉใๅ็ ง ๆพ้ๆพ้ๅฝใปๅฐๅ ใขใกใชใซๅ่กๅฝ ใทใผใบใณ1ๆพ้ๆ้2004ๅนด7ๆ11ๆฅ - 8ๆ8ๆฅๅๆฐ6ใใฉใใฆใณใใปใธใฃใใณ ใทใผใบใณ2ๆพ้ๆ้2005ๅนด6ๆ5ๆฅ - 8ๆ28ๆฅๅๆฐ13ใใฉใใฆใณใใปใธใฃใใณ ใทใผใบใณ3ๆพ้ๆ้2006ๅนด6ๆ11ๆฅ - 8ๆ27ๆฅๅๆฐ13ใใฉใใฆใณใใปใธใฃใใณ ใทใผใบใณ4ๆพ้ๆ้2007ๅนด6ๆ17ๆฅ - 9ๆ...

ุฌุณุฑ ุฑูุณูู ุงูุฌุณุฑ ุฃู ุงูููุทุฑุฉ (ุฌ ุงูููุงุทุฑ) ูู ู ููุดุฃ ููุณุชุฎุฏู ููุนุจูุฑ ู ู ู ูุงู ุฅูู ุขุฎุฑ ุจูููู ุง ุนุงุฆู.[1][2] ูุงุฆู ุฉ ุงูุฌุณูุฑ ุฑูุณูุง ุชุญุชูู ูุฐู ุงููุงุฆู ุฉ ุนูู ุฃุณู ุงุก ุงูุฌุณูุฑ ูู ุฑูุณูุง. ุงูุฌุณุฑ ุงูู ุตุฑู ุฌุณุฑ ุฃูุณุงู ุฌุณุฑ ุจููุดูุชุดููุณูู ุฌุณุฑ ุชูู ูุฑููุชุณูู ุฌุณุฑ ุฑูุณูู ุฌุณุฑ ููุฑูุดููููุณูู ุฌุณุฑ ููููุดููู ู ุฑุงุฌุน ^ Iron...

Pasaporte del Mandato de Palestina La portada de un pasaporte del Mandato de Palestina.Tipo PasaporteEmisor Mandato Britรกnico de Palestina[editar datos en Wikidata] Antes de los pasaportes oficiales emitidos por el Mandato, los britรกnicos emitieron un documento de viaje, como se ve en este ejemplo desde 1924. La entidad emisora se da como Palestine en inglรฉs, ููุณุทูู (Palestina) en รกrabe y (ืคืืฉืชืื ื (ืืดื (Palestina mรกs el acrรณnimo de Eretz Yisrael (Tierra de Isra...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (November 2021) Chinna Gollapalem Island is a river delta island formed by the Upputeru Rivulet in Andhra Pradesh, India. The island is located in the Kruthivennu mandal of Krishna District. The island faces constant threats from soil erosion due to flooding from the Upputeru River, which is the only outlet of the Kolleru Lake.[1 ...

British actor Julian L'EstrangeBornJulian Boyle6 August 1880Weston-super-Mare, EnglandDied22 October 1918 (aged 38)New York City, New York, U.S.OccupationActorYears active1902โ18Spouse Constance Collier (m. 1905) Julian L'Estrange (born Julian Boyle; 6 August 1880 โ 22 October 1918) was an English-born stage actor who later made a handful of silent films for Paramount Pictures. He married fellow performer Constance Collier at All Saints Church in London...

C-class light cruiser of the British Royal Navy For other ships with the same name, see HMS Coventry. History United Kingdom NameHMS Coventry BuilderSwan Hunter and Wigham Richardson, Wallsend-on-Tyne Laid down4 August 1916 Launched6 July 1917 Commissioned21 February 1918 ReclassifiedConverted to anti-aircraft cruiser before the Second World War FateDamaged and scuttled 14 September 1942 Badge General characteristics Displacement4,190 tons Length450 ft (140 m) Beam43.6 ft (13.3...