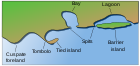
Wave shoaling
|
Read other articles:

Ірина МальгінаІрина Анатоліївна Мальгіна Загальна інформаціяНаціональність росіянкаГромадянство РосіяМісце проживання Ханти-МансійськНародження 8 червня 1973(1973-06-08) (50 років)МурманськЗріст 169 смВага 60 кгСпортКраїна РосіяВид спорту біатлонЗавершення виступів 2007 Уча

تسنيم في تفسیر القرآن غلاف الكتاب الاسم تسنيم في تفسیر القرآن المؤلف عبد الله الجوادي الآملي الموضوع تفسیر شیعي للقرآن العقيدة إسلام البلد إيران اللغة الفارسية معلومات الطباعة كتب أخرى للمؤلف الحياة العرفانية للإمام علي، الحماسة والعرفان و... تعديل مصدري - تعديل تسنيم...

Archaeognatha Petrobius maritimus (en) TaksonomiKerajaanAnimaliaFilumArthropodaKelasInsectaOrdoArchaeognatha Börner, 1904 lbs Archaeognatha adalah ordo primitif dari serangga. Nama Archeognatha berasal dari bahasa Yunani, archaios yang berarti primitif dan gnathos yang berarti rahang. Ordo serangga ini rata-rata panjangnya 10-12mm merupakan ordo serangga tak bersayap. Serangga berbentuk silindris ini juga tidak bermetamorfosis, hanya berganti kulit sebanyak 20-70 kali. Serangga nokturnal ini...

1929 song by Jerome Kern and Oscar Hammerstein II Why Was I Born?Single by Helen MorganB-sideDon't Ever Leave MeWritten1929Published1929 T.B. Harms, Inc., Universal Polygram International Publishing, Inc.[1]ReleasedJanuary 20, 1930[2]RecordedOctober 16, 1929 take 2[3]StudioNew York CityVenueSweet Adeline (1929 Broadway musical)GenreShow tune, Popular MusicLength3.22LabelVictor 22199Composer(s)Jerome KernLyricist(s)Oscar Hammerstein II Why Was I Born? is a 1929 song com...

DoraDoraDoraDora album cover.Album mini karya U-KISSDirilis25 April 2012 (2012-04-25) (see release history)Direkam2011-2012GenrePop, electropopLabelNH Media, KT Music, LOEN Entertainment, Sony Music (South Korea)Kronologi U-KISS Bran New Kiss(2011)Bran New Kiss2011 DoraDora(2012) The Special to Kissme(2012)The Special to Kissme2012 Singel dalam album DoraDora DoraDoraDirilis: 25 April 2012 (2012-04-25) DoraDora adalah album mini oleh boyband Korea Selatan, U-KISS. Ini adalah EP ...

Character from The Wire Fictional character Roland PryzbylewskiThe Wire characterJim True-Frost as Roland PryzbylewskiFirst appearanceThe Detail (2002)Last appearance–30– (2008)Created byDavid SimonPortrayed byJim True-FrostIn-universe informationAliasPrez Mr. PrezboGenderMaleOccupationDetective School teacherSpouseJudy PryzbylewskiRelativesStanislaus Valchek (father-in-law) Roland Prez Pryzbylewski is a fictional character on the HBO drama The Wire, played by actor Jim True-Frost. Pryzby...

For the federal constituency formerly represented in the Dewan Rakyat, see Renggam (federal constituency). Mukim in Johor, MalaysiaRenggamMukimCountryMalaysiaStateJohorDistrictKluangArea • Total557 km2 (215 sq mi)Population • Total47,510 • Density85/km2 (220/sq mi) Renggam (also spelled Rengam) is a town and mukim in Kluang District, Johor, Malaysia. Geography Rengam in Kluang District The mukim spans over an area of 557 km2.[1&...

Liturgical chant used by the Ethiopian Orthodox Tewahedo Church Zema redirects here. For the name, see Zema (name). Ethiopian liturgical chantSaint Yared and his disciples singingNative nameZemaStylistic originsAncient liturgical chantCultural originsEthiopian Orthodox Tewahedo ChurchTypical instrumentsKeberodrumstsanatselsistrummequamia Part of a series onOriental Orthodoxy Oriental Orthodox churches Coptic Syriac Armenian Indian Cilicia Orthodox Tewahedo Ethiopian Eritrean Independent churc...

Governor of Saint HelenaCoat of arms of Saint HelenaStandard of the Governor of Saint HelenaIncumbentNigel Phillipssince 13 August 2022StyleHis ExcellencyResidencePlantation House, St HelenaAppointerMonarch of the United KingdomTerm lengthAt His Majesty's pleasureFormation1659First holderJohn DuttonWebsiteGovernment of St Helena Politics of Saint Helena The CrownThe Monarch Charles III Heir Apparent William, Prince of Wales GovernmentGovernor Nigel Phillips Executive Council Chief Minist...

Arab Muslim theologian, writer and scholar (767–820) Imam Shafi redirects here. For the village in Iran, see Emam Safi. For the Egyptian surname with the same Arabic spelling, see El-Shafei. al-Shafi'iاَلشَّافِعِيُّTitleShaykh al-IslāmPersonalBorn767 CE 150 AH Gaza[citation needed], Abbasid CaliphateDied19 January 820 CE (aged 54) 204 AH al-Fustat, Abbasid CaliphateReligionIslamEraIslamic Golden AgeDenominationSunniJurisprudenceMujtahidMain interest(s)Fiqh, HadithNota...

Sporting event delegationSan Marino at the2020 Summer OlympicsIOC codeSMRNOCComitato Olimpico Nazionale SammarineseWebsitewww.cons.sm (in Italian)in Tokyo, JapanJuly 23, 2021 (2021-07-23) – August 8, 2021 (2021-08-08)Competitors5 in 4 sportsFlag bearers (opening)Arianna ValloniMyles AmineFlag bearer (closing)Myles AmineMedalsRanked 72nd Gold 0 Silver 1 Bronze 2 Total 3 Summer Olympics appearances (overview)1960196419681972197619801984198819921996...

Suburb of Portsmouth, England This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (September 2022) (Learn how and when to remove this template message) Human settlement in EnglandDraytonDrayton is astri...

Chinese rock musician and composer (born 1971) In this Chinese name, the family name is Wang (汪). You can help expand this article with text translated from the corresponding article in Chinese. (June 2020) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machin...

1969 studio album by The HolliesHollies Sing DylanStudio album by The HolliesReleasedMay 1969RecordedAugust 1968[1][2]StudioAbbey Road Studios, LondonGenreRock, popLength36:07LabelUK: ParlophoneProducerRon RichardsThe Hollies chronology Hollies' Greatest(1968) Hollies Sing Dylan(1969) Hollies Sing Hollies(1969) The Hollies US chronology Dear Eloise / King Midas in Reverse(1967) Words and Music by Bob Dylan(1969) He Ain't Heavy, He's My Brother(1969) Professional rating...

Medication OmaveloxoloneClinical dataTrade namesSkyclarysOther namesRTA 408License data US DailyMed: Omaveloxolone Routes ofadministrationBy mouthATC codeNoneLegal statusLegal status US: ℞-only[1] Identifiers IUPAC name N-((4aS,6aR,6bS,8aR,12aS,14aR,14bS)-1 1-cyano-2,2,6a,6b,9,9,12a-heptamethyl-10,14-dioxo-1,2,3,4,4a,5,6,6a,6b,7,8,8a,9,10,12a,14,14a,14b- octadecahydropicen-4a-yl)-2,2-difluoropropanamide CAS Number1474034-05-3 YPubChem CID71811910IUPHAR/BPS7573Dru...

У этого термина существуют и другие значения, см. Дети кукурузы. Дети кукурузыChildren of the Corn Жанр ужасы Автор Стивен Кинг Язык оригинала Английский Дата написания 1977 Дата первой публикации 1977 «Дети кукурузы» (англ. Children of the Corn) — рассказ американского писателя Стивена ...

Unincorporated community in Michigan, United StatesDeer Park, MichiganUnincorporated communityLooking north along County Road 407Deer ParkLocation within the state of MichiganShow map of MichiganDeer ParkLocation within the United StatesShow map of the United StatesCoordinates: 46°40′28″N 85°36′59″W / 46.67444°N 85.61639°W / 46.67444; -85.61639CountryUnited StatesStateMichiganCountyLuceTownshipMcMillanEstablished1876Elevation640 ft (200 m)Time zon...
Internet application suite Beonex CommunicatorBeonex Communicator 0.6 displaying the Book of MozillaOriginal author(s)Ben BuckschDeveloper(s)Beonex Business ServicesInitial releaseNeverPreview release0.8.2-stable / 21 March 2003 Written inC++, XUL, XBL, JavaScriptOperating systemMicrosoft Windows, Mac OS X, Linux, FreeBSDAvailable inEnglish, GermanTypeInternet suiteLicenseMPL/Netscape Public License[1]Websitewww.beonex.com Beonex Communicator is a discontinued open-source Internet sui...

Wakil Wali Kota ProbolinggoLambang Kota Probolinggo Republik IndonesiaPetahanamasih lowongsejak 9 Desember 2020Masa jabatan5 tahunDibentuk2004Pejabat pertamaBandyk SutrisnoSitus webprobolinggokota.go.id Wakil Wali Kota Probolinggo adalah posisi kedua yang memerintah Kota Probolinggo di bawah Wali Kota Probolinggo. Posisi ini pertama kali dibentuk pada tahun 2004. Daftar No Wakil Wali Kota Mulai Jabatan Akhir Jabatan Prd. Ket. Wali Kota 1 Bandyk Sutrisno 2004 2009 1 H.M. BuchoriS.H...

Go-kart race at Purdue University This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Purdue Grand Prix – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this template message) Purdue Grand PrixVenueGrand Prix Track, Northwest Sports Complex, Purdue UniversityLocationWest Laf...

























![{\displaystyle H\,{\sqrt[{4}]{h}}={\text{constant}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7a7c8f81ffbc4b7b6c26ee815f763e09871f723)
![{\displaystyle {\sqrt[{4}]{h}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e6decf5b49fd506f06f0b5250e58db38a41efda)