Semigruppo
|
Read other articles:

Лесь Курбасукр. Лесь Курбас Имя при рождении укр. Олександр-Зенон Степанович Курбас Дата рождения 25 февраля 1887(1887-02-25)[1][2] Место рождения Самбор, Австро-Венгрия Дата смерти 3 ноября 1937(1937-11-03)[2] (50 лет) Место смерти Сандармох, Повенецкий сельский совет, Медвежьег�...

German general (1886–1944) Carl-Heinrich von StülpnagelBorn(1886-01-02)2 January 1886Berlin, German EmpireDied30 August 1944(1944-08-30) (aged 58)Plötzensee Prison, Berlin, Nazi Germany Cause of deathExecution by hanging Allegiance German Empire Weimar Republic Nazi GermanyService/branch Imperial German Army Reichsheer German ArmyYears of service1904–44Rank GeneralCommands held17th ArmyBattles/warsWorld War I World War IIAwardsKnight's Cross...

Ектоін Систематична назва 1,4,5,6-тетрагідро-(S)-2-метил-4-пірімідинкарбонова кислота Ідентифікатори Номер CAS 96702-03-3KEGG C06231ChEBI 27592SMILES CC1=NCCC(N1)C(=O)O[1]InChI InChI=1S/C6H10N2O2/c1-4-7-3-2-5(8-4)6(9)10/h5H,2-3H2,1H3,(H,7,8)(H,9,10)/t5-/m0/s1Номер Бельштейна 7288977 Властивості Молекулярна формула C6H10N2O2 Молярна маса 142,2 г/мол

Leão Branco Leão-sul-africano leucístico Estado de conservação Vulnerável Classificação científica Reino: Animalia Filo: Chordata Classe: Mammalia Ordem: Carnivora Família: Felidae Género: Panthera Espécie: P. leo Subespécie: P. leo krugery Nome trinomial Panthera leo krugeriRoberts, 1929 O Leão-branco é uma rara mutação de cor do leão-sul-africano (Panthera leo krugeri), devido a uma particularidade genética chamada leucismo. O leão branco não constitui uma subespécie s...

Der Titel dieses Artikels ist mehrdeutig. Zum Pfarrer und kurfürstlichen Rat von Friedrich I. von Brandenburg-Ansbach siehe Friedrich Sesselmann (Pfarrer). Friedrich Sesselmann (* um 1410 in Kulmbach, Oberfranken; † 21. September 1483 in Kamenz, Oberlausitz) war Kanzler in Brandenburg seit 1445, Bischof von Lebus seit 1455 und Regent des Kurfürstentums Brandenburg seit 1473. Inhaltsverzeichnis 1 Leben 1.1 Herkunft und Studien 1.2 Kanzler in Brandenburg 1.3 Bischof von Lebus 1.4 Statthalte...
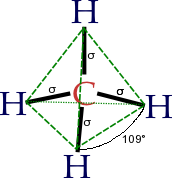
Struktur dari molekul metana: ikatan hidrokarbon yang paling sederhana. Kimia organik adalah percabangan studi ilmiah dari ilmu kimia mengenai struktur, sifat, komposisi, reaksi, dan sintesis senyawa organik. Senyawa organik dibangun terutama oleh karbon dan hidrogen, dan dapat mengandung unsur-unsur lain seperti nitrogen, oksigen, fosfor, halogen dan belerang. Definisi asli dari kimia organik ini berasal dari kesalahpahaman bahwa semua senyawa organik pasti berasal dari organisme hidup, teta...

Wollemia Ocorrência: Cretáceo Médio; recente Espécime jovem num jardim botânico. Classificação científica Reino: Plantae Divisão: Pinophyta Classe: Pinopsida Ordem: Araucariales Família: Araucariaceae Género: Wollemia Espécie: W. nobilis Nome binomial Wollemia nobilisW.G.Jones, K.D.Hill & J.M.Allen Wollemia é um género de árvore conífera da família Araucariaceae. A espécie australiana Wollemia nobilis é a única espécie deste género e foi descoberta em 1994 num conjun...

DjoenarsaAnggota Badan Pemeriksa KeuanganMasa jabatan10 Agustus 1983 – 13 Agustus 1988Anggota Dewan Perwakilan RakyatMasa jabatan13 Februari 1968 – 1 Oktober 1977PresidenSoeharto Informasi pribadiLahir(1922-01-25)25 Januari 1922Semarang, Hindia BelandaMeninggal2 Agustus 1996(1996-08-02) (umur 74)Karier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik IndonesiaMasa dinas1952—1978Pangkat Mayor Jenderal PolisiSatuanReserseSunting kotak info

Isla Gladstone Conservatory Stanley ParkTypeMunicipalLocationLiverpoolArea45 hectaresCreated14 May 1870StatusOpen all year A map of Stanley Park from 1947 Stanley Park is a 110 acres (45 ha) park in Liverpool, England, designed by Edward Kemp, which was opened on 14 May 1870 by the Mayor of Liverpool, Joseph Hubback. It is significant among Liverpool's parks on account of its layout and architecture. It has a grand terrace with expansive bedding schemes that were once highlighted by foun...

Political party in Austria Fatherland Front Vaterländische FrontFederal leaderEngelbert Dollfuß(20 May 1933 – 25 July 1934)Ernst Starhemberg(31 July 1934 – 15 May 1936)[1]Founded20 May 1933; 90 years ago (1933-05-20)Dissolved13 March 1938; 85 years ago (1938-03-13)Merger ofCS, Landbund, HeimwehrYouth wingÖsterreichisches Jungvolk[2]Paramilitary wingAssault Corps [de][3]Membership3,000,000 (1937 est.)[...

Este artículo o sección tiene referencias, pero necesita más para complementar su verificabilidad.Este aviso fue puesto el 2 de marzo de 2021. Una especie generalista es aquella especie capaz de desarrollarse en una amplia gama de condiciones ambientales y que puede hacer uso de una amplia variedad de recursos. Por ejemplo, un animal omnívoro tiene un dieta alimentaria muy amplio, es un animal oportunista que adapta de inmediato su dieta a los recursos disponibles. Así pues, una especie ...

Fan community of American singer Jackson in 1992 Fans of American singer Michael Jackson are known as Moonwalkers.[1] History This section needs to be updated. Please help update this article to reflect recent events or newly available information. (August 2021) Origins Jacksonmania In the beginning of the 1970s, Jackson and his brothers would embark on tours across the globe, performing in front of millions of fans while recording hits at a rapid pace during the Jackson-mania. Adulat...

Communauté de communesDombes Saône Vallée Region(en) Auvergne-Rhône-Alpes Département(s) Ain Gründungsdatum 1. Januar 2014 Rechtsform Communauté de communes Verwaltungssitz Trévoux Gemeinden 19 Präsident Bernard Grison SIREN-Nummer 200 042 497 Fläche 179,48 km² Einwohner 39.725 (2020)[1] Bevölkerungsdichte 221 Einw./km² Website www.ccdsv.fr Lage des Gemeindeverbandesin der Region Auvergne-Rhône-Alpes Die Communauté de communes Dombes Saône ...

Sporting event delegationPoland at the1968 Winter OlympicsIOC codePOLNOCPolish Olympic CommitteeWebsitewww.pkol.pl (in Polish)in GrenobleCompetitors31 (23 men, 8 women) in 7 sportsFlag bearersStanisław Szczepaniak, BiathlonMedals Gold 0 Silver 0 Bronze 0 Total 0 Winter Olympics appearances (overview)192419281932193619481952195619601964196819721976198019841988199219941998200220062010201420182022 Poland competed at the 1968 Winter Olympics in Grenoble, France. Alpine skiing Main arti...

Flag of the city of Baltimore, Maryland, US Baltimore, MarylandProportion2:3AdoptedFebruary 11, 1915DesignPaly of six Or and sable, a bend counterchanged, on an inescutcheon Sable, within an orle of the first, a representation of Baltimore's Battle Monument (from the War of 1812, constructed 1815-1822), Argent.Designed byJudge Henry StockbridgeCarroll LucasWilbur F. CoyleHester Dorsey Richardson Flag of Baltimore 1899–1915 The flag of the city of Baltimore features the Battle Monument,...

1949 British coming-of-age romance and adventure film directed by Frank Launder For other uses, see Blue Lagoon. The Blue LagoonLobby cardDirected byFrank LaunderWritten byNovel: Henry De Vere Stacpoole Screenplay: John Baines Michael Hogan Frank LaunderProduced bySidney Gilliat Frank LaunderStarring Jean Simmons Donald Houston Noel Purcell James Hayter Cyril Cusack CinematographyGeoffrey UnsworthEdited byThelma ConnellMusic byClifton ParkerDistributed byGeneral Film DistributorsRelease date1...

ديفيد سيماو معلومات شخصية الميلاد 15 مايو 1990 (33 سنة)[1] فرساي الطول 1.83 م (6 قدم 0 بوصة) مركز اللعب وسط الجنسية البرتغال معلومات النادي النادي الحالي أروكا الرقم 5 مسيرة الشباب سنوات فريق 1998–2000 Abóboda 2000–2009 بنفيكا المسيرة الاحترافية1 سنوات فريق م. (هـ.) 2008–2013 �...

Artikel biografi ini ditulis menyerupai resume atau daftar riwayat hidup (Curriculum Vitae). Tolong bantu perbaiki agar netral dan ensiklopedis. Ini adalah nama Mandailing, marganya adalah Nasution. Darmin NasutionDarmin pada 2016Menteri Koordinator Bidang Perekonomian Indonesia ke-16Masa jabatan12 Agustus 2015 – 20 Oktober 2019PresidenJoko WidodoPendahuluSofyan DjalilPenggantiAirlangga HartartoMenteri Koordinator Bidang Pembangunan Manusia dan Kebudayaan IndonesiaPelaksana Tug...

Valley in Kunar Province, Afghanistan This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Korangal Valley – news · newspapers · books · scholar · JSTOR (August 2021) (Learn how and when to remove this template message) 34°53′N 70°55′E / 34.89°N 70.91°E / 34.89; 70.91 Korangal Vall...

Spanish Catholic bishop (born 1965) In this Spanish name, the first or paternal surname is Cobo and the second or maternal family name is Cano. His EminenceJosé Cobo CanoCardinal, Metropolitan Archbishop of MadridCobo in 2014ChurchRoman Catholic ChurchArchdioceseMadridSeeMadridAppointed12 June 2023Installed8 July 2023PredecessorCarlos Osoro SierraOther post(s)Cardinal-Priest of Santa Maria in Monserrato degli Spagnoli (2023–)OrdersOrdination23 April 1994by Angel Suquía Goicoe...


























