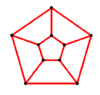
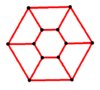
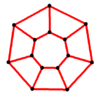
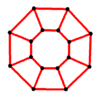
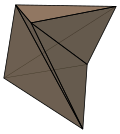
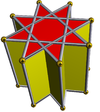
Prism (geometry)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Untuk kegunaan lain, lihat SOS (disambiguasi). SOS SOS adalah nama untuk tanda bahaya kode Morse internasional. (• • • - - - • • •). Tanda ini pertama kali digunakan oleh pemerintah Jerman pada 1 April 1905, dan menjadi standar di seluruh dunia sejak 3 November 1906. Dalam kode Morse, tiga titik adalah kode untuk huruf S dan tiga garis adalah huruf O. Dalam penggunaannya, SOS sering dihubungkan dengan singkatan kata Save Our Ship, Save Our S...

У этого термина существуют и другие значения, см. How Great Thou Art. Карл Густав Боберг «Великий Бог» — известный в мире под английским названием «How Great Thou Art» (Как Ты велик!) христианский гимн XIX века. Текст гимна основан на стихотворении шведского поэта Карла Густава Боберга (1...

Article principal : Renault Espace. Renault Espace Un Renault Espace I phase 1. Marque Renault Années de production 1984 - 1991Phase 1 : 1984 - 1988Phase 2 : 1988 - 1991 Production 191 694 exemplaire(s) Classe Monospace Usine(s) d’assemblage Romorantin-Lanthenay Moteur et transmission Énergie Essence, diesel Moteur(s) Essencemoteur Douvrin:1 995 cm32 165 cm3Diesel turbomoteur Douvrin:2 068 cm3 Position du moteur Longitudinale avant Cy...

David F. Hendry in 1992 David Forbes Hendry FBA (Nottingham, 6 maart 1944) is een Brits econometrist. Hij werd in 1982 hoogleraar economie aan de Universiteit van Oxford. Van 2001 tot en met 2007 was hij ook hoofd van de economische faculteit van de Universiteit van Oxford. Hij is ook fellow aan Nuffield College, een van de deelcolleges van de Universiteit van Oxford. In 1970 ontving hij zijn PhD van de London School of Economics (LSE). Zijn promotor was John Denis Sargan. Tot zijn overstap, ...

Демофонт звільняє Етру Етра, також Ефра (грец. Αίθρα) — дочка Піттея, царя Тройзену, дружина Егея, мати Тесея. За одним із переказів, Етру викрали Діоскури, і вона стала рабинею Єлени, з якою прибула до Трої. Етра — дочка Океана, дружина Атланта, від якого в неї народили�...

Local municipality in Western Cape, South AfricaBitou PlettLocal municipality SealLocation of Bitou Local Municipality within the Western CapeCoordinates: 33°55′S 23°25′E / 33.917°S 23.417°E / -33.917; 23.417CountrySouth AfricaProvinceWestern CapeDistrictGarden RouteSeatPlettenberg BayWards7Government[1] • TypeMunicipal council • MayorDave Swart (DA)Area • Total992 km2 (383 sq mi)Population (2011)&...

Đường chân trời thành phố Hải Phòng vào tháng 7/2023 nhìn từ sông Cấm. Hải Phòng là thành phố TTTƯ lớn thứ 3 Việt Nam và là thành phố cảng lớn nhất đất nước. Thành phố hiện có 46 tòa nhà đã hoàn thành (bao gồm 16 tòa nhà trọc trời trên 100 mét và 32 tòa nhà cao tầng). Tính đến tháng 9 năm 2023, Tháp Khách sạn Diamond Crown Hai Phong (tháp B) là tòa nhà cao nhất Hải Phòng với 186 mét, được c

جورج أولاه (بالإنجليزية: George Andrew Olah)، و(بالمجرية: Oláh György) معلومات شخصية اسم الولادة (بالمجرية: Oláh András György) الميلاد 22 مايو 1927[1][2] بودابست الوفاة 8 مارس 2017 (89 سنة) [3][1] بيفرلي هيلز، كاليفورنيا[4] مواطنة المجر الولايات المتحدة �...

第三十一届夏季奧林匹克運動會男子單槓比賽比賽場館里約奧林匹克體育館日期8月16日参赛选手8位選手,來自7個國家和地區奖牌获得者01 ! 法比安·汉布钦 德国02 ! 丹內爾·萊瓦 美国03 ! 尼爾·威爾森 英国← 20122020 → 2016年夏季奧林匹克運動會體操比賽 參賽運動員名單 競技體操 資格賽 男子 女子 團體賽 男子 女子 個�...

Fewest graph edges whose removal breaks all cycles For related notion called cycle rank in directed graphs, see cycle rank. This graph has circuit rank r = 2 because it can be made into a tree by removing two edges, for instance the edges 1–2 and 2–3, but removing any one edge leaves a cycle in the graph. In graph theory, a branch of mathematics, the circuit rank, cyclomatic number, cycle rank, or nullity of an undirected graph is the minimum number of edges that must be removed from the ...

Indonesian TV presenter, actor, YouTuber and mentalist (born 1976) In this Chinese Indonesian name, the family name is Sunjoyo. Lieutenant Colonel (Tit.)Deddy CorbuzierDeddy as a co-host in Ini Talkshow at NET.Born (1976-12-28) 28 December 1976 (age 46)Jakarta, IndonesiaOccupationsMagicianPresenterCelebrityMentallistYears active1998–2015 (as magician)2000–present (as presenter)Spouse Kalina Oktarani (m. 2005; div. 2013) Sabrina...

Batman: Arkham City is a 2011 action-adventure video game based on the DC Comics superhero Batman. Two music albums were released alongside the game: Batman: Arkham City – Original Video Game Score which contains the game's original score by Nick Arundel and Ron Fish and Batman: Arkham City – The Album containing songs by various mainstream artists. Batman: Arkham City – Original Video Game Score Batman: Arkham City – Original Video Game ScoreFilm score by Nick Arundel and Ron Fis...

1947 film CoincidencesDirected bySerge DebecqueWritten bySerge Debecque Pierre LarocheProduced byJean Jeannin Jules SuchanekStarringSerge Reggiani Andrée Clément Pierre RenoirCinematographyJean IsnardEdited byMarity ClérisMusic byGermaine TailleferreProductioncompanyEquipes Artisanales CinématographiquesDistributed byLux Compagnie Cinématographique de FranceRelease date15 October 1947Running time95 minutesCountryFranceLanguageFrench Coincidences (French: Coïncidences) is a 1947 French d...

Sporting event delegation Sporting event delegationSaint Kitts and Nevis at the2020 Summer OlympicsFlag of Saint Kitts and NevisIOC codeSKNNOCSaint Kitts and Nevis Olympic CommitteeWebsitewww.sknoc.orgin Tokyo, Japan23 July 2021 (2021-07-23) – August 8, 2021 (2021-08-08)Competitors2 in 1 sportFlag bearers (opening)Amya ClarkeJason RogersFlag bearer (closing)N/AMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)199620002...

Botanical garden in Hampshire, England Exbury GardensHerbaceous borders near the houseLocation in HampshireLocationNew ForestCoordinates50°47′55″N 1°24′02″W / 50.7986°N 1.4005°W / 50.7986; -1.4005Created1919Operated byExbury Gardens LimitedDesignationGrade II* Exbury Gardens is a 200-acre (81 ha) informal woodland garden in Hampshire, England with large collections of rhododendrons, azaleas and camellias, and is often considered the finest garden ...

Irish television channel group For Eir Sport 1 and Eir Sport 2, see Eir Sport 1 and Eir Sport 2. Television channel Eir SportOwnershipOwnerEirHistoryFormer namesSetanta Sports (2007-2016)LinksWebsitewww.eirsport.ie Eir Sport (stylised as eir Sport; formerly Setanta Sports) was a group of Irish television sports channels operated by Eircom Sport Limited, a subsidiary of Eir.[1] In December 2015, Eir purchased original Setanta Sports operations in the Republic of Ireland,[2] whi...

1948 film AnniGerman film posterDirected byMax NeufeldWritten byHarald RöbbelingMax NeufeldProduced byHeinrich HaasStarringElfie MayerhoferSiegfried BreuerJosef MeinradElisabeth MarkusCinematographyWalter RimlMusic byAlois MelicharProductioncompanyStyria-Berna-FilmDistributed bySchorcht FilmverleihRelease date 4 June 1948 (1948-06-04) Running time93 minutesCountriesAustriaGermanyLanguageGerman Anni is a 1948 Austrian-German historical romance film directed by Max Neufeld and s...

Brandon Lyon Lyon con la maglia dei Blue Jays Nazionalità Stati Uniti Altezza 185 cm Peso 91 kg Baseball Ruolo Lanciatore di rilievo Squadra free agnet Termine carriera 4 luglio 2013 Carriera Squadre di club 2001 - 2002 Toronto Blue Jays2003 Boston Red Sox2005 - 2008 Arizona Diamondbacks2009 Detroit Tigers2010 - 2012 Houston Astros2012 Toronto Blue Jays2013 New York Mets Statistiche Batte destro Lancia destro Basi su ball 220 Strikeout 465 Punti conce...

American politician William V. MarquisLieutenant Governor of OhioIn office1890–1892GovernorJames E. Campbell Personal detailsBorn(1828-05-01)May 1, 1828Mt. Vernon, OhioDiedDecember 17, 1899(1899-12-17) (aged 71)Spouse Annie M. Sterritt (m. 1860; died 1868) William Vance Marquis (May 1, 1828 – December 17, 1899)[1] was an American politician who served as the 22nd lieutenant governor of Ohio from 1890 to 1892 under Governor J...

邓发中共中央党校校长任期1939年-1943年3月 个人资料性别男别名邓元钊(原名)出生1906年3月7日 清朝广东省云浮县附城乡石塘村逝世1946年4月8日(1946歲—04—08)(40歲) 中華民國山西省兴县黑茶山上空籍贯中国广东省云浮云城区政党 中国共产党配偶陈慧清亲属子:邓北生 学历 小学 经历 香港海员罢工省港大罢工北伐战争广州暴动中共香港市委书记闽粤赣苏区特委�...