Star polygon
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

För den finländske diplomaten och författaren, se René Nyberg (diplomat). Renée Nyberg Renée Nyberg på Kristallen-galan 2013.Född17 maj 1966 (57 år)Vantörs församling, Stockholm, SverigeNationalitetSvenskYrke/uppdragProgramledareÅr som aktiv1992–Känd förRenées bryggaMakeDavid Hellenius (2009– )Barn3 Renée Nyberg besöker Sommarkrysset 2009. Eva Renée Agneta Nyberg,[a] född 17 maj 1966 i Vantörs församling i Stockholm,[1] är en svensk programl...

Mniejszość seksualna Mniejszość seksualna – odsetek społeczeństwa o orientacji seksualnej innej, niż dominująca statystycznie. Według różnych szacunków od 1% do 21% populacji USA jest orientacji homoseksualnej lub biseksualnej[1]. Badania przeprowadzone w roku 1970 w Stanach Zjednoczonych wykazały, że około 20% dorosłych mężczyzn miało kontakt z mężczyzną prowadzący do orgazmu, jednak tylko 6,7% po 19 roku życia i kontakty połowy z 6,7% były rzadkie[2]. Przykładem...

Mallemort Mallemort (Frankreich) Staat Frankreich Region Provence-Alpes-Côte d’Azur Département (Nr.) Bouches-du-Rhône (13) Arrondissement Aix-en-Provence Kanton Pélissanne Gemeindeverband Métropole d’Aix-Marseille-Provence Koordinaten 43° 44′ N, 5° 11′ O43.7316666666675.1802777777778Koordinaten: 43° 44′ N, 5° 11′ O Höhe 99–225 m Fläche 28,16 km² Einwohner 6.184 (1. Januar 2020) Bevölkerungsdichte 220 Einw./km²...

American politician John C. MackieMember of the U.S. House of Representativesfrom Michigan's 7th districtIn officeJanuary 3, 1965 – January 3, 1967Preceded byJames G. O'HaraSucceeded byDonald Riegle9th Michigan State Highway CommissionerIn officeJuly 1, 1957 – January 4, 1965GovernorG. Mennen WilliamsJohn SwainsonGeorge W. RomneyPreceded byCharles M. ZieglerSucceeded byOffice abolished(Howard E. Hill, first MDSH Director) Personal detailsBorn(1920-06-01)June ...

Erwanto KurniadiInformasi pribadiLahirApril 1967JakartaMeninggal17 Mei 2019JakartaKarier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik IndonesiaMasa dinas1989–2019Pangkat Brigadir Jenderal PolisiSatuanReserseSunting kotak info • L • B Brigjen Pol. (Purn.) Drs. Erwanto Kurniadi, S.H., M.H. (lahir di Jakarta, April 1967 – meninggal di Jakarta, 17 Mei 2019) adalah seorang perwira tinggi Polri yang terakhir kali sebelum meninggal menjabat sebagai Dirtip...

Henning Schulzrinne Schulzrinne at the SIPNOC 2012.Información personalNacimiento Siglo XX Colonia, AlemaniaNacionalidad AlemanaEducaciónEducado en Universidad de ColumbiaSupervisor doctoral Jim Kurose Información profesionalÁrea Redes informáticasConocido por RTSP, SIPEmpleador Universidad de Columbia Obras notables Session Initiation ProtocolReal-time Transport Protocol Sitio web www.cs.columbia.edu/~hgs Distinciones Salón de la Fama de Internet (2013)ACM Fellow (2014) ...

المحكمة الدستورية لروسيا الاتحادية تعديل مصدري - تعديل 59°56′07″N 30°18′05″E / 59.93528°N 30.30139°E / 59.93528; 30.30139 جزء من سلسلة مقالات سياسة روسياروسيا الدستور الدستور حقوق الإنسان السلطة التنفيذية الرئيس مجلس الوزراء الحكومة السلطة التشريعية الجمعية الاتحادية مجلس ال�...

الحبيبات الفائقة في الكروموسفير للشمس الحبيبات الشمسية الفائقة هو نمط معين من خلايا الحمل الحراري على سطح الشمس. اكتشف في سنة 1950 من قبل أجهزة تستعمل قياسات سرعة دوبلر والتي أظهرت تدفقات أفقية على الغلاف الضوئي (سرعة التدفق نحو 300 إلى 500 متر / ثانية). أظهرت أعمال لاحقة في سنة 19...

United States historic placeJordan Village Historic DistrictU.S. National Register of Historic PlacesU.S. Historic district The 1838 Beebe Phillips house (left) and the 1740 Jordan Schoolhouse on Jordan GreenShow map of ConnecticutShow map of the United StatesLocationJunction of North Rd. and Avery Ln. with Rope Ferry Rd., Waterford, ConnecticutCoordinates41°20′23″N 72°8′33″W / 41.33972°N 72.14250°W / 41.33972; -72.14250Area57 acres (23 ha)Built1848Arc...

1959 film by B. R. Panthulu For the 1993 film, see Kattabomman (film). Veerapandiya KattabommanTheatrical release posterDirected byB. R. PanthuluStory bySakthi T. K. KrishnasamyBased onVeerapandiya Kattabomman (play)Produced byB. R. PanthuluStarring Sivaji Ganesan Gemini Ganesan Padmini S. Varalakshmi Ragini CinematographyW. R. SubbaraoEdited byR. DevarajanMusic byG. RamanathanProductioncompanyPadmini PicturesDistributed bySivaji FilmsRelease dates 10 May 1959 (1959-05-10) ...

The Most HonourableThe Marquess of LinlithgowKT GCMG GCVO PCGubernur Jenderal Australia ke-1Masa jabatan1 Januari 1901 – 17 Juli 1902Penguasa monarkiVictoriaEdward VIIPerdana MenteriEdmund BartonPendahuluPosisi baruPenggantiLord TennysonGubernur Victoria ke-7Masa jabatan28 November 1889 – 12 Juli 1895Perdana MenteriDuncan Gillies James Munro William Shiels James Patterson George TurnerPendahuluLord LochPenggantiLord BrasseySekretaris SkotlandiaMasa jabatan2 Febru...
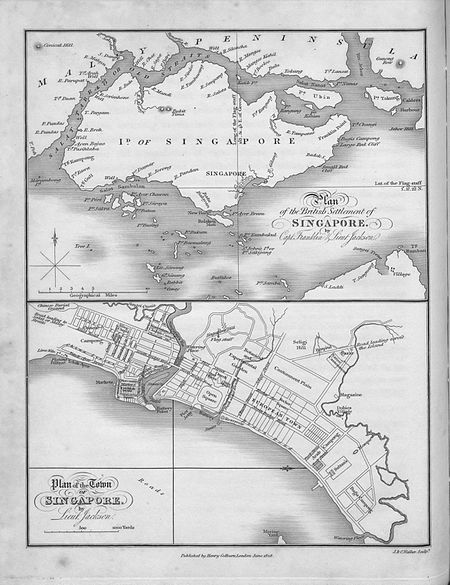
Malay island kingdom For the current republic, see Singapore. Kingdom of SingapuraKerajaan Singapura1299–1398Kingdom of Singapore, with ruins of an old wall still visible in 1825 and marked on this map.CapitalSingapura[1]Common languagesOld MalayReligion Syncretic forms of Hinduism and BuddhismGovernmentMonarchyRaja • 1299–1347 Sang Nila Utama (Sri Tri Buana)• 1347–1362 Sri Wikrama Wira• 1362–1375 Sri Rana Wikrama• 1375–1389 Sri Maharaja...

Distribuição de NRHPs nos condados de Indiana. Edifícios, locais, distritos e objetos no Registro Nacional de Lugares Históricos en Indiana. Desde 7 de fevereiro de 2014[1] existem 1 822 propriedades e distritos do Registro Nacional de Lugares Históricos listados nos 92 condados de Indiana, incluindo os 39 nomeados no Marco Histórico Nacional. O condado de Marion é o que contem a maior quantidade de registros, enquanto outros três condados possuem apenas um registro cada um. Os p...

This article is about the comedy film from 1995 in the United States. For other uses, see House guest (disambiguation). 1995 American filmHouseguestPromotional movie posterDirected byRandall MillerWritten byMichael J. Di GaetanoLawrence GayProduced byJoe RothRoger BirnbaumStarring Sinbad Phil Hartman Jeffrey Jones Kim Greist CinematographyJerzy ZielinskiEdited byEric SearsMusic byJohn DebneyProductioncompaniesHollywood PicturesCaravan PicturesDistributed byBuena Vista Pictures DistributionRel...

Jehanabad Assembly constituencyConstituency No. 216 for the Bihar Legislative AssemblyConstituency detailsCountryIndiaRegionEast IndiaStateBiharDistrictJehanabadLS constituency36 JehanabadMember of Legislative Assembly17th Bihar Legislative AssemblyIncumbent Suday Yadav PartyRashtriya Janata DalElected year2020 Assembly constituency in Bihar, India Jehanabad Assembly constituency is an assembly constituency in Jehanabad district and South Bihar region of Bihar. It is the part of Jahanabad (Lo...

This article provides insufficient context for those unfamiliar with the subject. Please help improve the article by providing more context for the reader. (June 2017) (Learn how and when to remove this template message) 2017 USAC National Midget Series Previous 2016 Next 2018 champion Spencer Bayston The 2017 USAC National Midget Series is the 62nd season of the USAC National Midget Series. The series began with the Shamrock Classic at Southern Illinois Center on March 18, and will end with ...

A studio founded by Walt Disney Laugh-O-Gram StudioMcConahay Films Building in August 2010IndustryFilm studioPredecessorsIwerks-Disney Commercial ArtistsFoundedJune 28, 1921; 102 years ago (June 28, 1921)FounderWalt DisneyDefunctOctober 16, 1923; 100 years ago (October 16, 1923)FateBankruptcySuccessorsDisney Brothers Cartoon StudioHeadquarters Kansas City, Missouri 39°04′13″N 94°34′12″W / 39.070362°N 94.56994°W / 39.070362; -94.569...

1986 film by Blake Edwards This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: That's Life! film – news · newspapers · books · scholar · JSTOR (February 2016) (Learn how and when to remove this template message) That's Life!Theatrical release posterDirected byBlake EdwardsWritten byBlake EdwardsMilton Wexle...

Football clubMartos CDFull nameMartos Club DeportivoFounded1970GroundEstadio Municipal Ciudad de Martos Martos, SpainCapacity5,000ManagerFernando CamposLeagueDivisión de Honor Andaluza – Group 22022–23División de Honor Andaluza – Group 2, 8th Home colours Away colours Martos Club Deportivo is a Spanish football club, founded in 1970 and based in Martos. The club competes in División de Honor Andaluza, holding home games at the Estadio Municipal Ciudad de Martos, with a capacity of 5,...

2003 compilation album by Ghostface KillahShaolin's FinestCompilation album by Ghostface KillahReleasedApril 1, 2003 [1]Recorded1996-2001GenreHip hop[2]Length47:00LabelEpic[1]Ghostface Killah chronology Bulletproof Wallets(2001) Shaolin's Finest(2003) 718(2004) Professional ratingsReview scoresSourceRatingAllMusic [3]Spin(6/10) [4] Shaolin's Finest is a compilation album by American rapper Ghostface Killah, featuring singles from the albums Iron...
































