–Я—А–Є–Ї–ї–∞–і –њ—А–Њ—Б—В–Њ—Ч –њ–Њ–≤–µ—А—Е–љ—Ц –Я–Њ–≤–µ—А—Е–љ—П –≤ –Љ–∞—В–µ–Љ–∞—В–Є—Ж—Ц, –Њ—Б–Њ–±–ї–Є–≤–Њ –≤ —В–Њ–њ–Њ–ї–Њ–≥—Ц—Ч , —Ж–µ –і–≤–Њ–≤–Є–Љ—Ц—А–љ–Є–є —В–Њ–њ–Њ–ї–Њ–≥—Ц—З–љ–Є–є –Љ–љ–Њ–≥–Њ–≤–Є–і .
–Э–∞–є–≤—Ц–і–Њ–Љ—Ц—И–Є–Љ–Є –њ—А–Є–Ї–ї–∞–і–∞–Љ–Є —Ф —В—Ц, —Й–Њ –≤–Є–љ–Є–Ї–∞—О—В—М —П–Ї –Љ–µ–ґ–∞ —В—Ц–ї–∞ —Г –Ј–≤–Є—З–∞–є–љ–Њ–Љ—Г —В—А–Є–≤–Є–Љ—Ц—А–љ–Њ–Љ—Г –µ–≤–Ї–ї—Ц–і–Њ–≤–Њ–Љ—Г –њ—А–Њ—Б—В–Њ—А—Ц R 3 . –Э–∞–њ—А–Є–Ї–ї–∞–і, —Ж–µ –њ–Њ–≤–µ—А—Е–љ—П –Ї—Г–ї—Ц . –Ч —Ц–љ—И–Њ–≥–Њ –±–Њ–Ї—Г, —Ф –њ–Њ–≤–µ—А—Е–љ—Ц, —В–∞–Ї—Ц —П–Ї –њ–ї—П—И–Ї–∞ –Ъ–ї–µ–є–љ–∞ , —П–Ї—Ц –љ–µ –Љ–Њ–ґ—Г—В—М –±—Г—В–Є –≤–Ї–ї–∞–і–µ–љ–Є–Љ–Є –≤ —В—А–Є–≤–Є–Љ—Ц—А–љ–Є–є –µ–≤–Ї–ї—Ц–і—Ц–≤ –њ—А–Њ—Б—В—Ц—А –±–µ–Ј –Њ—Б–Њ–±–ї–Є–≤–Њ—Б—В–µ–є –∞–±–Њ —Б–∞–Љ–Њ–њ–µ—А–µ—В–Є–љ—Ц–≤.
–Ъ–Њ–ї–Є –Ї–∞–ґ—Г—В—М, —Й–Њ –њ–Њ–≤–µ—А—Е–љ—П —Ф ¬Ђ–і–≤–Њ–≤–Є–Љ—Ц—А–љ–Њ—О¬ї, —В–Њ —Ж–µ –Њ–Ј–љ–∞—З–∞—Ф, —Й–Њ —Г –Ї–Њ–ґ–љ–Њ—Ч —В–Њ—З–Ї–Є —Ц—Б–љ—Г—Ф –Њ–Ї—Ц–ї —П–Ї–Є–є –Љ–Њ–ґ–љ–∞ –≤—Ц–і–Њ–±—А–∞–Ј–Є—В–Є –±–µ–Ј —А–Њ–Ј—А–Є–≤—Г –љ–∞ –і–≤–Њ–≤–Є–Љ—Ц—А–љ–Є–є –Ї—А—Г–≥ .
–Я–Њ–љ—П—В—В—П –њ–Њ–≤–µ—А—Е–љ—Ц –≤–Є–Ї–Њ—А–Є—Б—В–Њ–≤—Г—Ф—В—М—Б—П —Г —Д—Ц–Ј–Є—Ж—Ц , –±—Г–і—Ц–≤–љ–Є—Ж—В–≤—Ц , –Ї–Њ–Љ–њ'—О—В–µ—А–љ—Ц–є –≥—А–∞—Д—Ц—Ж—Ц —Ц –±–∞–≥–∞—В—М–Њ—Е —Ц–љ—И–Є—Е –≥–∞–ї—Г–Ј—П—Е, —П–Ї—Ц –Љ–∞—О—В—М —Б–њ—А–∞–≤—Г –Ј –њ–Њ–≤–µ—А—Е–љ—П–Љ–Є —Д—Ц–Ј–Є—З–љ–Є—Е –Њ–±'—Ф–Ї—В—Ц–≤. –Э–∞–њ—А–Є–Ї–ї–∞–і, –њ—Ц–і —З–∞—Б –∞–љ–∞–ї—Ц–Ј—Г –∞–µ—А–Њ–і–Є–љ–∞–Љ—Ц—З–љ–Є—Е –≤–ї–∞—Б—В–Є–≤–Њ—Б—В–µ–є –ї—Ц—В–∞–Ї–∞ , –њ–µ—А—И –Ј–∞ –≤—Б–µ, –Ј–≤–µ—А—В–∞—О—В—М —Г–≤–∞–≥—Г –љ–∞ –њ–Њ—В—Ц–Ї –њ–Њ–≤—Ц—В—А—П —Г–Ј–і–Њ–≤–ґ –є–Њ–≥–Њ –њ–Њ–≤–µ—А—Е–љ—Ц.
–Т —В—А–Є–≤–Є–Љ—Ц—А–љ–Њ–Љ—Г –њ—А–Њ—Б—В–Њ—А—Ц –њ–Њ–≤–µ—А—Е–љ—О –Љ–Њ–ґ–љ–∞ –≤–Є–Ј–љ–∞—З–Є—В–Є –љ–µ—П–≤–љ–Њ, —П–Ї –Љ–љ–Њ–ґ–Є–љ—Г —В–Њ—З–Њ–Ї , –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є —П–Ї–Є—Е –Ј–∞–і–Њ–≤–Њ–ї—М–љ—П—О—В—М –њ–µ–≤–љ–Њ–Љ—Г –≤–Є–і—Г —А—Ц–≤–љ—П–љ—М:
F
(
x
,
y
,
z
)
=
0
(
1
)
{\displaystyle F(x,\,y,\,z)=0\qquad (1)}
–ѓ–Ї—Й–Њ —Д—Г–љ–Ї—Ж—Ц—П
F
(
x
,
y
,
z
)
{\displaystyle F(x,\,y,\,z)}
–љ–µ–њ–µ—А–µ—А–≤–љ–∞ –≤ –і–µ—П–Ї—Ц–є —В–Њ—З—Ж—Ц —Ц –Љ–∞—Ф –≤ –љ—Ц–є –љ–µ–њ–µ—А–µ—А–≤–љ—Ц —З–∞—Б—В–Ї–Њ–≤—Ц –њ–Њ—Е—Ц–і–љ—Ц, –њ—А–Є–љ–∞–є–Љ–љ—Ц –Њ–і–љ–∞ –Ј —П–Ї–Є—Е –љ–µ –њ–µ—А–µ—В–≤–Њ—А—О—Ф—В—М—Б—П –љ–∞ –љ—Г–ї—М, —В–Њ –≤ –Њ–Ї–Њ–ї—Ц —Ж—Ц—Ф—Ч —В–Њ—З–Ї–Є –њ–Њ–≤–µ—А—Е–љ—П, –Ј–∞–і–∞–љ–∞ —А—Ц–≤–љ—П–љ–љ—П–Љ (1), –±—Г–і–µ –њ—А–∞–≤–Є–ї—М–љ–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О .
–Э–∞ –≤—Ц–і–Љ—Ц–љ—Г –≤—Ц–і –љ–µ—П–≤–љ–Њ–≥–Њ —Б–њ–Њ—Б–Њ–±—Г –Ј–∞–і–∞–љ–љ—П, –њ–Њ–≤–µ—А—Е–љ—П –Љ–Њ–ґ–µ –±—Г—В–Є –≤–Є–Ј–љ–∞—З–µ–љ–∞ —П–≤–љ–Њ, —П–Ї—Й–Њ –Њ–і–љ—Г –Ј—Ц –Ј–Љ—Ц–љ–љ–Є—Е, –љ–∞–њ—А–Є–Ї–ї–∞–і z, –Љ–Њ–ґ–љ–∞ –≤–Є—А–∞–Ј–Є—В–Є —З–µ—А–µ–Ј —Ц–љ—И—Ц:
z
=
f
(
x
,
y
)
(
1
′
)
{\displaystyle z=f(x,y)\qquad (1')}
–Ґ–∞–Ї–Њ–ґ —Ц—Б–љ—Г—Ф –њ–∞—А–∞–Љ–µ—В—А–Є—З–љ–Є–є —Б–њ–Њ—Б—Ц–± –Ј–∞–і–∞–љ–љ—П. –£ —Ж—М–Њ–Љ—Г –≤–Є–њ–∞–і–Ї—Г –њ–Њ–≤–µ—А—Е–љ—П –≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П —Б–Є—Б—В–µ–Љ–Њ—О —А—Ц–≤–љ—П–љ—М:
{
x
=
x
(
u
,
v
)
y
=
y
(
u
,
v
)
z
=
z
(
u
,
v
)
(
1
″
)
{\displaystyle \left\{{\begin{array}{ccc}x&=&x(u,v)\\y&=&y(u,v)\\z&=&z(u,v)\end{array}}\right.\qquad (1'')}
–ѓ–≤–љ–µ —В–∞ –љ–µ—П–≤–љ–µ —А—Ц–≤–љ—П–љ–љ—П –њ–ї–Њ—Й–Є–љ–Є –≤ E 3 , —П–Ї–∞ –Ј–±—Ц–≥–∞—Ф—В—М—Б—П –Ј –њ–ї–Њ—Й–Є–љ–Њ—О Oxy z=0
–Я–∞—А–∞–Љ–µ—В—А–Є—З–љ–µ —А—Ц–≤–љ—П–љ–љ—П —В—Ц—Ф—Ч –ґ –њ–ї–Њ—Й–Є–љ–Є:
{
x
=
u
y
=
v
z
=
0
,
u
,
v
∈ вИИ -->
R
.
{\displaystyle \left\{{\begin{array}{ccc}x&=&u\\y&=&v\\z&=&0\end{array}}\right.,\quad u,v\in \mathbb {R} .}
–Э–µ—П–≤–љ–µ —А—Ц–≤–љ—П–љ–љ—П —Б—Д–µ—А–Є –Њ–і–Є–љ–Є—З–љ–Њ–≥–Њ —А–∞–і—Ц—Г—Б–∞ –Ј —Ж–µ–љ—В—А–Њ–Љ —Г –њ–Њ—З–∞—В–Ї—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В –≤ E 3 вАФ
x
2
+
y
2
+
z
2
=
1
{\displaystyle x^{2}+y^{2}+z^{2}=1}
–ѓ–≤–љ–µ –Ј–∞–і–∞–љ–љ—П —Б—Д–µ—А–Є –Њ–і–љ–Є–Љ —А—Ц–≤–љ—П–љ–љ—П–Љ –љ–µ–Љ–Њ–ґ–ї–Є–≤–µ. –Ь–Њ–ґ–љ–∞ —П–≤–љ–Њ –Њ–њ–Є—Б–∞—В–Є –і–≤—Ц –њ—Ц–≤—Б—Д–µ—А–Є вАФ
z
=
± ¬± -->
1
− вИТ -->
x
2
− вИТ -->
y
2
{\displaystyle z=\pm {\sqrt {1-x^{2}-y^{2}}}}
–Я–∞—А–∞–Љ–µ—В—А–Є—З–љ–µ —А—Ц–≤–љ—П–љ–љ—П —Б—Д–µ—А–Є:
{
x
=
sin
вБ° -->
v
cos
вБ° -->
u
y
=
sin
вБ° -->
v
sin
вБ° -->
u
z
=
cos
вБ° -->
v
,
0
⩽ в©љ -->
u
<
2
π ѕА -->
,
0
⩽ в©љ -->
v
⩽ в©љ -->
π ѕА -->
.
{\displaystyle \left\{{\begin{array}{ccc}x&=&\sin v\;\cos u\\y&=&\sin v\;\sin u\\z&=&\cos v\end{array}}\right.,\quad 0\leqslant u<2\pi ,\ 0\leqslant v\leqslant \pi .}
–Ж–љ—В—Г—Ч—В–Є–≤–љ–Њ –њ—А–Њ—Б—В—Г –њ–Њ–≤–µ—А—Е–љ—О –Љ–Њ–ґ–љ–∞ —Г—П–≤–Є—В–Є —П–Ї —И–Љ–∞—В–Њ–Ї –њ–ї–Њ—Й–Є–љ–Є , –њ—Ц–і–і–∞–љ–Є–є –љ–µ–њ–µ—А–µ—А–≤–љ–Є–Љ –і–µ—Д–Њ—А–Љ–∞—Ж—Ц—П–Љ (—А–Њ–Ј—В—П–≥—Г–≤–∞–љ—П–Љ, —Б—В–Є—Б–Ї–∞–љ–љ—П–Љ —Ц –Ј–≥–Є–љ–∞–љ–љ—П–Љ ).
–С—Ц–ї—М—И —Б—В—А–Њ–≥–Њ, –њ—А–Њ—Б—В–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О –≥–Њ–Љ–µ–Њ–Љ–Њ—А—Д–љ–Њ–≥–Њ –≤—Ц–і–Њ–±—А–∞–ґ–µ–љ–љ—П (—В–Њ–±—В–Њ –≤–Ј–∞—Ф–Љ–љ–Њ –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ–≥–Њ —В–∞ –≤–Ј–∞—Ф–Љ–љ–Њ –љ–µ–њ–µ—А–µ—А–≤–љ–Њ–≥–Њ –≤—Ц–і–Њ–±—А–∞–ґ–µ–љ–љ—П) –≤–љ—Ц—В—А—Ц—И–љ—Ц—Е —В–Њ—З–Њ–Ї –Њ–і–Є–љ–Є—З–љ–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞. –¶–µ –≤–Є–Ј–љ–∞—З–µ–љ–љ—О –Љ–Њ–ґ–љ–∞ –≤–Є—А–∞–Ј–Є—В–Є –∞–љ–∞–ї—Ц—В–Є—З–љ–Њ .
–Э–µ—Е–∞–є –љ–∞ –њ–ї–Њ—Й–Є–љ—Ц –Ј –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ—О —Б–Є—Б—В–µ–Љ–Њ—О –Ї–Њ–Њ—А–і–Є–љ–∞—В u —Ц v –Ј–∞–і–∞–љ–Њ –Ї–≤–∞–і—А–∞—В , –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є –≤–љ—Г—В—А—Ц—И–љ—Ц—Е —В–Њ—З–Њ–Ї —П–Ї–Њ–≥–Њ –Ј–∞–і–Њ–≤–Њ–ї—М–љ—П—О—В—М –љ–µ—А—Ц–≤–љ–Њ—Б—В—П–Љ 0 < u < 1, 0 < v < 1. –У–Њ–Љ–µ–Њ–Љ–Њ—А—Д–љ–Є–є –Њ–±—А–∞–Ј –Ї–≤–∞–і—А–∞—В–∞ —Г –њ—А–Њ—Б—В–Њ—А—Ц –Ј –њ—А—П–Љ–Њ–Ї—Г—В–љ–Њ—О —Б–Є—Б—В–µ–Љ–Њ—О –Ї–Њ–Њ—А–і–Є–љ–∞—В —Е, —Г, z –Ј–∞–і–∞—Ф—В—М—Б—П –Ј–∞ –і–Њ–њ–Њ–Љ–Њ–≥–Њ—О —Д–Њ—А–Љ—Г–ї —Е = x(u, v), —Г = y(u, v), z = z(u, v) (–њ–∞—А–∞–Љ–µ—В—А–Є—З–љ–µ –Ј–∞–і–∞–љ–љ—П –њ–Њ–≤–µ—А—Е–љ—Ц ). –Я—А–Є —Ж—М–Њ–Љ—Г –≤—Ц–і —Д—Г–љ–Ї—Ж—Ц–є x(u, v), y(u, v) —Ц z(u, v) –≤–Є–Љ–∞–≥–∞—Ф—В—М—Б—П, —Й–Њ–± –≤–Њ–љ–Є –±—Г–ї–Є –љ–µ–њ–µ—А–µ—А–≤–љ–Є–Љ–Є —Ц —Й–Њ–± –і–ї—П —А—Ц–Ј–љ–Є—Е —В–Њ—З–Њ–Ї (u, v) —Ц (u', v') –±—Г–ї–Є —А—Ц–Ј–љ–Є–Љ–Є –≤—Ц–і–њ–Њ–≤—Ц–і–љ—Ц —В–Њ—З–Ї–Є (x, —Г, z) —Ц (x', —Г', z').
–Я—А–Є–Ї–ї–∞–і–Њ–Љ –њ—А–Њ—Б—В–Њ—Ч –њ–Њ–≤–µ—А—Е–љ—Ц —Ф –њ—Ц–≤—Б—Д–µ—А–∞. –Т—Б—П –ґ —Б—Д–µ—А–∞ –љ–µ —Ф –њ—А–Њ—Б—В–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О . –¶–µ –≤–Є–Ї–ї–Є–Ї–∞—Ф –љ–µ–Њ–±—Е—Ц–і–љ—Ц—Б—В—М –њ–Њ–і–∞–ї—М—И–Њ–≥–Њ —Г–Ј–∞–≥–∞–ї—М–љ–µ–љ–љ—П –њ–Њ–љ—П—В—В—П –њ–Њ–≤–µ—А—Е–љ—Ц.
–Я—Ц–і–Љ–љ–Њ–ґ–Є–љ–∞ –њ—А–Њ—Б—В–Њ—А—Г, —Г –Ї–Њ–ґ–љ–Њ—Ч —В–Њ—З–Ї–Є —П–Ї–Њ–≥–Њ —Ф –Њ–Ї—Ц–ї, —Й–Њ —Ф –њ—А–Њ—Б—В–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О , –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –њ—А–∞–≤–Є–ї—М–љ–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О
–Т –і–Є—Д–µ—А–µ–љ—Ж—Ц–∞–ї—М–љ–Њ—Ч –≥–µ–Њ–Љ–µ—В—А—Ц—Ч –і–Њ—Б–ї—Ц–і–ґ—Г–≤–∞–љ—Ц –њ–Њ–≤–µ—А—Е–љ—Ц –Ј–∞–Ј–≤–Є—З–∞–є –њ—Ц–і–њ–Њ—А—П–і–Ї–Њ–≤–∞–љ—Ц —Г–Љ–Њ–≤–∞–Љ, –њ–Њ–≤'—П–Ј–∞–љ–Є–Љ –Ј –Љ–Њ–ґ–ї–Є–≤—Ц—Б—В—О –Ј–∞—Б—В–Њ—Б—Г–≤–∞–љ–љ—П –Љ–µ—В–Њ–і—Ц–≤ –і–Є—Д–µ—А–µ–љ—Ж—Ц–∞–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–µ–љ–љ—П. –ѓ–Ї –њ—А–∞–≤–Є–ї–Њ, —Ж–µ —Г–Љ–Њ–≤–Є –≥–ї–∞–і–Ї–Њ—Б—В—Ц –њ–Њ–≤–µ—А—Е–љ—Ц, —В–Њ–±—В–Њ —Ц—Б–љ—Г–≤–∞–љ–љ—П –≤ –Ї–Њ–ґ–љ—Ц–є —В–Њ—З—Ж—Ц –њ–Њ–≤–µ—А—Е–љ—Ц –њ–µ–≤–љ–Њ—Ч –і–Њ—В–Є—З–љ–Њ—Ч –њ–ї–Њ—Й–Є–љ–Є, –Ї—А–Є–≤–Є–љ–Є —В–Њ—Й–Њ. –¶—Ц –≤–Є–Љ–Њ–≥–Є –Ј–≤–Њ–і—П—В—М—Б—П –і–Њ —В–Њ–≥–Њ, —Й–Њ —Д—Г–љ–Ї—Ж—Ц—Ч, —Й–Њ –Ј–∞–і–∞—О—В—М –њ–Њ–≤–µ—А—Е–љ—О, –Љ–∞—О—В—М –±—Г—В–Є –Њ–і–љ–Њ—А–∞–Ј–Њ–≤–Њ, –і–≤—Ц—З—Ц, —В—А–Є—З—Ц, –∞ –≤ –і–µ—П–Ї–Є—Е –≤–Є–њ–∞–і–Ї–∞—Е вАФ –љ–µ–Њ–±–Љ–µ–ґ–µ–љ—Г –Ї—Ц–ї—М–Ї—Ц—Б—В—М —А–∞–Ј—Ц–≤ –і–Є—Д–µ—А–µ–љ—Ж—Ц–є–Њ–≤–љ–Є–Љ–Є –∞–±–Њ –љ–∞–≤—Ц—В—М –∞–љ–∞–ї—Ц—В–Є—З–љ–Є–Љ–Є —Д—Г–љ–Ї—Ж—Ц—П–Љ–Є . –Я—А–Є —Ж—М–Њ–Љ—Г –і–Њ–і–∞—В–Ї–Њ–≤–Њ –љ–∞–Ї–ї–∞–і–∞—Ф—В—М—Б—П —Г–Љ–Њ–≤–∞ —А–µ–≥—Г–ї—П—А–љ–Њ—Б—В—Ц.
–Т–Є–њ–∞–і–Њ–Ї –љ–µ—П–≤–љ–Њ–≥–Њ –Ј–∞–і–∞–љ–љ—П. –Я–Њ–≤–µ—А—Е–љ—П, –Ј–∞–і–∞–љ–∞ —А—Ц–≤–љ—П–љ–љ—П–Љ
F
(
x
,
y
,
z
)
=
0
,
F
:
Ω ќ© -->
→ вЖТ -->
R
3
{\displaystyle F(x,\,y,\,z)=0,\;F:\Omega \to \mathbb {R} ^{3}}
–≥–ї–∞–і–Ї–Њ—О —А–µ–≥—Г–ї—П—А–љ–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О , —П–Ї—Й–Њ:
∃ вИГ -->
P
0
(
x
0
,
y
0
,
z
0
)
:
F
(
x
0
,
y
0
,
z
0
)
=
0
{\displaystyle \exists P_{0}(x_{0},\,y_{0},\,z_{0}):\;F(x_{0},\,y_{0},\,z_{0})=0}
F
{\displaystyle F}
–љ–µ–њ–µ—А–µ—А–≤–љ–Њ –і–Є—Д–µ—А–µ–љ—Ж—Ц–є–Њ–≤–љ–∞ –≤ —Б–≤–Њ—Ч–є –Њ–±–ї–∞—Б—В—Ц –≤–Є–Ј–љ–∞—З–µ–љ–љ—П
Ω ќ© -->
{\displaystyle \Omega }
Ω ќ© -->
{\displaystyle \Omega }
(
∂ вИВ -->
F
∂ вИВ -->
x
)
2
+
(
∂ вИВ -->
F
∂ вИВ -->
y
)
2
+
(
∂ вИВ -->
F
∂ вИВ -->
z
)
2
>
0
{\displaystyle \left({\frac {\partial F}{\partial x}}\right)^{2}+\left({\frac {\partial F}{\partial y}}\right)^{2}+\left({\frac {\partial F}{\partial z}}\right)^{2}>0}
–Т–Є–њ–∞–і–Њ–Ї –њ–∞—А–∞–Љ–µ—В—А–Є—З–љ–Њ–≥–Њ –Ј–∞–і–∞–љ–љ—П. –Ч–∞–і–∞–Љ–Њ –њ–Њ–≤–µ—А—Е–љ—О –≤–µ–Ї—В–Њ—А–љ–Є–Љ —А—Ц–≤–љ—П–љ–љ—П–Љ
r
=
r
(
u
,
v
)
{\displaystyle \mathbf {r} =\mathbf {r} (u,\ v)}
{
x
=
x
(
u
,
v
)
y
=
y
(
u
,
v
)
z
=
z
(
u
,
v
)
(
u
,
v
)
∈ вИИ -->
Ω ќ© -->
{\displaystyle \left\{{\begin{array}{ccc}x&=&x(u,v)\\y&=&y(u,v)\\z&=&z(u,v)\end{array}}\right.\quad (u,\,v)\in \Omega }
–¶—П —Б–Є—Б—В–µ–Љ–∞ —А—Ц–≤–љ—П–љ—М –Ј–∞–і–∞—Ф –≥–ї–∞–і–Ї—Г —А–µ–≥—Г–ї—П—А–љ—Г –њ–Њ–≤–µ—А—Е–љ—О , —П–Ї—Й–Њ:
—Б–Є—Б—В–µ–Љ–∞ –≤—Б—В–∞–љ–Њ–≤–ї—О—Ф –≤–Ј–∞—Ф–Љ–љ–Њ –Њ–і–љ–Њ–Ј–љ–∞—З–љ—Г –≤—Ц–і–њ–Њ–≤—Ц–і–љ—Ц—Б—В—М –Љ—Ц–ґ –Њ–±—А–∞–Ј–Њ–Љ —В–∞ –њ—А–Њ–Њ–±—А–∞–Ј–Њ–Љ
Ω ќ© -->
{\displaystyle \Omega }
—Д—Г–љ–Ї—Ж—Ц—Ч
x
(
u
,
v
)
,
y
(
u
,
v
)
,
z
(
u
,
v
)
{\displaystyle x(u,v),\,y(u,v),\,z(u,v)}
Ω ќ© -->
{\displaystyle \Omega }
–≤–Є–Ї–Њ–љ–∞–љ–∞ —Г–Љ–Њ–≤–∞ –љ–µ–≤–Є—А–Њ–і–ґ–µ–љ–Њ—Б—В—Ц:
|
x
u
′
x
v
′
y
u
′
y
v
′
|
2
+
|
y
u
′
y
v
′
z
u
′
z
v
′
|
2
+
|
z
u
′
z
v
′
x
u
′
x
v
′
|
2
>
0
{\displaystyle {\begin{vmatrix}x'_{u}&x'_{v}\\y'_{u}&y'_{v}\end{vmatrix}}^{2}+{\begin{vmatrix}y'_{u}&y'_{v}\\z'_{u}&z'_{v}\end{vmatrix}}^{2}+{\begin{vmatrix}z'_{u}&z'_{v}\\x'_{u}&x'_{v}\end{vmatrix}}^{2}>0}
–У–µ–Њ–Љ–µ—В—А–Є—З–љ–Њ –Њ—Б—В–∞–љ–љ—П —Г–Љ–Њ–≤–∞ –Њ–Ј–љ–∞—З–∞—Ф, —Й–Њ –≤–µ–Ї—В–Њ—А–Є
∂ вИВ -->
r
∂ вИВ -->
u
,
∂ вИВ -->
r
∂ вИВ -->
v
{\displaystyle {\frac {\partial \mathbf {r} }{\partial u}},{\frac {\partial \mathbf {r} }{\partial v}}}
–Ъ–Њ–Њ—А–і–Є–љ–∞—В–љ–∞ —Б—Ц—В–Ї–∞ –љ–∞ —Б—Д–µ—А—Ц –Я–∞—А–∞–Љ–µ—В—А–Є u, v –Љ–Њ–ґ–љ–∞ —А–Њ–Ј–≥–ї—П–і–∞—В–Є —П–Ї –≤–љ—Г—В—А—Ц—И–љ—Ц –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є —В–Њ—З–Њ–Ї –њ–Њ–≤–µ—А—Е–љ—Ц. –§—Ц–Ї—Б—Г—О—З–Є –Њ–і–љ—Г –Ј –Ї–Њ–Њ—А–і–Є–љ–∞—В, –Љ–Є –Њ—В—А–Є–Љ—Г—Ф–Љ–Њ –і–≤–∞ —Б—Ц–Љ–µ–є—Б—В–≤–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Є—Е –Ї—А–Є–≤–Є—Е , —Й–Њ –њ–Њ–Ї—А–Є–≤–∞—О—В—М –њ–Њ–≤–µ—А—Е–љ—О –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–Њ—О —Б—Ц—В–Ї–Њ—О.
–Т–Є–њ–∞–і–Њ–Ї —П–≤–љ–Њ–≥–Њ –Ј–∞–і–∞–љ–љ—П. –Я–Њ–≤–µ—А—Е–љ—П
S
{\displaystyle S}
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
S
{\displaystyle S}
–≥–ї–∞–і–Ї–Њ—О —А–µ–≥—Г–ї—П—А–љ–Њ—О –њ–Њ–≤–µ—А—Е–љ–µ—О , —П–Ї—Й–Њ —Д—Г–љ–Ї—Ж—Ц—П
f
{\displaystyle f}
x
=
u
;
y
=
v
;
z
=
f
(
u
,
v
)
{\displaystyle x=u;\ y=v;\ z=f(u,v)}
–Ф–Њ—В–Є—З–љ–∞ –њ–ї–Њ—Й–Є–љ–∞ –≤ —В–Њ—З—Ж—Ц –њ–Њ–≤–µ—А—Е–љ—Ц. –Ф–Њ—В–Є—З–љ–∞ –њ–ї–Њ—Й–Є–љ–∞ –≤ —В–Њ—З—Ж—Ц –≥–ї–∞–і–Ї–Њ—Ч –њ–Њ–≤–µ—А—Е–љ—Ц вАФ —Ж–µ –њ–ї–Њ—Й–Є–љ–∞, —Й–Њ –Љ–∞—Ф –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Є–є –њ–Њ—А—П–і–Њ–Ї –і–Њ—В–Є–Ї—Г –Ј –њ–Њ–≤–µ—А—Е–љ–µ—О –≤ —Ж—Ц–є —В–Њ—З—Ж—Ц. –Х–Ї–≤—Ц–≤–∞–ї–µ–љ—В–љ–Є–є –≤–∞—А—Ц–∞–љ—В –≤–Є–Ј–љ–∞—З–µ–љ–љ—П: –і–Њ—В–Є—З–љ–Њ—О –њ–ї–Њ—Й–Є–љ–Њ—О —Ф –њ–ї–Њ—Й–Є–љ–∞, —Й–Њ –Љ—Ц—Б—В–Є—В—М –і–Њ—В–Є—З–љ—Ц –і–Њ –≤—Б—Ц—Е –≥–ї–∞–і–Ї–Є—Е –Ї—А–Є–≤–Є—Е, —П–Ї—Ц –њ—А–Њ—Е–Њ–і—П—В—М —З–µ—А–µ–Ј —Ж—О —В–Њ—З–Ї—Г.
–Э–µ—Е–∞–є –≥–ї–∞–і–Ї–∞ –Ї—А–Є–≤–∞ –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—З–љ–Њ –Ј–∞–і–∞–љ—Ц–є –њ–Њ–≤–µ—А—Е–љ—Ц
r
=
r
(
u
,
v
)
{\displaystyle \mathbf {r} =\mathbf {r} (u,\ v)}
u
=
u
(
t
)
;
v
=
v
(
t
)
{\displaystyle u=u(t);\ v=v(t)}
–Э–∞–њ—А—П–Љ–Њ–Ї
v
{\displaystyle \mathbf {v} }
v
=
d
r
d
t
=
∂ вИВ -->
r
∂ вИВ -->
u
d
u
d
t
+
∂ вИВ -->
r
∂ вИВ -->
v
d
v
d
t
{\displaystyle \mathbf {v} ={\frac {d\mathbf {r} }{dt}}={\frac {\partial \mathbf {r} }{\partial u}}{\frac {du}{dt}}+{\frac {\partial \mathbf {r} }{\partial v}}{\frac {dv}{dt}}}
–Ч–≤—Ц–і—Б–Є –≤–Є–і–љ–Њ, —Й–Њ –≤—Б—Ц –і–Њ—В–Є—З–љ—Ц –і–Њ –≤—Б—Ц—Е –Ї—А–Є–≤–Є—Е —Г –і–∞–љ—Ц–є —В–Њ—З—Ж—Ц –ї–µ–ґ–∞—В—М –≤ –Њ–і–љ—Ц–є –њ–ї–Њ—Й–Є–љ—Ц, —Й–Њ –Љ—Ц—Б—В–Є—В—М –≤–µ–Ї—В–Њ—А–Є
∂ вИВ -->
r
∂ вИВ -->
u
,
∂ вИВ -->
r
∂ вИВ -->
v
{\displaystyle {\frac {\partial \mathbf {r} }{\partial u}},{\frac {\partial \mathbf {r} }{\partial v}}}
–†—Ц–≤–љ—П–љ–љ—П –і–Њ—В–Є—З–љ–Њ—Ч –њ–ї–Њ—Й–Є–љ–Є –≤ —В–Њ—З—Ж—Ц
r
0
=
(
x
0
,
y
0
,
z
0
)
{\displaystyle \mathbf {r_{0}} =(x_{0},y_{0},z_{0})}
(
r
− вИТ -->
r
0
,
∂ вИВ -->
r
∂ вИВ -->
u
,
∂ вИВ -->
r
∂ вИВ -->
v
)
=
0
{\displaystyle \left(\mathbf {r} -\mathbf {r_{0}} ,{\frac {\partial \mathbf {r} }{\partial u}},{\frac {\partial \mathbf {r} }{\partial v}}\right)=0\quad }
–Љ—Ц—И–∞–љ–Є–є –і–Њ–±—Г—В–Њ–Ї –≤–µ–Ї—В–Њ—А—Ц–≤).–£ –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е —А—Ц–≤–љ—П–љ–љ—П –і–Њ—В–Є—З–љ–Њ—Ч –њ–ї–Њ—Й–Є–љ–Є –і–ї—П —А—Ц–Ј–љ–Є—Е —Б–њ–Њ—Б–Њ–±—Ц–≤ –Ј–∞–і–∞–љ–љ—П –њ–Њ–≤–µ—А—Е–љ—Ц –љ–∞–≤–µ–і–µ–љ—Ц –≤ —В–∞–±–ї–Є—Ж—Ц:
–Ф–Њ—В–Є—З–љ–∞ –њ–ї–Њ—Й–Є–љ–∞ –і–Њ –њ–Њ–≤–µ—А—Е–љ—Ц –≤ —В–Њ—З—Ж—Ц
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
–Э–µ—П–≤–љ–µ –Ј–∞–і–∞–љ–љ—П
∂ вИВ -->
F
∂ вИВ -->
x
(
x
− вИТ -->
x
0
)
+
∂ вИВ -->
F
∂ вИВ -->
y
(
y
− вИТ -->
y
0
)
+
∂ вИВ -->
F
∂ вИВ -->
z
(
z
− вИТ -->
z
0
)
=
0
{\displaystyle {\frac {\partial F}{\partial x}}(x-x_{0})+{\frac {\partial F}{\partial y}}(y-y_{0})+{\frac {\partial F}{\partial z}}(z-z_{0})=0}
–ѓ–≤–љ–µ –Ј–∞–і–∞–љ–љ—П
∂ вИВ -->
f
∂ вИВ -->
x
(
x
− вИТ -->
x
0
)
+
∂ вИВ -->
f
∂ вИВ -->
y
(
y
− вИТ -->
y
0
)
=
(
z
− вИТ -->
z
0
)
{\displaystyle {\frac {\partial f}{\partial x}}(x-x_{0})+{\frac {\partial f}{\partial y}}(y-y_{0})=(z-z_{0})}
–Я–∞—А–∞–Љ–µ—В—А–Є—З–љ–µ –Ј–∞–і–∞–љ–љ—П
|
x
− вИТ -->
x
0
y
− вИТ -->
y
0
z
− вИТ -->
z
0
x
u
′
y
u
′
z
u
′
x
v
′
y
v
′
z
v
′
|
=
0
{\displaystyle {\begin{vmatrix}x-x_{0}&y-y_{0}&z-z_{0}\\x_{u}'&y_{u}'&z_{u}'\\x_{v}'&y_{v}'&z_{v}'\end{vmatrix}}=0}
–Т—Б—Ц –њ–Њ—Е—Ц–і–љ—Ц –Њ–±—З–Є—Б–ї—О—О—В—М—Б—П –≤ —В–Њ—З—Ж—Ц
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
–†–Њ–Ј–≥–ї—П–љ–µ–Љ–Њ –≥–ї–∞–і–Ї—Г –Ї—А–Є–≤—Г:
u
=
u
(
t
)
;
v
=
v
(
t
)
{\displaystyle u=u(t);\ v=v(t)}
–Х–ї–µ–Љ–µ–љ—В —Ч—Ч –і–Њ–≤–ґ–Є–љ–Є –≤–Є–Ј–љ–∞—З–∞—Ф—В—М—Б—П –Ј—Ц —Б–њ—Ц–≤–≤—Ц–і–љ–Њ—И–µ–љ–љ—П:
d
s
2
=
|
d
r
|
2
=
(
∂ вИВ -->
r
∂ вИВ -->
u
d
u
+
∂ вИВ -->
r
∂ вИВ -->
v
d
v
)
2
=
E
d
u
2
+
2
F
d
u
d
v
+
G
d
v
2
{\displaystyle ds^{2}=|d\mathbf {r} |^{2}=\left({\frac {\partial \mathbf {r} }{\partial u}}du+{\frac {\partial \mathbf {r} }{\partial v}}dv\right)^{2}=E\,du^{2}+2F\,du\,dv+G\,dv^{2}}
–і–µ
E
=
r
u
′
r
u
′
;
F
=
r
u
′
r
v
′
;
G
=
r
v
′
r
v
′
{\displaystyle E=\mathbf {r'_{u}} \mathbf {r'_{u}} ;\ F=\mathbf {r'_{u}} \mathbf {r'_{v}} ;\ G=\mathbf {r'_{v}} \mathbf {r'_{v}} }
–¶—П –Ї–≤–∞–і—А–∞—В–Є—З–љ–∞ —Д–Њ—А–Љ–∞ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –њ–µ—А—И–Њ—О –Ї–≤–∞–і—А–∞—В–Є—З–љ–Њ—О —Д–Њ—А–Љ–Њ—О –Љ–µ—В—А–Є–Ї–Є –њ–Њ–≤–µ—А—Е–љ—Ц. –Ф–ї—П —А–µ–≥—Г–ї—П—А–љ–Њ—Ч –њ–Њ–≤–µ—А—Е–љ—Ц —Ч—Ч –і–Є—Б–Ї—А–Є–Љ—Ц–љ–∞–љ—В
E
G
− вИТ -->
F
2
>
0
{\displaystyle EG-F^{2}>0}
F
=
0
{\displaystyle ~F=0}
–њ–ї–Њ—Й–Є–љ—Ц –Ј –і–µ–Ї–∞—А—В–Њ–≤–Є–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є
u
,
v
{\displaystyle u,v}
d
s
2
=
d
u
2
+
d
v
2
{\displaystyle ds^{2}=du^{2}+dv^{2}}
—В–µ–Њ—А–µ–Љ–∞ –Я—Ц—Д–∞–≥–Њ—А–∞ ).
–Я–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П –≥–µ–ї—Ц–Ї–Њ—Ч–і–∞ –≤ –Ї–∞—В–µ–љ–Њ—Ч–і . –Ь–µ—В—А–Є–Ї–∞ –љ–µ –≤–Є–Ј–љ–∞—З–∞—Ф –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ —Д–Њ—А–Љ—Г –њ–Њ–≤–µ—А—Е–љ—Ц. –Э–∞–њ—А–Є–Ї–ї–∞–і, –Љ–µ—В—А–Є–Ї–Є –≥–µ–ї—Ц–Ї–Њ—Ч–і–∞ —В–∞ –Ї–∞—В–µ–љ–Њ—Ч–і–∞ , –њ–∞—А–∞–Љ–µ—В—А–Є–Ј–Њ–≤–∞–љ–Є—Е –≤—Ц–і–њ–Њ–≤—Ц–і–љ–Є–Љ —З–Є–љ–Њ–Љ, –Ј–±—Ц–≥–∞—О—В—М—Б—П, —В–Њ–±—В–Њ –Љ—Ц–ґ —Ч—Е –Њ–±–ї–∞—Б—В—П–Љ–Є —Ц—Б–љ—Г—Ф –≤—Ц–і–њ–Њ–≤—Ц–і–љ—Ц—Б—В—М, —Й–Њ –Ј–±–µ—А—Ц–≥–∞—Ф –≤—Б—Ц –і–Њ–≤–ґ–Є–љ–Є (—Ц–Ј–Њ–Љ–µ—В—А—Ц—П ). –Т–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц, —Й–Њ –Ј–±–µ—А—Ц–≥–∞—О—В—М—Б—П –њ—А–Є —Ц–Ј–Њ–Љ–µ—В—А–Є—З–љ–Є—Е –њ–µ—А–µ—В–≤–Њ—А–µ–љ–љ—П—Е, –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П –≤–љ—Г—В—А—Ц—И–љ—М–Њ—О –≥–µ–Њ–Љ–µ—В—А—Ц—Ф—О –њ–Њ–≤–µ—А—Е–љ—Ц, –∞ —Б–∞–Љ—Ц –њ–Њ–≤–µ—А—Е–љ—Ц –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П —Ц–Ј–Њ–Љ–µ—В—А–Є—З–љ–Є–Љ–Є . –Т–љ—Г—В—А—Ц—И–љ—П –≥–µ–Њ–Љ–µ—В—А—Ц—П –љ–µ –Ј–∞–ї–µ–ґ–Є—В—М –≤—Ц–і –њ–Њ–ї–Њ–ґ–µ–љ–љ—П –њ–Њ–≤–µ—А—Е–љ—Ц –≤ –њ—А–Њ—Б—В–Њ—А—Ц —Ц –љ–µ –Ј–Љ—Ц–љ—О—Ф—В—М—Б—П –њ—А–Є —Ч—Ч –Ј–≥–Є–љ–∞–љ–љ—Ц –±–µ–Ј —А–Њ–Ј—В—П–≥—Г–≤–∞–љ–љ—П —В–∞ —Б—В–Є—Б–љ–µ–љ–љ—П (–љ–∞–њ—А–Є–Ї–ї–∞–і, –њ—А–Є –Ј–≥–Є–љ–∞–љ–љ—Ц —Ж–Є–ї—Ц–љ–і—А–∞ –≤ –Ї–Њ–љ—Г—Б ).
–Ь–µ—В—А–Є—З–љ—Ц –Ї–Њ–µ—Д—Ц—Ж—Ц—Ф–љ—В–Є
E
,
F
,
G
{\displaystyle E,\ F,\ G}
–Ї—А–Є–≤–Є–љ–Є —В–∞ —Ц–љ—И–µ. –Ґ–Њ–Љ—Г –≤—Б–µ, —Й–Њ –Ј–∞–ї–µ–ґ–Є—В—М –ї–Є—И–µ –≤—Ц–і –Љ–µ—В—А–Є–Ї–Є, –љ–∞–ї–µ–ґ–Є—В—М –і–Њ –≤–љ—Г—В—А—Ц—И–љ—М–Њ—Ч –≥–µ–Њ–Љ–µ—В—А—Ц—Ч.
–Т–µ–Ї—В–Њ—А–Є –љ–Њ—А–Љ–∞–ї—Ц –≤ —В–Њ—З–Ї–∞—Е –њ–Њ–≤–µ—А—Е–љ—Ц –Ю–і–љ—Ц—Ф—О –Ј –Њ—Б–љ–Њ–≤–љ–Є—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї –њ–Њ–≤–µ—А—Е–љ—Ц —Ф —Ч—Ч –љ–Њ—А–Љ–∞–ї—М
m
=
[
r
u
′
,
r
v
′
]
|
[
r
u
′
,
r
v
′
]
|
{\displaystyle \mathbf {m} ={\frac {[\mathbf {r'_{u}} ,\mathbf {r'_{v}} ]}{|[\mathbf {r'_{u}} ,\mathbf {r'_{v}} ]|}}}
–Ч–љ–∞–Ї –љ–Њ—А–Љ–∞–ї—Ц –Ј–∞–ї–µ–ґ–Є—В—М –≤—Ц–і –≤–Є–±–Њ—А—Г –Ї–Њ–Њ—А–і–Є–љ–∞—В.
–Я–µ—А–µ—В–Є–љ –њ–Њ–≤–µ—А—Е–љ—Ц –њ–ї–Њ—Й–Є–љ–Њ—О, —Й–Њ –Љ—Ц—Б—В–Є—В—М –љ–Њ—А–Љ–∞–ї—М (—Г –і–∞–љ—Ц–є —В–Њ—З—Ж—Ц), —Г—В–≤–Њ—А—О—Ф –љ–∞ –њ–Њ–≤–µ—А—Е–љ—Ц –і–µ—П–Ї—Г –Ї—А–Є–≤—Г, —П–Ї–∞ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –љ–Њ—А–Љ–∞–ї—М–љ–Є–Љ –њ–µ—А–µ—В–Є–љ–Њ–Љ –њ–Њ–≤–µ—А—Е–љ—Ц. –У–Њ–ї–Њ–≤–љ–∞ –љ–Њ—А–Љ–∞–ї—М –і–ї—П –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–µ—А–µ—В–Є–љ—Г –Ј–±—Ц–≥–∞—Ф—В—М—Б—П –Ј –љ–Њ—А–Љ–∞–ї–ї—О –і–Њ –њ–Њ–≤–µ—А—Е–љ—Ц (–Ј —В–Њ—З–љ—Ц—Б—В—О –і–Њ –Ј–љ–∞–Ї—Г).
–ѓ–Ї—Й–Њ –ґ –Ї—А–Є–≤–∞ –љ–∞ –њ–Њ–≤–µ—А—Е–љ—Ц –љ–µ —Ф –љ–Њ—А–Љ–∞–ї—М–љ–Є–Љ –њ–µ—А–µ—В–Є–љ–Њ–Љ, —В–Њ —Ч—Ч –≥–Њ–ї–Њ–≤–љ–∞ –љ–Њ—А–Љ–∞–ї—М —Г—В–≤–Њ—А—О—Ф –Ј –љ–Њ—А–Љ–∞–ї–ї—О –њ–Њ–≤–µ—А—Е–љ—Ц –і–µ—П–Ї–Є–є –Ї—Г—В
θ ќЄ -->
{\displaystyle \theta }
k
{\displaystyle k}
k
n
{\displaystyle k_{n}}
—Д–Њ—А–Љ—Г–ї–Њ—О –Ь–µ–љ—М—Ф :
k
n
=
± ¬± -->
k
cos
θ ќЄ -->
{\displaystyle k_{n}=\pm k\,\cos \,\theta }
–Ъ–Њ–Њ—А–і–Є–љ–∞—В–Є –Њ—А—В–∞ –љ–Њ—А–Љ–∞–ї—Ц –і–ї—П —А—Ц–Ј–љ–Є—Е —Б–њ–Њ—Б–Њ–±—Ц–≤ –Ј–∞–і–∞–љ–љ—П –њ–Њ–≤–µ—А—Е–љ—Ц –љ–∞–≤–µ–і–µ–љ—Ц –≤ —В–∞–±–ї–Є—Ж—Ц:
–Ъ–Њ–Њ—А–і–Є–љ–∞—В–Є –љ–Њ—А–Љ–∞–ї—Ц –≤ —В–Њ—З—Ж—Ц –њ–Њ–≤–µ—А—Е–љ—Ц
–Э–µ—П–≤–љ–µ –Ј–∞–і–∞–љ–љ—П
(
∂ вИВ -->
F
∂ вИВ -->
x
;
∂ вИВ -->
F
∂ вИВ -->
y
;
∂ вИВ -->
F
∂ вИВ -->
z
)
(
∂ вИВ -->
F
∂ вИВ -->
x
)
2
+
(
∂ вИВ -->
F
∂ вИВ -->
y
)
2
+
(
∂ вИВ -->
F
∂ вИВ -->
z
)
2
{\displaystyle {\frac {\left({\frac {\partial F}{\partial x}};\,{\frac {\partial F}{\partial y}};\,{\frac {\partial F}{\partial z}}\right)}{\sqrt {\left({\frac {\partial F}{\partial x}}\right)^{2}+\left({\frac {\partial F}{\partial y}}\right)^{2}+\left({\frac {\partial F}{\partial z}}\right)^{2}}}}}
–ѓ–≤–љ–µ –Ј–∞–і–∞–љ–љ—П
(
− вИТ -->
∂ вИВ -->
f
∂ вИВ -->
x
;
− вИТ -->
∂ вИВ -->
f
∂ вИВ -->
y
;
1
)
(
∂ вИВ -->
f
∂ вИВ -->
x
)
2
+
(
∂ вИВ -->
f
∂ вИВ -->
y
)
2
+
1
{\displaystyle {\frac {\left(-{\frac {\partial f}{\partial x}};\,-{\frac {\partial f}{\partial y}};\,1\right)}{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}}}
–Я–∞—А–∞–Љ–µ—В—А–Є—З–љ–µ –Ј–∞–і–∞–љ–љ—П
(
D
(
y
,
z
)
D
(
u
,
v
)
;
D
(
z
,
x
)
D
(
u
,
v
)
;
D
(
x
,
y
)
D
(
u
,
v
)
)
(
D
(
y
,
z
)
D
(
u
,
v
)
)
2
+
(
D
(
z
,
x
)
D
(
u
,
v
)
)
2
+
(
D
(
x
,
y
)
D
(
u
,
v
)
)
2
{\displaystyle {\frac {\left({\frac {D(y,z)}{D(u,v)}};\,{\frac {D(z,x)}{D(u,v)}};\,{\frac {D(x,y)}{D(u,v)}}\right)}{\sqrt {\left({\frac {D(y,z)}{D(u,v)}}\right)^{2}+\left({\frac {D(z,x)}{D(u,v)}}\right)^{2}+\left({\frac {D(x,y)}{D(u,v)}}\right)^{2}}}}}
–Ґ—Г—В:
D
(
y
,
z
)
D
(
u
,
v
)
=
|
y
u
′
y
v
′
z
u
′
z
v
′
|
,
D
(
z
,
x
)
D
(
u
,
v
)
=
|
z
u
′
z
v
′
x
u
′
x
v
′
|
,
D
(
x
,
y
)
D
(
u
,
v
)
=
|
x
u
′
x
v
′
y
u
′
y
v
′
|
{\displaystyle {\frac {D(y,z)}{D(u,v)}}={\begin{vmatrix}y'_{u}&y'_{v}\\z'_{u}&z'_{v}\end{vmatrix}},\quad {\frac {D(z,x)}{D(u,v)}}={\begin{vmatrix}z'_{u}&z'_{v}\\x'_{u}&x'_{v}\end{vmatrix}},\quad {\frac {D(x,y)}{D(u,v)}}={\begin{vmatrix}x'_{u}&x'_{v}\\y'_{u}&y'_{v}\end{vmatrix}}}
–Т—Б—Ц –њ–Њ—Е—Ц–і–љ—Ц –±–µ—А—Г—В—М—Б—П –≤ —В–Њ—З—Ж—Ц
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
–Ф–ї—П —А—Ц–Ј–љ–Є—Е –љ–∞–њ—А—П–Љ–Ї—Ц–≤ —Г –Ј–∞–і–∞–љ—Ц–є —В–Њ—З—Ж—Ц –њ–Њ–≤–µ—А—Е–љ—Ц –≤–Є—Е–Њ–і–Є—В—М —А—Ц–Ј–љ–∞ –Ї—А–Є–≤–Є–љ–∞ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –њ–µ—А–µ—В–Є–љ—Г, —П–Ї–∞ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –љ–Њ—А–Љ–∞–ї—М–љ–Њ—О –Ї—А–Є–≤–Є–љ–Њ—О ; —Ч–є –њ—А–Є–њ–Є—Б—Г—Ф—В—М—Б—П –Ј–љ–∞–Ї –њ–ї—О—Б, —П–Ї—Й–Њ –≥–Њ–ї–Њ–≤–љ–∞ –љ–Њ—А–Љ–∞–ї—М –Ї—А–Є–≤–Њ—Ч –є–і–µ –≤ —В–Њ–Љ—Г –ґ –љ–∞–њ—А—П–Љ–Ї—Г, —Й–Њ —Ц –љ–Њ—А–Љ–∞–ї—М –і–Њ –њ–Њ–≤–µ—А—Е–љ—Ц, –∞–±–Њ –Љ—Ц–љ—Г—Б, —П–Ї—Й–Њ –љ–∞–њ—А—П–Љ–Ї–Є –љ–Њ—А–Љ–∞–ї–µ–є –њ—А–Њ—В–Є–ї–µ–ґ–љ—Ц.
–Т–Ј–∞–≥–∞–ї—Ц –Ї–∞–ґ—Г—З–Є, –≤ –Ї–Њ–ґ–љ—Ц–є —В–Њ—З—Ж—Ц –њ–Њ–≤–µ—А—Е–љ—Ц —Ц—Б–љ—Г—О—В—М –і–≤–∞ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є—Е –љ–∞–њ—А—П–Љ–Є
e
1
{\displaystyle e_{1}}
e
2
{\displaystyle e_{2}}
–≥–Њ–ї–Њ–≤–љ–Є–Љ–Є . –Т–Є–љ—П—В–Њ–Ї —Б—В–∞–љ–Њ–≤–Є—В—М –≤–Є–њ–∞–і–Њ–Ї, –Ї–Њ–ї–Є –љ–Њ—А–Љ–∞–ї—М–љ–∞ –Ї—А–Є–≤–Є–љ–∞ –≤ —Г—Б—Ц—Е –љ–∞–њ—А—П–Љ–Ї–∞—Е –Њ–і–љ–∞–Ї–Њ–≤–∞ (–љ–∞–њ—А–Є–Ї–ї–∞–і, —Г —Б—Д–µ—А–Є –∞–±–Њ –љ–∞ —В–Њ—А—Ж—Ц –µ–ї—Ц–њ—Б–Њ—Ч–і–∞ –Њ–±–µ—А—В–∞–љ–љ—П), —В–Њ–і—Ц –≤—Б—Ц –љ–∞–њ—А—П–Љ–Ї–Є –≤ —В–Њ—З—Ж—Ц вАФ –≥–Њ–ї–Њ–≤–љ—Ц.
–Я–Њ–≤–µ—А—Е–љ—Ц –Ј –≤—Ц–і'—Ф–Љ–љ–Њ—О (–ї—Ц–≤–Њ—А—Г—З), –љ—Г–ї—М–Њ–≤–Њ—О (–≤ —Ж–µ–љ—В—А—Ц) —В–∞ –і–ї–Њ–і–∞—В–љ–Њ—О (–њ—А–∞–≤–Њ—А—Г—З) –Ї—А–Є–≤–Є–љ–Њ—О. –Э–Њ—А–Љ–∞–ї—М–љ—Ц –Ї—А–Є–≤–Є–љ–Є –≤ –≥–Њ–ї–Њ–≤–љ–Є—Е –љ–∞–њ—А—П–Љ–Ї–∞—Е –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П –≥–Њ–ї–Њ–≤–љ–Є–Љ–Є –Ї—А–Є–≤–Є–љ–∞–Љ–Є ; –њ–Њ–Ј–љ–∞—З–Є–Љ–Њ —Ч—Е
κ ќЇ -->
1
{\displaystyle \kappa _{1}}
κ ќЇ -->
2
{\displaystyle \kappa _{2}}
K
=
κ ќЇ -->
1
κ ќЇ -->
2
{\displaystyle K=\kappa _{1}\kappa _{2}}
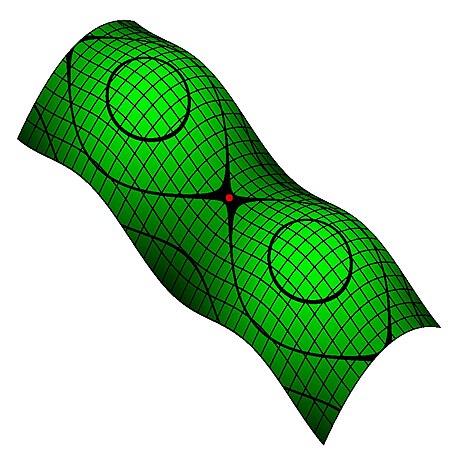
–љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –≥–∞—Г—Б–Њ–≤–Њ—О –Ї—А–Є–≤–Є–љ–Њ—О , –њ–Њ–≤–љ–Њ—О –Ї—А–Є–≤–Є–љ–Њ—О –∞–±–Њ –њ—А–Њ—Б—В–Њ –Ї—А–Є–≤–Є–љ–Њ—О –њ–Њ–≤–µ—А—Е–љ—Ц. –Ч—Г—Б—В—А—Ц—З–∞—Ф—В—М—Б—П —В–∞–Ї–Њ–ґ —В–µ—А–Љ—Ц–љ —Б–Ї–∞–ї—П—А –Ї—А–Є–≤–Є–љ–Є , —П–Ї–Є–є –Љ–∞—Ф –љ–∞ —Г–≤–∞–Ј—Ц —А–µ–Ј—Г–ї—М—В–∞—В –Ј–≥–Њ—А—В–Ї–Є —В–µ–љ–Ј–Њ—А–∞ –Ї—А–Є–≤–Є–љ–Є ; –њ—А–Є —Ж—М–Њ–Љ—Г —Б–Ї–∞–ї—П—А –Ї—А–Є–≤–Є–љ–Є –≤–і–≤—Ц—З—Ц –±—Ц–ї—М—И–Є–є, –љ—Ц–ґ –≥–∞—Г—Б–Њ–≤–∞ –Ї—А–Є–≤–Є–љ–∞.
–У–∞—Г—Б–Њ–≤–∞ –Ї—А–Є–≤–Є–љ–∞ –Љ–Њ–ґ–µ –±—Г—В–Є –Њ–±—З–Є—Б–ї–µ–љ–∞ —З–µ—А–µ–Ј –Љ–µ—В—А–Є–Ї—Г, —Ц —В–Њ–Љ—Г –≤–Њ–љ–∞ —Ф –Њ–±'—Ф–Ї—В–Њ–Љ –≤–љ—Г—В—А—Ц—И–љ—М–Њ—Ч –≥–µ–Њ–Љ–µ—В—А—Ц—Ч –њ–Њ–≤–µ—А—Е–Њ–љ—М (–≤—Ц–і–Ј–љ–∞—З–Є–Љ–Њ, —Й–Њ –≥–Њ–ї–Њ–≤–љ—Ц –Ї—А–Є–≤–Є–љ–Є –і–Њ –≤–љ—Г—В—А—Ц—И–љ—М–Њ—Ч –≥–µ–Њ–Љ–µ—В—А—Ц—Ч –љ–µ –љ–∞–ї–µ–ґ–∞—В—М). –Ч–∞ –Ј–љ–∞–Ї–Њ–Љ –Ї—А–Є–≤–Є–љ–Є –Љ–Њ–ґ–љ–∞ –Ї–ї–∞—Б–Є—Д—Ц–Ї—Г–≤–∞—В–Є —В–Њ—З–Ї–Є –њ–Њ–≤–µ—А—Е–љ—Ц (–і–Є–≤. –Љ–∞–ї—О–љ–Њ–Ї). –Ъ—А–Є–≤–Є–љ–∞ –њ–ї–Њ—Й–Є–љ–Є –і–Њ—А—Ц–≤–љ—О—Ф –љ—Г–ї—О. –Ъ—А–Є–≤–Є–љ–∞ —Б—Д–µ—А–Є —А–∞–і—Ц—Г—Б–∞ R –≤—Б—О–і–Є –і–Њ—А—Ц–≤–љ—О—Ф
1
R
2
{\displaystyle {\frac {1}{R^{2}}}}
–њ—Б–µ–≤–і–Њ—Б—Д–µ—А–∞ .
–Ъ—А–Є–≤–∞ –љ–∞ –њ–Њ–≤–µ—А—Е–љ—Ц –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –≥–µ–Њ–і–µ–Ј–Є—З–љ–Њ—О –ї—Ц–љ—Ц—Ф—О , –∞–±–Њ –њ—А–Њ—Б—В–Њ –≥–µ–Њ–і–µ–Ј–Є—З–љ–Њ—О , —П–Ї—Й–Њ —Г –≤—Б—Ц—Е —Ч—Ч —В–Њ—З–Ї–∞—Е –≥–Њ–ї–Њ–≤–љ–∞ –љ–Њ—А–Љ–∞–ї—М –і–Њ –Ї—А–Є–≤–Њ—Ч –Ј–±—Ц–≥–∞—Ф—В—М—Б—П –Ј –љ–Њ—А–Љ–∞–ї–ї—О –і–Њ –њ–Њ–≤–µ—А—Е–љ—Ц. –Я—А–Є–Ї–ї–∞–і: –љ–∞ –њ–ї–Њ—Й–Є–љ—Ц –≥–µ–Њ–і–µ–Ј–Є—З–љ–Є–Љ–Є –±—Г–і—Г—В—М –њ—А—П–Љ—Ц —В–∞ –≤—Ц–і—А—Ц–Ј–Ї–Є –њ—А—П–Љ–Є—Е, –љ–∞ —Б—Д–µ—А—Ц вАФ –≤–µ–ї–Є–Ї—Ц –Ї–Њ–ї–∞ —В–∞ —Ч—Е –≤—Ц–і—А—Ц–Ј–Ї–Є.
–Х–Ї–≤—Ц–≤–∞–ї–µ–љ—В–љ–∞ –≤–Є–Ј–љ–∞—З–µ–љ–љ—П: —Г –≥–µ–Њ–і–µ–Ј–Є—З–љ–Њ—Ч –ї—Ц–љ—Ц—Ч –њ—А–Њ—Ф–Ї—Ж—Ц—П —Ч—Ч –≥–Њ–ї–Њ–≤–љ–Њ—Ч –љ–Њ—А–Љ–∞–ї—Ц –љ–∞ –і–Њ—В–Є—З–љ—Г –њ–ї–Њ—Й–Є–љ—Г —Ф –љ—Г–ї—М–Њ–≤–Є–Љ –≤–µ–Ї—В–Њ—А–Њ–Љ. –ѓ–Ї—Й–Њ –Ї—А–Є–≤–∞ –љ–µ —Ф –≥–µ–Њ–і–µ–Ј–Є—З–љ–Њ—О, —В–Њ –Ј–∞–Ј–љ–∞—З–µ–љ–∞ –њ—А–Њ—Ф–Ї—Ж—Ц—П –љ–µ–љ—Г–ї—М–Њ–≤–∞; —Ч—Ч –і–Њ–≤–ґ–Є–љ–∞ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –≥–µ–Њ–і–µ–Ј–Є—З–љ–Њ—О –Ї—А–Є–≤–Є–љ–Њ—О
k
g
{\displaystyle k_{g}}
k
2
=
k
g
2
+
k
n
2
{\displaystyle k^{2}=k_{g}^{2}+k_{n}^{2}}
–і–µ
k
{\displaystyle k}
k
n
{\displaystyle k_{n}}
–У–µ–Њ–і–µ–Ј–Є—З–љ—Ц –ї—Ц–љ—Ц—Ч —Ф –Њ–±'—Ф–Ї—В–Њ–Љ –≤–љ—Г—В—А—Ц—И–љ—М–Њ—Ч –≥–µ–Њ–Љ–µ—В—А—Ц—Ч. –Я–µ—А–µ–ї—Ц—З–Є–Љ–Њ —Ч—Е –≥–Њ–ї–Њ–≤–љ—Ц –≤–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц:
–І–µ—А–µ–Ј –і–∞–љ—Г —В–Њ—З–Ї—Г –њ–Њ–≤–µ—А—Е–љ—Ц –≤ –Ј–∞–і–∞–љ–Њ–Љ—Г –љ–∞–њ—А—П–Љ–Ї—Г –њ—А–Њ—Е–Њ–і–Є—В—М –Њ–і–љ–∞ —Ц –ї–Є—И–µ –Њ–і–љ–∞ –≥–µ–Њ–і–µ–Ј–Є—З–љ–∞.
–Э–∞ –і–Њ—Б—В–∞—В–љ—М–Њ –Љ–∞–ї—Ц–є –і—Ц–ї—П–љ—Ж—Ц –њ–Њ–≤–µ—А—Е–љ—Ц –і–≤—Ц —В–Њ—З–Ї–Є –Ј–∞–≤–ґ–і–Є –Љ–Њ–ґ–љ–∞ –Ј'—Ф–і–љ–∞—В–Є –≥–µ–Њ–і–µ–Ј–Є—З–љ–Њ—О, —Ц –њ—А–Є—В–Њ–Љ—Г –ї–Є—И–µ –Њ–і–љ—Ц—Ф—О. –Я–Њ—П—Б–љ–µ–љ–љ—П: –љ–∞ —Б—Д–µ—А—Ц –њ—А–Њ—В–Є–ї–µ–ґ–љ—Ц –њ–Њ–ї—О—Б–Є –Ј'—Ф–і–љ—Г—Ф –љ–µ—Б–Ї—Ц–љ—З–µ–љ–љ–∞ –Ї—Ц–ї—М–Ї—Ц—Б—В—М –Љ–µ—А–Є–і—Ц–∞–љ—Ц–≤, –∞ –і–≤—Ц –±–ї–Є–Ј—М–Ї—Ц —В–Њ—З–Ї–Є –Љ–Њ–ґ–љ–∞ –Ј'—Ф–і–љ–∞—В–Є –љ–µ –ї–Є—И–µ –≤—Ц–і—А—Ц–Ј–Ї–Њ–Љ –≤–µ–ї–Є–Ї–Њ–≥–Њ –Ї–Њ–ї–∞, –∞–ї–µ —Ц –є–Њ–≥–Њ –і–Њ–њ–Њ–≤–љ–µ–љ–љ—П–Љ –і–Њ –њ–Њ–≤–љ–Њ–≥–Њ –Ї–Њ–ї–∞, —В–∞–Ї —Й–Њ –Њ–і–љ–Њ–Ј–љ–∞—З–љ—Ц—Б—В—М –≤–Є–Ї–Њ–љ—Г—Ф—В—М—Б—П –ї–Є—И–µ –≤ –Љ–∞–ї–Њ–Љ—Г –≤—Ц–і—А—Ц–Ј–Ї—Г.
–У–µ–Њ–і–µ–Ј–Є—З–љ–∞ —Ф –љ–∞–є–Ї–Њ—А–Њ—В—И–Њ—О. –С—Ц–ї—М—И —Б—В—А–Њ–≥–Њ: –љ–∞ –і–Њ—Б—В–∞—В–љ—М–Њ –Љ–∞–ї–Њ–Љ—Г –Њ–Ї–Њ–ї—Ц –њ–Њ–≤–µ—А—Е–љ—Ц –љ–∞–є–Ї–Њ—А–Њ—В—И–Є–є —И–ї—П—Е –Љ—Ц–ґ –Ј–∞–і–∞–љ–Є–Љ–Є —В–Њ—З–Ї–∞–Љ–Є –ї–µ–ґ–Є—В—М –љ–∞ –≥–µ–Њ–і–µ–Ј–Є—З–љ—Ц–є.
–©–µ –Њ–і–Є–љ –≤–∞–ґ–ї–Є–≤–Є–є –∞—В—А–Є–±—Г—В –њ–Њ–≤–µ—А—Е–љ—Ц вАФ —Ч—Ч –њ–ї–Њ—Й–∞
S
=
∬ вИђ -->
|
[
r
u
′
× √Ч -->
r
v
′
]
|
d
u
d
v
{\displaystyle S=\iint \,|[\mathbf {r} '_{u}\times \mathbf {r} '_{v}]|\;\mathrm {d} \,u\,\mathrm {d} \,v}
–Ґ—Г—В
r
u
′
=
{
∂ вИВ -->
x
∂ вИВ -->
u
,
∂ вИВ -->
y
∂ вИВ -->
u
,
∂ вИВ -->
z
∂ вИВ -->
u
}
,
r
v
′
=
{
∂ вИВ -->
x
∂ вИВ -->
v
,
∂ вИВ -->
y
∂ вИВ -->
v
,
∂ вИВ -->
z
∂ вИВ -->
v
}
{\displaystyle \mathbf {r} '_{u}=\left\{{\frac {\partial x}{\partial u}},\,{\frac {\partial y}{\partial u}},\,{\frac {\partial z}{\partial u}}\right\},\ \mathbf {r} '_{v}=\left\{{\frac {\partial x}{\partial v}},\,{\frac {\partial y}{\partial v}},\,{\frac {\partial z}{\partial v}}\right\}}
–Т –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Њ—В—А–Є–Љ—Г—Ф–Љ–Њ:
–ѓ–≤–љ–µ –Ј–∞–і–∞–љ–љ—П
–Я–∞—А–∞–Љ–µ—В—А–Є—З–љ–µ –Ј–∞–і–∞–љ–љ—П
–Т–Є—А–∞–Ј –і–ї—П –њ–ї–Њ—Й—Ц
∬ вИђ -->
(
∂ вИВ -->
f
∂ вИВ -->
x
)
2
+
(
∂ вИВ -->
f
∂ вИВ -->
y
)
2
+
1
d
x
d
y
{\displaystyle \iint \,{\sqrt {\left({\frac {\partial f}{\partial x}}\right)^{2}+\left({\frac {\partial f}{\partial y}}\right)^{2}+1}}\;\mathrm {d} \,x\,\mathrm {d} \,y}
∬ вИђ -->
(
D
(
x
,
y
)
D
(
u
,
v
)
)
2
+
(
D
(
y
,
z
)
D
(
u
,
v
)
)
2
+
(
D
(
z
,
x
)
D
(
u
,
v
)
)
2
d
u
d
v
{\displaystyle \iint \,{\sqrt {\left({\frac {D(x,y)}{D(u,v)}}\right)^{2}+\left({\frac {D(y,z)}{D(u,v)}}\right)^{2}+\left({\frac {D(z,x)}{D(u,v)}}\right)^{2}}}\;\mathrm {d} \,u\,\mathrm {d} \,v}
–°—В—А—Ц—З–Ї–∞ –Ь–µ–±—Ц—Г—Б–∞ –Ј—А–Њ–±–ї–µ–љ–∞ –Ј –Њ–і–љ–Њ–≥–Њ —И–Љ–∞—В–Ї–∞ –њ–∞–њ–µ—А—Г –∞–±–Њ —Б—В—А—Ц—З–Ї–Є. –Ґ–∞–Ї–Њ–ґ –≤–∞–ґ–ї–Є–≤–Њ—О —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Њ—О –њ–Њ–≤–µ—А—Е–љ—Ц —Ф —Ч—Ч –Њ—А—Ц—Ф–љ—В–∞—Ж—Ц—П .
–Я–Њ–≤–µ—А—Е–љ—П –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –і–≤–Њ—Б—В–Њ—А–Њ–љ–љ—М–Њ—О , —П–Ї—Й–Њ –≤–Њ–љ–∞ –љ–∞ –≤—Б—Ц–є —Ч—Ч –њ—А–Њ—В—П–ґ–љ–Њ—Б—В—Ц –Љ–∞—Ф –љ–µ–њ–µ—А–µ—А–≤–љ–µ –њ–Њ–Ї—А–Є—В—В—П –≤–µ–Ї—В–Њ—А–Њ–Љ –љ–Њ—А–Љ–∞–ї—Ц . –Т —Ц–љ—И–Њ–Љ—Г –≤–Є–њ–∞–і–Ї—Г –њ–Њ–≤–µ—А—Е–љ—О –љ–∞–Ј–Є–≤–∞—О—В—М –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ—М–Њ—О .
–Ю—А—Ц—Ф–љ—В–Њ–≤–∞–љ–Њ—О –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П –і–≤–Њ—Б—В–Њ—А–Њ–љ–љ—П –њ–Њ–≤–µ—А—Е–љ—П –Ј –≤–Є–±—А–∞–љ–Є–Љ –љ–∞–њ—А—П–Љ–Њ–Љ –љ–Њ—А–Љ–∞–ї—Ц.
–Я—А–Є–Ї–ї–∞–і–∞–Љ–Є –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ—Ц—Е –њ–Њ–≤–µ—А—Е–Њ–љ—М —Ф —Б—В—А—Ц—З–Ї–∞ –Ь–µ–±—Ц—Г—Б–∞ —В–∞ –њ–ї—П—И–Ї–∞ –Ъ–ї—П–є–љ–∞ .
–Ч —В–Њ—З–Ї–Є –Ј–Њ—А—Г —В–Њ–њ–Њ–ї–Њ–≥—Ц—З–љ–Њ—Ч –±—Г–і–Њ–≤–Є, –њ–Њ–≤–µ—А—Е–љ—Ц, —П–Ї –і–≤–Њ–≤–Є–Љ—Ц—А–љ—Ц –Љ–љ–Њ–≥–Њ–≤–Є–і–Є , –±—Г–≤–∞—О—В—М:





























































![{\displaystyle \mathbf {m} ={\frac {[\mathbf {r'_{u}} ,\mathbf {r'_{v}} ]}{|[\mathbf {r'_{u}} ,\mathbf {r'_{v}} ]|}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b48f171dc03043ba3872de68e9d5ad7de6dc3475)

















![{\displaystyle S=\iint \,|[\mathbf {r} '_{u}\times \mathbf {r} '_{v}]|\;\mathrm {d} \,u\,\mathrm {d} \,v}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e92d248abd3fd69edec9274f8ee10b590bcc547)




