Гиперсовершенное число
|
Read other articles:

Солкарум. Solca герб Основні дані 47°42′ пн. ш. 25°50′ сх. д. / 47.700° пн. ш. 25.833° сх. д. / 47.700; 25.833Координати: 47°42′ пн. ш. 25°50′ сх. д. / 47.700° пн. ш. 25.833° сх. д. / 47.700; 25.833 Країна РумуніяРегіон СучаваАдмінцентр Solca[d]Пл�...

1954 film by Franklin Adreon Trader Tom of the China SeasDirected byFranklin AdreonWritten byRonald DavidsonProduced byFranklin AdreonStarringHarry LauterAline TowneLyle TalbotRobert ShayneFred GrahamRichard ReevesJohn CrawfordGeorge SelkCinematographyBud ThackeryDistributed byRepublic PicturesRelease dates January 6, 1954 (1954-01-06) (U.S. serial)[1] 1966 (1966) (U.S. TV)[1] Running time12 chapters (167 minutes (serial)[1]100 minutes (TV)&...

Elliott Bay Luftbild der Elliott Bay Luftbild der Elliott Bay Gewässer Puget Sound Landmasse Nordamerika Geographische Lage 47° 36′ N, 122° 22′ W47.603-122.373Koordinaten: 47° 36′ N, 122° 22′ W Elliott Bay (Washington) Breite 10,5 km Tiefe 3,2 km Fläche 21 km² Zuflüsse Duwamish River Der Duwamish Head in West-Seattle Der Duwamish Head in West-Seattle Die Elliott Bay ist ein Teil der zentralen Region des Puget Sound im...
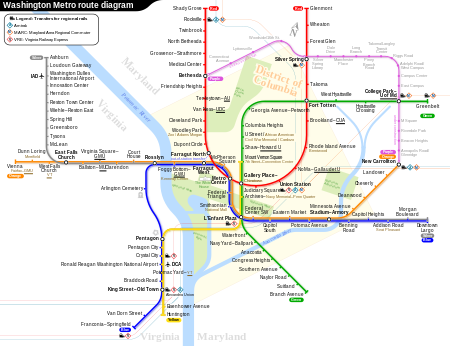
Rapid transit system serving the Washington metropolitan area Washington metro redirects here. For the metropolitan area of Washington, see Washington metropolitan area. Washington MetroWashington Metro's Farragut West station in April 2018OverviewLocaleWashington metropolitan areaTransit typeRapid transitNumber of lines6Line number Number of stations98Daily ridership415,900 (weekdays, Q2 2023)[1]Annual ridership93,049,300 (2022)[2]Chief executiveRandy ClarkeHeadquarters6...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Janeiro de 2020) Supergêmeos Arte de Alex Ross Informações gerais Primeira aparição Histórica: Super Amigos # 7 (Outubro de 1977)[1] Moderna: Justiça Extrema # 9 (outubro de 1995) Criado por E. Nelson Bridwell Editora DC Comics Info...

Gmina ZawojaNegara PolandiaProvinsiPolandia KecilPowiatSuchaIbudesaZawojaPemerintahan • Wali kotaMarcin PająkLuas • Total128,78 km2 (49,72 sq mi)Populasi (2006) • Total9,046 • Kepadatan70/km2 (180/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Postal code34-222Car platesKSUSitus webhttp://www.zawoja.pl/ Powiat Sucha (Gmina Zawoja) Gmina Zawoja (desa); 1 - Zawoja, 2 - Skawica Gmina Zawoja (ba...

National anthem of FranceFor other uses, see La Marseillaise (disambiguation). La MarseillaiseEnglish: The MarseillaiseThe Marseillais volunteers departing, sculpted on the Arc de TriompheNational anthem of FranceAlso known asChant de Guerre pour l'Armée du Rhin (English: War song for the Army of the Rhine)LyricsClaude Joseph Rouget de Lisle, 1792MusicClaude Joseph Rouget de LisleAdopted14 July 1795Readopted1870Relinquished1799Audio sampleLa Marseillaise (instrumental)filehelp La M...

Negara-negara bagian di FilipinaBagian dari seri artikel mengenaiSejarah Filipina Prasejarah (pra–900) Callao dan Tabon Kedatangan Suku Negrito Ekspansi Austronesia Petroglif Angono Periode klasik (900–1565) Ma-i Kerajaan Tondo Konfederasi Madya-as Kerajaan Manila Kerajaan Namayan Kerajaan Butuan Kerajaan Cebu Kesultanan Maguindanao Kesultanan Sulu Penjajahan Spanyol (1565–1898) Hindia Timur Spanyol Pengkristenan Konflik Spanyol–Moro Invasi Belanda Invasi Inggris Katipunan Revolusi Fi...

Academia de Polícia MilitarDom João VI Brasão País Brasil Estado Rio de Janeiro Corporação Polícia Militar do Estado do Rio de Janeiro Subordinação Diretoria Geral de Ensino e Instrução Sigla APM D. J. VI Criação 1920 Aniversários 1 de dezembro Patrono Dom João VI Marcha Canção da EsFO Lema Berço de líderes Sede Sede Rio de Janeiro Página oficial http://www.apmerj.com.br/ A Academia de Polícia Militar Dom João VI, antiga Escola de Formação de Oficiais - EsF...

この記事はドイツ語版の対応するページを翻訳することにより充実させることができます。(2020年11月)翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。 ドイツ語版記事を日本語へ機械翻訳したバージョン(Google翻訳)。 万が一翻訳の手がかりとして機械翻訳を用いた場合、翻訳者は必ず翻訳元原文を参照して機械翻訳の誤りを訂正し、正確な�...

Pemilihan umum Bupati Lampung Utara 20242018202927 November 2024Kandidat Peta persebaran suara Bupati & Wakil Bupati petahanaAgung Ilmu Mangkunegara & Budi Utomo Nasdem Bupati & Wakil Bupati terpilih belum diketahui Sunting kotak info • L • BBantuan penggunaan templat ini Pemilihan umum Bupati Lampung Utara 2024 dilaksanakan pada 27 November 2024 untuk memilih Bupati Lampung Utara periode 2024-2029.[1] Pemilihan Bupati (Pilbup) Lampung Utara tahun tersebut ak...

Este artículo o sección tiene referencias, pero necesita más para complementar su verificabilidad.Este aviso fue puesto el 17 de febrero de 2016. Gobierno Militar de Comodoro Rivadavia Territorio nacional 1944-1955 Ubicación de Zona Militar de Comodoro RivadaviaCapital Comodoro RivadaviaEntidad Territorio nacional • País ArgentinaIdioma oficial CastellanoPoblación hist. • 1951 est. 60 000 hab.Religión CatólicaHistoria • 31 de mayode 1944 De...

Ar-RawabiLingkunganNegara Arab SaudiProvinsiProvinsi MekkahKotaMekkahZona waktuUTC+3 (EAT) • Musim panas (DST)UTC+3 (EAT) Ar-Rawabi adalah sebuah lingkungan di kota suci Mekkah di Provinsi Mekkah, tepatnya di sebelah barat Arab Saudi. Referensi lbs MakkahSejarah Garis waktu Quraisy Kenabian Muhammad Muhammad di Makkah Penaklukan Makkah Rasyidin Umayyah Kekhalifahan Ibnu Zubair Pengepungan Makkah (683) Abbasiyah Mamluk Kairo Kesultanan Utsmaniyah Revolusi Arab Kerajaan Hijaz K...

Former municipality in Rogaland, Norway Former municipality in Rogaland, NorwayNærbø Municipality Nærbø herredFormer municipalityPanorama of Nærbø Rogaland within NorwayNærbø within RogalandCoordinates: 58°39′55″N 05°38′16″E / 58.66528°N 5.63778°E / 58.66528; 5.63778CountryNorwayCountyRogalandDistrictJærenEstablished1 Jan 1894 • Preceded byHaa MunicipalityDisestablished1 Jan 1964 • Succeeded byHå MunicipalityAdministrative&...

1988 murder in Cardiff This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Murder of Lynette White – news · newspapers · books · scholar · JSTOR (March 2022) (Learn how and when to remove this template message) Murder of Lynette WhiteLocation7 James Street, Butetown, Cardiff, WalesCoordinates51°27′54″N 3°0...

Rural district in East Azerbaijan province, Iran For other places with the same name, see Qeshlaq Rural District. For other places with a similar name, see Qeshlaq. Rural District in East Azerbaijan, IranQeshlaq Rural District Persian: دهستان قشلاقRural DistrictQeshlaq Rural DistrictCoordinates: 39°11′09″N 47°22′13″E / 39.18583°N 47.37028°E / 39.18583; 47.37028[1]Country IranProvinceEast AzerbaijanCountyKaleybarDistrictAbish AhmadCap...

Malaysian politician (1952–2021) In this Malay name, there is no family name. The name Kijo is a patronymic, and the person should be referred to by the given name, Ismail. Yang Berbahagia Dato' HajiIsmail KijoDPMS PPNإسماعيل کيجوMember of the Selangor State Legislative Assemblyfor Lembah JayaIn office24 April 1995 – 8 March 2008Preceded byConstituency createdSucceeded byKhasim Abdul Aziz (PAS) Personal detailsBorn(1952-05-28)28 May 1952Kampung Bukit Badong, Kua...

American actor For the politician, see Stephen Dunham (politician). Stephen DunhamBornStephen Dunham Bowers[1](1964-09-14)September 14, 1964Boston, Massachusetts, U.S.DiedSeptember 14, 2012(2012-09-14) (aged 48)Burbank, California, U.S.Other namesStephen BowersOccupationActorYears active1983–2012SpouseAlexondra Lee (2005–2012, his death) Stephen Dunham (September 14, 1964 – September 14, 2012) was an American actor, best known as Edward Pillows on the series DAG a...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Enakku Nane Needipathi – news · newspapers · books · scholar · JSTOR (June 2023) (Learn how and when to remove this template message) 1986 Indian filmEnakku Nane NeedipathiDirected byS. A. ChandrasekharScreenplay byS. A. ChandrasekharStory byShoba Chandrasekhar...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (June 2017) The Great CityGames is a major street athletics event[1] held twice annually in Manchester, Newcastle and Gateshead. The former is held in conjunction to the Great Manchester Run, a major 10k generally held on the Sunday. The first event was in May 2009.[2] The latter is held in conjunction to the Great North...



