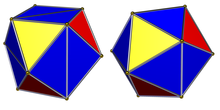
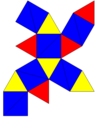
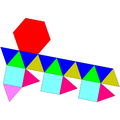
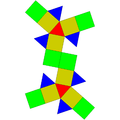
Icosahedron
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Ancient Cilician city For other uses, see Soli (disambiguation). Roman colonnade at the site.Soli (Ancient Greek: ќ£ѕМќїќњќє, S√≥loi), often rendered Soli/Pompeiopolis (Ancient Greek: ќ†ќњќЉѕАќЈѕКќњѕНѕАќњќїќєѕВ), was an ancient city and port in Cilicia, 11 km west of Mersin in present-day Turkey. Geography The red dot shows the position of Mersin in a map of present-day Turkey. At this scale, it coincides with the position of Soli. Pompeiopolis from an 1812 Admiralty Chart Located in Sou...

BudimanKepala Staf TNI Angkatan Darat ke-29Masa jabatan30 Agustus 2013 вАУ 25 Juli 2014PresidenSusilo Bambang YudhoyonoPanglima TNIAgus Suhartono (2013)Moeldoko (2013-14)PendahuluJenderal TNI MoeldokoPenggantiJenderal TNI Gatot NurmantyoPangdam IV/DiponegoroMasa jabatanOktober 2009 вАУ Juni 2010PendahuluMayjen TNI Haryadi SoetantoPenggantiMayor Jenderal TNI Langgeng Sulistiyono Informasi pribadiLahir25 September 1956 (umur 67)Jakarta, DKI JakartaKebangsaanIndonesiaP...

Derechos LGBT en SurinamBanderaEscudo Surinam en América del SurHomosexualidadEs legal Desde 1869Edad de consentimiento sexualHeterosexual y homosexual igual Edad de consentimiento homosexual 18 añosProtección legal contra la discriminaciónLaboral Bienes y servicios En todos los aspectos Protección legal de parejaAcceso igualitario a la unión civil Matrimonio entre personas del mismo sexo Derechos reproductivos y de adopciónAcceso igualitario a la adopción monoparental Derecho de adopci

Sei Putih Timur IKelurahanGapura selamat datang di Kelurahan Sei Putih Timur INegara IndonesiaProvinsiSumatera UtaraKotaMedanKecamatanMedan PetisahKodepos20118Kode Kemendagri12.71.19.1006 Kode BPS1275130005 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Sei Putih Timur I adalah kelurahan di kecamatan Medan Petisah, Medan, Sumatera Utara, Indonesia. Gereja HKBP Pabrik Tenun di Kelurahan Sei Putih Timur I lbsKecamatan Medan Petisah, Kota Medan, Sumatera UtaraKelurahan Petisah Te...

Dokter per 1.000 orang pada tahun 2018.[1] Dokter (bahasa Belanda: dokter, arts atau geneesheer; bahasa Inggris: medical doctor, disingkat M.D.; dari bahasa Latin medicinae doctor) adalah seseorang yang karena keilmuannya berusaha menyembuhkan orang-orang yang sakit. Tidak semua orang yang menyembuhkan penyakit bisa disebut dokter. Untuk menjadi dokter biasanya diperlukan pendidikan dan pelatihan khusus dan mempunyai gelar dalam bidang kedokteran. Etimologi Kata dokter diserap dari ba...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Bebe LillyNama lainBebe LillyAsalPerancisGenreMusik elektronikTahun aktif2006 - sekarangLabelHeben Music, Sony BMG Music Entertainment Indonesia Bébé Lilly adalah penyanyi animasi bayi perempuan di Perancis. Dia telah merilis 13 single, terutama dal...

Masjid Agung JamiaAgamaAfiliasi agamaSunni IslamDistrikLahoreProvinsiPunjabEcclesiastical or organizational statusMasjidKepemimpinanMalik RiazDiberkati2014LokasiLokasiBahria Town, Lahore, PakistanKoordinat31¬∞22вА≤5.16вА≥N 74¬∞11вА≤8.84вА≥E / 31.3681000¬∞N 74.1857889¬∞E / 31.3681000; 74.1857889Koordinat: 31¬∞22вА≤5.16вА≥N 74¬∞11вА≤8.84вА≥E / 31.3681000¬∞N 74.1857889¬∞E / 31.3681000; 74.1857889ArsitekturJenisMasjidGaya arsitekturIslami, MughalSpe...

Santa Helena Associa√І√£o Associa√І√£o de Futebol de Santa Helena Treinador Nick Stevens Capit√£o Rico Benjamin Mais participa√І√µes Rico Benjamin e Ronan Legg (5) Melhor marcador? Rico Benjamin (3) Uniformetitular Uniformealternativo Jogos 1.¬™ partida internacional N√£o-oficial: Lockheed Leamington 15вАУ3 Santa Helena (Leamington Spa, Inglaterra; 12 de novembro de 1949)Oficial: Anglesey 7вАУ2 Santa Helena (Bryn Du, Anglesey; 12 de junho de 2019) Melhor resultado Holyhead Hotspur 0вАУ2...

Ordem de Nossa Senhora da Caridade(O.D.N.C.) Ordem de Nossa Senhora da Caridade Ordem de Nossa Senhora da CaridadeO fundador, S√£o Jo√£o Eudes, com as religiosas da ordem. Tipo Ordem religiosa de clausura mon√°stica Funda√І√£o 25 de novembro de 1641 Fundador(a) S√£o Jo√£o Eudes S√≠tio oficial www.buonpastoreint.org O h√°bito religioso das Irm√£s da Ordem de Nossa Senhora da Caridade. A Ordem de Nossa Senhora da Caridade[1][2] (Latim: Ordo Dominae Nostrae de Caritate, sigla O.D.N.C.), tamb√©m ...

French actress Lilian ConstantiniLilian Constantini (Le P√®lerin)BornLiliane Louise H√©l√®ne Chapiro-VolpertSeptember 26, 1902Paris, FranceDiedJanuary 5, 1982 (1982-01-06) (aged 79)Saint-Tropez, FranceOccupationActressSpouseCharles SchneiderChildrenDominique SchneidreParent(s)Boris Chapiro-VolpertLouise GuesdeRelativesJules Guesde (maternal grandfather) Lilian Constantini (September 26, 1902 вАУ January 5, 1982) was a French silent actress in the 1920s and 1930s. Early life Liliane ...

Potret Zofia Albinowska-Minkiewiczow Zofia Albinowska-Minkiewiczowa (Klagenfurt, Kadipaten Kärnten, Austria-Hungaria 1886-1971, Lviv, Soviet Ukraina) adalah seorang seniman, pelukis dan pengukir Polandia dan Ukraina yang terikat pada lingkaran seniman Lviv, dan untuk bertahun-tahun presiden Persatuan Seniman Polandia (Zwiazek Artystów Polskich). Terlahir sebagai Zofia Albinowska, dia menandatangani lukisannya dengan cara ini. Dia kemudian menikah Witold Minkiewicz, profesor arsitektur di Lv...

Resolusi 827Dewan Keamanan PBBPengadilan Pidana Internasional untuk bekas YugoslaviaTanggal25 Mei 1993Sidang no.3.217KodeS/RES/827 (Dokumen)TopikPengadilan (Bekas Yugoslavia)Ringkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Brasil Tanjung Verde Djibouti Spanyol Hungaria Jepang Maroko S...

American-bred Thoroughbred racehorse For other uses, see Zenyatta (disambiguation). ZenyattaZenyatta winning the Lady's Secret StakesSireStreet CryGrandsireMachiavellianDamVertigineuxDamsireKris S.SexMareFoaled (2004-04-01) April 1, 2004 (age 19)Lexington, Kentucky, U.S.CountryUnited StatesColourDark Bay/BrownBreederMaverick Productions, LimitedOwnerJerry & Ann MossTrainerJohn ShirreffsJockeyMike SmithRecord20: 19вАУ1вАУ0Earnings$7,304,580[1]Major winsEl Encino Stakes (2008)A...

DulalowoKelurahanNegara IndonesiaProvinsiGorontaloKotaGorontaloKecamatanKota TengahKode Kemendagri75.71.06.1002 Kode BPS7571031002 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Kantor Lurah Dulalowo Dulalowo adalah salah satu kelurahan di wilayah kecamatan Kota Tengah, Kota Gorontalo, Provinsi Gorontalo, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, d...

1568 treaty which ended the second phase of the French Wars of Religion Treaty of LongjumeauPicture of Charles IX who issued the peaceSigned24 March 1568LocationLongjumeauSignatoriesCharles IX of France Louis, Prince of Conde (1530-1569)LanguagesFrench vteFrench Wars of Religion First; 1562вАУ1563Rouen; Vergt; Dreux; Orl√©ans Second; 1567вАУ1568Saint-Denis; Chartres Third; 1568вАУ1570Jarnac; La Roche-l'Abeille; Poitiers; Orthez; Moncontour; Saint-Jean d'Ang√©ly; Arney-le-Duc Fourth; 1572вАУ15...

1993 single by Things of Stone and WoodSingle Perfect RaindropCD single coverSingle by Things of Stone and Woodfrom the album The Yearning ReleasedJune 1993Length4:08LabelCapitolSongwriter(s)Greg ArnoldProducer(s)James Black, Martin PullanThings of Stone and Wood singles chronology Rock This Boat (1993) Single Perfect Raindrop (1993) Wildflowers (1994) Single Perfect Raindrop is a song written by Greg Arnold and recorded by Australian folk-rock band Things of Stone and Wood. The song was rele...

University in Hsinchu City, Taiwan This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (October 2014) (Learn how and when to remove this template message) Hsuan Chuang UniversityзОДе•Ше§Іе≠ЄMottoеЊЈжЩЇеЛ§жѓЕ(PeћНh-≈Нe-jƒЂ: Tek-t√ђ Kh√Ѓn-gƒУ)[1]Motto in EnglishVirtue, Knowledge, Diligence and Perseverance[2]TypePrivateEstablished1997Academi...

ж≠§жҐЭзЫЃйЬАи¶БжУіеЕЕгАВ (2014еєі7жЬИ6жЧ•)иѓЈеНФеК©жФєеЦДињЩзѓЗжҐЭзЫЃпЉМжЫійА≤дЄАж≠•зЪДдњ°жБѓеПѓиГљжЬГеЬ®и®ОиЂЦй†БжИЦжЙ©еЕЕиѓЈж±ВдЄ≠жЙЊеИ∞гАВиѓЈеЬ®жУіеЕЕжҐЭзЫЃеЊМе∞Зж≠§ж®°жЭњзІїйЩ§гАВ ж≠§жҐЭзЫЃйЬАи¶Би°•еЕЕжЫіе§ЪжЭ•жЇРгАВ (2014еєі7жЬИ6жЧ•)иѓЈеНПеК©и£ЬеЕЕе§ЪжЦєйЭҐеПѓйЭ†жЭ•жЇРдї•жФєеЦДињЩзѓЗжЭ°зЫЃпЉМжЧ†ж≥ХжЯ•иѓБзЪДеЖЕеЃєеПѓиГљжЬГеЫ†зВЇеЉВиЃЃжПРеЗЇиАМ襀粿йЩ§гАВиЗідљњзФ®иАЕпЉЪиѓЈжРЬ糥дЄАдЄЛжЭ°зЫЃзЪДж†ЗйҐШпЉИжЭ•жЇРжРЬ糥пЉЪиЕОдЄКиЕЇйЕЄ — зљСй°µгАБжЦ∞йЧїгАБдє¶з±НгАБе≠¶жЬѓгАБеЫЊеГПпЉЙпЉМдї•ж...

Library system in London, Ontario, Canada London Public LibraryLocationLondon, Ontario - Central Branch: 251 Dundas Street, CanadaEstablished1896Branches16CollectionItems collectedbusiness directories, phone books, maps, government publications, books, periodicals, genealogy, local historyAccess and useCirculation3,869,642 items borrowed 4,012,731 website visitsPopulation served2,737,988 annual visitsOther informationBudget$20,117,983DirectorMichael Ciccone (CEO & Chief Librarian)[1&#...

2013 video gameNarcoGuerraDeveloper(s)GameTheNewsEngineUnityPlatform(s)Windows, macOS, Android, iOSReleaseJune 2013Genre(s)Strategy, newsgameMode(s)Single-player NarcoGuerra, Spanish for DrugWar, is a strategy newsgame developed by GameTheNews.net. It was released in June 2013 for Android, PC, Mac, iPhone, iPod Touch and iPad. The game criticises the ongoing War on Drugs and more specifically the Mexican Drug War which the developer claims вА≥...is a challenging and tactical newsgame that put...