Zeno of Elea
| |||||||||||||||||||||
Read other articles:

Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak men...
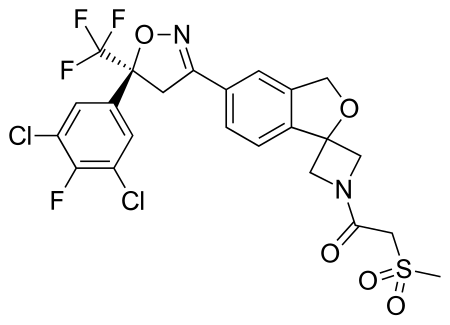
Chemical compound SarolanerClinical dataTrade namesSimparicaOther namesPF-6450567ATCvet codeQP53BE03 (WHO) Legal statusLegal status US: ℞-only[1] Identifiers IUPAC name 1-[6-[(5S)-5-(3,5-Dichloro-4-fluorophenyl)-5-(trifluoromethyl)-4H-1,2-oxazol-3-yl]spiro[1H-2-benzofuran-3,3'-azetidine]-1'-yl]-2-methylsulfonylethanone CAS Number1398609-39-6PubChem CID73169092ChemSpider31458198UNIIDM113FTW7FKEGGD10668ChEMBLChEMBL3137302ECHA InfoCard100.234.000 Chemical and physical da...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Interior of a Romanesque Church J. M. W. Turner – news · newspapers · books · scholar · JSTOR (April 2023) Interior of a Romanesque Church (c. 1795-1800) by Turner Interior of a Romanesque Church is an oil on mahoganey painting by J. M. W. ...

Favio Posca Información personalNombre de nacimiento Favio Juan Manuel PoscaNacimiento 22 de diciembre de 1966 (56 años)Mar del Plata, Buenos Aires, ArgentinaNacionalidad ArgentinoFamiliaCónyuge María Luisa CallauHijos Manuela RoccoInformación profesionalOcupación Actor HumoristaSitio web www.favioposca.com[editar datos en Wikidata] Favio Juan Manuel Posca (22 de diciembre de 1966; Mar del Plata, Buenos Aires, Argentina) es un actor y humorista argentino que alcanzó gran...

Sociedad Patriótica de 1789Société patriotique de 1789 Fundación 1790Disolución 1791Ideología Monarquía constitucionalLiberalismo clásico[1]Liberalismo conservadorModerantismoPosición Centro[2]Sucesor Club des FeuillantsSede Palais-Royal, ParísPaís FranciaColores Gris[editar datos en Wikidata] El Club de 1789, de nombre completo Club Patriótico de 1789 o Sociedad Patriótica de 1789 (del francés: Club de 1789, Société patriotique...

Sari Pangantin atau Sari Pengantin adalah kue tradisional yang berasal dari masyarakat suku Banjar di Kalimantan Selatan namun juga terdapat di daerah lainnya seperti di Kalimantan Timur. Kue ini serupa dengan kue talam, namun yang membedakan adalah kue Sari Pangantin terdiri dari 3 lapis yang berwarna-warni. Kue ini terbuat dari adonan tepung beras yang dikukus. Kue Sari Pangantin biasanya dapat ditemui saat bulan Ramadan sebagai takjil untuk berbuka puasa [1]. Namun, kue ini juga bi...

لمعانٍ أخرى، طالع الحصين (توضيح). الحصين (محلة) تقسيم إداري البلد اليمن المحافظة محافظة إب المديرية مديرية السبرة العزلة عزلة بلادالشعيبي السفلى القرية قرية الشاجبة السكان التعداد السكاني 2004 السكان 37 • الذكور 18 • الإناث 19 • عدد الأسر 4 • عدد المسا�...

GagodohGagodoh dengan isi potongan pisangNama lainGaguduh, Sanggar, CakodokTempat asalIndonesiaDaerahKalimantan, LampungSuhu penyajianpanas setelah digorengBahan utamaTepung terigu, gula, garam, kapur, air Gagodoh atau Gaguduh (nama lain: Sanggar atau Cakodok) adalah sejenis kue khas Indonesia, terutama di Kalimantan Selatan dan Kalimantan Timur dan Lampung. Bentuknya semacam perkedel. Gagodoh terbuat dari tepung terigu, gula, garam, kapur, dan air. Untuk isi dari Gagodoh tersebut, biasanya m...

TrentinaraKomuneComune di TrentinaraLokasi Trentinara di Provinsi SalernoNegara ItaliaWilayah CampaniaProvinsiSalerno (SA)Luas[1] • Total23,44 km2 (9,05 sq mi)Ketinggian[2]606 m (1,988 ft)Populasi (2016)[3] • Total1.683 • Kepadatan72/km2 (190/sq mi)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos84070Kode area telepon0828Situs webhttp://www.comune.trentinara.sa.it Trent...

جامعة كاليفورنيا الجنوبية University of Southern California شعار جامعة كاليفورنيا الجنوبية الشعار Palmam qui meruit ferat (باللاتينية) معلومات التأسيس 1880 المنحة المالية 4.5 مليار $[1] النوع جامعة خاصة تكاليف الدراسة 48,280 $ الموقع الجغرافي إحداثيات 34°01′18″N 118°17′07″W / 34.021667°N 118.285278°W / 34...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (فبراير 2023) فهد بن دحيم معلومات شخصية الميلاد القرن 13هـ/ 19مالرياض تاريخ الوفاة القرن 14هـ/ 20م الجنسية السعودية الديانة مسلم الحياة العملية سبب الشهرة شاعر الخدمة الع...

Nahwitti was a Kwakwakaʼwakw First Nation village and a major trading site during the maritime fur trade era of approximately 1790 to 1850. Today it is an Indian reserve under the administration of the Kwakwakaʼwakw Tlatlasikwala Nation. It is located near the northern tip of Vancouver Island, at Cape Sutil on Queen Charlotte Sound, near Hope Island and the Nahwitti River, east of Cape Scott,[1] and not far from historic Fort Rupert and modern Port Hardy.The North West Coast during ...

Ancient Roman god of desire, affection and erotic love For other uses, see Cupid (disambiguation) and Eros (disambiguation). CupidGod of desire, erotic love, attraction, and affectionClassical statue of Cupid with his bowSymbolBow and arrowMountDolphinPersonal informationParentsMars and VenusConsortPsycheChildrenVoluptasEquivalentsGreek equivalentErosHinduism equivalentKamadeva Part of a series onLoveRed-outline heart icon Types of love Affection Bonding Broken heart Compassionate love Conjug...

Park Chung-hee 박정희Presiden Korea Selatan 3Masa jabatan17 Desember 1963 (Ketua SCNR 1961-63) – 26 Oktober 1979Perdana MenteriChoi Doo Sun Chung Il Kwon Baek Du-jin Kim Jong Pil Choi Kyu HahPendahuluYoon Po-sonPenggantiChoi Kyu-haKetua Dewan Tertinggi untuk Rekonstruksi NasionalMasa jabatanJuli 3, 1961 – Desember 17, 1963Wakil Ketua dari Mei 16, 1961PendahuluChang Do-yongPenggantiKantor Bangkrut Informasi pribadiLahir30 September 1917Gumi-si, Gyeongsang Utara, Jepang-Berk...

Argentine sports club This article is about the Argentine basketball team. For the Uruguayan football team, see Peñarol. Peñarol (MDP)NicknameMilrayitas (thousand-strips)LeaguesLNBFounded7 November 1922; 101 years ago (1922-11-07)ArenaPolideportivo Islas MalvinasLocationMar del Plata, Buenos Aires Province, ArgentinaTeam colors PresidentDomingo RoblesHead coachLeonardo GutiérrezChampionships5 Argentine championships2 FIBA Americas League2 Torneo InterLigas3 To...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (March 2011) (Learn how and when to remove this template message) A woodblock print depicting the wife of Onodera Junai, one of the forty-seven rōnin. She prepares herself to follow her husband into death. Junshi (殉死, following the lord in death, sometimes translated as ...

College football game1984 Rose Bowl70th Rose Bowl Game UCLA Bruins Illinois Fighting Illini (6–4–1) (10–1) 45 9 Head coach: Terry Donahue Head coach: Mike White APCoaches 45 1234 Total UCLA 721107 45 Illinois 0306 9 DateJanuary 2, 1984Season1983StadiumRose BowlLocationPasadena, CaliforniaMVPRick Neuheisel (UCLA QB)FavoriteIllinois by 4½ points[1]National anthemUCLA's The Solid Gold Sound BandRefereeJohn Nealon (Big Ten)(split crew: Big Ten, Pac-10)Halftime s...

1826 Rhode Island gubernatorial election ← 1825 April 19, 1826[1][2] 1827 → Nominee James Fenner Party Democratic-Republican Popular vote 1,731 Percentage 100% Governor before election James Fenner Democratic-Republican Elected Governor James Fenner Democratic-Republican The 1826 Rhode Island gubernatorial election was an uncontested election held on April 19, 1826 to elect the Governor of Rhode Island. James Fenner, the incumbent governor and...

This article is about the video game series. For the first game in the series, see Road Rash (1991 video game). For the second game in the series, titled Road Rash for the GBC, see Road Rash II. For the third game in the series, see Road Rash (1994 video game). For the medical condition, see road rash. Video game seriesRoad RashGenre(s)RacingDeveloper(s)Electronic Arts Electronic Arts MobilePublisher(s)Electronic Arts Electronic Arts MobileFirst releaseRoad RashSeptember 1991Latest releaseRoa...

1989 single by Metallica This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (December 2016) (Learn how and when to remove this template message) OneSingle by Metallicafrom the album ...And Justice for All B-sideThe Prince (7)ReleasedJanuary 10, 1989 (1989-01-10)RecordedOne on One (Los Angeles)GenreThrash metalLength 7:27 (album version) 5...






