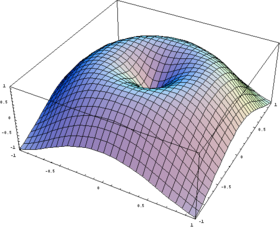
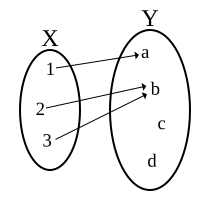
Функція (математика)
| |||||||||||||||||||||||||||
Read other articles:

جان فيليب دوراند (بالفرنسية: Jean-Philippe Durand) معلومات شخصية الميلاد 11 نوفمبر 1960 (العمر 63 سنة)ليون الطول 1.77 م (5 قدم 9 1⁄2 بوصة) مركز اللعب وسط الجنسية فرنسا مسيرة الشباب سنوات فريق تولوز 1980-1981 تولوز المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1981–1989 تولوز 195 (26) 1989–1991 جي

American musician, songwriter, arranger, and record producer (born 1943) Van Dyke ParksParks performing at Primavera Sound 2010Background informationBorn (1943-01-03) January 3, 1943 (age 80)Hattiesburg, Mississippi, U.S.OriginLos Angeles, California, U.S.Genres Orchestral pop[1] Americana[2] art pop[3] baroque pop[4] experimental pop[5] Occupation(s) Composer songwriter arranger performer record producer director actor Instrument(s) Keyboards acco...

Sports teams of Alabama A&M University Alabama A&M Bulldogs and Lady BulldogsUniversityAlabama A&M UniversityConferenceSouthwestern Athletic ConferenceNCAADivision I (FCS)Athletic directorDr. Paul A. BryantLocationNormal, AlabamaVarsity teams15Football stadiumLouis Crews StadiumArenaAlabama A&M Events CenterNicknameBulldogsLady BulldogsColorsMaroon and white[1] Websitewww.aamusports.com The Alabama A&M Bulldogs and Lady Bulldogs are ...

American judge For the Connecticut legislator, see William Woodbridge (Connecticut physician). For the educator (1755-1836), see William Woodbridge (educator). Senator Woodbridge redirects here. For the Vermont State Senate member, see Frederick E. Woodbridge. This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (February 2013)...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2017) رون سيكسميث معلومات شخصية الميلاد 8 يناير 1964 (59 سنة)[1] سانت كاثرينز[2][3] الإقامة تورونتوسانت كاثرينز مواطنة كندا الحياة الفنية ال

Петі-НуарPetit-Noir Країна Франція Регіон Бургундія-Франш-Конте Департамент Жура Округ Доль Кантон Шемен Код INSEE 39415 Поштові індекси 39120 Координати 46°56′17″ пн. ш. 5°20′34″ сх. д.H G O Висота 177 - 215 м.н.р.м. Площа 20,52 км² Населення 1093 (01-2020[1]) Густота 55,41 ос./км² Роз

Pour les articles homonymes, voir Turkestan. Cet article est une ébauche concernant une localité kazakhe. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Turkestan Mausolée de Ahmed Yasavi Administration Pays Kazakhstan Province (oblys) Kazakhstan-Méridional Démographie Population 142 899 hab. (2009[1]) Géographie Coordonnées 43° 17′ 42″ nord, 68° 15′ 31″ e...

Salamandra-lusitânica Estado de conservação Vulnerável (IUCN 3.1) [1] Classificação científica Reino: Animalia Filo: Chordata Classe: Amphibia Ordem: Caudata Família: Salamandridae Género: ChioglossaBocage, 1864 Espécie: C. lusitanica Nome binomial Chioglossa lusitanicaBocage, 1864 Distribuição geográfica Distribuição actual de Salamandra-lusitânica. Subespécies C. l. lusitanica Bocage, 1864 C. l. longipes Arntzen, Groenenberg, Alexandrino, Ferrand e Sequeira, 2007 A salamand...

青雲中学校・高等学校 北緯32度49分44.2秒 東経129度50分14.3秒 / 北緯32.828944度 東経129.837306度 / 32.828944; 129.837306座標: 北緯32度49分44.2秒 東経129度50分14.3秒 / 北緯32.828944度 東経129.837306度 / 32.828944; 129.837306国公私立の別 私立学校設置者 学校法人青雲学園校訓 いまをだいじに設立年月日 1974年10月創立者 速見雄吉共学・別学 共学中高一貫教育 ...

Species of mammal Japanese mole[1] Conservation status Least Concern (IUCN 3.1)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Eulipotyphla Family: Talpidae Genus: Mogera Species: M. wogura Binomial name Mogera wogura(Temminck, 1842) Japanese mole range Synonyms Mogera kobeae Thomas, 1905 The Japanese mole (Mogera wogura), also known as Temminck's mole, is a species of mole endemic to Japan.[3] A solit...

French tennis player Tatiana GolovinGolovin at UNESCO Headquarters in ParisCountry (sports) FranceResidenceNew York, U.S.[1]Born (1988-01-25) 25 January 1988 (age 35)Moscow, Soviet UnionHeight1.75 m (5 ft 9 in)Turned pro2002Retired2008 (first retire), 2019 (second retire)PlaysRight-handed (two-handed backhand)Prize moneyUS$ 1,923,053SinglesCareer record165–93 (64.0%)Career titles2Highest rankingNo. 12 (4 February 2008)Grand Slam sing...

Teile dieses Artikels scheinen seit 2015 nicht mehr aktuell zu sein. Bitte hilf uns dabei, die fehlenden Informationen zu recherchieren und einzufügen. Wikipedia:WikiProjekt Ereignisse/Vergangenheit/fehlend Start eines Prototyps des Ground-Based Interceptors auf einer PLV-Rakete (2001) Prototyp des „Exoatmospheric Kill Vehicle“ Die National Missile Defense (NMD; deutsch Nationale Raketenabwehr) bzw. der US-Raketenschild ist ein zur Regierungszeit von US-Präsident George W. Bush angestre...

Sertifikat Hak Milik atau disingkat SHM adalah jenis sertifikat yang pemiliknya memiliki hak penuh atas kepemilikan tanah pada kawasan dengan luas tertentu yang telah disebutkan dalam sertifikat tersebut. Berbeda dengan Sertifikat Hak Guna Bangunan yang memiliki batas waktu tertentu, Sertifikat Hak Milik tidak ada batas waktu kepemilikan. Sertifikat ini dikeluarkan oleh Badan Pertanahan Nasional. Sertifikat Hak Milik (SHM) hanya dapat dimiliki oleh Warna Negara Indonesia[1], dan tidak...

Île aux Cygnes nhìn từ tháp Eiffel Île aux Cygnes là một hòn đảo nhân tạo trên sông Seine, thuộc thành phố Paris. Tên của đảo thường được dịch sang tiếng Việt là Đảo Thiên Nga. Trong tiếng Pháp, hòn đảo này còn được viết là Île aux Cygnes hay cũ hơn có tên Digue de Grenelle, có nghĩa Đê Grenelle. Là hòn đảo nhân tạo, Île aux Cygnes dài 890 mét nhưng bề ngang chỉ 11 mét. Nằm giữa Quận 15 và Quận 1...

Venezuelan prelate His EminenceBaltazar Enrique Porras CardozoCardinal, Metropolitan Archbishop of CaracasChurchRoman Catholic ChurchArchdioceseCaracasSeeCaracasAppointed9 July 2018 (apostolic administrator)Installed17 January 2023PredecessorJorge Liberato Urosa SavinoOther post(s)Cardinal-Priest of Santi Giovanni Evangelista e Petronio (2016–)OrdersOrdination30 July 1967by Miguel Antonio Salas SalasConsecration17 September 1983by José Lebrún MoratinosCreated cardinal19 November...

Bắc Trà My Huyện Huyện Bắc Trà My Trụ sở UBND huyện Bắc Trà MyHành chínhQuốc gia Việt NamVùngDuyên hải Nam Trung BộTỉnhQuảng NamHuyện lỵthị trấn Trà MyPhân chia hành chính1 thị trấn, 12 xãThành lập20/6/2003[1]Địa lýTọa độ: 15°20′4″B 108°12′35″Đ / 15,33444°B 108,20972°Đ / 15.33444; 108.20972 Bản đồ huyện Bắc Trà My Bắc Trà My Vị trí huyện Bắc Trà My trên bản đ�...

The highly decorated two-storey porch of St Mary's, Yatton, England[1][2] A church porch is a room-like structure at a church's main entrance.[3] A porch protects from the weather to some extent. Some porches have an outer door, others a simple gate, and in some cases the outer opening is not closed in any way. The porch at St Wulfram's Church, Grantham, like many others of the period, has a room above the porch. It once provided lodging for the priest, but now houses ...

Railway station in Manitoba, Canada McCrearyThe station circa 1913General informationLocationRailway St. (between 1st & 2nd Avenues), McCreary, ManitobaCoordinates50°46′25″N 99°29′23″W / 50.7735°N 99.4897°W / 50.7735; -99.4897Line(s)Winnipeg – Churchill trainPlatforms1Tracks1ConstructionStructure typeSign postPlatform levels1HistoryOpened1912Services Preceding station Via Rail Following station Lauriertoward Churchill Winnipeg–Churchill Glenellatowa...

University in Egypt This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Future University in Egypt – news · newspapers · books · scholar · JSTOR (August 2011) (Learn how and when to remove this template message) Future University in Egypt جامعة المستقبلTypePrivateEstablished2006ChairmanKhaled Hassan AzazyPresidentEbada SarhanAddressEnd of 90th ...

Genus of legumes Retama White flowers of Retama rhodorhizoides Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Fabales Family: Fabaceae Subfamily: Faboideae Clade: Core Genistoids Tribe: Genisteae Genus: RetamaRaf. Species 4–14; see text. Synonyms[1] Boelia Webb (1853) Lygos Adans. (1763), nom. rej. Retama (also known as rotem, Hebrew: רותם) is a genus of flowering bushes in the legume family, Fabaceae. It b...