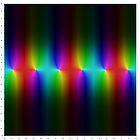
–Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł
–ó–į–Ņ—Ä–ĺ—Ā—č ¬ęsin¬Ľ –ł ¬ę—Ā–ł–Ĺ—É—Ā¬Ľ –Ņ–Ķ—Ä–Ķ–Ĺ–į–Ņ—Ä–į–≤–Ľ—Ź—é—ā—Ā—Ź —Ā—é–ī–į; —É —ā–Ķ—Ä–ľ–ł–Ĺ–ĺ–≤
sin –ł
—Ā–ł–Ĺ—É—Ā –Ķ—Ā—ā—Ć —ā–į–ļ–∂–Ķ –ī—Ä—É–≥–ł–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź.
–†–ł—Ā. 1. –ď—Ä–į—Ą–ł–ļ–ł —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ: –Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–łŐĀ—á–Ķ—Ā–ļ–ł–Ķ —Ą—ÉŐĀ–Ĺ–ļ—Ü–ł–ł ‚ÄĒ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł [ 1] –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ –ł –≤—č—Ä–į–∂–į–Ľ–ł –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ī–Ľ–ł–Ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ —ć—ā–ł—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ –ĺ—ā –ĺ—Ā—ā—Ä—č—Ö —É–≥–Ľ–ĺ–≤ –Ņ—Ä–ł –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–Ķ (–ł–Ľ–ł, —á—ā–ĺ —Ä–į–≤–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ, –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā—Ć —Ö–ĺ—Ä–ī –ł –≤—č—Ā–ĺ—ā –ĺ—ā —Ü–Ķ–Ĺ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į –ī—É–≥–ł –≤ –ļ—Ä—É–≥–Ķ ). –≠—ā–ł —Ą—É–Ĺ–ļ—Ü–ł–ł –Ĺ–į—ą–Ľ–ł —ą–ł—Ä–ĺ–ļ–ĺ–Ķ –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –≤ —Ā–į–ľ—č—Ö —Ä–į–∑–Ĺ—č—Ö –ĺ–Ī–Ľ–į—Ā—ā—Ź—Ö –Ĺ–į—É–ļ–ł. –ü–ĺ –ľ–Ķ—Ä–Ķ —Ä–į–∑–≤–ł—ā–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ī—č–Ľ–ĺ —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ĺ, –≤ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–ľ –Ņ–ĺ–Ĺ–ł–ľ–į–Ĺ–ł–ł –ł—Ö –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–ľ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–Ķ –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ķ –ł–Ľ–ł –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ .
–†–į–∑–ī–Ķ–Ľ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł, –ł–∑—É—á–į—é—Č–ł–Ļ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ, –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ .
–ö —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–ľ —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ —ā—Ä–į–ī–ł—Ü–ł–ĺ–Ĺ–Ĺ–ĺ –Ņ—Ä–ł—á–ł—Ā–Ľ—Ź—é—ā:
–Ņ—Ä—Ź–ľ—č–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł: —Ā–ł–Ĺ—É—Ā (
sin
‚Ā° -->
x
{\displaystyle \sin x}
–ļ–ĺ—Ā–ł–Ĺ—É—Ā (
cos
‚Ā° -->
x
{\displaystyle \cos x}
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł: —ā–į–Ĺ–≥–Ķ–Ĺ—Ā
(
t
g
x
=
sin
‚Ā° -->
x
cos
‚Ā° -->
x
)
{\displaystyle \left(\mathrm {tg} \,x={\frac {\sin x}{\cos x}}\right)}
–ļ–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā
(
c
t
g
x
=
cos
‚Ā° -->
x
sin
‚Ā° -->
x
)
{\displaystyle \left(\mathrm {ctg} \,x={\frac {\cos x}{\sin x}}\right)}
—Ā–Ķ–ļ–į–Ĺ—Ā
(
sec
‚Ā° -->
x
=
1
cos
‚Ā° -->
x
)
{\displaystyle \left(\sec x={\frac {1}{\cos x}}\right)}
–ļ–ĺ—Ā–Ķ–ļ–į–Ĺ—Ā
(
c
o
s
e
c
x
=
1
sin
‚Ā° -->
x
)
{\displaystyle \left(\mathrm {cosec} \,x={\frac {1}{\sin x}}\right)}
–ĺ–Ī—Ä–į—ā–Ĺ—č–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł :–į—Ä–ļ—Ā–ł–Ĺ—É—Ā, –į—Ä–ļ–ļ–ĺ—Ā–ł–Ĺ—É—Ā, –į—Ä–ļ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā, –į—Ä–ļ–ļ–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā, –į—Ä–ļ—Ā–Ķ–ļ–į–Ĺ—Ā –ł –į—Ä–ļ–ļ–ĺ—Ā–Ķ–ļ–į–Ĺ—Ā. –ö—Ä–ĺ–ľ–Ķ —ć—ā–ł—Ö —ą–Ķ—Ā—ā–ł —ą–ł—Ä–ĺ–ļ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ—č—Ö —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ, –ł–Ĺ–ĺ–≥–ī–į –≤ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ä–Ķ–ī–ļ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—č–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł (–≤–Ķ—Ä—Ā–ł–Ĺ—É—Ā –ł —ā. –ī.).
–°–ł–Ĺ—É—Ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ķ—Ā–ļ–ł–Ķ, –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č–Ķ –ł –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä—É–Ķ–ľ—č–Ķ –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł. –ě—Ā—ā–į–Ľ—Ć–Ĺ—č–Ķ —á–Ķ—ā—č—Ä–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ĺ–į –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –ĺ—Ā–ł —ā–į–ļ–∂–Ķ –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ—č, –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ĺ—č –ł –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä—É–Ķ–ľ—č, –∑–į –ł—Ā–ļ–Ľ—é—á–Ķ–Ĺ–ł–Ķ–ľ —Ā—á—Ď—ā–Ĺ–ĺ–≥–ĺ —á–ł—Ā–Ľ–į —Ä–į–∑—Ä—č–≤–ĺ–≤ –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į : —É —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į –ł —Ā–Ķ–ļ–į–Ĺ—Ā–į –≤ —ā–ĺ—á–ļ–į—Ö
± ¬Ī -->
π ŌÄ -->
n
+
π ŌÄ -->
2
{\displaystyle \pm \pi n+{\frac {\pi }{2}}}
± ¬Ī -->
π ŌÄ -->
n
{\displaystyle \pm \pi n}
–ď—Ä–į—Ą–ł–ļ–ł —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ņ–ĺ–ļ–į–∑–į–Ĺ—č –Ĺ–į —Ä–ł—Ā. 1.
–†–ł—Ā. 2. –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ě–Ī—č—á–Ĺ–ĺ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā—Ā—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł[ 2] –ī–Ķ–ļ–į—Ä—ā–ĺ–≤–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ĺ–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–≥–ĺ —Ä–į–ī–ł—É—Ā–į (
R
=
1
{\displaystyle R=1}
O
{\displaystyle O}
—É–≥–ĺ–Ľ —Ā—ā–į–Ĺ–Ķ–ľ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –Ņ–ĺ–≤–ĺ—Ä–ĺ—ā –ĺ—ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –ĺ—Ā–ł –į–Ī—Ā—Ü–ł—Ā—Ā –ī–ĺ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –Ľ—É—á–į
O
B
{\displaystyle OB}
B
{\displaystyle B}
–ź–Ī—Ā—Ü–ł—Ā—Ā—É —ā–ĺ—á–ļ–ł
B
{\displaystyle B}
x
B
{\displaystyle x_{B}}
–ĺ—Ä–ī–ł–Ĺ–į—ā—É ‚ÄĒ
y
B
{\displaystyle y_{B}}
–†–ł—Ā. 3. –ß–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —É–≥–Ľ–į
α őĪ -->
{\displaystyle \alpha }
—ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ä–į–ī–ł—É—Ā–ĺ–ľ, —Ä–į–≤–Ĺ—č–ľ –Ķ–ī–ł–Ĺ–ł—Ü–Ķ –°–ł–Ĺ—É—Ā–ĺ–ľ —É–≥–Ľ–į
α őĪ -->
{\displaystyle \alpha }
M
α őĪ -->
{\displaystyle M_{\alpha }}
(
⋅ ‚čÖ -->
)
M
α őĪ -->
{\displaystyle {\left(\cdot \right)}M_{\alpha }}
(
⋅ ‚čÖ -->
)
M
0
{\displaystyle {\left(\cdot \right)}M_{0}}
α őĪ -->
{\displaystyle \alpha }
α őĪ -->
>
0
{\displaystyle \alpha >0}
α őĪ -->
<
0
{\displaystyle \alpha <0}
–ö–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–ľ —É–≥–Ľ–į
α őĪ -->
{\displaystyle \alpha }
M
α őĪ -->
{\displaystyle M_{\alpha }}
(
⋅ ‚čÖ -->
)
M
α őĪ -->
{\displaystyle {\left(\cdot \right)}M_{\alpha }}
(
⋅ ‚čÖ -->
)
M
0
{\displaystyle {\left(\cdot \right)}M_{0}}
α őĪ -->
{\displaystyle \alpha }
α őĪ -->
>
0
{\displaystyle \alpha >0}
α őĪ -->
<
0
{\displaystyle \alpha <0}
–Ę–į–Ĺ–≥–Ķ–Ĺ—Ā–ĺ–ľ —É–≥–Ľ–į
α őĪ -->
{\displaystyle \alpha }
M
α őĪ -->
{\displaystyle M_{\alpha }}
M
α őĪ -->
{\displaystyle M_{\alpha }}
–ö–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā–ĺ–ľ —É–≥–Ľ–į
α őĪ -->
{\displaystyle \alpha }
M
α őĪ -->
{\displaystyle M_{\alpha }}
M
α őĪ -->
{\displaystyle M_{\alpha }}
[ 3]
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –≤—č–≥–Ľ—Ź–ī—Ź—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
sin
‚Ā° -->
α őĪ -->
=
y
B
{\displaystyle \sin \alpha =y_{B}}
cos
‚Ā° -->
α őĪ -->
=
x
B
{\displaystyle \cos \alpha =x_{B}}
tg
‚Ā° -->
α őĪ -->
=
y
B
x
B
{\displaystyle \operatorname {tg} \alpha ={\frac {y_{B}}{x_{B}}}}
ctg
‚Ā° -->
α őĪ -->
=
x
B
y
B
{\displaystyle \operatorname {ctg} \alpha ={\frac {x_{B}}{y_{B}}}}
sec
‚Ā° -->
α őĪ -->
=
1
x
B
{\displaystyle \sec \alpha ={\frac {1}{x_{B}}}}
cosec
‚Ā° -->
α őĪ -->
=
1
y
B
{\displaystyle \operatorname {cosec} \alpha ={\frac {1}{y_{B}}}}
–Ě–Ķ—ā—Ä—É–ī–Ĺ–ĺ –≤–ł–ī–Ķ—ā—Ć, —á—ā–ĺ —ā–į–ļ–ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ā–į–ļ–∂–Ķ –ĺ—Ā–Ĺ–ĺ–≤—č–≤–į–Ķ—ā—Ā—Ź –Ĺ–į –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź—Ö –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —Ā —ā–Ķ–ľ –ĺ—ā–Ľ–ł—á–ł–Ķ–ľ, —á—ā–ĺ —É—á–ł—ā—č–≤–į–Ķ—ā—Ā—Ź –∑–Ĺ–į–ļ (
± ¬Ī -->
1
{\displaystyle \pm 1}
R
{\displaystyle R}
–Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł .
–í —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł–ł —É–ī–ĺ–Ī–Ĺ—č–ľ –ĺ–ļ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –≤–Ķ—Ā—ā–ł —Ā—á—Ď—ā —É–≥–Ľ–ĺ–≤ –Ĺ–Ķ –≤ –≥—Ä–į–ī—É—Ā–Ĺ–ĺ–Ļ –ľ–Ķ—Ä–Ķ, –į –≤ —Ä–į–ī–ł–į–Ĺ–Ĺ–ĺ–Ļ . –Ę–į–ļ, —É–≥–ĺ–Ľ –≤
360
∘ ‚ąė -->
{\displaystyle 360^{\circ }}
2
π ŌÄ -->
{\displaystyle 2\pi }
180
∘ ‚ąė -->
{\displaystyle 180^{\circ }}
π ŌÄ -->
{\displaystyle \pi }
2
π ŌÄ -->
{\displaystyle 2\pi }
α őĪ -->
{\displaystyle \alpha }
α őĪ -->
{\displaystyle \alpha }
–Ě–į–ļ–ĺ–Ĺ–Ķ—Ü, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–ľ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —á–ł—Ā–Ľ–į
x
{\displaystyle x}
—Ä–į–ī–ł–į–Ĺ–Ĺ–į—Ź –ľ–Ķ—Ä–į –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–į–≤–Ĺ–į
x
{\displaystyle x}
–†–ł—Ā. 4. –Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ĺ—Ā—ā—Ä–ĺ–≥–ĺ —É–≥–Ľ–į –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į. –ú–į—Ä–ļ–į –°–°–°–† 1961 –≥–ĺ–ī–į –í –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ĺ—Ā—ā—Ä–ĺ–≥–ĺ —É–≥–Ľ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā—Ā—Ź –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź–ľ–ł —Ā—ā–ĺ—Ä–ĺ–Ĺ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į [ 4]
△ ‚Ė≥ -->
A
O
B
{\displaystyle \triangle AOB}
∠ ‚ą† -->
A
{\displaystyle \angle A}
∠ ‚ą† -->
A
O
B
=
α őĪ -->
{\displaystyle \angle AOB=\alpha }
O
B
{\displaystyle OB}
sin
‚Ā° -->
α őĪ -->
=
A
B
O
B
{\displaystyle \sin \alpha ={\frac {AB}{OB}}}
α őĪ -->
{\displaystyle \alpha }
–ļ–į—ā–Ķ—ā–į –ļ –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–Ķ ). –°–ł–Ĺ—É—Ā –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ ¬ę–ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā —Ā–∂–į—ā–ł—Ź¬Ľ –ī–Ľ–ł–Ĺ—č –ĺ—ā—Ä–Ķ–∑–ļ–į –Ņ—Ä–ł –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł–ł –∑–į –Ĺ–ł–ľ –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ, —ā–ĺ –Ķ—Ā—ā—Ć –Ĺ–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ —É–ļ–ĺ—Ä–į—á–ł–≤–į–Ķ—ā—Ā—Ź –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź –ĺ—ā—Ä–Ķ–∑–ļ–į –Ņ—Ä–ł –Ķ–≥–ĺ –Ĺ–į–ļ–Ľ–ĺ–Ĺ–Ķ –Ĺ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–Ļ —É–≥–ĺ–Ľ[ 5]
cos
‚Ā° -->
α őĪ -->
=
O
A
O
B
{\displaystyle \cos \alpha ={\frac {OA}{OB}}}
α őĪ -->
{\displaystyle \alpha }
–ļ–į—ā–Ķ—ā–į –ļ –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–Ķ );
t
g
α őĪ -->
=
A
B
O
A
{\displaystyle \mathrm {tg} \,\alpha ={\frac {AB}{OA}}}
α őĪ -->
{\displaystyle \alpha }
–ļ–į—ā–Ķ—ā–į –ļ –Ņ—Ä–ł–Ľ–Ķ–∂–į—Č–Ķ–ľ—É). –Ę–į–Ĺ–≥–Ķ–Ĺ—Ā –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –ľ–į—Ā—ą—ā–į–Ī–ł—Ä—É—é—Č–ł–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –ł–Ľ–ł –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź: –Ĺ–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ľ–Ķ–∂–į—Č–ł–Ļ –ļ–į—ā–Ķ—ā –Ī–ĺ–Ľ—Ć—ą–Ķ –Ņ—Ä–ł–Ľ–Ķ–∂–į—Č–Ķ–≥–ĺ. –ē—Ā–Ľ–ł —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —Ä–į–≤–Ķ–Ĺ 1, —ā–ĺ –ļ–į—ā–Ķ—ā—č —Ä–į–≤–Ĺ—č. –Ē–į–Ĺ–Ĺ–ĺ–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ –į–Ĺ–į–Ľ–ł–∑–Ķ –≤ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ: –Ĺ–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –Ķ–ī–ł–Ĺ–ł—Ü—č –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź –ĺ—Ä–ī–ł–Ĺ–į—ā—č –Ī–ĺ–Ľ—Ć—ą–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –Ķ–ī–ł–Ĺ–ł—Ü—č –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź –į–Ī—Ā—Ü–ł—Ā—Ā—č. –ē—Ā–Ľ–ł —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —Ä–į–≤–Ķ–Ĺ 1, —ā–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –Ķ–ī–ł–Ĺ–ł—Ü –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź —Ä–į–≤–Ĺ—č. –í –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–Ķ–∑—Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ (–ī–Ľ–ł–Ĺ–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ľ–Ķ–∂–į—Č–Ķ–≥–ĺ –ļ–į—ā–Ķ—ā–į ‚ąē –ī–Ľ–ł–Ĺ–į –Ņ—Ä–ł–Ľ–Ķ–∂–į—Č–Ķ–≥–ĺ –ļ–į—ā–Ķ—ā–į, –ľ ‚ąē –ľ), –Ĺ–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ļ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—é –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā –ľ–ĺ–∂–Ķ—ā –ł–ľ–Ķ—ā—Ć —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć —ā–Ķ–Ľ–į –Ķ—Ā—ā—Ć –Ņ—É—ā—Ć ‚ąē –≤—Ä–Ķ–ľ—Ź, —ā–ĺ –Ķ—Ā—ā—Ć –ľ ‚ąē —Ā.
c
t
g
α őĪ -->
=
O
A
A
B
{\displaystyle \mathrm {ctg} \,\alpha ={\frac {OA}{AB}}}
α őĪ -->
{\displaystyle \alpha }
–ļ–į—ā–Ķ—ā–į –ļ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ľ–Ķ–∂–į—Č–Ķ–ľ—É);
s
e
c
α őĪ -->
=
O
B
O
A
{\displaystyle \mathrm {sec} \,\alpha ={\frac {OB}{OA}}}
α őĪ -->
{\displaystyle \alpha }
–≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑—č –ļ –Ņ—Ä–ł–Ľ–Ķ–∂–į—Č–Ķ–ľ—É –ļ–į—ā–Ķ—ā—É ) .
c
o
s
e
c
α őĪ -->
=
O
B
A
B
{\displaystyle \mathrm {cosec} \,\alpha ={\frac {OB}{AB}}}
α őĪ -->
{\displaystyle \alpha }
–≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑—č –ļ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ľ–Ķ–∂–į—Č–Ķ–ľ—É –ļ–į—ā–Ķ—ā—É ).–Ē–į–Ĺ–Ĺ–ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ł–ľ–Ķ–Ķ—ā –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ –ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ņ—Ä–Ķ–ł–ľ—É—Č–Ķ—Ā—ā–≤–ĺ, —ā–į–ļ –ļ–į–ļ –Ĺ–Ķ —ā—Ä–Ķ–Ī—É–Ķ—ā –≤–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –Ĺ–ĺ —ā–į–ļ–∂–Ķ –ł —ā–į–ļ–ĺ–Ļ –ļ—Ä—É–Ņ–Ĺ—č–Ļ –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ĺ–ļ, —á—ā–ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ī–į–∂–Ķ –ī–Ľ—Ź —ā—É–Ņ—č—Ö —É–≥–Ľ–ĺ–≤, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –∑–Ĺ–į—ā—Ć –Ņ—Ä–ł —Ä–Ķ—ą–Ķ–Ĺ–ł–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č—Ö –∑–į–ī–į—á –ĺ —ā—É–Ņ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į—Ö. (–°–ľ.: —ā–Ķ–ĺ—Ä–Ķ–ľ–į —Ā–ł–Ĺ—É—Ā–ĺ–≤ , —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤ ).
–°–ł–Ĺ—É—Ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –ļ–į–ļ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł, –≤—ā–ĺ—Ä—č–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ä–į–≤–Ĺ—č —Ā–į–ľ–ł–ľ —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ, –≤–∑—Ź—ā—č–ľ —Ā–ĺ –∑–Ĺ–į–ļ–ĺ–ľ –ľ–ł–Ĺ—É—Ā:
(
cos
‚Ā° -->
x
)
″
=
− ‚ąí -->
cos
‚Ā° -->
x
,
{\displaystyle \ \left(\cos x\right)''=-\cos x,}
(
sin
‚Ā° -->
x
)
″
=
− ‚ąí -->
sin
‚Ā° -->
x
.
{\displaystyle \ \left(\sin x\right)''=-\sin x.}
–Ę–ĺ –Ķ—Ā—ā—Ć –∑–į–ī–į—ā—Ć –ł—Ö –ļ–į–ļ —á—Ď—ā–Ĺ–ĺ–Ķ (–ļ–ĺ—Ā–ł–Ĺ—É—Ā) –ł –Ĺ–Ķ—á—Ď—ā–Ĺ–ĺ–Ķ (—Ā–ł–Ĺ—É—Ā) —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź
d
2
d
φ ŌÜ -->
2
R
(
φ ŌÜ -->
)
=
− ‚ąí -->
R
(
φ ŌÜ -->
)
,
{\displaystyle {\frac {d^{2}}{d\varphi ^{2}}}R(\varphi )=-R(\varphi ),}
—Ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł —É—Ā–Ľ–ĺ–≤–ł—Ź–ľ–ł:
R
(
0
)
=
1
{\displaystyle R(0)=1}
R
′
(
0
)
=
1
{\displaystyle R'(0)=1}
–ė–∑ –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č—Ö —Ä–Ķ—ą–Ķ–Ĺ–ł–Ļ —Ā–Ľ–Ķ–ī—É–Ķ—ā –≤–į–∂–Ĺ—č–Ļ –≤—č–≤–ĺ–ī –ī–Ľ—Ź —ā–Ķ–ĺ—Ä–ł–ł —Ä–į–ī–ł–ĺ—ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ö —Ü–Ķ–Ņ–Ķ–Ļ: —Ā–ł–Ĺ—É—Ā–ĺ–ł–ī–į–Ľ—Ć–Ĺ—č–Ļ —Ā–ł–≥–Ĺ–į–Ľ –Ĺ–Ķ –ł—Ā–ļ–į–∂–į–Ķ—ā —Ā–≤–ĺ—é —Ą–ĺ—Ä–ľ—É –Ņ—Ä–ł –Ņ—Ä–ĺ—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–ł –Ņ–ĺ RCL-—Ü–Ķ–Ņ—Ź–ľ, –ł—Ā–ļ–į–∂–į—é—ā—Ā—Ź —ā–ĺ–Ľ—Ć–ļ–ĺ –į–ľ–Ņ–Ľ–ł—ā—É–ī–į –ł —Ą–į–∑–į. –ü–ĺ–ī–ĺ–Ī–Ĺ—č–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–į, –Ĺ–ĺ –ĺ–Ĺ–į –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ.[–∑–Ĺ–į—á–ł–ľ–ĺ—Ā—ā—Ć —Ą–į–ļ—ā–į?
–§—É–Ĺ–ļ—Ü–ł–ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā –ł —Ā–ł–Ĺ—É—Ā –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –ļ–į–ļ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź (
f
{\displaystyle f}
g
{\displaystyle g}
—Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ [ 6]
{
f
(
x
+
y
)
=
f
(
x
)
f
(
y
)
− ‚ąí -->
g
(
x
)
g
(
y
)
g
(
x
+
y
)
=
g
(
x
)
f
(
y
)
+
f
(
x
)
g
(
y
)
{\displaystyle \left\{{\begin{array}{rcl}f(x+y)&=&f(x)f(y)-g(x)g(y)\\g(x+y)&=&g(x)f(y)+f(x)g(y)\end{array}}\right.}
–Ņ—Ä–ł –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö:
f
(
x
)
2
+
g
(
x
)
2
=
1
,
{\displaystyle f(x)^{2}+g(x)^{2}=1,}
g
(
π ŌÄ -->
/
2
)
=
1
,
{\displaystyle g(\pi /2)=1,}
0
<
g
(
x
)
<
1
{\displaystyle 0<g(x)<1}
0
<
x
<
π ŌÄ -->
/
2
{\displaystyle 0<x<\pi /2}
–ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—é –ł —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ņ—Ä–Ķ–ī–Ķ–Ľ–ĺ–≤, –ľ–ĺ–∂–Ĺ–ĺ –ī–ĺ–ļ–į–∑–į—ā—Ć, —á—ā–ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —Ā–ł–Ĺ—É—Ā–į —Ä–į–≤–Ĺ–į –ļ–ĺ—Ā–ł–Ĺ—É—Ā—É, –ł —á—ā–ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –ļ–ĺ—Ā–ł–Ĺ—É—Ā–į —Ä–į–≤–Ĺ–į –ľ–ł–Ĺ—É—Ā —Ā–ł–Ĺ—É—Ā—É. –Ę–ĺ–≥–ī–į –ľ–ĺ–∂–Ĺ–ĺ –≤–ĺ—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć—Ā—Ź —ā–Ķ–ĺ—Ä–ł–Ķ–Ļ —Ä—Ź–ī–ĺ–≤ –Ę–Ķ–Ļ–Ľ–ĺ—Ä–į –ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā—Ć —Ā–ł–Ĺ—É—Ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā –≤ –≤–ł–ī–Ķ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–Ĺ—čŐĀ—Ö —Ä—Ź–ī–ĺ–≤:
sin
‚Ā° -->
x
=
x
− ‚ąí -->
x
3
3
!
+
x
5
5
!
− ‚ąí -->
x
7
7
!
+
x
9
9
!
− ‚ąí -->
⋯ ‚čĮ -->
=
∑ ‚ąĎ -->
n
=
0
∞ ‚ąě -->
(
− ‚ąí -->
1
)
n
x
2
n
+
1
(
2
n
+
1
)
!
,
{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+{\frac {x^{9}}{9!}}-\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},}
cos
‚Ā° -->
x
=
1
− ‚ąí -->
x
2
2
!
+
x
4
4
!
− ‚ąí -->
x
6
6
!
+
x
8
8
!
− ‚ąí -->
⋯ ‚čĮ -->
=
∑ ‚ąĎ -->
n
=
0
∞ ‚ąě -->
(
− ‚ąí -->
1
)
n
x
2
n
(
2
n
)
!
.
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+{\frac {x^{8}}{8!}}-\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.}
–ü–ĺ–Ľ—Ć–∑—É—Ź—Ā—Ć —ć—ā–ł–ľ–ł —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ–ł, –į —ā–į–ļ–∂–Ķ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į–ľ–ł
tg
x
=
sin
‚Ā° -->
x
cos
‚Ā° -->
x
,
{\displaystyle \operatorname {tg} \,x={\frac {\sin x}{\cos x}},}
ctg
x
=
cos
‚Ā° -->
x
sin
‚Ā° -->
x
,
{\displaystyle \operatorname {ctg} \,x={\frac {\cos x}{\sin x}},}
sec
‚Ā° -->
x
=
1
cos
‚Ā° -->
x
{\displaystyle \sec x={\frac {1}{\cos x}}}
cosec
x
=
1
sin
‚Ā° -->
x
,
{\displaystyle \operatorname {cosec} \,x={\frac {1}{\sin x}},}
tg
x
=
x
+
1
3
x
3
+
2
15
x
5
+
17
315
x
7
+
62
2835
x
9
+
⋯ ‚čĮ -->
=
∑ ‚ąĎ -->
n
=
1
∞ ‚ąě -->
2
2
n
(
2
2
n
− ‚ąí -->
1
)
|
B
2
n
|
(
2
n
)
!
x
2
n
− ‚ąí -->
1
(
− ‚ąí -->
π ŌÄ -->
2
<
x
<
π ŌÄ -->
2
)
,
{\displaystyle {\operatorname {tg} \,x=x+{\frac {1}{3}}\,x^{3}+{\frac {2}{15}}\,x^{5}+{\frac {17}{315}}\,x^{7}+{\frac {62}{2835}}\,x^{9}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}}x^{2n-1}\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}
ctg
x
=
1
x
− ‚ąí -->
x
3
− ‚ąí -->
x
3
45
− ‚ąí -->
2
x
5
945
− ‚ąí -->
x
7
4725
− ‚ąí -->
⋯ ‚čĮ -->
=
1
x
− ‚ąí -->
∑ ‚ąĎ -->
n
=
1
∞ ‚ąě -->
2
2
n
|
B
2
n
|
(
2
n
)
!
x
2
n
− ‚ąí -->
1
(
− ‚ąí -->
π ŌÄ -->
<
x
<
π ŌÄ -->
)
,
{\displaystyle {\operatorname {ctg} \,x={\frac {1}{x}}-{\frac {x}{3}}-{\frac {x^{3}}{45}}-{\frac {2x^{5}}{945}}-{\frac {x^{7}}{4725}}-\cdots ={\frac {1}{x}}-\sum _{n=1}^{\infty }{\frac {2^{2n}|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),}}
sec
‚Ā° -->
x
=
1
+
1
2
x
2
+
5
24
x
4
+
61
720
x
6
+
277
8064
x
8
+
⋯ ‚čĮ -->
=
∑ ‚ąĎ -->
n
=
0
∞ ‚ąě -->
|
E
n
|
(
2
n
)
!
x
2
n
,
(
− ‚ąí -->
π ŌÄ -->
2
<
x
<
π ŌÄ -->
2
)
,
{\displaystyle {\sec x=1+{\frac {1}{2}}\,x^{2}+{\frac {5}{24}}\,x^{4}+{\frac {61}{720}}\,x^{6}+{\frac {277}{8064}}\,x^{8}+\cdots =\sum _{n=0}^{\infty }{\frac {|E_{n}|}{(2n)!}}\,x^{2n},\quad \left(-{\frac {\pi }{2}}<x<{\frac {\pi }{2}}\right),}}
cosec
‚Ā° -->
x
=
1
x
+
1
6
x
+
7
360
x
3
+
31
15120
x
5
+
127
604800
x
7
+
⋯ ‚čĮ -->
=
1
x
+
∑ ‚ąĎ -->
n
=
1
∞ ‚ąě -->
2
(
2
2
n
− ‚ąí -->
1
− ‚ąí -->
1
)
|
B
2
n
|
(
2
n
)
!
x
2
n
− ‚ąí -->
1
(
− ‚ąí -->
π ŌÄ -->
<
x
<
π ŌÄ -->
)
,
{\displaystyle \operatorname {cosec} x={\frac {1}{x}}+{\frac {1}{6}}\,x+{\frac {7}{360}}\,x^{3}+{\frac {31}{15120}}\,x^{5}+{\frac {127}{604800}}\,x^{7}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(2^{2n-1}-1)|B_{2n}|}{(2n)!}}\,x^{2n-1}\quad \left(-\pi <x<\pi \right),}
–≥–ī–Ķ
B
n
{\displaystyle B_{n}}
—á–ł—Ā–Ľ–į –Ď–Ķ—Ä–Ĺ—É–Ľ–Ľ–ł ,
E
n
{\displaystyle E_{n}}
—á–ł—Ā–Ľ–į –≠–Ļ–Ľ–Ķ—Ä–į .
–ó–Ĺ–į—á–Ķ–Ĺ–ł—Ź —Ā–ł–Ĺ—É—Ā–į, –ļ–ĺ—Ā–ł–Ĺ—É—Ā–į, —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į, –ļ–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į, —Ā–Ķ–ļ–į–Ĺ—Ā–į –ł –ļ–ĺ—Ā–Ķ–ļ–į–Ĺ—Ā–į –ī–Ľ—Ź –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö —É–≥–Ľ–ĺ–≤ –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ—č –≤ —ā–į–Ī–Ľ–ł—Ü–Ķ. (¬ę
∞ ‚ąě -->
{\displaystyle \infty }
—Ā—ā—Ä–Ķ–ľ–ł—ā—Ā—Ź –ļ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł ).
–ó–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ļ–ĺ—Ā–ł–Ĺ—É—Ā–į –ł —Ā–ł–Ĺ—É—Ā–į –Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł
–†–į–ī–ł–į–Ĺ—č
0
{\displaystyle 0}
π ŌÄ -->
6
{\displaystyle {\frac {\pi }{6}}}
π ŌÄ -->
4
{\displaystyle {\frac {\pi }{4}}}
π ŌÄ -->
3
{\displaystyle {\frac {\pi }{3}}}
π ŌÄ -->
2
{\displaystyle {\frac {\pi }{2}}}
π ŌÄ -->
{\displaystyle \pi }
3
π ŌÄ -->
2
{\displaystyle {\frac {3\pi }{2}}}
2
π ŌÄ -->
{\displaystyle 2\pi }
–ď—Ä–į–ī—É—Ā—č
0
∘ ‚ąė -->
{\displaystyle 0^{\circ }}
30
∘ ‚ąė -->
{\displaystyle 30^{\circ }}
45
∘ ‚ąė -->
{\displaystyle 45^{\circ }}
60
∘ ‚ąė -->
{\displaystyle 60^{\circ }}
90
∘ ‚ąė -->
{\displaystyle 90^{\circ }}
180
∘ ‚ąė -->
{\displaystyle 180^{\circ }}
270
∘ ‚ąė -->
{\displaystyle 270^{\circ }}
360
∘ ‚ąė -->
{\displaystyle 360^{\circ }}
sin
‚Ā° -->
α őĪ -->
{\displaystyle \sin \alpha }
0
{\displaystyle 0}
1
2
{\displaystyle {\frac {1}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
1
{\displaystyle 1}
0
{\displaystyle 0}
− ‚ąí -->
1
{\displaystyle -1}
0
{\displaystyle 0}
cos
‚Ā° -->
α őĪ -->
{\displaystyle \cos \alpha }
1
{\displaystyle 1}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
0
{\displaystyle 0}
− ‚ąí -->
1
{\displaystyle -1}
0
{\displaystyle 0}
1
{\displaystyle 1}
tg
α őĪ -->
{\displaystyle \operatorname {tg} \,\alpha }
0
{\displaystyle 0}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
1
{\displaystyle 1}
3
{\displaystyle {\sqrt {3}}}
∞ ‚ąě -->
{\displaystyle \infty }
0
{\displaystyle 0}
∞ ‚ąě -->
{\displaystyle \infty }
0
{\displaystyle 0}
ctg
α őĪ -->
{\displaystyle \operatorname {ctg} \,\alpha }
∞ ‚ąě -->
{\displaystyle \infty }
3
{\displaystyle {\sqrt {3}}}
1
{\displaystyle 1}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
0
{\displaystyle 0}
∞ ‚ąě -->
{\displaystyle \infty }
0
{\displaystyle 0}
∞ ‚ąě -->
{\displaystyle \infty }
sec
‚Ā° -->
α őĪ -->
{\displaystyle \sec \alpha }
1
{\displaystyle 1}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle 2}
∞ ‚ąě -->
{\displaystyle \infty }
− ‚ąí -->
1
{\displaystyle -1}
∞ ‚ąě -->
{\displaystyle \infty }
1
{\displaystyle 1}
cosec
α őĪ -->
{\displaystyle \operatorname {cosec} \,\alpha }
∞ ‚ąě -->
{\displaystyle \infty }
2
{\displaystyle 2}
2
{\displaystyle {\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
1
{\displaystyle 1}
∞ ‚ąě -->
{\displaystyle \infty }
− ‚ąí -->
1
{\displaystyle -1}
∞ ‚ąě -->
{\displaystyle \infty }
–†–į–ī–ł–į–Ĺ—č
2
π ŌÄ -->
3
{\displaystyle {\frac {2\pi }{3}}}
3
π ŌÄ -->
4
{\displaystyle {\frac {3\pi }{4}}}
5
π ŌÄ -->
6
{\displaystyle {\frac {5\pi }{6}}}
7
π ŌÄ -->
6
{\displaystyle {\frac {7\pi }{6}}}
5
π ŌÄ -->
4
{\displaystyle {\frac {5\pi }{4}}}
4
π ŌÄ -->
3
{\displaystyle {\frac {4\pi }{3}}}
5
π ŌÄ -->
3
{\displaystyle {\frac {5\pi }{3}}}
7
π ŌÄ -->
4
{\displaystyle {\frac {7\pi }{4}}}
11
π ŌÄ -->
6
{\displaystyle {\frac {11\pi }{6}}}
–ď—Ä–į–ī—É—Ā—č
120
∘ ‚ąė -->
{\displaystyle 120^{\circ }}
135
∘ ‚ąė -->
{\displaystyle 135^{\circ }}
150
∘ ‚ąė -->
{\displaystyle 150^{\circ }}
210
∘ ‚ąė -->
{\displaystyle 210^{\circ }}
225
∘ ‚ąė -->
{\displaystyle 225^{\circ }}
240
∘ ‚ąė -->
{\displaystyle 240^{\circ }}
300
∘ ‚ąė -->
{\displaystyle 300^{\circ }}
315
∘ ‚ąė -->
{\displaystyle 315^{\circ }}
330
∘ ‚ąė -->
{\displaystyle 330^{\circ }}
sin
‚Ā° -->
α őĪ -->
{\displaystyle \sin \alpha }
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
− ‚ąí -->
1
2
{\displaystyle -{\frac {1}{2}}}
− ‚ąí -->
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
− ‚ąí -->
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
− ‚ąí -->
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
− ‚ąí -->
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
− ‚ąí -->
1
2
{\displaystyle -{\frac {1}{2}}}
cos
‚Ā° -->
α őĪ -->
{\displaystyle \cos \alpha }
− ‚ąí -->
1
2
{\displaystyle -{\frac {1}{2}}}
− ‚ąí -->
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
− ‚ąí -->
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
− ‚ąí -->
3
2
{\displaystyle -{\frac {\sqrt {3}}{2}}}
− ‚ąí -->
2
2
{\displaystyle -{\frac {\sqrt {2}}{2}}}
− ‚ąí -->
1
2
{\displaystyle -{\frac {1}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
tg
α őĪ -->
{\displaystyle \operatorname {tg} \,\alpha }
− ‚ąí -->
3
{\displaystyle -{\sqrt {3}}}
− ‚ąí -->
1
{\displaystyle -1}
− ‚ąí -->
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
1
{\displaystyle 1}
3
{\displaystyle {\sqrt {3}}}
− ‚ąí -->
3
{\displaystyle -{\sqrt {3}}}
− ‚ąí -->
1
{\displaystyle -1}
− ‚ąí -->
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
ctg
α őĪ -->
{\displaystyle \operatorname {ctg} \,\alpha }
− ‚ąí -->
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
− ‚ąí -->
1
{\displaystyle -1}
− ‚ąí -->
3
{\displaystyle -{\sqrt {3}}}
3
{\displaystyle {\sqrt {3}}}
1
{\displaystyle 1}
3
3
{\displaystyle {\frac {\sqrt {3}}{3}}}
− ‚ąí -->
3
3
{\displaystyle -{\frac {\sqrt {3}}{3}}}
− ‚ąí -->
1
{\displaystyle -1}
− ‚ąí -->
3
{\displaystyle -{\sqrt {3}}}
sec
‚Ā° -->
α őĪ -->
{\displaystyle \sec \alpha }
− ‚ąí -->
2
{\displaystyle -2}
− ‚ąí -->
2
{\displaystyle -{\sqrt {2}}}
− ‚ąí -->
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
− ‚ąí -->
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
− ‚ąí -->
2
{\displaystyle -{\sqrt {2}}}
− ‚ąí -->
2
{\displaystyle -2}
2
{\displaystyle 2}
2
{\displaystyle {\sqrt {2}}}
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
cosec
α őĪ -->
{\displaystyle \operatorname {cosec} \,\alpha }
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle 2}
− ‚ąí -->
2
{\displaystyle -2}
− ‚ąí -->
2
{\displaystyle -{\sqrt {2}}}
− ‚ąí -->
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
− ‚ąí -->
2
3
3
{\displaystyle -{\frac {2{\sqrt {3}}}{3}}}
− ‚ąí -->
2
{\displaystyle -{\sqrt {2}}}
− ‚ąí -->
2
{\displaystyle -2}
–†–į–ī–ł–į–Ĺ—č
π ŌÄ -->
12
{\displaystyle {\frac {\pi }{12}}}
π ŌÄ -->
10
{\displaystyle {\frac {\pi }{10}}}
π ŌÄ -->
8
{\displaystyle {\frac {\pi }{8}}}
π ŌÄ -->
5
{\displaystyle {\frac {\pi }{5}}}
3
π ŌÄ -->
10
{\displaystyle {\frac {3\pi }{10}}}
3
π ŌÄ -->
8
{\displaystyle {\frac {3\pi }{8}}}
2
π ŌÄ -->
5
{\displaystyle {\frac {2\pi }{5}}}
5
π ŌÄ -->
12
{\displaystyle {\frac {5\pi }{12}}}
–ď—Ä–į–ī—É—Ā—č
15
∘ ‚ąė -->
{\displaystyle 15^{\circ }}
18
∘ ‚ąė -->
{\displaystyle 18^{\circ }}
22
,
5
∘ ‚ąė -->
{\displaystyle 22{,}5^{\circ }}
36
∘ ‚ąė -->
{\displaystyle 36^{\circ }}
54
∘ ‚ąė -->
{\displaystyle 54^{\circ }}
67
,
5
∘ ‚ąė -->
{\displaystyle 67{,}5^{\circ }}
72
∘ ‚ąė -->
{\displaystyle 72^{\circ }}
75
∘ ‚ąė -->
{\displaystyle 75^{\circ }}
sin
‚Ā° -->
α őĪ -->
{\displaystyle \sin \alpha }
2
− ‚ąí -->
3
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {3}}}}{2}}}
5
− ‚ąí -->
1
4
{\displaystyle {\frac {{\sqrt {5}}-1}{4}}}
2
− ‚ąí -->
2
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}
10
− ‚ąí -->
2
5
4
{\displaystyle {\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}
5
+
1
4
{\displaystyle {\frac {{\sqrt {5}}+1}{4}}}
2
+
2
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}
10
+
2
5
4
{\displaystyle {\frac {\sqrt {10+2{\sqrt {5}}}}{4}}}
2
+
3
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {3}}}}{2}}}
cos
‚Ā° -->
α őĪ -->
{\displaystyle \cos \alpha }
2
+
3
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {3}}}}{2}}}
10
+
2
5
4
{\displaystyle {\frac {\sqrt {10+2{\sqrt {5}}}}{4}}}
2
+
2
2
{\displaystyle {\frac {\sqrt {2+{\sqrt {2}}}}{2}}}
5
+
1
4
{\displaystyle {\frac {{\sqrt {5}}+1}{4}}}
10
− ‚ąí -->
2
5
4
{\displaystyle {\frac {\sqrt {10-2{\sqrt {5}}}}{4}}}
2
− ‚ąí -->
2
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {2}}}}{2}}}
5
− ‚ąí -->
1
4
{\displaystyle {\frac {{\sqrt {5}}-1}{4}}}
2
− ‚ąí -->
3
2
{\displaystyle {\frac {\sqrt {2-{\sqrt {3}}}}{2}}}
tg
α őĪ -->
{\displaystyle \operatorname {tg} \,\alpha }
2
− ‚ąí -->
3
{\displaystyle 2-{\sqrt {3}}}
25
− ‚ąí -->
10
5
5
{\displaystyle {\frac {\sqrt {25-10{\sqrt {5}}}}{5}}}
2
− ‚ąí -->
1
{\displaystyle {\sqrt {2}}-1}
5
− ‚ąí -->
2
5
{\displaystyle {\sqrt {5-2{\sqrt {5}}}}}
25
+
10
5
5
{\displaystyle {\frac {\sqrt {25+10{\sqrt {5}}}}{5}}}
2
+
1
{\displaystyle {\sqrt {2}}+1}
5
+
2
5
{\displaystyle {\sqrt {5+2{\sqrt {5}}}}}
2
+
3
{\displaystyle 2+{\sqrt {3}}}
ctg
α őĪ -->
{\displaystyle \operatorname {ctg} \,\alpha }
2
+
3
{\displaystyle 2+{\sqrt {3}}}
5
+
2
5
{\displaystyle {\sqrt {5+2{\sqrt {5}}}}}
2
+
1
{\displaystyle {\sqrt {2}}+1}
25
+
10
5
5
{\displaystyle {\frac {\sqrt {25+10{\sqrt {5}}}}{5}}}
5
− ‚ąí -->
2
5
{\displaystyle {\sqrt {5-2{\sqrt {5}}}}}
2
− ‚ąí -->
1
{\displaystyle {\sqrt {2}}-1}
25
− ‚ąí -->
10
5
5
{\displaystyle {\frac {\sqrt {25-10{\sqrt {5}}}}{5}}}
2
− ‚ąí -->
3
{\displaystyle 2-{\sqrt {3}}}
sec
‚Ā° -->
α őĪ -->
{\displaystyle \sec \alpha }
2
2
− ‚ąí -->
3
{\displaystyle 2{\sqrt {2-{\sqrt {3}}}}}
50
− ‚ąí -->
10
5
5
{\displaystyle {\frac {\sqrt {50-10{\sqrt {5}}}}{5}}}
4
− ‚ąí -->
2
2
{\displaystyle {\sqrt {4-2{\sqrt {2}}}}}
5
− ‚ąí -->
1
{\displaystyle {\sqrt {5}}-1}
50
+
10
5
5
{\displaystyle {\frac {\sqrt {50+10{\sqrt {5}}}}{5}}}
4
+
2
2
{\displaystyle {\sqrt {4+2{\sqrt {2}}}}}
5
+
1
{\displaystyle {\sqrt {5}}+1}
2
2
+
3
{\displaystyle 2{\sqrt {2+{\sqrt {3}}}}}
cosec
α őĪ -->
{\displaystyle \operatorname {cosec} \,\alpha }
2
2
+
3
{\displaystyle 2{\sqrt {2+{\sqrt {3}}}}}
5
+
1
{\displaystyle {\sqrt {5}}+1}
4
+
2
2
{\displaystyle {\sqrt {4+2{\sqrt {2}}}}}
50
+
10
5
5
{\displaystyle {\frac {\sqrt {50+10{\sqrt {5}}}}{5}}}
5
− ‚ąí -->
1
{\displaystyle {\sqrt {5}}-1}
4
− ‚ąí -->
2
2
{\displaystyle {\sqrt {4-2{\sqrt {2}}}}}
50
− ‚ąí -->
10
5
5
{\displaystyle {\frac {\sqrt {50-10{\sqrt {5}}}}{5}}}
2
2
− ‚ąí -->
3
{\displaystyle 2{\sqrt {2-{\sqrt {3}}}}}
–ó–Ĺ–į—á–Ķ–Ĺ–ł—Ź —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ī–Ľ—Ź –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö –ī—Ä—É–≥–ł—Ö —É–≥–Ľ–ĺ–≤
sin
‚Ā° -->
π ŌÄ -->
60
=
cos
‚Ā° -->
29
π ŌÄ -->
60
=
sin
‚Ā° -->
3
∘ ‚ąė -->
=
cos
‚Ā° -->
87
∘ ‚ąė -->
=
2
(
3
+
1
)
(
5
− ‚ąí -->
1
)
− ‚ąí -->
2
(
3
− ‚ąí -->
1
)
5
+
5
16
,
{\displaystyle \sin {\frac {\pi }{60}}=\cos {\frac {29\,\pi }{60}}=\sin 3^{\circ }=\cos 87^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}-1)-2({\sqrt {3}}-1){\sqrt {5+{\sqrt {5}}}}}{16}},}
cos
‚Ā° -->
π ŌÄ -->
60
=
sin
‚Ā° -->
29
π ŌÄ -->
60
=
cos
‚Ā° -->
3
∘ ‚ąė -->
=
sin
‚Ā° -->
87
∘ ‚ąė -->
=
2
(
3
− ‚ąí -->
1
)
(
5
− ‚ąí -->
1
)
+
2
(
3
+
1
)
5
+
5
16
,
{\displaystyle \cos {\frac {\pi }{60}}=\sin {\frac {29\,\pi }{60}}=\cos 3^{\circ }=\sin 87^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}-1)+2({\sqrt {3}}+1){\sqrt {5+{\sqrt {5}}}}}{16}},}
tg
‚Ā° -->
π ŌÄ -->
60
=
ctg
‚Ā° -->
29
π ŌÄ -->
60
=
tg
‚Ā° -->
3
∘ ‚ąė -->
=
ctg
‚Ā° -->
87
∘ ‚ąė -->
=
2
(
5
+
2
)
− ‚ąí -->
3
(
5
+
3
)
+
(
2
− ‚ąí -->
3
)
(
3
(
5
+
1
)
− ‚ąí -->
2
)
5
− ‚ąí -->
2
5
2
,
{\displaystyle \operatorname {tg} {\frac {\pi }{60}}=\operatorname {ctg} {\frac {29\,\pi }{60}}=\operatorname {tg} 3^{\circ }=\operatorname {ctg} 87^{\circ }={\frac {2({\sqrt {5}}+2)-{\sqrt {3}}({\sqrt {5}}+3)+(2-{\sqrt {3}})({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {5-2{\sqrt {5}}}}}{2}},}
ctg
‚Ā° -->
π ŌÄ -->
60
=
tg
‚Ā° -->
29
π ŌÄ -->
60
=
ctg
‚Ā° -->
3
∘ ‚ąė -->
=
tg
‚Ā° -->
87
∘ ‚ąė -->
=
2
(
2
(
5
+
2
)
+
3
(
5
+
3
)
)
+
(
3
(
5
− ‚ąí -->
1
)
+
2
)
2
(
25
+
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{60}}=\operatorname {tg} {\frac {29\,\pi }{60}}=\operatorname {ctg} 3^{\circ }=\operatorname {tg} 87^{\circ }={\frac {2(2({\sqrt {5}}+2)+{\sqrt {3}}({\sqrt {5}}+3))+({\sqrt {3}}({\sqrt {5}}-1)+2){\sqrt {2(25+11{\sqrt {5}})}}}{4}},}
sin
‚Ā° -->
π ŌÄ -->
30
=
cos
‚Ā° -->
7
π ŌÄ -->
15
=
sin
‚Ā° -->
6
∘ ‚ąė -->
=
cos
‚Ā° -->
84
∘ ‚ąė -->
=
6
(
5
− ‚ąí -->
5
)
− ‚ąí -->
5
− ‚ąí -->
1
8
,
{\displaystyle \sin {\frac {\pi }{30}}=\cos {\frac {7\,\pi }{15}}=\sin 6^{\circ }=\cos 84^{\circ }={\frac {{\sqrt {6(5-{\sqrt {5}})}}-{\sqrt {5}}-1}{8}},}
cos
‚Ā° -->
π ŌÄ -->
30
=
sin
‚Ā° -->
7
π ŌÄ -->
15
=
cos
‚Ā° -->
6
∘ ‚ąė -->
=
sin
‚Ā° -->
84
∘ ‚ąė -->
=
2
(
5
− ‚ąí -->
5
)
+
3
(
5
+
1
)
8
,
{\displaystyle \cos {\frac {\pi }{30}}=\sin {\frac {7\,\pi }{15}}=\cos 6^{\circ }=\sin 84^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+1)}{8}},}
tg
‚Ā° -->
π ŌÄ -->
30
=
ctg
‚Ā° -->
7
π ŌÄ -->
15
=
tg
‚Ā° -->
6
∘ ‚ąė -->
=
ctg
‚Ā° -->
84
∘ ‚ąė -->
=
2
(
5
− ‚ąí -->
5
)
− ‚ąí -->
3
(
5
− ‚ąí -->
1
)
2
,
{\displaystyle \operatorname {tg} {\frac {\pi }{30}}=\operatorname {ctg} {\frac {7\,\pi }{15}}=\operatorname {tg} 6^{\circ }=\operatorname {ctg} 84^{\circ }={\frac {{\sqrt {2(5-{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{2}},}
ctg
‚Ā° -->
π ŌÄ -->
30
=
tg
‚Ā° -->
7
π ŌÄ -->
15
=
ctg
‚Ā° -->
6
∘ ‚ąė -->
=
tg
‚Ā° -->
84
∘ ‚ąė -->
=
2
(
25
+
11
5
)
+
3
(
5
+
3
)
2
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{30}}=\operatorname {tg} {\frac {7\,\pi }{15}}=\operatorname {ctg} 6^{\circ }=\operatorname {tg} 84^{\circ }={\frac {{\sqrt {2(25+11{\sqrt {5}})}}+{\sqrt {3}}({\sqrt {5}}+3)}{2}},}
sin
‚Ā° -->
π ŌÄ -->
20
=
cos
‚Ā° -->
9
π ŌÄ -->
20
=
sin
‚Ā° -->
9
∘ ‚ąė -->
=
cos
‚Ā° -->
81
∘ ‚ąė -->
=
2
(
5
+
1
)
− ‚ąí -->
2
5
− ‚ąí -->
5
8
,
{\displaystyle \sin {\frac {\pi }{20}}=\cos {\frac {9\,\pi }{20}}=\sin 9^{\circ }=\cos 81^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)-2{\sqrt {5-{\sqrt {5}}}}}{8}},}
cos
‚Ā° -->
π ŌÄ -->
20
=
sin
‚Ā° -->
9
π ŌÄ -->
20
=
cos
‚Ā° -->
9
∘ ‚ąė -->
=
sin
‚Ā° -->
81
∘ ‚ąė -->
=
2
(
5
+
1
)
+
2
5
− ‚ąí -->
5
8
,
{\displaystyle \cos {\frac {\pi }{20}}=\sin {\frac {9\,\pi }{20}}=\cos 9^{\circ }=\sin 81^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}+1)+2{\sqrt {5-{\sqrt {5}}}}}{8}},}
tg
‚Ā° -->
π ŌÄ -->
20
=
ctg
‚Ā° -->
9
π ŌÄ -->
20
=
tg
‚Ā° -->
9
∘ ‚ąė -->
=
ctg
‚Ā° -->
81
∘ ‚ąė -->
=
5
+
1
− ‚ąí -->
5
+
2
5
,
{\displaystyle \operatorname {tg} {\frac {\pi }{20}}=\operatorname {ctg} {\frac {9\,\pi }{20}}=\operatorname {tg} 9^{\circ }=\operatorname {ctg} 81^{\circ }={{\sqrt {5}}+1-{\sqrt {5+2{\sqrt {5}}}}},}
ctg
‚Ā° -->
π ŌÄ -->
20
=
tg
‚Ā° -->
9
π ŌÄ -->
20
=
ctg
‚Ā° -->
9
∘ ‚ąė -->
=
tg
‚Ā° -->
81
∘ ‚ąė -->
=
5
+
1
+
5
+
2
5
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{20}}=\operatorname {tg} {\frac {9\,\pi }{20}}=\operatorname {ctg} 9^{\circ }=\operatorname {tg} 81^{\circ }={{\sqrt {5}}+1+{\sqrt {5+2{\sqrt {5}}}}},}
sin
‚Ā° -->
π ŌÄ -->
15
=
cos
‚Ā° -->
13
π ŌÄ -->
30
=
sin
‚Ā° -->
12
∘ ‚ąė -->
=
cos
‚Ā° -->
78
∘ ‚ąė -->
=
2
(
5
+
5
)
− ‚ąí -->
3
(
5
− ‚ąí -->
1
)
8
,
{\displaystyle \sin {\frac {\pi }{15}}=\cos {\frac {13\,\pi }{30}}=\sin 12^{\circ }=\cos 78^{\circ }={\frac {{\sqrt {2(5+{\sqrt {5}})}}-{\sqrt {3}}({\sqrt {5}}-1)}{8}},}
cos
‚Ā° -->
π ŌÄ -->
15
=
sin
‚Ā° -->
13
π ŌÄ -->
30
=
cos
‚Ā° -->
12
∘ ‚ąė -->
=
sin
‚Ā° -->
78
∘ ‚ąė -->
=
6
(
5
+
5
)
+
5
− ‚ąí -->
1
8
,
{\displaystyle \cos {\frac {\pi }{15}}=\sin {\frac {13\,\pi }{30}}=\cos 12^{\circ }=\sin 78^{\circ }={\frac {{\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1}{8}},}
tg
‚Ā° -->
π ŌÄ -->
15
=
ctg
‚Ā° -->
13
π ŌÄ -->
30
=
tg
‚Ā° -->
12
∘ ‚ąė -->
=
ctg
‚Ā° -->
78
∘ ‚ąė -->
=
3
(
3
− ‚ąí -->
5
)
− ‚ąí -->
2
(
25
− ‚ąí -->
11
5
)
2
,
{\displaystyle \operatorname {tg} {\frac {\pi }{15}}=\operatorname {ctg} {\frac {13\,\pi }{30}}=\operatorname {tg} 12^{\circ }=\operatorname {ctg} 78^{\circ }={\frac {{\sqrt {3}}(3-{\sqrt {5}})-{\sqrt {2(25-11{\sqrt {5}})}}}{2}},}
ctg
‚Ā° -->
π ŌÄ -->
15
=
tg
‚Ā° -->
13
π ŌÄ -->
30
=
ctg
‚Ā° -->
12
∘ ‚ąė -->
=
tg
‚Ā° -->
78
∘ ‚ąė -->
=
3
(
5
+
1
)
+
2
(
5
+
5
)
2
,
{\displaystyle \operatorname {ctg} {\frac {\pi }{15}}=\operatorname {tg} {\frac {13\,\pi }{30}}=\operatorname {ctg} 12^{\circ }=\operatorname {tg} 78^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)+{\sqrt {2(5+{\sqrt {5}})}}}{2}},}
sin
‚Ā° -->
7
π ŌÄ -->
60
=
cos
‚Ā° -->
23
π ŌÄ -->
60
=
sin
‚Ā° -->
21
∘ ‚ąė -->
=
cos
‚Ā° -->
69
∘ ‚ąė -->
=
− ‚ąí -->
2
(
3
− ‚ąí -->
1
)
(
5
+
1
)
+
2
(
3
+
1
)
5
− ‚ąí -->
5
16
,
{\displaystyle \sin {\frac {7\,\pi }{60}}=\cos {\frac {23\,\pi }{60}}=\sin 21^{\circ }=\cos 69^{\circ }={\frac {-{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}+1)+2({\sqrt {3}}+1){\sqrt {5-{\sqrt {5}}}}}{16}},}
cos
‚Ā° -->
7
π ŌÄ -->
60
=
sin
‚Ā° -->
23
π ŌÄ -->
60
=
cos
‚Ā° -->
21
∘ ‚ąė -->
=
sin
‚Ā° -->
69
∘ ‚ąė -->
=
2
(
3
+
1
)
(
5
+
1
)
+
2
(
3
− ‚ąí -->
1
)
5
− ‚ąí -->
5
16
,
{\displaystyle \cos {\frac {7\,\pi }{60}}=\sin {\frac {23\,\pi }{60}}=\cos 21^{\circ }=\sin 69^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}+1)+2({\sqrt {3}}-1){\sqrt {5-{\sqrt {5}}}}}{16}},}
tg
‚Ā° -->
7
π ŌÄ -->
60
=
ctg
‚Ā° -->
23
π ŌÄ -->
60
=
tg
‚Ā° -->
21
∘ ‚ąė -->
=
ctg
‚Ā° -->
69
∘ ‚ąė -->
=
2
(
2
(
5
− ‚ąí -->
2
)
− ‚ąí -->
3
(
3
− ‚ąí -->
5
)
)
+
(
3
(
5
+
1
)
− ‚ąí -->
2
)
2
(
25
− ‚ąí -->
11
5
)
4
,
{\displaystyle \operatorname {tg} {\frac {7\,\pi }{60}}=\operatorname {ctg} {\frac {23\,\pi }{60}}=\operatorname {tg} 21^{\circ }=\operatorname {ctg} 69^{\circ }={\frac {2(2({\sqrt {5}}-2)-{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
ctg
‚Ā° -->
7
π ŌÄ -->
60
=
tg
‚Ā° -->
23
π ŌÄ -->
60
=
ctg
‚Ā° -->
21
∘ ‚ąė -->
=
tg
‚Ā° -->
69
∘ ‚ąė -->
=
2
(
2
(
5
− ‚ąí -->
2
)
+
3
(
3
− ‚ąí -->
5
)
)
+
(
3
(
5
+
1
)
+
2
)
2
(
25
− ‚ąí -->
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {7\,\pi }{60}}=\operatorname {tg} {\frac {23\,\pi }{60}}=\operatorname {ctg} 21^{\circ }=\operatorname {tg} 69^{\circ }={\frac {2(2({\sqrt {5}}-2)+{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)+2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
sin
‚Ā° -->
2
π ŌÄ -->
15
=
cos
‚Ā° -->
11
π ŌÄ -->
30
=
sin
‚Ā° -->
24
∘ ‚ąė -->
=
cos
‚Ā° -->
66
∘ ‚ąė -->
=
3
(
5
+
1
)
− ‚ąí -->
2
(
5
− ‚ąí -->
5
)
8
,
{\displaystyle \sin {\frac {2\,\pi }{15}}=\cos {\frac {11\,\pi }{30}}=\sin 24^{\circ }=\cos 66^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2(5-{\sqrt {5}})}}}{8}},}
cos
‚Ā° -->
2
π ŌÄ -->
15
=
sin
‚Ā° -->
11
π ŌÄ -->
30
=
cos
‚Ā° -->
24
∘ ‚ąė -->
=
sin
‚Ā° -->
66
∘ ‚ąė -->
=
5
+
1
+
6
(
5
− ‚ąí -->
5
)
8
,
{\displaystyle \cos {\frac {2\,\pi }{15}}=\sin {\frac {11\,\pi }{30}}=\cos 24^{\circ }=\sin 66^{\circ }={\frac {{\sqrt {5}}+1+{\sqrt {6(5-{\sqrt {5}})}}}{8}},}
tg
‚Ā° -->
2
π ŌÄ -->
15
=
ctg
‚Ā° -->
11
π ŌÄ -->
30
=
tg
‚Ā° -->
24
∘ ‚ąė -->
=
ctg
‚Ā° -->
66
∘ ‚ąė -->
=
− ‚ąí -->
3
(
3
+
5
)
+
2
(
25
+
11
5
)
2
,
{\displaystyle \operatorname {tg} {\frac {2\,\pi }{15}}=\operatorname {ctg} {\frac {11\,\pi }{30}}=\operatorname {tg} 24^{\circ }=\operatorname {ctg} 66^{\circ }={\frac {-{\sqrt {3}}(3+{\sqrt {5}})+{\sqrt {2(25+11{\sqrt {5}})}}}{2}},}
ctg
‚Ā° -->
2
π ŌÄ -->
15
=
tg
‚Ā° -->
11
π ŌÄ -->
30
=
ctg
‚Ā° -->
24
∘ ‚ąė -->
=
tg
‚Ā° -->
66
∘ ‚ąė -->
=
3
(
5
− ‚ąí -->
1
)
+
2
(
5
− ‚ąí -->
5
)
2
,
{\displaystyle \operatorname {ctg} {\frac {2\,\pi }{15}}=\operatorname {tg} {\frac {11\,\pi }{30}}=\operatorname {ctg} 24^{\circ }=\operatorname {tg} 66^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}-1)+{\sqrt {2(5-{\sqrt {5}})}}}{2}},}
sin
‚Ā° -->
3
π ŌÄ -->
20
=
cos
‚Ā° -->
7
π ŌÄ -->
20
=
sin
‚Ā° -->
27
∘ ‚ąė -->
=
cos
‚Ā° -->
63
∘ ‚ąė -->
=
− ‚ąí -->
2
(
5
− ‚ąí -->
1
)
+
2
5
+
5
8
,
{\displaystyle \sin {\frac {3\,\pi }{20}}=\cos {\frac {7\,\pi }{20}}=\sin 27^{\circ }=\cos 63^{\circ }={\frac {-{\sqrt {2}}({\sqrt {5}}-1)+2{\sqrt {5+{\sqrt {5}}}}}{8}},}
cos
‚Ā° -->
3
π ŌÄ -->
20
=
sin
‚Ā° -->
7
π ŌÄ -->
20
=
cos
‚Ā° -->
27
∘ ‚ąė -->
=
sin
‚Ā° -->
63
∘ ‚ąė -->
=
2
(
5
− ‚ąí -->
1
)
+
2
5
+
5
8
,
{\displaystyle \cos {\frac {3\,\pi }{20}}=\sin {\frac {7\,\pi }{20}}=\cos 27^{\circ }=\sin 63^{\circ }={\frac {{\sqrt {2}}({\sqrt {5}}-1)+2{\sqrt {5+{\sqrt {5}}}}}{8}},}
tg
‚Ā° -->
3
π ŌÄ -->
20
=
ctg
‚Ā° -->
7
π ŌÄ -->
20
=
tg
‚Ā° -->
27
∘ ‚ąė -->
=
ctg
‚Ā° -->
63
∘ ‚ąė -->
=
5
− ‚ąí -->
1
− ‚ąí -->
5
− ‚ąí -->
2
5
,
{\displaystyle \operatorname {tg} {\frac {3\,\pi }{20}}=\operatorname {ctg} {\frac {7\,\pi }{20}}=\operatorname {tg} 27^{\circ }=\operatorname {ctg} 63^{\circ }={{\sqrt {5}}-1-{\sqrt {5-2{\sqrt {5}}}}},}
ctg
‚Ā° -->
3
π ŌÄ -->
20
=
tg
‚Ā° -->
7
π ŌÄ -->
20
=
ctg
‚Ā° -->
27
∘ ‚ąė -->
=
tg
‚Ā° -->
63
∘ ‚ąė -->
=
5
− ‚ąí -->
1
+
5
− ‚ąí -->
2
5
,
{\displaystyle \operatorname {ctg} {\frac {3\,\pi }{20}}=\operatorname {tg} {\frac {7\,\pi }{20}}=\operatorname {ctg} 27^{\circ }=\operatorname {tg} 63^{\circ }={{\sqrt {5}}-1+{\sqrt {5-2{\sqrt {5}}}}},}
sin
‚Ā° -->
11
π ŌÄ -->
60
=
cos
‚Ā° -->
19
π ŌÄ -->
60
=
sin
‚Ā° -->
33
∘ ‚ąė -->
=
cos
‚Ā° -->
57
∘ ‚ąė -->
=
2
(
3
+
1
)
(
5
− ‚ąí -->
1
)
+
2
(
3
− ‚ąí -->
1
)
5
+
5
16
,
{\displaystyle \sin {\frac {11\,\pi }{60}}=\cos {\frac {19\,\pi }{60}}=\sin 33^{\circ }=\cos 57^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}-1)+2({\sqrt {3}}-1){\sqrt {5+{\sqrt {5}}}}}{16}},}
cos
‚Ā° -->
11
π ŌÄ -->
60
=
sin
‚Ā° -->
19
π ŌÄ -->
60
=
cos
‚Ā° -->
33
∘ ‚ąė -->
=
sin
‚Ā° -->
57
∘ ‚ąė -->
=
− ‚ąí -->
2
(
3
− ‚ąí -->
1
)
(
5
− ‚ąí -->
1
)
+
2
(
3
+
1
)
5
+
5
16
,
{\displaystyle \cos {\frac {11\,\pi }{60}}=\sin {\frac {19\,\pi }{60}}=\cos 33^{\circ }=\sin 57^{\circ }={\frac {-{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}-1)+2({\sqrt {3}}+1){\sqrt {5+{\sqrt {5}}}}}{16}},}
tg
‚Ā° -->
11
π ŌÄ -->
60
=
ctg
‚Ā° -->
19
π ŌÄ -->
60
=
tg
‚Ā° -->
33
∘ ‚ąė -->
=
ctg
‚Ā° -->
57
∘ ‚ąė -->
=
− ‚ąí -->
2
(
5
+
2
)
+
3
(
3
+
5
)
+
(
2
− ‚ąí -->
3
)
(
3
(
5
+
1
)
− ‚ąí -->
2
)
5
− ‚ąí -->
2
5
2
,
{\displaystyle \operatorname {tg} {\frac {11\,\pi }{60}}=\operatorname {ctg} {\frac {19\,\pi }{60}}=\operatorname {tg} 33^{\circ }=\operatorname {ctg} 57^{\circ }={\frac {-2({\sqrt {5}}+2)+{\sqrt {3}}(3+{\sqrt {5}})+(2-{\sqrt {3}})({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {5-2{\sqrt {5}}}}}{2}},}
ctg
‚Ā° -->
11
π ŌÄ -->
60
=
tg
‚Ā° -->
19
π ŌÄ -->
60
=
ctg
‚Ā° -->
33
∘ ‚ąė -->
=
tg
‚Ā° -->
57
∘ ‚ąė -->
=
− ‚ąí -->
2
(
2
(
5
+
2
)
+
3
(
3
+
5
)
)
+
(
3
(
5
− ‚ąí -->
1
)
+
2
)
2
(
25
+
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {11\,\pi }{60}}=\operatorname {tg} {\frac {19\,\pi }{60}}=\operatorname {ctg} 33^{\circ }=\operatorname {tg} 57^{\circ }={\frac {-2(2({\sqrt {5}}+2)+{\sqrt {3}}(3+{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}-1)+2){\sqrt {2(25+11{\sqrt {5}})}}}{4}},}
sin
‚Ā° -->
13
π ŌÄ -->
60
=
cos
‚Ā° -->
17
π ŌÄ -->
60
=
sin
‚Ā° -->
39
∘ ‚ąė -->
=
cos
‚Ā° -->
51
∘ ‚ąė -->
=
2
(
3
+
1
)
(
5
+
1
)
− ‚ąí -->
2
(
3
− ‚ąí -->
1
)
5
− ‚ąí -->
5
16
,
{\displaystyle \sin {\frac {13\,\pi }{60}}=\cos {\frac {17\,\pi }{60}}=\sin 39^{\circ }=\cos 51^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}+1)({\sqrt {5}}+1)-2({\sqrt {3}}-1){\sqrt {5-{\sqrt {5}}}}}{16}},}
cos
‚Ā° -->
13
π ŌÄ -->
60
=
sin
‚Ā° -->
17
π ŌÄ -->
60
=
cos
‚Ā° -->
39
∘ ‚ąė -->
=
sin
‚Ā° -->
51
∘ ‚ąė -->
=
2
(
3
− ‚ąí -->
1
)
(
5
+
1
)
+
2
(
3
+
1
)
5
− ‚ąí -->
5
16
,
{\displaystyle \cos {\frac {13\,\pi }{60}}=\sin {\frac {17\,\pi }{60}}=\cos 39^{\circ }=\sin 51^{\circ }={\frac {{\sqrt {2}}({\sqrt {3}}-1)({\sqrt {5}}+1)+2({\sqrt {3}}+1){\sqrt {5-{\sqrt {5}}}}}{16}},}
tg
‚Ā° -->
13
π ŌÄ -->
60
=
ctg
‚Ā° -->
17
π ŌÄ -->
60
=
tg
‚Ā° -->
39
∘ ‚ąė -->
=
ctg
‚Ā° -->
51
∘ ‚ąė -->
=
− ‚ąí -->
2
(
2
(
5
− ‚ąí -->
2
)
+
3
(
3
− ‚ąí -->
5
)
)
+
(
3
(
5
+
1
)
+
2
)
2
(
25
− ‚ąí -->
11
5
)
4
,
{\displaystyle \operatorname {tg} {\frac {13\,\pi }{60}}=\operatorname {ctg} {\frac {17\,\pi }{60}}=\operatorname {tg} 39^{\circ }=\operatorname {ctg} 51^{\circ }={\frac {-2(2({\sqrt {5}}-2)+{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)+2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
ctg
‚Ā° -->
13
π ŌÄ -->
60
=
tg
‚Ā° -->
17
π ŌÄ -->
60
=
ctg
‚Ā° -->
39
∘ ‚ąė -->
=
tg
‚Ā° -->
51
∘ ‚ąė -->
=
− ‚ąí -->
2
(
2
(
5
− ‚ąí -->
2
)
− ‚ąí -->
3
(
3
− ‚ąí -->
5
)
)
+
(
3
(
5
+
1
)
− ‚ąí -->
2
)
2
(
25
− ‚ąí -->
11
5
)
4
,
{\displaystyle \operatorname {ctg} {\frac {13\,\pi }{60}}=\operatorname {tg} {\frac {17\,\pi }{60}}=\operatorname {ctg} 39^{\circ }=\operatorname {tg} 51^{\circ }={\frac {-2(2({\sqrt {5}}-2)-{\sqrt {3}}(3-{\sqrt {5}}))+({\sqrt {3}}({\sqrt {5}}+1)-2){\sqrt {2(25-11{\sqrt {5}})}}}{4}},}
sin
‚Ā° -->
7
π ŌÄ -->
30
=
cos
‚Ā° -->
8
π ŌÄ -->
30
=
sin
‚Ā° -->
42
∘ ‚ąė -->
=
cos
‚Ā° -->
48
∘ ‚ąė -->
=
− ‚ąí -->
(
5
− ‚ąí -->
1
)
+
6
(
5
+
5
)
8
,
{\displaystyle \sin {\frac {7\,\pi }{30}}=\cos {\frac {8\,\pi }{30}}=\sin 42^{\circ }=\cos 48^{\circ }={\frac {-({\sqrt {5}}-1)+{\sqrt {6(5+{\sqrt {5}})}}}{8}},}
cos
‚Ā° -->
7
π ŌÄ -->
30
=
sin
‚Ā° -->
8
π ŌÄ -->
30
=
cos
‚Ā° -->
42
∘ ‚ąė -->
=
sin
‚Ā° -->
48
∘ ‚ąė -->
=
3
(
5
− ‚ąí -->
1
)
+
2
(
5
+
5
)
8
,
{\displaystyle \cos {\frac {7\,\pi }{30}}=\sin {\frac {8\,\pi }{30}}=\cos 42^{\circ }=\sin 48^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}-1)+{\sqrt {2(5+{\sqrt {5}})}}}{8}},}
tg
‚Ā° -->
7
π ŌÄ -->
30
=
ctg
‚Ā° -->
8
π ŌÄ -->
30
=
tg
‚Ā° -->
42
∘ ‚ąė -->
=
ctg
‚Ā° -->
48
∘ ‚ąė -->
=
3
(
5
+
1
)
− ‚ąí -->
2
(
5
+
5
)
2
,
{\displaystyle \operatorname {tg} {\frac {7\,\pi }{30}}=\operatorname {ctg} {\frac {8\,\pi }{30}}=\operatorname {tg} 42^{\circ }=\operatorname {ctg} 48^{\circ }={\frac {{\sqrt {3}}({\sqrt {5}}+1)-{\sqrt {2(5+{\sqrt {5}})}}}{2}},}
ctg
‚Ā° -->
7
π ŌÄ -->
30
=
tg
‚Ā° -->
8
π ŌÄ -->
30
=
ctg
‚Ā° -->
42
∘ ‚ąė -->
=
tg
‚Ā° -->
48
∘ ‚ąė -->
=
3
(
3
− ‚ąí -->
5
)
+
2
(
25
− ‚ąí -->
11
5
)
2
,
{\displaystyle \operatorname {ctg} {\frac {7\,\pi }{30}}=\operatorname {tg} {\frac {8\,\pi }{30}}=\operatorname {ctg} 42^{\circ }=\operatorname {tg} 48^{\circ }={\frac {{\sqrt {3}}(3-{\sqrt {5}})+{\sqrt {2(25-11{\sqrt {5}})}}}{2}},}
tg
‚Ā° -->
π ŌÄ -->
120
=
ctg
‚Ā° -->
59
π ŌÄ -->
120
=
tg
‚Ā° -->
1.5
∘ ‚ąė -->
=
ctg
‚Ā° -->
88.5
∘ ‚ąė -->
=
8
− ‚ąí -->
2
(
2
− ‚ąí -->
3
)
(
3
− ‚ąí -->
5
)
− ‚ąí -->
2
(
2
+
3
)
(
5
+
5
)
8
+
2
(
2
− ‚ąí -->
3
)
(
3
− ‚ąí -->
5
)
+
2
(
2
+
3
)
(
5
+
5
)
,
{\displaystyle \operatorname {tg} {\frac {\pi }{120}}=\operatorname {ctg} {\frac {59\,\pi }{120}}=\operatorname {tg} 1.5^{\circ }=\operatorname {ctg} 88.5^{\circ }={\sqrt {\frac {8-{\sqrt {2(2-{\sqrt {3}})(3-{\sqrt {5}})}}-{\sqrt {2(2+{\sqrt {3}})(5+{\sqrt {5}})}}}{8+{\sqrt {2(2-{\sqrt {3}})(3-{\sqrt {5}})}}+{\sqrt {2(2+{\sqrt {3}})(5+{\sqrt {5}})}}}}},}
cos
‚Ā° -->
π ŌÄ -->
240
=
sin
‚Ā° -->
119
π ŌÄ -->
240
=
cos
‚Ā° -->
0.75
∘ ‚ąė -->
=
sin
‚Ā° -->
89.25
∘ ‚ąė -->
=
1
16
(
2
− ‚ąí -->
2
+
2
(
2
(
5
+
5
)
+
3
(
1
− ‚ąí -->
5
)
)
+
2
+
2
+
2
(
6
(
5
+
5
)
+
5
− ‚ąí -->
1
)
)
,
{\displaystyle \cos {\frac {\pi }{240}}=\sin {\frac {119\,\pi }{240}}=\cos 0.75^{\circ }=\sin 89.25^{\circ }={\frac {1}{16}}\left({\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}\left({\sqrt {2(5+{\sqrt {5}})}}+{\sqrt {3}}(1-{\sqrt {5}})\right)+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}\left({\sqrt {6(5+{\sqrt {5}})}}+{\sqrt {5}}-1\right)\right),}
cos
‚Ā° -->
π ŌÄ -->
17
=
sin
‚Ā° -->
15
π ŌÄ -->
34
=
1
8
2
(
2
3
17
− ‚ąí -->
2
(
85
+
19
17
)
+
17
+
2
(
17
− ‚ąí -->
17
)
+
17
+
15
)
.
{\displaystyle \cos {\frac {\pi }{17}}=\sin {\frac {15\,\pi }{34}}={\frac {1}{8}}{\sqrt {2\left(2{\sqrt {3{\sqrt {17}}-{\sqrt {2(85+19{\sqrt {17}})}}+17}}+{\sqrt {2(17-{\sqrt {17}})}}+{\sqrt {17}}+15\right)}}.}
sin
‚Ā° -->
π ŌÄ -->
2
n
+
1
=
1
2
2
− ‚ąí -->
2
+
⋯ ‚čĮ -->
+
2
⏟ ‚Źü -->
n
,
n
∈ ‚ąą -->
N
{\displaystyle \sin {\pi \over 2^{n+1}}={1 \over 2}\underbrace {\sqrt {2-{\sqrt {2+\dots +{\sqrt {2}}}}}} _{n},n\in \mathbb {N} }
cos
‚Ā° -->
π ŌÄ -->
2
n
+
1
=
1
2
2
+
2
+
⋯ ‚čĮ -->
+
2
⏟ ‚Źü -->
n
,
n
∈ ‚ąą -->
N
{\displaystyle \cos {\pi \over 2^{n+1}}={1 \over 2}\underbrace {\sqrt {2+{\sqrt {2+\dots +{\sqrt {2}}}}}} _{n},n\in \mathbb {N} }
sin
‚Ā° -->
π ŌÄ -->
3
⋅ ‚čÖ -->
2
n
=
1
2
2
− ‚ąí -->
2
+
⋯ ‚čĮ -->
+
3
⏟ ‚Źü -->
n
,
n
≥ ‚Č• -->
2
{\displaystyle \sin {\pi \over 3\cdot 2^{n}}={1 \over 2}\underbrace {\sqrt {2-{\sqrt {2+\dots +{\sqrt {3}}}}}} _{n},n\geq 2}
cos
‚Ā° -->
π ŌÄ -->
3
⋅ ‚čÖ -->
2
n
=
1
2
2
+
2
+
⋯ ‚čĮ -->
+
3
⏟ ‚Źü -->
n
,
n
≥ ‚Č• -->
2
{\displaystyle \cos {\pi \over 3\cdot 2^{n}}={1 \over 2}\underbrace {\sqrt {2+{\sqrt {2+\dots +{\sqrt {3}}}}}} _{n},n\geq 2}
–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —Ā–ł–Ĺ—É—Ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ĺ—Ä–ī–ł–Ĺ–į—ā–ĺ–Ļ –ł –į–Ī—Ā—Ü–ł—Ā—Ā–ĺ–Ļ —ā–ĺ—á–ļ–ł, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ –Ĺ–į –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —É–≥–Ľ—É őĪ , —ā–ĺ —Ā–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł (
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
—ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ü–ł—Ą–į–≥–ĺ—Ä–į –ł–ľ–Ķ–Ķ–ľ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ
α őĪ -->
{\displaystyle \alpha }
sin
2
‚Ā° -->
α őĪ -->
+
cos
2
‚Ā° -->
α őĪ -->
=
1.
{\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1.}
–≠—ā–ĺ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č–ľ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–ľ —ā–ĺ–∂–ī–Ķ—Ā—ā–≤–ĺ–ľ
–†–į–∑–ī–Ķ–Ľ–ł–≤ —ć—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā –ļ–ĺ—Ā–ł–Ĺ—É—Ā–į –ł —Ā–ł–Ĺ—É—Ā–į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –Ņ–ĺ–Ľ—É—á–ł–ľ:
1
+
t
g
2
α őĪ -->
=
s
e
c
2
α őĪ -->
,
{\displaystyle 1+\mathop {\mathrm {tg} } \,^{2}\alpha =\mathop {\mathrm {sec} } \,^{2}\alpha ,}
1
+
c
t
g
2
α őĪ -->
=
c
o
s
e
c
2
α őĪ -->
.
{\displaystyle 1+\mathop {\mathrm {ctg} } \,^{2}\alpha =\mathop {\mathrm {cosec} } \,^{2}\alpha .}
–ė–∑ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į –ł –ļ–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ
t
g
α őĪ -->
⋅ ‚čÖ -->
c
t
g
α őĪ -->
=
1.
{\displaystyle \mathop {\mathrm {tg} } \,\alpha \cdot \mathop {\mathrm {ctg} } \,\alpha =1.}
–õ—é–Ī—É—é —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ—É—é —Ą—É–Ĺ–ļ—Ü–ł—é –ľ–ĺ–∂–Ĺ–ĺ –≤—č—Ä–į–∑–ł—ā—Ć —á–Ķ—Ä–Ķ–∑ –Ľ—é–Ī—É—é –ī—Ä—É–≥—É—é —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ—É—é —Ą—É–Ĺ–ļ—Ü–ł—é —Ā —ā–Ķ–ľ –∂–Ķ –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–ľ (—Ā —ā–ĺ—á–Ĺ–ĺ—Ā—ā—Ć—é –ī–ĺ –∑–Ĺ–į–ļ–į –ł–∑-–∑–į –Ĺ–Ķ–ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ—Ā—ā–ł —Ä–į—Ā–ļ—Ä—č—ā–ł—Ź –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –ļ–ĺ—Ä–Ĺ—Ź). –Ě–ł–∂–Ķ–Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –≤–Ķ—Ä–Ĺ—č –ī–Ľ—Ź
0
<
x
<
π ŌÄ -->
/
2
{\displaystyle 0<x<\pi /2}
sin
cos
tg
ctg
sec
cosec
sin
‚Ā° -->
x
=
{\displaystyle \,\sin x=}
sin
‚Ā° -->
x
{\displaystyle \,\sin x}
1
− ‚ąí -->
cos
2
‚Ā° -->
x
{\displaystyle {\sqrt {1-\cos ^{2}x}}}
tg
‚Ā° -->
x
1
+
tg
2
‚Ā° -->
x
{\displaystyle {\frac {\operatorname {tg} x}{\sqrt {1+\operatorname {tg} ^{2}x}}}}
1
ctg
2
‚Ā° -->
x
+
1
{\displaystyle {\frac {1}{\sqrt {\operatorname {ctg} ^{2}x+1}}}}
sec
2
‚Ā° -->
x
− ‚ąí -->
1
sec
‚Ā° -->
x
{\displaystyle {\frac {\sqrt {\sec ^{2}x-1}}{\sec x}}}
1
cosec
‚Ā° -->
x
{\displaystyle {\frac {1}{\operatorname {cosec} x}}}
cos
‚Ā° -->
x
=
{\displaystyle \,\cos x=}
1
− ‚ąí -->
sin
2
‚Ā° -->
x
{\displaystyle \,{\sqrt {1-\sin ^{2}x}}}
cos
‚Ā° -->
x
{\displaystyle \,\cos x}
1
1
+
tg
2
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\sqrt {1+\operatorname {tg} ^{2}x}}}}
ctg
‚Ā° -->
x
ctg
2
‚Ā° -->
x
+
1
{\displaystyle \,{\frac {\operatorname {ctg} x}{\sqrt {\operatorname {ctg} ^{2}x+1}}}}
1
sec
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\sec x}}}
cosec
2
‚Ā° -->
x
− ‚ąí -->
1
cosec
‚Ā° -->
x
{\displaystyle \,{\frac {\sqrt {\operatorname {cosec} ^{2}x-1}}{\operatorname {cosec} x}}}
tg
‚Ā° -->
x
=
{\displaystyle \,\operatorname {tg} x=}
sin
‚Ā° -->
x
1
− ‚ąí -->
sin
2
‚Ā° -->
x
{\displaystyle \,{\frac {\sin x}{\sqrt {1-\sin ^{2}x}}}}
1
− ‚ąí -->
cos
2
‚Ā° -->
x
cos
‚Ā° -->
x
{\displaystyle \,{\frac {\sqrt {1-\cos ^{2}x}}{\cos x}}}
tg
‚Ā° -->
x
{\displaystyle \,\operatorname {tg} x}
1
ctg
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\operatorname {ctg} x}}}
sec
2
‚Ā° -->
x
− ‚ąí -->
1
{\displaystyle \,{\sqrt {\sec ^{2}x-1}}}
1
cosec
2
‚Ā° -->
x
− ‚ąí -->
1
{\displaystyle \,{\frac {1}{\sqrt {\operatorname {cosec} ^{2}x-1}}}}
ctg
‚Ā° -->
x
=
{\displaystyle \,\operatorname {ctg} x=}
1
− ‚ąí -->
sin
2
‚Ā° -->
x
sin
‚Ā° -->
x
{\displaystyle \,{\frac {\sqrt {1-\sin ^{2}x}}{\sin x}}}
cos
‚Ā° -->
x
1
− ‚ąí -->
cos
2
‚Ā° -->
x
{\displaystyle \,{\frac {\cos x}{\sqrt {1-\cos ^{2}x}}}}
1
tg
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\operatorname {tg} x}}}
ctg
‚Ā° -->
x
{\displaystyle \,\operatorname {ctg} x}
1
sec
2
‚Ā° -->
x
− ‚ąí -->
1
{\displaystyle \,{\frac {1}{\sqrt {\sec ^{2}x-1}}}}
cosec
2
‚Ā° -->
x
− ‚ąí -->
1
{\displaystyle \,{\sqrt {\operatorname {cosec} ^{2}x-1}}}
sec
‚Ā° -->
x
=
{\displaystyle \,\sec x=}
1
1
− ‚ąí -->
sin
2
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\sqrt {1-\sin ^{2}x}}}}
1
cos
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\cos x}}}
1
+
tg
2
‚Ā° -->
x
{\displaystyle \,{\sqrt {1+\operatorname {tg} ^{2}x}}}
ctg
2
‚Ā° -->
x
+
1
ctg
‚Ā° -->
x
{\displaystyle \,{\frac {\sqrt {\operatorname {ctg} ^{2}x+1}}{\operatorname {ctg} x}}}
sec
‚Ā° -->
x
{\displaystyle \,\sec x}
cosec
‚Ā° -->
x
cosec
2
‚Ā° -->
x
− ‚ąí -->
1
{\displaystyle \,{\frac {\operatorname {cosec} x}{\sqrt {\operatorname {cosec} ^{2}x-1}}}}
cosec
‚Ā° -->
x
=
{\displaystyle \,\operatorname {cosec} x=}
1
sin
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\sin x}}}
1
1
− ‚ąí -->
cos
2
‚Ā° -->
x
{\displaystyle \,{\frac {1}{\sqrt {1-\cos ^{2}x}}}}
1
+
tg
2
‚Ā° -->
x
tg
‚Ā° -->
x
{\displaystyle \,{\frac {\sqrt {1+\operatorname {tg} ^{2}x}}{\operatorname {tg} x}}}
ctg
2
‚Ā° -->
x
+
1
{\displaystyle \,{\sqrt {\operatorname {ctg} ^{2}x+1}}}
sec
‚Ā° -->
x
sec
2
‚Ā° -->
x
− ‚ąí -->
1
{\displaystyle \,{\frac {\sec x}{\sqrt {\sec ^{2}x-1}}}}
cosec
‚Ā° -->
x
{\displaystyle \,\operatorname {cosec} x}
–°–ł–Ĺ—É—Ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā ‚ÄĒ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł .
–Ę–į–Ĺ–≥–Ķ–Ĺ—Ā –ł —Ā–Ķ–ļ–į–Ĺ—Ā –ł–ľ–Ķ—é—ā —ā–ĺ—á–ļ–ł —Ä–į–∑—Ä—č–≤–į
π ŌÄ -->
/
2
+
π ŌÄ -->
k
{\displaystyle \pi /2+\pi k}
k
{\displaystyle k}
—Ü–Ķ–Ľ–ĺ–Ķ .
–ö–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā –ł –ļ–ĺ—Ā–Ķ–ļ–į–Ĺ—Ā –ł–ľ–Ķ—é—ā —ā–ĺ—á–ļ–ł —Ä–į–∑—Ä—č–≤–į
π ŌÄ -->
k
{\displaystyle \pi k}
k
{\displaystyle k}
—Ü–Ķ–Ľ–ĺ–Ķ .
–ö–ĺ—Ā–ł–Ĺ—É—Ā –ł —Ā–Ķ–ļ–į–Ĺ—Ā ‚ÄĒ —á—Ď—ā–Ĺ—č–Ķ . –ě—Ā—ā–į–Ľ—Ć–Ĺ—č–Ķ —á–Ķ—ā—č—Ä–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł ‚ÄĒ –Ĺ–Ķ—á—Ď—ā–Ĺ—č–Ķ , —ā–ĺ –Ķ—Ā—ā—Ć:
sin
‚Ā° -->
(
− ‚ąí -->
α őĪ -->
)
=
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
,
{\displaystyle \sin \left(-\alpha \right)=-\sin \alpha \,,}
cos
‚Ā° -->
(
− ‚ąí -->
α őĪ -->
)
=
cos
‚Ā° -->
α őĪ -->
,
{\displaystyle \cos \left(-\alpha \right)=\cos \alpha \,,}
t
g
(
− ‚ąí -->
α őĪ -->
)
=
− ‚ąí -->
t
g
α őĪ -->
,
{\displaystyle \mathop {\mathrm {tg} } \,\left(-\alpha \right)=-\mathop {\mathrm {tg} } \,\alpha \,,}
c
t
g
(
− ‚ąí -->
α őĪ -->
)
=
− ‚ąí -->
c
t
g
α őĪ -->
,
{\displaystyle \mathop {\mathrm {ctg} } \,\left(-\alpha \right)=-\mathop {\mathrm {ctg} } \,\alpha \,,}
sec
‚Ā° -->
(
− ‚ąí -->
α őĪ -->
)
=
sec
‚Ā° -->
α őĪ -->
,
{\displaystyle \sec \left(-\alpha \right)=\sec \alpha \,,}
c
o
s
e
c
(
− ‚ąí -->
α őĪ -->
)
=
− ‚ąí -->
c
o
s
e
c
α őĪ -->
.
{\displaystyle \mathop {\mathrm {cosec} } \,\left(-\alpha \right)=-\mathop {\mathrm {cosec} } \,\alpha \,.}
–§—É–Ĺ–ļ—Ü–ł–ł
sin
‚Ā° -->
x
,
cos
‚Ā° -->
x
,
sec
‚Ā° -->
x
,
c
o
s
e
c
x
{\displaystyle \sin x,\;\cos x,\;\sec x,\;\mathrm {cosec} \,x}
–Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā –Ņ–Ķ—Ä–ł–ĺ–ī–ĺ–ľ
2
π ŌÄ -->
{\displaystyle 2\pi }
t
g
x
{\displaystyle \mathrm {tg} \,x}
c
t
g
x
{\displaystyle \mathrm {ctg} \,x}
π ŌÄ -->
{\displaystyle \pi }
–§–ĺ—Ä–ľ—É–Ľ–į–ľ–ł –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ—č —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–≥–ĺ –≤–ł–ī–į:
f
(
n
π ŌÄ -->
+
α őĪ -->
)
=
± ¬Ī -->
f
(
α őĪ -->
)
,
{\displaystyle f(n\pi +\alpha )=\pm f(\alpha ),}
f
(
n
π ŌÄ -->
− ‚ąí -->
α őĪ -->
)
=
± ¬Ī -->
f
(
α őĪ -->
)
,
{\displaystyle f(n\pi -\alpha )=\pm f(\alpha ),}
f
(
(
2
n
+
1
)
π ŌÄ -->
2
+
α őĪ -->
)
=
± ¬Ī -->
g
(
α őĪ -->
)
,
{\displaystyle f\left({\frac {(2n+1)\pi }{2}}+\alpha \right)=\pm g(\alpha ),}
f
(
(
2
n
+
1
)
π ŌÄ -->
2
− ‚ąí -->
α őĪ -->
)
=
± ¬Ī -->
g
(
α őĪ -->
)
.
{\displaystyle f\left({\frac {(2n+1)\pi }{2}}-\alpha \right)=\pm g(\alpha ).}
–ó–ī–Ķ—Ā—Ć
f
{\displaystyle f}
g
{\displaystyle g}
n
{\displaystyle n}
—Ü–Ķ–Ľ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ . –ü–Ķ—Ä–Ķ–ī –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ —Ā—ā–į–≤–ł—ā—Ā—Ź —ā–ĺ—ā –∑–Ĺ–į–ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ł–ľ–Ķ–Ķ—ā –ł—Ā—Ö–ĺ–ī–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź –≤ –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ļ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–ĺ–Ļ —á–Ķ—ā–≤–Ķ—Ä—ā–ł –Ņ—Ä–ł —É—Ā–Ľ–ĺ–≤–ł–ł, —á—ā–ĺ —É–≥–ĺ–Ľ
α őĪ -->
{\displaystyle \alpha }
cos
‚Ā° -->
(
π ŌÄ -->
2
− ‚ąí -->
α őĪ -->
)
=
sin
‚Ā° -->
α őĪ -->
,
{\displaystyle \cos \left({\frac {\pi }{2}}-\alpha \right)=\sin \alpha \,,}
cos
‚Ā° -->
(
90
∘ ‚ąė -->
− ‚ąí -->
α őĪ -->
)
=
sin
‚Ā° -->
α őĪ -->
.
{\displaystyle \cos \left(90^{\circ }-\alpha \right)=\sin \alpha \,.}
–Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–ł—Ź:
α őĪ -->
{\displaystyle \alpha }
π ŌÄ -->
2
− ‚ąí -->
α őĪ -->
{\displaystyle {\frac {\pi }{2}}-\alpha }
π ŌÄ -->
2
+
α őĪ -->
{\displaystyle {\frac {\pi }{2}}+\alpha }
π ŌÄ -->
− ‚ąí -->
α őĪ -->
{\displaystyle \pi -\alpha }
π ŌÄ -->
+
α őĪ -->
{\displaystyle \pi +\alpha }
3
π ŌÄ -->
2
− ‚ąí -->
α őĪ -->
{\displaystyle {\frac {3\,\pi }{2}}-\alpha }
3
π ŌÄ -->
2
+
α őĪ -->
{\displaystyle {\frac {3\,\pi }{2}}+\alpha }
2
π ŌÄ -->
− ‚ąí -->
α őĪ -->
{\displaystyle 2\,\pi -\alpha }
sin
‚Ā° -->
α őĪ -->
{\displaystyle \sin \alpha }
cos
‚Ā° -->
α őĪ -->
{\displaystyle \cos \alpha }
cos
‚Ā° -->
α őĪ -->
{\displaystyle \cos \alpha }
sin
‚Ā° -->
α őĪ -->
{\displaystyle \sin \alpha }
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
{\displaystyle -\sin \alpha }
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
{\displaystyle -\cos \alpha }
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
{\displaystyle -\cos \alpha }
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
{\displaystyle -\sin \alpha }
cos
‚Ā° -->
α őĪ -->
{\displaystyle \cos \alpha }
sin
‚Ā° -->
α őĪ -->
{\displaystyle \sin \alpha }
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
{\displaystyle -\sin \alpha }
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
{\displaystyle -\cos \alpha }
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
{\displaystyle -\cos \alpha }
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
{\displaystyle -\sin \alpha }
sin
‚Ā° -->
α őĪ -->
{\displaystyle \sin \alpha }
cos
‚Ā° -->
α őĪ -->
{\displaystyle \cos \alpha }
tg
α őĪ -->
{\displaystyle \operatorname {tg} \,\alpha }
ctg
α őĪ -->
{\displaystyle \operatorname {ctg} \,\alpha }
− ‚ąí -->
ctg
α őĪ -->
{\displaystyle -\operatorname {ctg} \,\alpha }
− ‚ąí -->
tg
α őĪ -->
{\displaystyle -\operatorname {tg} \,\alpha }
tg
α őĪ -->
{\displaystyle \operatorname {tg} \,\alpha }
ctg
α őĪ -->
{\displaystyle \operatorname {ctg} \,\alpha }
− ‚ąí -->
ctg
α őĪ -->
{\displaystyle -\operatorname {ctg} \,\alpha }
− ‚ąí -->
tg
α őĪ -->
{\displaystyle -\operatorname {tg} \,\alpha }
ctg
α őĪ -->
{\displaystyle \operatorname {ctg} \,\alpha }
tg
α őĪ -->
{\displaystyle \operatorname {tg} \,\alpha }
− ‚ąí -->
tg
α őĪ -->
{\displaystyle -\operatorname {tg} \,\alpha }
− ‚ąí -->
ctg
α őĪ -->
{\displaystyle -\operatorname {ctg} \,\alpha }
ctg
α őĪ -->
{\displaystyle \operatorname {ctg} \,\alpha }
tg
α őĪ -->
{\displaystyle \operatorname {tg} \,\alpha }
− ‚ąí -->
tg
α őĪ -->
{\displaystyle -\operatorname {tg} \,\alpha }
− ‚ąí -->
ctg
α őĪ -->
{\displaystyle -\operatorname {ctg} \,\alpha }
–ė–Ĺ—ā–Ķ—Ä–Ķ—Ā—É—é—Č–ł–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–ł—Ź —ā–į–ļ –∂–Ķ –ľ–ĺ–≥—É—ā –Ľ–Ķ–≥–ļ–ĺ –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ—č —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł–Ķ–ľ —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ĺ–į –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–ó–Ĺ–į—á–Ķ–Ĺ–ł—Ź —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —Ā—É–ľ–ľ—č –ł —Ä–į–∑–Ĺ–ĺ—Ā—ā–ł –ī–≤—É—Ö —É–≥–Ľ–ĺ–≤:
sin
‚Ā° -->
(
α őĪ -->
± ¬Ī -->
β ő≤ -->
)
=
sin
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
± ¬Ī -->
cos
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
,
{\displaystyle \sin \left(\alpha \pm \beta \right)=\sin \alpha \,\cos \beta \pm \cos \alpha \,\sin \beta ,}
cos
‚Ā° -->
(
α őĪ -->
± ¬Ī -->
β ő≤ -->
)
=
cos
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
∓ ‚ąď -->
sin
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
,
{\displaystyle \cos \left(\alpha \pm \beta \right)=\cos \alpha \,\cos \beta \mp \sin \alpha \,\sin \beta ,}
tg
‚Ā° -->
(
α őĪ -->
± ¬Ī -->
β ő≤ -->
)
=
tg
α őĪ -->
± ¬Ī -->
tg
β ő≤ -->
1
∓ ‚ąď -->
tg
α őĪ -->
tg
β ő≤ -->
,
{\displaystyle \operatorname {tg} \left(\alpha \pm \beta \right)={\frac {\operatorname {tg} \,\alpha \pm \operatorname {tg} \,\beta }{1\mp \operatorname {tg} \,\alpha \,\operatorname {tg} \,\beta }},}
ctg
‚Ā° -->
(
α őĪ -->
± ¬Ī -->
β ő≤ -->
)
=
ctg
α őĪ -->
ctg
β ő≤ -->
∓ ‚ąď -->
1
ctg
β ő≤ -->
± ¬Ī -->
ctg
α őĪ -->
.
{\displaystyle \operatorname {ctg} \left(\alpha \pm \beta \right)={\frac {\operatorname {ctg} \,\alpha \,\operatorname {ctg} \,\beta \mp 1}{\operatorname {ctg} \,\beta \pm \operatorname {ctg} \,\alpha }}.}
–ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ—č–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ī–Ľ—Ź —Ā—É–ľ–ľ—č —ā—Ä—Ď—Ö —É–≥–Ľ–ĺ–≤:
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
+
γ ő≥ -->
)
=
sin
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
cos
‚Ā° -->
γ ő≥ -->
+
cos
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
cos
‚Ā° -->
γ ő≥ -->
+
cos
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
sin
‚Ā° -->
γ ő≥ -->
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
sin
‚Ā° -->
γ ő≥ -->
,
{\displaystyle \sin \left(\alpha +\beta +\gamma \right)=\sin \alpha \cos \beta \cos \gamma +\cos \alpha \sin \beta \cos \gamma +\cos \alpha \cos \beta \sin \gamma -\sin \alpha \sin \beta \sin \gamma ,}
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
+
γ ő≥ -->
)
=
cos
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
cos
‚Ā° -->
γ ő≥ -->
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
cos
‚Ā° -->
γ ő≥ -->
− ‚ąí -->
sin
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
sin
‚Ā° -->
γ ő≥ -->
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
sin
‚Ā° -->
γ ő≥ -->
.
{\displaystyle \cos \left(\alpha +\beta +\gamma \right)=\cos \alpha \cos \beta \cos \gamma -\sin \alpha \sin \beta \cos \gamma -\sin \alpha \cos \beta \sin \gamma -\cos \alpha \sin \beta \sin \gamma .}
–§–ĺ—Ä–ľ—É–Ľ—č –ī–≤–ĺ–Ļ–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į:
sin
‚Ā° -->
2
α őĪ -->
=
2
sin
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
α őĪ -->
=
2
tg
α őĪ -->
1
+
tg
2
‚Ā° -->
α őĪ -->
=
2
ctg
α őĪ -->
1
+
ctg
2
‚Ā° -->
α őĪ -->
=
2
tg
α őĪ -->
+
ctg
α őĪ -->
,
{\displaystyle \sin 2\alpha =2\sin \alpha \cos \alpha ={\frac {2\,\operatorname {tg} \,\alpha }{1+\operatorname {tg} ^{2}\alpha }}={\frac {2\,\operatorname {ctg} \,\alpha }{1+\operatorname {ctg} ^{2}\alpha }}={\frac {2}{\operatorname {tg} \,\alpha +\operatorname {ctg} \,\alpha }},}
cos
‚Ā° -->
2
α őĪ -->
=
cos
2
‚Ā° -->
α őĪ -->
− ‚ąí -->
sin
2
‚Ā° -->
α őĪ -->
=
2
cos
2
‚Ā° -->
α őĪ -->
− ‚ąí -->
1
=
1
− ‚ąí -->
2
sin
2
‚Ā° -->
α őĪ -->
=
1
− ‚ąí -->
tg
2
‚Ā° -->
α őĪ -->
1
+
tg
2
‚Ā° -->
α őĪ -->
=
ctg
2
‚Ā° -->
α őĪ -->
− ‚ąí -->
1
ctg
2
‚Ā° -->
α őĪ -->
+
1
=
ctg
α őĪ -->
− ‚ąí -->
tg
α őĪ -->
ctg
α őĪ -->
+
tg
α őĪ -->
,
{\displaystyle \cos 2\alpha =\cos ^{2}\alpha \,-\,\sin ^{2}\alpha =2\cos ^{2}\alpha \,-\,1=1\,-\,2\sin ^{2}\alpha ={\frac {1-\operatorname {tg} ^{2}\alpha }{1+\operatorname {tg} ^{2}\alpha }}={\frac {\operatorname {ctg} ^{2}\alpha -1}{\operatorname {ctg} ^{2}\alpha +1}}={\frac {\operatorname {ctg} \,\alpha -\operatorname {tg} \,\alpha }{\operatorname {ctg} \,\alpha +\operatorname {tg} \,\alpha }},}
tg
2
α őĪ -->
=
2
tg
α őĪ -->
1
− ‚ąí -->
tg
2
‚Ā° -->
α őĪ -->
=
2
ctg
α őĪ -->
ctg
2
‚Ā° -->
α őĪ -->
− ‚ąí -->
1
=
2
ctg
α őĪ -->
− ‚ąí -->
tg
α őĪ -->
,
{\displaystyle \operatorname {tg} \,2\alpha ={\frac {2\,\operatorname {tg} \,\alpha }{1-\operatorname {tg} ^{2}\alpha }}={\frac {2\,\operatorname {ctg} \,\alpha }{\operatorname {ctg} ^{2}\alpha -1}}={\frac {2}{\operatorname {ctg} \,\alpha -\operatorname {tg} \,\alpha }},}
ctg
2
α őĪ -->
=
ctg
2
‚Ā° -->
α őĪ -->
− ‚ąí -->
1
2
ctg
α őĪ -->
=
ctg
α őĪ -->
− ‚ąí -->
tg
α őĪ -->
2
.
{\displaystyle \operatorname {ctg} \,2\alpha ={\frac {\operatorname {ctg} ^{2}\alpha -1}{2\,\operatorname {ctg} \,\alpha }}={\frac {\operatorname {ctg} \,\alpha -\operatorname {tg} \,\alpha }{2}}.}
–§–ĺ—Ä–ľ—É–Ľ—č —ā—Ä–ĺ–Ļ–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į:
sin
3
α őĪ -->
=
3
sin
‚Ā° -->
α őĪ -->
− ‚ąí -->
4
sin
3
‚Ā° -->
α őĪ -->
,
{\displaystyle \sin \,3\alpha =3\sin \alpha -4\sin ^{3}\alpha ,}
cos
3
α őĪ -->
=
4
cos
3
‚Ā° -->
α őĪ -->
− ‚ąí -->
3
cos
‚Ā° -->
α őĪ -->
,
{\displaystyle \cos \,3\alpha =4\cos ^{3}\alpha -3\cos \alpha ,}
tg
3
α őĪ -->
=
3
tg
α őĪ -->
− ‚ąí -->
tg
3
α őĪ -->
1
− ‚ąí -->
3
tg
2
α őĪ -->
,
{\displaystyle \operatorname {tg} \,3\alpha ={\frac {3\,\operatorname {tg} \,\alpha -\operatorname {tg} ^{3}\,\alpha }{1-3\,\operatorname {tg} ^{2}\,\alpha }},}
ctg
3
α őĪ -->
=
ctg
3
α őĪ -->
− ‚ąí -->
3
ctg
α őĪ -->
3
ctg
2
α őĪ -->
− ‚ąí -->
1
.
{\displaystyle \operatorname {ctg} \,3\alpha ={\frac {\operatorname {ctg} ^{3}\,\alpha -3\,\operatorname {ctg} \,\alpha }{3\,\operatorname {ctg} ^{2}\,\alpha -1}}.}
–ü—Ä–ĺ—á–ł–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ī–Ľ—Ź –ļ—Ä–į—ā–Ĺ—č—Ö —É–≥–Ľ–ĺ–≤:
sin
4
α őĪ -->
=
cos
‚Ā° -->
α őĪ -->
(
4
sin
‚Ā° -->
α őĪ -->
− ‚ąí -->
8
sin
3
‚Ā° -->
α őĪ -->
)
,
{\displaystyle \sin \,4\alpha =\cos \alpha \left(4\sin \alpha -8\sin ^{3}\alpha \right),}
cos
4
α őĪ -->
=
8
cos
4
‚Ā° -->
α őĪ -->
− ‚ąí -->
8
cos
2
‚Ā° -->
α őĪ -->
+
1
=
8
sin
4
‚Ā° -->
α őĪ -->
− ‚ąí -->
8
sin
2
‚Ā° -->
α őĪ -->
+
1
,
{\displaystyle \cos \,4\alpha =8\cos ^{4}\alpha -8\cos ^{2}\alpha +1=8\sin ^{4}\alpha -8\sin ^{2}\alpha +1,}
tg
4
α őĪ -->
=
4
tg
α őĪ -->
− ‚ąí -->
4
tg
3
α őĪ -->
1
− ‚ąí -->
6
tg
2
α őĪ -->
+
tg
4
α őĪ -->
,
{\displaystyle \operatorname {tg} \,4\alpha ={\frac {4\,\operatorname {tg} \,\alpha -4\,\operatorname {tg} ^{3}\,\alpha }{1-6\,\operatorname {tg} ^{2}\,\alpha +\operatorname {tg} ^{4}\,\alpha }},}
ctg
4
α őĪ -->
=
ctg
4
α őĪ -->
− ‚ąí -->
6
ctg
2
α őĪ -->
+
1
4
ctg
3
α őĪ -->
− ‚ąí -->
4
ctg
α őĪ -->
,
{\displaystyle \operatorname {ctg} \,4\alpha ={\frac {\operatorname {ctg} ^{4}\,\alpha -6\,\operatorname {ctg} ^{2}\,\alpha +1}{4\,\operatorname {ctg} ^{3}\,\alpha -4\,\operatorname {ctg} \,\alpha }},}
sin
5
α őĪ -->
=
16
sin
5
‚Ā° -->
α őĪ -->
− ‚ąí -->
20
sin
3
‚Ā° -->
α őĪ -->
+
5
sin
‚Ā° -->
α őĪ -->
,
{\displaystyle \sin \,5\alpha =16\sin ^{5}\alpha -20\sin ^{3}\alpha +5\sin \alpha ,}
cos
5
α őĪ -->
=
16
cos
5
‚Ā° -->
α őĪ -->
− ‚ąí -->
20
cos
3
‚Ā° -->
α őĪ -->
+
5
cos
‚Ā° -->
α őĪ -->
,
{\displaystyle \cos \,5\alpha =16\cos ^{5}\alpha -20\cos ^{3}\alpha +5\cos \alpha ,}
tg
5
α őĪ -->
=
tg
‚Ā° -->
α őĪ -->
tg
4
‚Ā° -->
α őĪ -->
− ‚ąí -->
10
tg
2
‚Ā° -->
α őĪ -->
+
5
5
tg
4
‚Ā° -->
α őĪ -->
− ‚ąí -->
10
tg
2
‚Ā° -->
α őĪ -->
+
1
,
{\displaystyle \operatorname {tg} \,5\alpha =\operatorname {tg} \alpha {\frac {\operatorname {tg} ^{4}\alpha -10\operatorname {tg} ^{2}\alpha +5}{5\operatorname {tg} ^{4}\alpha -10\operatorname {tg} ^{2}\alpha +1}},}
ctg
5
α őĪ -->
=
ctg
‚Ā° -->
α őĪ -->
ctg
4
‚Ā° -->
α őĪ -->
− ‚ąí -->
10
ctg
2
‚Ā° -->
α őĪ -->
+
5
5
ctg
4
‚Ā° -->
α őĪ -->
− ‚ąí -->
10
ctg
2
‚Ā° -->
α őĪ -->
+
1
,
{\displaystyle \operatorname {ctg} \,5\alpha =\operatorname {ctg} \alpha {\frac {\operatorname {ctg} ^{4}\alpha -10\operatorname {ctg} ^{2}\alpha +5}{5\operatorname {ctg} ^{4}\alpha -10\operatorname {ctg} ^{2}\alpha +1}},}
sin
‚Ā° -->
(
n
α őĪ -->
)
=
2
n
− ‚ąí -->
1
∏ ‚ąŹ -->
k
=
0
n
− ‚ąí -->
1
sin
‚Ā° -->
(
α őĪ -->
+
π ŌÄ -->
k
n
)
{\displaystyle \sin(n\alpha )=2^{n-1}\prod _{k=0}^{n-1}\sin \left(\alpha +{\frac {\pi k}{n}}\right)}
–≥–į–ľ–ľ–į-—Ą—É–Ĺ–ļ—Ü–ł–ł .–ė–∑ —Ą–ĺ—Ä–ľ—É–Ľ—č –ú—É–į–≤—Ä–į –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–ł—ā—Ć —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ĺ–Ī—Č–ł–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –ī–Ľ—Ź –ļ—Ä–į—ā–Ĺ—č—Ö —É–≥–Ľ–ĺ–≤:
sin
‚Ā° -->
(
n
α őĪ -->
)
=
∑ ‚ąĎ -->
k
=
0
[
(
n
− ‚ąí -->
1
)
/
2
]
(
− ‚ąí -->
1
)
k
(
n
2
k
+
1
)
cos
n
− ‚ąí -->
2
k
− ‚ąí -->
1
‚Ā° -->
α őĪ -->
sin
2
k
+
1
‚Ā° -->
α őĪ -->
,
{\displaystyle \sin(n\alpha )=\sum _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\cos ^{n-2k-1}\alpha \,\sin ^{2k+1}\alpha ,}
cos
‚Ā° -->
(
n
α őĪ -->
)
=
∑ ‚ąĎ -->
k
=
0
[
n
/
2
]
(
− ‚ąí -->
1
)
k
(
n
2
k
)
cos
n
− ‚ąí -->
2
k
‚Ā° -->
α őĪ -->
sin
2
k
‚Ā° -->
α őĪ -->
,
{\displaystyle \cos(n\alpha )=\sum _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\cos ^{n-2k}\alpha \,\sin ^{2k}\alpha ,}
t
g
(
n
α őĪ -->
)
=
sin
‚Ā° -->
(
n
α őĪ -->
)
cos
‚Ā° -->
(
n
α őĪ -->
)
=
∑ ‚ąĎ -->
k
=
0
[
(
n
− ‚ąí -->
1
)
/
2
]
(
− ‚ąí -->
1
)
k
(
n
2
k
+
1
)
t
g
2
k
+
1
α őĪ -->
∑ ‚ąĎ -->
k
=
0
[
n
/
2
]
(
− ‚ąí -->
1
)
k
(
n
2
k
)
t
g
2
k
α őĪ -->
,
{\displaystyle \mathrm {tg} (n\alpha )={\frac {\sin(n\alpha )}{\cos(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {tg} ^{2k+1}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {tg} ^{2k}\alpha }}},}
c
t
g
(
n
α őĪ -->
)
=
cos
‚Ā° -->
(
n
α őĪ -->
)
sin
‚Ā° -->
(
n
α őĪ -->
)
=
∑ ‚ąĎ -->
k
=
0
[
n
/
2
]
(
− ‚ąí -->
1
)
k
(
n
2
k
)
c
t
g
n
− ‚ąí -->
2
k
α őĪ -->
∑ ‚ąĎ -->
k
=
0
[
(
n
− ‚ąí -->
1
)
/
2
]
(
− ‚ąí -->
1
)
k
(
n
2
k
+
1
)
c
t
g
n
− ‚ąí -->
2
k
− ‚ąí -->
1
α őĪ -->
,
{\displaystyle \mathrm {ctg} (n\alpha )={\frac {\cos(n\alpha )}{\sin(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {ctg} ^{n-2k}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {ctg} ^{n-2k-1}\alpha }}},}
–≥–ī–Ķ
[
n
]
{\displaystyle [n]}
—Ü–Ķ–Ľ–į—Ź —á–į—Ā—ā—Ć —á–ł—Ā–Ľ–į
n
{\displaystyle n}
(
n
k
)
{\displaystyle {\binom {n}{k}}}
–Ī–ł–Ĺ–ĺ–ľ–ł–į–Ľ—Ć–Ĺ—č–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā .
–§–ĺ—Ä–ľ—É–Ľ—č –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į:
sin
‚Ā° -->
α őĪ -->
2
=
1
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
2
,
0
⩽ ‚©Ĺ -->
α őĪ -->
⩽ ‚©Ĺ -->
2
π ŌÄ -->
,
{\displaystyle \sin {\frac {\alpha }{2}}={\sqrt {\frac {1-\cos \alpha }{2}}},\quad 0\leqslant \alpha \leqslant 2\pi ,}
cos
‚Ā° -->
α őĪ -->
2
=
1
+
cos
‚Ā° -->
α őĪ -->
2
,
− ‚ąí -->
π ŌÄ -->
⩽ ‚©Ĺ -->
α őĪ -->
⩽ ‚©Ĺ -->
π ŌÄ -->
,
{\displaystyle \cos {\frac {\alpha }{2}}={\sqrt {\frac {1+\cos \alpha }{2}}},\quad -\pi \leqslant \alpha \leqslant \pi ,}
tg
α őĪ -->
2
=
1
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
α őĪ -->
=
sin
‚Ā° -->
α őĪ -->
1
+
cos
‚Ā° -->
α őĪ -->
,
{\displaystyle \operatorname {tg} \,{\frac {\alpha }{2}}={\frac {1-\cos \alpha }{\sin \alpha }}={\frac {\sin \alpha }{1+\cos \alpha }},}
ctg
α őĪ -->
2
=
sin
‚Ā° -->
α őĪ -->
1
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
=
1
+
cos
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
α őĪ -->
,
{\displaystyle \operatorname {ctg} \,{\frac {\alpha }{2}}={\frac {\sin \alpha }{1-\cos \alpha }}={\frac {1+\cos \alpha }{\sin \alpha }},}
tg
α őĪ -->
2
=
1
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
1
+
cos
‚Ā° -->
α őĪ -->
,
0
⩽ ‚©Ĺ -->
α őĪ -->
<
π ŌÄ -->
,
{\displaystyle \operatorname {tg} \,{\frac {\alpha }{2}}={\sqrt {\frac {1-\cos \alpha }{1+\cos \alpha }}},\quad 0\leqslant \alpha <\pi ,}
ctg
α őĪ -->
2
=
1
+
cos
‚Ā° -->
α őĪ -->
1
− ‚ąí -->
cos
‚Ā° -->
α őĪ -->
,
0
<
α őĪ -->
⩽ ‚©Ĺ -->
π ŌÄ -->
.
{\displaystyle \operatorname {ctg} \,{\frac {\alpha }{2}}={\sqrt {\frac {1+\cos \alpha }{1-\cos \alpha }}},\quad 0<\alpha \leqslant \pi .}
–§–ĺ—Ä–ľ—É–Ľ—č –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ī–≤—É—Ö —É–≥–Ľ–ĺ–≤:
sin
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
=
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
− ‚ąí -->
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
2
,
{\displaystyle \sin \alpha \sin \beta ={\frac {\cos(\alpha -\beta )-\cos(\alpha +\beta )}{2}},}
sin
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
=
sin
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
+
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
2
,
{\displaystyle \sin \alpha \cos \beta ={\frac {\sin(\alpha -\beta )+\sin(\alpha +\beta )}{2}},}
cos
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
=
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
+
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
2
,
{\displaystyle \cos \alpha \cos \beta ={\frac {\cos(\alpha -\beta )+\cos(\alpha +\beta )}{2}},}
tg
α őĪ -->
tg
β ő≤ -->
=
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
− ‚ąí -->
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
+
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
,
{\displaystyle \operatorname {tg} \,\alpha \,\operatorname {tg} \,\beta ={\frac {\cos(\alpha -\beta )-\cos(\alpha +\beta )}{\cos(\alpha -\beta )+\cos(\alpha +\beta )}},}
tg
α őĪ -->
ctg
β ő≤ -->
=
sin
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
+
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
− ‚ąí -->
sin
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
,
{\displaystyle \operatorname {tg} \,\alpha \,\operatorname {ctg} \,\beta ={\frac {\sin(\alpha -\beta )+\sin(\alpha +\beta )}{\sin(\alpha +\beta )-\sin(\alpha -\beta )}},}
ctg
α őĪ -->
ctg
β ő≤ -->
=
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
+
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
)
− ‚ąí -->
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
)
.
{\displaystyle \operatorname {ctg} \,\alpha \,\operatorname {ctg} \,\beta ={\frac {\cos(\alpha -\beta )+\cos(\alpha +\beta )}{\cos(\alpha -\beta )-\cos(\alpha +\beta )}}.}
–ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ—č–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ —Ā–ł–Ĺ—É—Ā–ĺ–≤ –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā–ĺ–≤ —ā—Ä—Ď—Ö —É–≥–Ľ–ĺ–≤:
sin
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
sin
‚Ā° -->
γ ő≥ -->
=
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
− ‚ąí -->
γ ő≥ -->
)
+
sin
‚Ā° -->
(
β ő≤ -->
+
γ ő≥ -->
− ‚ąí -->
α őĪ -->
)
+
sin
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
+
γ ő≥ -->
)
− ‚ąí -->
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
+
γ ő≥ -->
)
4
,
{\displaystyle \sin \alpha \sin \beta \sin \gamma ={\frac {\sin(\alpha +\beta -\gamma )+\sin(\beta +\gamma -\alpha )+\sin(\alpha -\beta +\gamma )-\sin(\alpha +\beta +\gamma )}{4}},}
sin
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
cos
‚Ā° -->
γ ő≥ -->
=
− ‚ąí -->
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
− ‚ąí -->
γ ő≥ -->
)
+
cos
‚Ā° -->
(
β ő≤ -->
+
γ ő≥ -->
− ‚ąí -->
α őĪ -->
)
+
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
+
γ ő≥ -->
)
− ‚ąí -->
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
+
γ ő≥ -->
)
4
,
{\displaystyle \sin \alpha \sin \beta \cos \gamma ={\frac {-\cos(\alpha +\beta -\gamma )+\cos(\beta +\gamma -\alpha )+\cos(\alpha -\beta +\gamma )-\cos(\alpha +\beta +\gamma )}{4}},}
sin
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
cos
‚Ā° -->
γ ő≥ -->
=
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
− ‚ąí -->
γ ő≥ -->
)
− ‚ąí -->
sin
‚Ā° -->
(
β ő≤ -->
+
γ ő≥ -->
− ‚ąí -->
α őĪ -->
)
+
sin
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
+
γ ő≥ -->
)
− ‚ąí -->
sin
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
+
γ ő≥ -->
)
4
,
{\displaystyle \sin \alpha \cos \beta \cos \gamma ={\frac {\sin(\alpha +\beta -\gamma )-\sin(\beta +\gamma -\alpha )+\sin(\alpha -\beta +\gamma )-\sin(\alpha +\beta +\gamma )}{4}},}
cos
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
cos
‚Ā° -->
γ ő≥ -->
=
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
− ‚ąí -->
γ ő≥ -->
)
+
cos
‚Ā° -->
(
β ő≤ -->
+
γ ő≥ -->
− ‚ąí -->
α őĪ -->
)
+
cos
‚Ā° -->
(
α őĪ -->
− ‚ąí -->
β ő≤ -->
+
γ ő≥ -->
)
+
cos
‚Ā° -->
(
α őĪ -->
+
β ő≤ -->
+
γ ő≥ -->
)
4
.
{\displaystyle \cos \alpha \cos \beta \cos \gamma ={\frac {\cos(\alpha +\beta -\gamma )+\cos(\beta +\gamma -\alpha )+\cos(\alpha -\beta +\gamma )+\cos(\alpha +\beta +\gamma )}{4}}.}
–§–ĺ—Ä–ľ—É–Ľ—č –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–ĺ–≤ –ł –ļ–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā–ĺ–≤ —ā—Ä—Ď—Ö —É–≥–Ľ–ĺ–≤ –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ–Ľ—É—á–ł—ā—Ć, –Ņ–ĺ–ī–Ķ–Ľ–ł–≤ –Ņ—Ä–į–≤—č–Ķ –ł –Ľ–Ķ–≤—č–Ķ —á–į—Ā—ā–ł —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł—Ö —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–Ĺ—č—Ö –≤—č—ą–Ķ.
sin
2
‚Ā° -->
α őĪ -->
=
1
− ‚ąí -->
cos
‚Ā° -->
2
α őĪ -->
2
=
tg
2
α őĪ -->
1
+
tg
2
α őĪ -->
,
{\displaystyle \sin ^{2}\alpha ={\frac {1-\cos 2\,\alpha }{2}}={\frac {\operatorname {tg} ^{2}\,\alpha }{1+\operatorname {tg} ^{2}\,\alpha }},}
cos
2
‚Ā° -->
α őĪ -->
=
1
+
cos
‚Ā° -->
2
α őĪ -->
2
=
ctg
2
α őĪ -->
1
+
ctg
2
α őĪ -->
,
{\displaystyle \cos ^{2}\alpha ={\frac {1+\cos 2\,\alpha }{2}}={\frac {\operatorname {ctg} ^{2}\,\alpha }{1+\operatorname {ctg} ^{2}\,\alpha }},}
tg
2
α őĪ -->
=
1
− ‚ąí -->
cos
‚Ā° -->
2
α őĪ -->
1
+
cos
‚Ā° -->
2
α őĪ -->
=
sin
2
α őĪ -->
1
− ‚ąí -->
sin
2
α őĪ -->
,
{\displaystyle \operatorname {tg} ^{2}\,\alpha ={\frac {1-\cos 2\,\alpha }{1+\cos 2\,\alpha }}={\frac {\operatorname {sin} ^{2}\,\alpha }{1-\operatorname {sin} ^{2}\,\alpha }},}
ctg
2
α őĪ -->
=
1
+
cos
‚Ā° -->
2
α őĪ -->
1
− ‚ąí -->
cos
‚Ā° -->
2
α őĪ -->
=
cos
2
α őĪ -->
1
− ‚ąí -->
cos
2
α őĪ -->
,
{\displaystyle \operatorname {ctg} ^{2}\,\alpha ={\frac {1+\cos 2\,\alpha }{1-\cos 2\,\alpha }}={\frac {\operatorname {cos} ^{2}\,\alpha }{1-\operatorname {cos} ^{2}\,\alpha }},}
sin
3
‚Ā° -->
α őĪ -->
=
3
sin
‚Ā° -->
α őĪ -->
− ‚ąí -->
sin
‚Ā° -->
3
α őĪ -->
4
,
{\displaystyle \sin ^{3}\alpha ={\frac {3\sin \alpha -\sin 3\,\alpha }{4}},}
cos
3
‚Ā° -->
α őĪ -->
=
3
cos
‚Ā° -->
α őĪ -->
+
cos
‚Ā° -->
3
α őĪ -->
4
,
{\displaystyle \cos ^{3}\alpha ={\frac {3\cos \alpha +\cos 3\,\alpha }{4}},}
tg
3
α őĪ -->
=
3
sin
‚Ā° -->
α őĪ -->
− ‚ąí -->
sin
‚Ā° -->
3
α őĪ -->
3
cos
‚Ā° -->
α őĪ -->
+
cos
‚Ā° -->
3
α őĪ -->
,
{\displaystyle \operatorname {tg} ^{3}\,\alpha ={\frac {3\sin \alpha -\sin 3\,\alpha }{3\cos \alpha +\cos 3\,\alpha }},}
ctg
3
α őĪ -->
=
3
cos
‚Ā° -->
α őĪ -->
+
cos
‚Ā° -->
3
α őĪ -->
3
sin
‚Ā° -->
α őĪ -->
− ‚ąí -->
sin
‚Ā° -->
3
α őĪ -->
,
{\displaystyle \operatorname {ctg} ^{3}\,\alpha ={\frac {3\cos \alpha +\cos 3\,\alpha }{3\sin \alpha -\sin 3\,\alpha }},}
sin
4
‚Ā° -->
α őĪ -->
=
cos
‚Ā° -->
4
α őĪ -->
− ‚ąí -->
4
cos
‚Ā° -->
2
α őĪ -->
+
3
8
,
{\displaystyle \sin ^{4}\alpha ={\frac {\cos 4\alpha -4\cos 2\,\alpha +3}{8}},}
cos
4
‚Ā° -->
α őĪ -->
=
cos
‚Ā° -->
4
α őĪ -->
+
4
cos
‚Ā° -->
2
α őĪ -->
+
3
8
,
{\displaystyle \cos ^{4}\alpha ={\frac {\cos 4\alpha +4\cos 2\,\alpha +3}{8}},}
tg
4
α őĪ -->
=
cos
‚Ā° -->
4
α őĪ -->
− ‚ąí -->
4
cos
‚Ā° -->
2
α őĪ -->
+
3
cos
‚Ā° -->
4
α őĪ -->
+
4
cos
‚Ā° -->
2
α őĪ -->
+
3
,
{\displaystyle \operatorname {tg} ^{4}\,\alpha ={\frac {\cos 4\alpha -4\cos 2\,\alpha +3}{\cos 4\alpha +4\cos 2\,\alpha +3}},}
ctg
4
α őĪ -->
=
cos
‚Ā° -->
4
α őĪ -->
+
4
cos
‚Ā° -->
2
α őĪ -->
+
3
cos
‚Ā° -->
4
α őĪ -->
− ‚ąí -->
4
cos
‚Ā° -->
2
α őĪ -->
+
3
.
{\displaystyle \operatorname {ctg} ^{4}\,\alpha ={\frac {\cos 4\alpha +4\cos 2\,\alpha +3}{\cos 4\alpha -4\cos 2\,\alpha +3}}.}
–ė–Ľ–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į
sin
‚Ā° -->
x
− ‚ąí -->
cos
‚Ā° -->
x
=
2
⋅ ‚čÖ -->
sin
‚Ā° -->
(
x
− ‚ąí -->
π ŌÄ -->
4
)
{\displaystyle \sin x-\cos x={\sqrt {2}}\cdot \sin \left(x-{\pi \over 4}\right)}
sin
‚Ā° -->
α őĪ -->
± ¬Ī -->
sin
‚Ā° -->
β ő≤ -->
=
2
sin
‚Ā° -->
α őĪ -->
± ¬Ī -->
β ő≤ -->
2
cos
‚Ā° -->
α őĪ -->
∓ ‚ąď -->
β ő≤ -->
2
,
{\displaystyle \sin \alpha \pm \sin \beta =2\sin {\frac {\alpha \pm \beta }{2}}\cos {\frac {\alpha \mp \beta }{2}},}
cos
‚Ā° -->
α őĪ -->
+
cos
‚Ā° -->
β ő≤ -->
=
2
cos
‚Ā° -->
α őĪ -->
+
β ő≤ -->
2
cos
‚Ā° -->
α őĪ -->
− ‚ąí -->
β ő≤ -->
2
,
{\displaystyle \cos \alpha +\cos \beta =2\cos {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}},}
cos
‚Ā° -->
α őĪ -->
− ‚ąí -->
cos
‚Ā° -->
β ő≤ -->
=
− ‚ąí -->
2
sin
‚Ā° -->
α őĪ -->
+
β ő≤ -->
2
sin
‚Ā° -->
α őĪ -->
− ‚ąí -->
β ő≤ -->
2
,
{\displaystyle \cos \alpha -\cos \beta =-2\sin {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}},}
tg
‚Ā° -->
α őĪ -->
± ¬Ī -->
tg
‚Ā° -->
β ő≤ -->
=
sin
‚Ā° -->
(
α őĪ -->
± ¬Ī -->
β ő≤ -->
)
cos
‚Ā° -->
α őĪ -->
cos
‚Ā° -->
β ő≤ -->
,
{\displaystyle \operatorname {tg} \alpha \pm \operatorname {tg} \beta ={\frac {\sin(\alpha \pm \beta )}{\cos \alpha \cos \beta }},}
ctg
‚Ā° -->
α őĪ -->
± ¬Ī -->
ctg
‚Ā° -->
β ő≤ -->
=
sin
‚Ā° -->
(
β ő≤ -->
± ¬Ī -->
α őĪ -->
)
sin
‚Ā° -->
α őĪ -->
sin
‚Ā° -->
β ő≤ -->
,
{\displaystyle \operatorname {ctg} \alpha \pm \operatorname {ctg} \beta ={\frac {\sin(\beta \pm \alpha )}{\sin \alpha \sin \beta }},}
1
± ¬Ī -->
sin
‚Ā° -->
2
α őĪ -->
=
(
sin
‚Ā° -->
α őĪ -->
± ¬Ī -->
cos
‚Ā° -->
α őĪ -->
)
2
,
{\displaystyle 1\pm \sin {2\alpha }=(\sin \alpha \pm \cos \alpha )^{2},}
sin
‚Ā° -->
α őĪ -->
± ¬Ī -->
cos
‚Ā° -->
α őĪ -->
=
2
⋅ ‚čÖ -->
sin
‚Ā° -->
(
α őĪ -->
± ¬Ī -->
π ŌÄ -->
4
)
.
{\displaystyle \sin \alpha \pm \cos \alpha ={\sqrt {2}}\cdot \sin \left(\alpha \pm {\pi \over 4}\right).}
–°—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ:
A
sin
‚Ā° -->
α őĪ -->
+
B
cos
‚Ā° -->
α őĪ -->
=
A
2
+
B
2
sin
‚Ā° -->
(
α őĪ -->
+
ϕ Ōē -->
)
,
{\displaystyle A\sin \alpha +B\cos \alpha ={\sqrt {A^{2}+B^{2}}}\;\sin(\alpha +\phi ),}
–≥–ī–Ķ —É–≥–ĺ–Ľ
ϕ Ōē -->
{\displaystyle \phi }
sin
‚Ā° -->
ϕ Ōē -->
=
B
A
2
+
B
2
,
{\displaystyle \sin \phi ={\frac {B}{\sqrt {A^{2}+B^{2}}}},}
cos
‚Ā° -->
ϕ Ōē -->
=
A
A
2
+
B
2
.
{\displaystyle \cos \phi ={\frac {A}{\sqrt {A^{2}+B^{2}}}}.}
–í—Ā–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ľ–ĺ–∂–Ĺ–ĺ –≤—č—Ä–į–∑–ł—ā—Ć —á–Ķ—Ä–Ķ–∑ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į:
sin
‚Ā° -->
x
=
sin
‚Ā° -->
x
1
=
2
sin
‚Ā° -->
x
2
cos
‚Ā° -->
x
2
sin
2
‚Ā° -->
x
2
+
cos
2
‚Ā° -->
x
2
=
2
tg
‚Ā° -->
x
2
1
+
tg
2
‚Ā° -->
x
2
,
{\displaystyle \sin x={\frac {\sin x}{1}}={\frac {2\sin {\frac {x}{2}}\cos {\frac {x}{2}}}{\sin ^{2}{\frac {x}{2}}+\cos ^{2}{\frac {x}{2}}}}={\frac {2\operatorname {tg} {\frac {x}{2}}}{1+\operatorname {tg} ^{2}{\frac {x}{2}}}},}
cos
‚Ā° -->
x
=
cos
‚Ā° -->
x
1
=
cos
2
‚Ā° -->
x
2
− ‚ąí -->
sin
2
‚Ā° -->
x
2
cos
2
‚Ā° -->
x
2
+
sin
2
‚Ā° -->
x
2
=
1
− ‚ąí -->
tg
2
‚Ā° -->
x
2
1
+
tg
2
‚Ā° -->
x
2
,
{\displaystyle \cos x={\frac {\cos x}{1}}={\frac {\cos ^{2}{\frac {x}{2}}-\sin ^{2}{\frac {x}{2}}}{\cos ^{2}{\frac {x}{2}}+\sin ^{2}{\frac {x}{2}}}}={\frac {1-\operatorname {tg} ^{2}{\frac {x}{2}}}{1+\operatorname {tg} ^{2}{\frac {x}{2}}}},}
tg
‚Ā° -->
x
=
sin
‚Ā° -->
x
cos
‚Ā° -->
x
=
2
tg
‚Ā° -->
x
2
1
− ‚ąí -->
tg
2
‚Ā° -->
x
2
,
{\displaystyle \operatorname {tg} ~x={\frac {\sin x}{\cos x}}={\frac {2\operatorname {tg} {\frac {x}{2}}}{1-\operatorname {tg} ^{2}{\frac {x}{2}}}},}
ctg
‚Ā° -->
x
=
cos
‚Ā° -->
x
sin
‚Ā° -->
x
=
1
− ‚ąí -->
tg
2
‚Ā° -->
x
2
2
tg
‚Ā° -->
x
2
,
{\displaystyle \operatorname {ctg} ~x={\frac {\cos x}{\sin x}}={\frac {1-\operatorname {tg} ^{2}{\frac {x}{2}}}{2\operatorname {tg} {\frac {x}{2}}}},}
sec
‚Ā° -->
x
=
1
cos
‚Ā° -->
x
=
1
+
tg
2
‚Ā° -->
x
2
1
− ‚ąí -->
tg
2
‚Ā° -->
x
2
,
{\displaystyle \sec x={\frac {1}{\cos x}}={\frac {1+\operatorname {tg} ^{2}{\frac {x}{2}}}{1-\operatorname {tg} ^{2}{\frac {x}{2}}}},}
cosec
‚Ā° -->
x
=
1
sin
‚Ā° -->
x
=
1
+
tg
2
‚Ā° -->
x
2
2
tg
‚Ā° -->
x
2
.
{\displaystyle \operatorname {cosec} ~x={\frac {1}{\sin x}}={\frac {1+\operatorname {tg} ^{2}{\frac {x}{2}}}{2\operatorname {tg} {\frac {x}{2}}}}.}
–Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ—č –≤ –≤–ł–ī–Ķ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤:
sin
‚Ā° -->
x
=
x
∏ ‚ąŹ -->
n
=
1
∞ ‚ąě -->
(
1
− ‚ąí -->
x
2
π ŌÄ -->
2
n
2
)
,
{\displaystyle \sin x=x\,\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),}
cos
‚Ā° -->
x
=
∏ ‚ąŹ -->
n
=
0
∞ ‚ąě -->
(
1
− ‚ąí -->
4
x
2
π ŌÄ -->
2
(
2
n
+
1
)
2
)
.
{\displaystyle \cos x=\prod _{n=0}^{\infty }\left(1-{\frac {4x^{2}}{\pi ^{2}(2n+1)^{2}}}\right).}
–≠—ā–ł —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź –Ņ—Ä–ł –Ľ—é–Ī–ĺ–ľ –∑–Ĺ–į—á–Ķ–Ĺ–ł–ł
x
{\displaystyle x}
–†–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į –≤ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—É—é –ī—Ä–ĺ–Ī—Ć :
t
g
‚Ā° -->
x
=
x
1
− ‚ąí -->
x
2
3
− ‚ąí -->
x
2
5
− ‚ąí -->
x
2
7
− ‚ąí -->
x
2
⋱ ‚čĪ -->
{\displaystyle \mathop {\rm {tg}} x={\frac {x}{1-{\frac {x^{2}}{3-{\frac {x^{2}}{5-{\frac {x^{2}}{7-{\frac {x^{2}}{\ddots }}}}}}}}}}}
–í—Ā–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ –ł –Ĺ–Ķ–ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ–ĺ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä—É–Ķ–ľ—č –Ĺ–į –≤—Ā–Ķ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź:
(
sin
‚Ā° -->
x
)
′
=
cos
‚Ā° -->
x
,
{\displaystyle (\sin x)'=\cos x\,,}
(
cos
‚Ā° -->
x
)
′
=
− ‚ąí -->
sin
‚Ā° -->
x
,
{\displaystyle (\cos x)'=-\sin x\,,}
(
tg
‚Ā° -->
x
)
′
=
1
cos
2
‚Ā° -->
x
=
1
+
tg
2
‚Ā° -->
x
=
sec
2
‚Ā° -->
x
,
{\displaystyle (\operatorname {tg} x)'={\frac {1}{\cos ^{2}x}}=1+\operatorname {tg} ^{2}x=\sec ^{2}x,}
(
ctg
‚Ā° -->
x
)
′
=
− ‚ąí -->
1
sin
2
‚Ā° -->
x
=
− ‚ąí -->
cosec
2
‚Ā° -->
x
,
{\displaystyle (\operatorname {ctg} x)'=-{\frac {1}{\sin ^{2}x}}=-\operatorname {cosec} ^{2}x,}
(
sec
‚Ā° -->
x
)
′
=
sin
‚Ā° -->
x
cos
2
‚Ā° -->
x
=
sec
‚Ā° -->
x
tg
‚Ā° -->
x
,
{\displaystyle (\sec x)'={\frac {\sin x}{\cos ^{2}x}}=\sec x\operatorname {tg} x,}
(
cosec
‚Ā° -->
x
)
′
=
− ‚ąí -->
cos
‚Ā° -->
x
sin
2
‚Ā° -->
x
.
{\displaystyle (\operatorname {cosec} ~x)'=-{\frac {\cos x}{\sin ^{2}x}}.}
–ė–Ĺ—ā–Ķ–≥—Ä–į–Ľ—č —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ĺ–į –ĺ–Ī–Ľ–į—Ā—ā–ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –≤—č—Ä–į–∂–į—é—ā—Ā—Ź —á–Ķ—Ä–Ķ–∑ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ[ 7]
∫ ‚ąę -->
sin
‚Ā° -->
x
d
x
=
− ‚ąí -->
cos
‚Ā° -->
x
+
C
,
{\displaystyle \int \sin x\,dx=-\cos x+C\,,}
∫ ‚ąę -->
cos
‚Ā° -->
x
d
x
=
sin
‚Ā° -->
x
+
C
,
{\displaystyle \int \cos x\,dx=\sin x+C\,,}
∫ ‚ąę -->
tg
‚Ā° -->
x
d
x
=
− ‚ąí -->
ln
‚Ā° -->
|
cos
‚Ā° -->
x
|
+
C
,
{\displaystyle \int \operatorname {tg} x\,dx=-\ln \left|\cos x\right|+C\,,}
∫ ‚ąę -->
ctg
‚Ā° -->
x
d
x
=
ln
‚Ā° -->
|
sin
‚Ā° -->
x
|
+
C
,
{\displaystyle \int \operatorname {ctg} x\,dx=\ln \left|\sin x\right|+C\,,}
∫ ‚ąę -->
sec
‚Ā° -->
x
d
x
=
ln
‚Ā° -->
|
tg
(
π ŌÄ -->
4
+
x
2
)
|
+
C
,
{\displaystyle \int \sec x\,dx=\ln \left|\operatorname {tg} \,\left({\frac {\pi }{4}}+{\frac {x}{2}}\right)\right|+C\,,}
∫ ‚ąę -->
cosec
‚Ā° -->
x
d
x
=
ln
‚Ā° -->
|
tg
x
2
|
+
C
.
{\displaystyle \int \operatorname {cosec} ~x\,dx=\ln \left|\operatorname {tg} \,{\frac {x}{2}}\right|+C.}
–§–ĺ—Ä–ľ—É–Ľ–į –≠–Ļ–Ľ–Ķ—Ä–į :
e
i
ϑ ŌĎ -->
=
cos
‚Ā° -->
ϑ ŌĎ -->
+
i
sin
‚Ā° -->
ϑ ŌĎ -->
.
{\displaystyle e^{i\vartheta }=\cos \vartheta +i\sin \vartheta .}
–§–ĺ—Ä–ľ—É–Ľ–į –≠–Ļ–Ľ–Ķ—Ä–į –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ĺ—ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–ĺ–≤ —á–Ķ—Ä–Ķ–∑ —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā—É –Ņ–ĺ –į–Ĺ–į–Ľ–ĺ–≥–ł–ł —Ā –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł , –ł–Ľ–ł (—Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é —Ä—Ź–ī–ĺ–≤ ) –ļ–į–ļ –į–Ĺ–į–Ľ–ł—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–Ķ–Ĺ–ł–Ķ –ł—Ö –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö –į–Ĺ–į–Ľ–ĺ–≥–ĺ–≤:
sin
‚Ā° -->
z
=
∑ ‚ąĎ -->
n
=
0
∞ ‚ąě -->
(
− ‚ąí -->
1
)
n
(
2
n
+
1
)
!
z
2
n
+
1
=
e
i
z
− ‚ąí -->
e
− ‚ąí -->
i
z
2
i
=
sh
‚Ā° -->
i
z
i
;
{\displaystyle \sin z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}z^{2n+1}={\frac {e^{iz}-e^{-iz}}{2i}}\,={\frac {\operatorname {sh} iz}{i}};}
cos
‚Ā° -->
z
=
∑ ‚ąĎ -->
n
=
0
∞ ‚ąě -->
(
− ‚ąí -->
1
)
n
(
2
n
)
!
z
2
n
=
e
i
z
+
e
− ‚ąí -->
i
z
2
=
ch
‚Ā° -->
i
z
;
{\displaystyle \cos z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}z^{2n}={\frac {e^{iz}+e^{-iz}}{2}}\,=\operatorname {ch} iz;}
tg
z
=
sin
‚Ā° -->
z
cos
‚Ā° -->
z
=
e
i
z
− ‚ąí -->
e
− ‚ąí -->
i
z
i
(
e
i
z
+
e
− ‚ąí -->
i
z
)
;
{\displaystyle \operatorname {tg} \,z={\frac {\sin z}{\cos z}}={\frac {e^{iz}-e^{-iz}}{i(e^{iz}+e^{-iz})}};}
ctg
z
=
cos
‚Ā° -->
z
sin
‚Ā° -->
z
=
i
(
e
i
z
+
e
− ‚ąí -->
i
z
)
e
i
z
− ‚ąí -->
e
− ‚ąí -->
i
z
;
{\displaystyle \operatorname {ctg} \,z={\frac {\cos z}{\sin z}}={\frac {i(e^{iz}+e^{-iz})}{e^{iz}-e^{-iz}}};}
sec
‚Ā° -->
z
=
1
cos
‚Ā° -->
z
=
2
e
i
z
+
e
− ‚ąí -->
i
z
;
{\displaystyle \sec z={\frac {1}{\cos z}}={\frac {2}{e^{iz}+e^{-iz}}};}
cosec
z
=
1
sin
‚Ā° -->
z
=
2
i
e
i
z
− ‚ąí -->
e
− ‚ąí -->
i
z
,
{\displaystyle \operatorname {cosec} \,z={\frac {1}{\sin z}}={\frac {2i}{e^{iz}-e^{-iz}}},}
i
2
=
− ‚ąí -->
1.
{\displaystyle i^{2}=-1.}
x :
cos
‚Ā° -->
x
=
Re
‚Ā° -->
(
e
i
x
)
,
{\displaystyle \cos x=\operatorname {Re} (e^{ix}),}
sin
‚Ā° -->
x
=
Im
‚Ā° -->
(
e
i
x
)
.
{\displaystyle \sin x=\operatorname {Im} (e^{ix}).}
–ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–Ķ —Ā–ł–Ĺ—É—Ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā —ā–Ķ—Ā–Ĺ–ĺ —Ā–≤—Ź–∑–į–Ĺ—č —Ā –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł :
sin
‚Ā° -->
(
x
+
i
y
)
=
sin
‚Ā° -->
x
ch
y
+
i
cos
‚Ā° -->
x
sh
y
,
{\displaystyle \sin(x+iy)=\sin x\,\operatorname {ch} \,y+i\cos x\,\operatorname {sh} \,y,}
cos
‚Ā° -->
(
x
+
i
y
)
=
cos
‚Ā° -->
x
ch
y
− ‚ąí -->
i
sin
‚Ā° -->
x
sh
y
.
{\displaystyle \cos(x+iy)=\cos x\,\operatorname {ch} \,y-i\sin x\,\operatorname {sh} \,y.}
–Ď–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–ĺ –Ņ–Ķ—Ä–Ķ—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č—Ö –≤—č—ą–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —Ā–ĺ—Ö—Ä–į–Ĺ—Ź—é—ā—Ā—Ź –ł –≤ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ. –Ě–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į:
–ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–Ķ —Ā–ł–Ĺ—É—Ā –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā, –≤ –ĺ—ā–Ľ–ł—á–ł–Ķ –ĺ—ā –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö, –ľ–ĺ–≥—É—ā –Ņ—Ä–ł–Ĺ–ł–ľ–į—ā—Ć —Ā–ļ–ĺ–Ľ—Ć —É–≥–ĺ–ī–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ł–Ķ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ—é –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź;
–≤—Ā–Ķ –Ĺ—É–Ľ–ł –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —Ā–ł–Ĺ—É—Ā–į –ł –ļ–ĺ—Ā–ł–Ĺ—É—Ā–į –Ľ–Ķ–∂–į—ā –Ĺ–į –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –ĺ—Ā–ł.
–Ě–į —Ā–Ľ–Ķ–ī—É—é—Č–ł—Ö –≥—Ä–į—Ą–ł–ļ–į—Ö –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—Ź –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć, –į –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ļ –≤—č–ī–Ķ–Ľ–Ķ–Ĺ—č —Ü–≤–Ķ—ā–ĺ–ľ. –Į—Ä–ļ–ĺ—Ā—ā—Ć –ĺ—ā—Ä–į–∂–į–Ķ—ā –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ (—á—Ď—Ä–Ĺ—č–Ļ ‚ÄĒ –Ĺ–ĺ–Ľ—Ć). –¶–≤–Ķ—ā –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –ĺ—ā –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į –ł —É–≥–Ľ–į —Ā–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –ļ–į—Ä—ā–Ķ .
–Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –≤ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł
sin
z
{\displaystyle \sin \,z}
cos
z
{\displaystyle \cos \,z}
tg
z
{\displaystyle \operatorname {tg} \,z}
ctg
z
{\displaystyle \operatorname {ctg} \,z}
sec
z
{\displaystyle \sec \,z}
cosec
z
{\displaystyle \operatorname {cosec} \,z}
–õ–ł–Ĺ–ł—Ź —Ā–ł–Ĺ—É—Ā–į
O
y
B
=
x
B
B
{\displaystyle Oy_{B}=x_{B}B}
—Ö–ĺ—Ä–ī—č –ī–į–Ĺ–Ĺ–ĺ–Ļ –ī—É–≥–ł, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ī—É–≥–į —Ā —Ö–ĺ—Ä–ī–ĺ–Ļ –Ĺ–į–Ņ–ĺ–ľ–ł–Ĺ–į–Ķ—ā –Ľ—É–ļ —Ā —ā–Ķ—ā–ł–≤–ĺ–Ļ ). –ó–į—ā–Ķ–ľ —Ā–Ľ–ĺ–≤–ĺ ¬ę–į—Ä—Ö–į¬Ľ –Ī—č–Ľ–ĺ –ĺ—ā–Ī—Ä–ĺ—ą–Ķ–Ĺ–ĺ –ł –Ľ–ł–Ĺ–ł—é —Ā–ł–Ĺ—É—Ā–į —Ā—ā–į–Ľ–ł –Ĺ–į–∑—č–≤–į—ā—Ć –Ņ—Ä–ĺ—Ā—ā–ĺ ¬ę–ī–∂–ł–≤–į¬Ľ. –ź—Ä–į–Ī—Ā–ļ–ł–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł, –Ņ–Ķ—Ä–Ķ–≤–ĺ–ī—Ź –ł–Ĺ–ī–ł–Ļ—Ā–ļ–ł–Ķ –ļ–Ĺ–ł–≥–ł —Ā —Ā–į–Ĺ—Ā–ļ—Ä–ł—ā–į , –Ĺ–Ķ –Ņ–Ķ—Ä–Ķ–≤–Ķ–Ľ–ł —Ā–Ľ–ĺ–≤–ĺ ¬ę–ī–∂–ł–≤–į¬Ľ –į—Ä–į–Ī—Ā–ļ–ł–ľ —Ā–Ľ–ĺ–≤–ĺ–ľ ¬ę–≤–į—ā–į—ĬĽ, –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—Č–ł–ľ —ā–Ķ—ā–ł–≤—É –ł —Ö–ĺ—Ä–ī—É, –į —ā—Ä–į–Ĺ—Ā–ļ—Ä–ł–Ī–ł—Ä–ĺ–≤–į–Ľ–ł –Ķ–≥–ĺ –į—Ä–į–Ī—Ā–ļ–ł–ľ–ł –Ī—É–ļ–≤–į–ľ–ł –ł —Ā—ā–į–Ľ–ł –Ĺ–į–∑—č–≤–į—ā—Ć –Ľ–ł–Ĺ–ł—é —Ā–ł–Ĺ—É—Ā–į ¬ę–ī–∂–ł–Ī–į¬Ľ (ō¨Ŕäō® ). –Ę–į–ļ –ļ–į–ļ –≤ –į—Ä–į–Ī—Ā–ļ–ĺ–ľ —Ź–∑—č–ļ–Ķ –ļ—Ä–į—ā–ļ–ł–Ķ –≥–Ľ–į—Ā–Ĺ—č–Ķ –Ĺ–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—ā—Ā—Ź, –į –ī–ĺ–Ľ–≥–ĺ–Ķ ¬ę–ł¬Ľ –≤ —Ā–Ľ–ĺ–≤–Ķ ¬ę–ī–∂–ł–Ī–į¬Ľ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź —ā–į–ļ –∂–Ķ, –ļ–į–ļ –Ņ–ĺ–Ľ—É–≥–Ľ–į—Ā–Ĺ–į—Ź ¬ę–Ļ¬Ľ, –į—Ä–į–Ī—č —Ā—ā–į–Ľ–ł –Ņ—Ä–ĺ–ł–∑–Ĺ–ĺ—Ā–ł—ā—Ć –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ –Ľ–ł–Ĺ–ł–ł —Ā–ł–Ĺ—É—Ā–į –ļ–į–ļ ¬ę–ī–∂–į–Ļ–Ī¬Ľ, —á—ā–ĺ –Ī—É–ļ–≤–į–Ľ—Ć–Ĺ–ĺ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā ¬ę–≤–Ņ–į–ī–ł–Ĺ–į¬Ľ, ¬ę–Ņ–į–∑—É—Ö–į¬Ľ. –ü—Ä–ł –Ņ–Ķ—Ä–Ķ–≤–ĺ–ī–Ķ –į—Ä–į–Ī—Ā–ļ–ł—Ö —Ā–ĺ—á–ł–Ĺ–Ķ–Ĺ–ł–Ļ –Ĺ–į –Ľ–į—ā—č–Ĺ—Ć –Ķ–≤—Ä–ĺ–Ņ–Ķ–Ļ—Ā–ļ–ł–Ķ –Ņ–Ķ—Ä–Ķ–≤–ĺ–ī—á–ł–ļ–ł –Ņ–Ķ—Ä–Ķ–≤–Ķ–Ľ–ł —Ā–Ľ–ĺ–≤–ĺ ¬ę–ī–∂–į–Ļ–Ī¬Ľ –Ľ–į—ā–ł–Ĺ—Ā–ļ–ł–ľ —Ā–Ľ–ĺ–≤–ĺ–ľ sinus ‚ÄĒ ¬ę—Ā–ł–Ĺ—É—Ā¬Ľ, –ł–ľ–Ķ—é—Č–ł–ľ —ā–ĺ –∂–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ (–ł–ľ–Ķ–Ĺ–Ĺ–ĺ –≤ —ć—ā–ĺ–ľ –∑–Ĺ–į—á–Ķ–Ĺ–ł–ł –ĺ–Ĺ–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –ļ–į–ļ –į–Ĺ–į—ā–ĺ–ľ–ł—á–Ķ—Ā–ļ–ł–Ļ —ā–Ķ—Ä–ľ–ł–Ĺ —Ā–ł–Ĺ—É—Ā –Ľ–į—ā. cosinus ) ‚ÄĒ —ć—ā–ĺ —Ā–ĺ–ļ—Ä–į—Č–Ķ–Ĺ–ł–Ķ –ĺ—ā –Ľ–į—ā. complementi sinus ‚ÄĒ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ļ —Ā–ł–Ĺ—É—Ā. –õ–ł–Ĺ–ł—Ź –ļ–ĺ—Ā–ł–Ĺ—É—Ā–į
O
x
B
=
y
B
B
{\displaystyle Ox_{B}=y_{B}B}
–°–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ķ –ļ—Ä–į—ā–ļ–ł–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
–£–ł–Ľ—Ć—Ź–ľ–ĺ–ľ –ě—ā—Ä–Ķ–ī–ĺ–ľ –ł –Ď–ĺ–Ĺ–į–≤–Ķ–Ĺ—ā—É—Ä–ĺ–Ļ –ö–į–≤–į–Ľ—Ć–Ķ—Ä–ł –ł –∑–į–ļ—Ä–Ķ–Ņ–Ľ–Ķ–Ĺ—č –≤ —ā—Ä—É–ī–į—Ö –õ–Ķ–ĺ–Ĺ–į—Ä–ī–į –≠–Ļ–Ľ–Ķ—Ä–į .
–Ę–Ķ—Ä–ľ–ł–Ĺ—č ¬ę—ā–į–Ĺ–≥–Ķ–Ĺ—Ā¬Ľ (–Ľ–į—ā. tangens ‚ÄĒ –ļ–į—Ā–į—é—Č–ł–Ļ—Ā—Ź) –ł ¬ę—Ā–Ķ–ļ–į–Ĺ—Ā¬Ľ (–Ľ–į—ā. secans ‚ÄĒ —Ā–Ķ–ļ—É—Č–ł–Ļ) –Ī—č–Ľ–ł –≤–≤–Ķ–ī–Ķ–Ĺ—č –ī–į—ā—Ā–ļ–ł–ľ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ĺ–ľ –Ę–ĺ–ľ–į—Ā–ĺ–ľ –§–ł–Ĺ–ļ–Ķ –≤ –Ķ–≥–ĺ –ļ–Ĺ–ł–≥–Ķ ¬ę–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –ļ—Ä—É–≥–Ľ–ĺ–≥–嬼 (Geometria rotundi, 1583). –°–į–ľ —ā–Ķ—Ä–ľ–ł–Ĺ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –≤–≤–Ķ–ī—Ď–Ĺ –ö–Ľ—é–≥–Ķ–Ľ–Ķ–ľ –≤ 1770 –≥–ĺ–ī—É. –í XVIII –≤–Ķ–ļ–Ķ –Ė. –õ–į–≥—Ä–į–Ĺ–∂–Ķ–ľ –ł –ī—Ä—É–≥–ł–ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į–ľ–ł –Ī—č–Ľ–ł –≤–≤–Ķ–ī–Ķ–Ĺ—č –ł —ā–Ķ—Ä–ľ–ł–Ĺ—č –ī–Ľ—Ź –ĺ–Ī—Ä–į—ā–Ĺ—č—Ö —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ ‚ÄĒ –į—Ä–ļ—Ā–ł–Ĺ—É—Ā, –į—Ä–ļ–ļ–ĺ—Ā–ł–Ĺ—É—Ā, –į—Ä–ļ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā, –į—Ä–ļ–ļ–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā, –į—Ä–ļ—Ā–Ķ–ļ–į–Ĺ—Ā, –į—Ä–ļ–ļ–ĺ—Ā–Ķ–ļ–į–Ĺ—Ā ‚ÄĒ —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ī–ĺ–Ī–į–≤–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ł—Ā—ā–į–≤–ļ–ł ¬ę–į—Ä–ļ¬Ľ (–ĺ—ā –Ľ–į—ā. arcus ‚ÄĒ –ī—É–≥–į).
–í —ā–ł–Ņ–ĺ–≥—Ä–į—Ą–ł–ļ–Ķ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä—č –Ĺ–į —Ä–į–∑–Ĺ—č—Ö —Ź–∑—č–ļ–į—Ö —Ā–ĺ–ļ—Ä–į—Č—Ď–Ĺ–Ĺ–ĺ–Ķ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —Ä–į–∑–Ľ–ł—á–Ĺ–ĺ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –≤ –į–Ĺ–≥–Ľ–ĺ—Ź–∑—č—á–Ĺ–ĺ–Ļ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–Ķ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā, –ļ–ĺ—ā–į–Ĺ–≥–Ķ–Ĺ—Ā –ł –ļ–ĺ—Ā–Ķ–ļ–į–Ĺ—Ā –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—ā—Ā—Ź
tan
‚Ā° -->
x
{\displaystyle \tan x}
cot
‚Ā° -->
x
{\displaystyle \cot x}
csc
‚Ā° -->
x
{\displaystyle \csc x}
[ 8]
–ú–Ķ–∂–ī—É–Ĺ–į—Ä–ĺ–ī–Ĺ—č–Ļ —Ā—ā–į–Ĺ–ī–į—Ä—ā ISO 80000-2 ¬ęQuantities and units ‚ÄĒ Part 2: Mathematical signs and symbols to be used in the natural sciences and technology¬Ľ –Ņ—Ä–Ķ–ī–Ņ–ł—Ā—č–≤–į–Ķ—ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć —ā–ĺ–Ľ—Ć–ļ–ĺ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź
tan
‚Ā° -->
x
{\displaystyle \tan x}
cot
‚Ā° -->
x
{\displaystyle \cot x}
csc
‚Ā° -->
x
{\displaystyle \csc x}
–†–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–ł–Ļ –ď–ě–°–Ę –† 54521-2011 ¬ę–°—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –ľ–Ķ—ā–ĺ–ī—č. –ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–ł–ľ–≤–ĺ–Ľ—č –ł –∑–Ĺ–į–ļ–ł –ī–Ľ—Ź –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –≤ —Ā—ā–į–Ĺ–ī–į—Ä—ā–į—Ö¬Ľ —ā–į–ļ–∂–Ķ —Ä–Ķ–ļ–ĺ–ľ–Ķ–Ĺ–ī—É–Ķ—ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć
tan
‚Ā° -->
x
{\displaystyle \tan x}
cot
‚Ā° -->
x
{\displaystyle \cot x}
csc
‚Ā° -->
x
{\displaystyle \csc x}
t
g
x
{\displaystyle \mathrm {tg} x}
c
t
g
x
{\displaystyle \mathrm {ctg} x}
c
o
s
e
c
x
{\displaystyle \mathrm {cosec} x}
‚ÜĎ –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ: –ö–ĺ—Ä–Ĺ –ď., –ö–ĺ—Ä–Ĺ –Ę. –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ (–ī–Ľ—Ź –Ĺ–į—É—á–Ĺ—č—Ö —Ä–į–Ī–ĺ—ā–Ĺ–ł–ļ–ĺ–≤ –ł –ł–Ĺ–∂–Ķ–Ĺ–Ķ—Ä–ĺ–≤) . ‚ÄĒ –ú. : –Ě–į—É–ļ–į, 1973. ‚ÄĒ 720 —Ā. –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 19 —Ź–Ĺ–≤–į—Ä—Ź 2015 –≥–ĺ–ī–į.—Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č–ľ —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ .
‚ÜĎ –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ –Ņ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ, 1978 , —Ā. 282‚ÄĒ284.‚ÜĎ –®–į—Ö–ľ–Ķ–Ļ—Ā—ā–Ķ—Ä –ź. –•. –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č—Ö —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ // –Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—Ź : [—Ä—É—Ā. –ú. : –ė–∑–ī–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ –ú–¶–Ě–ú–ě ; –°–ü–Ī. : ¬ę–ü–Ķ—ā—Ä–ĺ–≥–Ľ–ł—Ą¬Ľ : ¬ę–í–ł–ļ—ā–ĺ—Ä–ł—Ź –Ņ–Ľ—é—Ā¬Ľ, 2013. ‚ÄĒ –°. 11, 14, 18, 20. ‚ÄĒ 752 —Ā. : –ł–Ľ–Ľ. ‚ÄĒ (–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į. –≠–Ľ–Ķ–ļ—ā–ł–≤–Ĺ—č–Ķ –ļ—É—Ä—Ā—č). ‚ÄĒ 1500 —ć–ļ–∑. ‚ÄĒ –Ď–Ď–ö 22.141—Ź71.6 . ‚ÄĒ –£–Ē–ö 373.167.1:512(G) ISBN 978-5-4439-0050-6 . ‚ÄĒ ISBN 978-5-98712-042-2 . ‚ÄĒ ISBN 978-5-91673-097-5 .‚ÜĎ –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ –Ņ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ, 1978 , —Ā. 271‚ÄĒ272.‚ÜĎ –õ–į—ā–ł–Ĺ—Ā–ļ–ĺ-—Ä—É—Ā—Ā–ļ–ł–Ļ —Ā–Ľ–ĺ–≤–į—Ä—Ć (–Ĺ–Ķ–ĺ–Ņ—Ä.) . –Ē–į—ā–į –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź: 9 –į–Ņ—Ä–Ķ–Ľ—Ź 2023. –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 9 –į–Ņ—Ä–Ķ–Ľ—Ź 2023 –≥–ĺ–ī–į.‚ÜĎ –ė–Ľ—Ć–ł–Ĺ –í. –ź. , –ü–ĺ–∑–Ĺ—Ź–ļ –≠. –ď. –ú. : –Ě–į—É–ļ–į , 1998. ‚ÄĒ ISBN 5-02-015231-5 .‚ÜĎ –í —Ą–ĺ—Ä–ľ—É–Ľ–į—Ö, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł—Ö –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ –≤ –Ņ—Ä–į–≤–ĺ–Ļ —á–į—Ā—ā–ł —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤, –ļ–ĺ–Ĺ—Ā—ā–į–Ĺ—ā—č –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź
C
{\displaystyle \scriptstyle C}
‚ÜĎ –ó–Ĺ–į–ļ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ļ. // –Ď–ĺ–Ľ—Ć—ą–į—Ź —Ā–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź . 1-–Ķ –ł–∑–ī. –Ę. 27. ‚ÄĒ –ú., 1933.
–Ď–Ķ—Ä–ľ–į–Ĺ—ā –ź. –§., –õ—é—Ā—ā–Ķ—Ä–Ĺ–ł–ļ –õ. –ź. –Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—Ź. ‚ÄĒ –ú.: –Ě–į—É–ļ–į, 1967.–Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł ‚ÄĒ —Ā—ā–į—ā—Ć—Ź –ł–∑ –Ď–ĺ–Ľ—Ć—ą–ĺ–Ļ —Ā–ĺ–≤–Ķ—ā—Ā–ļ–ĺ–Ļ —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł–ł . . –Ę. 26. ‚ÄĒ –ú.: –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź , 1977. ‚ÄĒ –°. 204‚ÄĒ206.–Ď—Ä–ĺ–Ĺ—ą—ā–Ķ–Ļ–Ĺ –ė. –Ě. , –°–Ķ–ľ–Ķ–Ĺ–ī—Ź–Ķ–≤ –ö. –ź. –ü—Ä—Ź–ľ–ĺ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–į—Ź —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—Ź // –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ . ‚ÄĒ –ė–∑–ī. 7-–Ķ, —Ā—ā–Ķ—Ä–Ķ–ĺ—ā–ł–Ņ–Ĺ–ĺ–Ķ. ‚ÄĒ –ú. : –ď–ĺ—Ā—É–ī–į—Ä—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ķ –ł–∑–ī–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ —ā–Ķ—Ö–Ĺ–ł–ļ–ĺ-—ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä—č, 1967. ‚ÄĒ –°. 179‚ÄĒ184.–í—č–≥–ĺ–ī—Ā–ļ–ł–Ļ –ú. –Į. –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ –Ņ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ . ‚ÄĒ –ú. : –Ě–į—É–ļ–į, 1978.–Ē–≤–į–Ļ—ā –ď. –Ď. –Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł // –Ę–į–Ī–Ľ–ł—Ü—č –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ĺ–≤ –ł –ī—Ä—É–≥–ł–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą–ĺ—Ä–ľ—É–Ľ—č. ‚ÄĒ 4-–Ķ –ł–∑–ī. ‚ÄĒ –ú. : –Ě–į—É–ļ–į, 1973. ‚ÄĒ –°. 70‚ÄĒ102.–ö–ĺ–∂–Ķ—É—Ä–ĺ–≤ –ü. –ź . –Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—Ź. ‚ÄĒ –ú.: –§–ł–∑–ľ–į—ā–≥–ł–∑, 1963.–ú–į—Ä–ļ—É—ą–Ķ–≤–ł—á –ź. –ė . –ó–į–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ā–ł–Ĺ—É—Ā—č. ‚ÄĒ –ú.: –Ě–į—É–ļ–į, 1974.–Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł // –ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź . ‚ÄĒ –ú.: –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, 1984.
–Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł // –≠–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–Ľ–ĺ–≤–į—Ä—Ć —é–Ĺ–ĺ–≥–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į. ‚ÄĒ –ú.: –ü–Ķ–ī–į–≥–ĺ–≥–ł–ļ–į , 1985. ‚ÄĒ –°. 299‚ÄĒ301‚ÄĒ305. ‚ÄĒ 352 —Ā. ‚ÄĒ ISBN 5-7155-0218-7 /
–Ę—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł // –°–Ņ—Ä–į–≤–ĺ—á–Ĺ–ł–ļ –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ (–ī–Ľ—Ź —Ā—Ä. —É—á. –∑–į–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ) / –¶—č–Ņ–ļ–ł–Ĺ –ź. –ď., –Ņ–ĺ–ī —Ä–Ķ–ī. –°—ā–Ķ–Ņ–į–Ĺ–ĺ–≤–į –°. –ź. ‚ÄĒ 3-–Ķ –ł–∑–ī. ‚ÄĒ –ú.: –Ě–į—É–ļ–į, –ď–Ľ. —Ä–Ķ–ī–į–ļ—Ü–ł—Ź —Ą–ł–∑.-–ľ–į—ā. –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä—č, 1983. ‚ÄĒ –°. 240‚ÄĒ258. ‚ÄĒ 480 —Ā.
–°—Ā—č–Ľ–ļ–ł –Ĺ–į –≤–Ĺ–Ķ—ą–Ĺ–ł–Ķ —Ä–Ķ—Ā—É—Ä—Ā—č
–Ę–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–į–Ļ—ā—č
–°–Ľ–ĺ–≤–į—Ä–ł –ł —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł–ł
–í –Ī–ł–Ī–Ľ–ł–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–į—ā–į–Ľ–ĺ–≥–į—Ö













































































































































































































































































































































![{\displaystyle \sin(n\alpha )=\sum _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\cos ^{n-2k-1}\alpha \,\sin ^{2k+1}\alpha ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb020e5dfc3b2d5dfe1d1a0c571487ce387a8153)
![{\displaystyle \cos(n\alpha )=\sum _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\cos ^{n-2k}\alpha \,\sin ^{2k}\alpha ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84f285d7cb530e87d8a9e33cff84fd4a4c9a8205)
![{\displaystyle \mathrm {tg} (n\alpha )={\frac {\sin(n\alpha )}{\cos(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {tg} ^{2k+1}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {tg} ^{2k}\alpha }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8800a20a70495802fc2de287bb98d155e14720b1)
![{\displaystyle \mathrm {ctg} (n\alpha )={\frac {\cos(n\alpha )}{\sin(n\alpha )}}={\dfrac {\displaystyle {\sum \limits _{k=0}^{[n/2]}(-1)^{k}{\binom {n}{2k}}\mathrm {ctg} ^{n-2k}\alpha }}{\displaystyle {\sum \limits _{k=0}^{[(n-1)/2]}(-1)^{k}{\binom {n}{2k+1}}\mathrm {ctg} ^{n-2k-1}\alpha }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90744f04ee2a1e34b1f0763e310c1c1d071f240d)
![{\displaystyle [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26847bfc29bbeb4d6ef62ac3fd076378c0fd1db)