–£ —ć—ā–ĺ–≥–ĺ —ā–Ķ—Ä–ľ–ł–Ĺ–į —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –ł –ī—Ä—É–≥–ł–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź, —Ā–ľ.
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź .
–Ē–į–Ĺ–Ĺ–į—Ź —Ā—ā–į—ā—Ć—Ź –ĺ–Ņ–ł—Ā—č–≤–į–Ķ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ. –ě –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —Ā–ľ. –ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–Ļ –į–Ĺ–į–Ľ–ł–∑ .–ė–Ľ–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –ü—Ä–ĺ–ł–∑–≤–ĺŐĀ–ī–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł ‚ÄĒ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ł—Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź , —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—é—Č–Ķ–Ķ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł –≤ –ī–į–Ĺ–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ. –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–į–ļ –Ņ—Ä–Ķ–ī–Ķ–Ľ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź –Ņ—Ä–ł—Ä–į—Č–Ķ–Ĺ–ł—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł –ļ –Ņ—Ä–ł—Ä–į—Č–Ķ–Ĺ–ł—é –Ķ—Ď –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į –Ņ—Ä–ł —Ā—ā—Ä–Ķ–ľ–Ľ–Ķ–Ĺ–ł–ł –Ņ—Ä–ł—Ä–į—Č–Ķ–Ĺ–ł—Ź –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į –ļ –Ĺ—É–Ľ—é (–Ņ—Ä–ł —É—Ā–Ľ–ĺ–≤–ł–ł, —á—ā–ĺ —ā–į–ļ–ĺ–Ļ –Ņ—Ä–Ķ–ī–Ķ–Ľ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā). –§—É–Ĺ–ļ—Ü–ł—é, –ł–ľ–Ķ—é—Č—É—é –ļ–ĺ–Ĺ–Ķ—á–Ĺ—É—é –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é (–≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —ā–ĺ—á–ļ–Ķ), –Ĺ–į–∑—č–≤–į—é—ā –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä—É–Ķ–ľ–ĺ–Ļ (–≤ –ī–į–Ĺ–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ).
–ü—Ä–ĺ—Ü–Ķ—Ā—Ā –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–łŐĀ—Ä–ĺ–≤–į–Ĺ–ł–Ķ–ľ .
–ě–Ī—Ä–į—ā–Ĺ—č–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā ‚ÄĒ –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł–Ķ –Ņ–Ķ—Ä–≤–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–ĺ–Ļ ‚ÄĒ –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ .
–í –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ĺ–ľ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–ľ –ł—Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —á–į—Č–Ķ –≤—Ā–Ķ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź —á–Ķ—Ä–Ķ–∑ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ –Ņ—Ä–Ķ–ī–Ķ–Ľ–į , –ĺ–ī–Ĺ–į–ļ–ĺ –ł—Ā—ā–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł —ā–Ķ–ĺ—Ä–ł—Ź –Ņ—Ä–Ķ–ī–Ķ–Ľ–ĺ–≤ –Ņ–ĺ—Ź–≤–ł–Ľ–į—Ā—Ć –Ņ–ĺ–∑–∂–Ķ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ł—Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź. –ė—Ā—ā–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –≤–≤–ĺ–ī–ł–Ľ–į—Ā—Ć –ļ–ł–Ĺ–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł (–ļ–į–ļ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć) –ł–Ľ–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł (–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—Ź—Ā—Ć –Ņ–ĺ —Ā—É—ā–ł –Ĺ–į–ļ–Ľ–ĺ–Ĺ–ĺ–ľ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, –≤ —Ä–į–∑–Ĺ—č—Ö –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ—č—Ö —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į—Ö). –Ě—Ć—é—ā–ĺ–Ĺ –Ĺ–į–∑—č–≤–į–Ľ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é —Ą–Ľ—é–ļ—Ā–ł–Ķ–Ļ , –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—Ź —ā–ĺ—á–ļ–ĺ–Ļ –Ĺ–į–ī —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ —Ą—É–Ĺ–ļ—Ü–ł–ł, —ą–ļ–ĺ–Ľ–į –õ–Ķ–Ļ–Ī–Ĺ–ł—Ü–į –Ņ—Ä–Ķ–ī–Ņ–ĺ—á–ł—ā–į–Ľ–į –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –Ī–į–∑–ĺ–≤–ĺ–≥–ĺ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ [ 1]
–†—É—Ā—Ā–ļ–ł–Ļ —ā–Ķ—Ä–ľ–ł–Ĺ –≤ —Ą–ĺ—Ä–ľ–Ķ ¬ę–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź¬Ľ –≤–Ņ–Ķ—Ä–≤—č–Ķ —É–Ņ–ĺ—ā—Ä–Ķ–Ī–ł–Ľ –í. –ė. –í–ł—Ā–ļ–ĺ–≤–į—ā–ĺ–≤ , –Ņ–Ķ—Ä–Ķ–≤–Ķ–ī—Ź –Ĺ–į —Ä—É—Ā—Ā–ļ–ł–Ļ —Ź–∑—č–ļ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ļ —Ą—Ä–į–Ĺ—Ü—É–∑—Ā–ļ–ł–Ļ —ā–Ķ—Ä–ľ–ł–Ĺ d√©riv√©e , –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—č–Ļ —Ą—Ä–į–Ĺ—Ü—É–∑—Ā–ļ–ł–ľ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ĺ–ľ –õ–į–≥—Ä–į–Ĺ–∂–Ķ–ľ [ 2]
–ü—É—Ā—ā—Ć –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ĺ–ļ—Ä–Ķ—Ā—ā–Ĺ–ĺ—Ā—ā–ł —ā–ĺ—á–ļ–ł
x
0
∈ ‚ąą -->
R
{\displaystyle x_{0}\in \mathbb {R} }
—Ą—É–Ĺ–ļ—Ü–ł—Ź
f
: : -->
U
(
x
0
)
⊂ ‚äā -->
R
→ ‚Üí -->
R
.
{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .}
A
{\displaystyle A}
U
(
x
0
)
{\displaystyle U(x_{0})}
f
(
x
0
+
h
)
=
f
(
x
0
)
+
A
h
+
o
(
h
)
,
h
→ ‚Üí -->
0
{\displaystyle f(x_{0}+h)=f(x_{0})+Ah+o(h),h\rightarrow 0}
–Ķ—Ā–Ľ–ł
A
{\displaystyle A}
–Ņ—Ä–Ķ–ī–Ķ–Ľ –ü—É—Ā—ā—Ć –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ĺ–ļ—Ä–Ķ—Ā—ā–Ĺ–ĺ—Ā—ā–ł —ā–ĺ—á–ļ–ł
x
0
∈ ‚ąą -->
R
{\displaystyle x_{0}\in \mathbb {R} }
—Ą—É–Ĺ–ļ—Ü–ł—Ź
f
: : -->
U
(
x
0
)
⊂ ‚äā -->
R
→ ‚Üí -->
R
.
{\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} .}
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
–Ņ—Ä–Ķ–ī–Ķ–Ľ , –Ķ—Ā–Ľ–ł –ĺ–Ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā,
f
′
(
x
0
)
=
lim
x
→ ‚Üí -->
x
0
f
(
x
)
− ‚ąí -->
f
(
x
0
)
x
− ‚ąí -->
x
0
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
f
(
x
0
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
0
)
Δ őĒ -->
x
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
Δ őĒ -->
f
(
x
)
Δ őĒ -->
x
.
{\displaystyle f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}}=\lim _{\Delta x\to 0}{\frac {f(x_{0}+\Delta x)-f(x_{0})}{\Delta x}}=\lim \limits _{{\Delta x}\to 0}{\frac {\Delta {f(x)}}{\Delta x}}.}
0
f
′
(
x
0
)
=
f
x
′
(
x
0
)
=
D
f
(
x
0
)
=
d
f
d
x
(
x
0
)
=
d
y
d
x
|
x
=
x
0
=
y
˙ ňô -->
(
x
0
)
.
{\displaystyle f'(x_{0})=f'_{x}(x_{0})=\mathrm {D} \!f(x_{0})={\frac {df}{dx}}(x_{0})=\left.{\frac {dy}{dx}}\right\vert _{x=x_{0}}={\dot {y}}(x_{0}).}
–ó–į–ľ–Ķ—ā–ł–ľ, —á—ā–ĺ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–Ķ–Ķ –ĺ–Ī—č—á–Ĺ–ĺ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –Ņ–ĺ –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł (–≤ —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ľ–Ķ—Ö–į–Ĺ–ł–ļ–Ķ –ł —Ą–ł–∑–ł–ļ–Ķ, –ł—Ā—ā–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł —á–į—Ā—ā–ĺ —ā–ĺ–∂–Ķ).
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ –ĺ–Ī—Ä–į—ā–Ĺ—č—Ö —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ
(
c
o
n
s
t
)
(
n
)
=
0
{\displaystyle \left(const\right)^{(n)}=0}
(
sin
‚Ā° -->
x
)
(
n
)
=
sin
‚Ā° -->
(
x
+
π ŌÄ -->
n
2
)
{\displaystyle \left(\sin x\right)^{(n)}=\sin(x+{\dfrac {\pi n}{2}})}
(
arcsin
‚Ā° -->
x
)
′
=
1
1
− ‚ąí -->
x
2
{\displaystyle \left(\arcsin x\right)'={\dfrac {1}{\sqrt {1-x^{2}}}}}
(
sinh
‚Ā° -->
x
)
′
=
cosh
‚Ā° -->
x
{\displaystyle (\sinh x)'=\cosh x}
(
x
a
)
(
n
)
=
a
!
(
a
− ‚ąí -->
n
)
!
x
a
− ‚ąí -->
n
{\displaystyle \left(x^{a}\right)^{(n)}={\dfrac {a!}{(a-n)!}}x^{a-n}}
(
cos
‚Ā° -->
x
)
(
n
)
=
− ‚ąí -->
s
i
n
(
x
+
π ŌÄ -->
n
2
)
{\displaystyle \left(\cos x\right)^{(n)}=-sin(x+{\dfrac {\pi n}{2}})}
(
arccos
‚Ā° -->
x
)
′
=
− ‚ąí -->
1
1
− ‚ąí -->
x
2
{\displaystyle \left(\arccos x\right)'=-{\dfrac {1}{\sqrt {1-x^{2}}}}}
(
cosh
‚Ā° -->
x
)
′
=
sinh
‚Ā° -->
x
{\textstyle (\cosh x)'=\sinh x}
(
a
x
)
(
n
)
=
a
x
ln
n
‚Ā° -->
a
{\displaystyle \left(a^{x}\right)^{(n)}=a^{x}\ln ^{n}a}
(
tg
‚Ā° -->
x
)
′
=
sec
2
‚Ā° -->
x
{\displaystyle \left(\operatorname {tg} x\right)'=\sec ^{2}x}
(
arctg
‚Ā° -->
x
)
′
=
1
1
+
x
2
{\displaystyle \left(\operatorname {arctg} x\right)'={\dfrac {1}{1+x^{2}}}}
(
tanh
‚Ā° -->
x
)
′
=
sch
2
‚Ā° -->
x
{\displaystyle (\tanh x)'=\operatorname {sch} ^{2}x}
(
e
x
)
(
n
)
=
e
x
{\displaystyle \left(e^{x}\right)^{\left(n\right)}=e^{x}}
(
ctg
‚Ā° -->
x
)
′
=
− ‚ąí -->
csc
2
‚Ā° -->
x
{\displaystyle \left(\operatorname {ctg} x\right)'=-\csc ^{2}x}
(
arcctg
‚Ā° -->
x
)
′
=
− ‚ąí -->
1
1
+
x
2
{\displaystyle \left(\operatorname {arcctg} x\right)'=-{\dfrac {1}{1+x^{2}}}}
(
coth
‚Ā° -->
x
)
′
=
− ‚ąí -->
csch
2
‚Ā° -->
x
{\displaystyle (\coth x)'=-\operatorname {csch} ^{2}x}
(
log
a
‚Ā° -->
x
)
(
n
)
=
(
− ‚ąí -->
1
)
n
− ‚ąí -->
1
(
n
− ‚ąí -->
1
)
!
x
n
ln
‚Ā° -->
a
{\displaystyle \left(\log _{a}x\right)^{(n)}={\dfrac {(-1)^{n-1}(n-1)!}{x^{n}\ln a}}}
(
sec
‚Ā° -->
x
)
′
=
sec
‚Ā° -->
x
⋅ ‚čÖ -->
t
g
x
{\displaystyle \left(\operatorname {sec} x\right)'=\sec x\cdot \mathrm {tg} \ x}
(
arcsec
‚Ā° -->
x
)
′
=
1
|
x
|
x
2
− ‚ąí -->
1
{\displaystyle \left(\operatorname {arcsec} x\right)'={\frac {1}{|x|{\sqrt {x^{2}-1}}}}}
(
s
c
h
x
)
′
=
− ‚ąí -->
sinh
‚Ā° -->
x
cosh
2
‚Ā° -->
x
{\displaystyle (\mathrm {sch} \ x)'=-{\frac {\sinh x}{\cosh ^{2}x}}}
(
ln
‚Ā° -->
x
)
(
n
)
=
(
− ‚ąí -->
1
)
n
− ‚ąí -->
1
(
n
− ‚ąí -->
1
)
!
x
n
{\displaystyle (\ln {x})^{(n)}={\dfrac {(-1)^{n-1}(n-1)!}{x^{n}}}}
(
cosec
‚Ā° -->
x
)
′
=
− ‚ąí -->
c
o
s
e
c
x
⋅ ‚čÖ -->
c
t
g
x
{\displaystyle \left(\operatorname {cosec} x\right)'=-\mathrm {cosec} \ x\cdot \mathrm {ctg} \ x}
(
arccosec
‚Ā° -->
x
)
′
=
− ‚ąí -->
1
|
x
|
x
2
− ‚ąí -->
1
{\displaystyle \left(\operatorname {arccosec} x\right)'=-{\frac {1}{|x|{\sqrt {x^{2}-1}}}}}
(
c
s
c
h
x
)
′
=
− ‚ąí -->
cosh
‚Ā° -->
x
sinh
2
‚Ā° -->
x
{\displaystyle (\mathrm {csch} \ x)'=-{\frac {\cosh x}{\sinh ^{2}x}}}
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź
f
′
(
x
0
)
{\displaystyle f'(x_{0})}
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
f
∈ ‚ąą -->
D
(
x
0
)
⇔ ‚áĒ -->
∃ ‚ąÉ -->
f
′
(
x
0
)
∈ ‚ąą -->
(
− ‚ąí -->
∞ ‚ąě -->
;
∞ ‚ąě -->
)
.
{\displaystyle f\in {\mathcal {D}}(x_{0})\Leftrightarrow \exists f'(x_{0})\in (-\infty ;\infty ).}
–Ē–Ľ—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä—É–Ķ–ľ–ĺ–Ļ –≤
x
0
{\displaystyle x_{0}}
f
{\displaystyle f}
U
(
x
0
)
{\displaystyle U(x_{0})}
f
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
− ‚ąí -->
x
0
)
+
o
(
x
− ‚ąí -->
x
0
)
{\displaystyle f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})}
x
→ ‚Üí -->
x
0
.
{\displaystyle x\to x_{0}.}
–Ě–į–∑–ĺ–≤—Ď–ľ
Δ őĒ -->
x
=
x
− ‚ąí -->
x
0
{\displaystyle \Delta x=x-x_{0}}
–Ņ—Ä–ł—Ä–į—Č–Ķ–Ĺ–ł–Ķ–ľ –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į —Ą—É–Ĺ–ļ—Ü–ł–ł, –į
Δ őĒ -->
y
=
f
(
x
)
− ‚ąí -->
f
(
x
0
)
{\displaystyle \Delta y=f(x)-f(x_{0})}
Δ őĒ -->
y
=
f
(
x
0
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
0
)
{\displaystyle \Delta y=f(x_{0}+\Delta x)-f(x_{0})}
x
0
.
{\displaystyle x_{0}.}
f
′
(
x
0
)
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
Δ őĒ -->
f
Δ őĒ -->
x
.
{\displaystyle f'(x_{0})=\lim \limits _{\Delta x\to 0}{\frac {\Delta f}{\Delta x}}.}
–ü—É—Ā—ā—Ć —Ą—É–Ĺ–ļ—Ü–ł—Ź
f
: : -->
(
a
,
b
)
→ ‚Üí -->
R
{\displaystyle f\colon (a,b)\to \mathbb {R} }
x
0
∈ ‚ąą -->
(
a
,
b
)
.
{\displaystyle x_{0}\in (a,b).}
–Ņ—Ä–ĺ–ł–∑–≤–ĺŐĀ–ī–Ĺ–į—Ź —Ą—ÉŐĀ–Ĺ–ļ—Ü–ł—Ź
f
′
: : -->
(
a
,
b
)
→ ‚Üí -->
R
.
{\displaystyle f'\colon (a,b)\to \mathbb {R} .}
–§—É–Ĺ–ļ—Ü–ł—Ź, –ł–ľ–Ķ—é—Č–į—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –≤ —ā–ĺ—á–ļ–Ķ, –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–į –≤ –Ĺ–Ķ–Ļ. –ě–Ī—Ä–į—ā–Ĺ–ĺ–Ķ –Ĺ–Ķ –≤—Ā–Ķ–≥–ī–į –≤–Ķ—Ä–Ĺ–ĺ.
–ē—Ā–Ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź —Ā–į–ľ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ļ, —ā–ĺ —Ą—É–Ĺ–ļ—Ü–ł—é
f
{\displaystyle f}
–Ĺ–Ķ–Ņ—Ä–Ķ—Ä—čŐĀ–≤–Ĺ–ĺ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–łŐĀ—Ä—É–Ķ–ľ–ĺ–Ļ –ł –Ņ–ł—ą—É—ā:
f
∈ ‚ąą -->
C
(
1
)
(
(
a
,
b
)
)
.
{\displaystyle f\in C^{(1)}{\bigl (}(a,b){\bigr )}.}
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ. –Ě–į –≥—Ä–į—Ą–ł–ļ–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –≤—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź –į–Ī—Ā—Ü–ł—Ā—Ā–į x0 –ł –≤—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–į—Ź –ĺ—Ä–ī–ł–Ĺ–į—ā–į f(x0 ) . –í –ĺ–ļ—Ä–Ķ—Ā—ā–Ĺ–ĺ—Ā—ā–ł —ā–ĺ—á–ļ–ł x0 –≤—č–Ī–ł—Ä–į–Ķ—ā—Ā—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–į—Ź —ā–ĺ—á–ļ–į x . –ß–Ķ—Ä–Ķ–∑ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –≥—Ä–į—Ą–ł–ļ–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł F –Ņ—Ä–ĺ–≤–ĺ–ī–ł—ā—Ā—Ź —Ā–Ķ–ļ—É—Č–į—Ź (–Ņ–Ķ—Ä–≤–į—Ź —Ā–≤–Ķ—ā–Ľ–ĺ-—Ā–Ķ—Ä–į—Ź –Ľ–ł–Ĺ–ł—Ź C5 ). –†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ őĒx = x ‚ÄĒ x0 —É—Ā—ā—Ä–Ķ–ľ–Ľ—Ź–Ķ—ā—Ā—Ź –ļ –Ĺ—É–Ľ—é, –≤ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–Ķ —Ā–Ķ–ļ—É—Č–į—Ź –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –≤ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—É—é (–Ņ–ĺ—Ā—ā–Ķ–Ņ–Ķ–Ĺ–Ĺ–ĺ —ā–Ķ–ľ–Ĺ–Ķ—é—Č–ł–Ķ –Ľ–ł–Ĺ–ł–ł C5 ‚ÄĒ C1 ). –Ę–į–Ĺ–≥–Ķ–Ĺ—Ā —É–≥–Ľ–į őĪ –Ĺ–į–ļ–Ľ–ĺ–Ĺ–į —ć—ā–ĺ–Ļ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ ‚ÄĒ –ł –Ķ—Ā—ā—Ć –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –≤ —ā–ĺ—á–ļ–Ķ x0 . –ē—Ā–Ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź
f
: : -->
U
(
x
0
)
→ ‚Üí -->
R
{\displaystyle f\colon U(x_{0})\to \mathbb {R} }
x
0
,
{\displaystyle x_{0},}
U
(
x
0
)
{\displaystyle U(x_{0})}
–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ
f
l
(
x
)
≡ ‚Č° -->
f
(
x
0
)
+
f
′
(
x
0
)
(
x
− ‚ąí -->
x
0
)
.
{\displaystyle f_{l}(x)\equiv f(x_{0})+f'(x_{0})(x-x_{0}).}
–§—É–Ĺ–ļ—Ü–ł—Ź
f
l
{\displaystyle f_{l}}
f
{\displaystyle f}
x
0
.
{\displaystyle x_{0}.}
f
′
(
x
0
)
{\displaystyle f'(x_{0})}
—É–≥–Ľ–ĺ–≤—č–ľ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–ĺ–ľ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–ĺ–ľ —É–≥–Ľ–į –Ĺ–į–ļ–Ľ–ĺ–Ĺ–į –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ.
–Ę–į–Ĺ–≥–Ķ–Ĺ—Ā –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –ľ–į—Ā—ą—ā–į–Ī–ł—Ä—É—é—Č–ł–Ļ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –ł–Ľ–ł –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź: –Ĺ–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –ĺ—Ä–ī–ł–Ĺ–į—ā—č –Ī–ĺ–Ľ—Ć—ą–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –į–Ī—Ā—Ü–ł—Ā—Ā—č. –ē—Ā–Ľ–ł —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —Ä–į–≤–Ķ–Ĺ 1, —ā–ĺ –∑–į–≤–ł—Ā–ł–ľ–ĺ–Ķ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ĺ–į—Ā—ā–ĺ–Ľ—Ć–ļ–ĺ –∂–Ķ, –Ĺ–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ–Ķ. –ē—Ā–Ľ–ł —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —Ä–į–≤–Ķ–Ĺ –Ĺ—É–Ľ—é, –∑–Ĺ–į—á–ł—ā –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ĺ–Ķ –Ņ—Ä–ł–≤–ĺ–ī–ł—ā –ļ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—é –∑–į–≤–ł—Ā–ł–ľ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ.
–ė–∑–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ (–≤ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö –∑–į–ī–į—á–į—Ö) —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–Ķ–∑—Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ (–ī–Ľ–ł–Ĺ–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ľ–Ķ–∂–į—Č–Ķ–≥–ĺ –ļ–į—ā–Ķ—ā–į ‚ąē –ī–Ľ–ł–Ĺ–į –Ņ—Ä–ł–Ľ–Ķ–∂–į—Č–Ķ–≥–ĺ –ļ–į—ā–Ķ—ā–į, –ľ‚ąē–ľ), –Ĺ–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ļ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—é –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ —ā–į–Ĺ–≥–Ķ–Ĺ—Ā –ľ–ĺ–∂–Ķ—ā –ł–ľ–Ķ—ā—Ć —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć —ā–Ķ–Ľ–į –Ķ—Ā—ā—Ć –Ņ—É—ā—Ć‚ąē–≤—Ä–Ķ–ľ—Ź, —ā. –Ķ. –ľ‚ąē—Ā.
–ü—É—Ā—ā—Ć
s
=
s
(
t
)
{\displaystyle s=s(t)}
–ī–≤–ł–∂–Ķ–Ĺ–ł—Ź . –Ę–ĺ–≥–ī–į
v
(
t
0
)
=
s
′
(
t
0
)
{\displaystyle v(t_{0})=s'(t_{0})}
–ľ–≥–Ĺ–ĺ–≤–Ķ–Ĺ–Ĺ—É—é —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł
t
0
{\displaystyle t_{0}}
s
′
(
t
)
{\displaystyle s'(t)}
s
″
(
t
)
{\displaystyle s''(t)}
a
(
t
0
)
=
s
″
(
t
0
)
{\displaystyle a(t_{0})=s''(t_{0})}
–ľ–≥–Ĺ–ĺ–≤–Ķ–Ĺ–Ĺ–ĺ–Ķ —É—Ā–ļ–ĺ—Ä–Ķ–Ĺ–ł–Ķ –≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł
t
0
.
{\displaystyle t_{0}.}
–í–ĺ–ĺ–Ī—Č–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł
y
=
f
(
x
)
{\displaystyle y=f(x)}
x
0
{\displaystyle x_{0}}
x
0
{\displaystyle x_{0}}
–Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į , –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā—Ć—é
y
=
f
(
x
)
.
{\displaystyle y=f(x).}
–ü—Ä–ł –Ņ—Ä–ĺ—ā–Ķ–ļ–į–Ĺ–ł–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ (—Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł—Ö, –ľ–Ķ—Ö–į–Ĺ–ł—á–Ķ—Ā–ļ–ł—Ö, —Ö–ł–ľ–ł—á–Ķ—Ā–ļ–ł—Ö, —ć–ļ–ĺ–Ĺ–ĺ–ľ–ł—á–Ķ—Ā–ļ–ł—Ö –ł —ā. –Ņ.) –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā –∑–į–≤–ł—Ā–ł—ā –Ĺ–Ķ —ā–ĺ–Ľ—Ć–ļ–ĺ –ĺ—ā –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤, –Ĺ–ĺ –ł –ĺ—ā —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —ć—ā–ł—Ö –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ (–≤–Ņ–Ľ–ĺ—ā—Ć –ī–ĺ –ļ–į—á–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź). –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ—Ä–ł –ľ–Ķ–ī–Ľ–Ķ–Ĺ–Ĺ–ĺ–ľ –≤—Ä–į—Č–Ķ–Ĺ–ł–ł —Ä–ĺ—ā–ĺ—Ä–į –≥–Ķ–Ĺ–Ķ—Ä–į—ā–ĺ—Ä–į –Ĺ–į–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤—č—Ö–ĺ–ī–Ķ –Ī—É–ī–Ķ—ā –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ –ł –Ĺ–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ–ł—ā –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –Ķ–≥–ĺ –≤–ĺ –ľ–Ĺ–ĺ–≥–ł—Ö —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł—Ö –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź—Ö. –ü—Ä–ł –Ī—č—Ā—ā—Ä–ĺ–ľ –≤—Ä–į—Č–Ķ–Ĺ–ł–ł —ā–ĺ–≥–ĺ –∂–Ķ —Ä–ĺ—ā–ĺ—Ä–į –Ĺ–į–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł–Ķ —É–≤–Ķ–Ľ–ł—á–ł–≤–į–Ķ—ā—Ā—Ź; –Ņ–ĺ–ľ–ł–ľ–ĺ —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ł—Ź —Ā—Ą–Ķ—Ä—č –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł—Ź –ĺ–Ĺ–ĺ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ĺ–į—á–ł–Ĺ–į–Ķ—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—ā—Ć –ĺ–Ņ–į—Ā–Ĺ–ĺ—Ā—ā—Ć –ī–Ľ—Ź –Ņ–Ķ—Ä—Ā–ĺ–Ĺ–į–Ľ–į. –ü—Ä–ł –Ķ—Č–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ–Ļ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —Ä–ĺ—ā–ĺ—Ä–į –Ĺ–į–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł–Ķ —É–≤–Ķ–Ľ–ł—á–ł–≤–į–Ķ—ā—Ā—Ź –Ĺ–į—Ā—ā–ĺ–Ľ—Ć–ļ–ĺ, —á—ā–ĺ –ľ–ĺ–∂–Ķ—ā –Ņ–ĺ–≤—Ä–Ķ–ī–ł—ā—Ć –ł–∑–ĺ–Ľ—Ź—Ü–ł—é –Ņ—Ä–ĺ–≤–ĺ–ī–ĺ–≤, –≤—č–∑–≤–į—ā—Ć –ļ–ĺ—Ä–ĺ–Ĺ–Ĺ—č–Ļ —Ä–į–∑—Ä—Ź–ī, –≤—č–≤–Ķ—Ā—ā–ł –ł–∑ —Ā—ā—Ä–ĺ—Ź –Ņ–ĺ–ī–ļ–Ľ—é—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –ĺ–Ī–ĺ—Ä—É–ī–ĺ–≤–į–Ĺ–ł–Ķ –ł —ā. –Ņ. –í —ć—ā–ĺ–ľ —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤–į–∂–Ĺ–ĺ—Ā—ā—Ć –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –ĺ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤.
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—ā—Ć –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é —Ą—É–Ĺ–ļ—Ü–ł–ł –ļ–į–ļ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł –≤ –ī–į–Ĺ–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ –Ĺ–Ķ –≤—Ā–Ķ–≥–ī–į –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–Ĺ–ĺ, —ā–į–ļ –ļ–į–ļ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć - —ć—ā–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –ļ–į–ļ–ĺ–Ļ-—ā–ĺ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł –ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā—č–ľ —Ā–Ľ—É—á–į–Ķ–ľ –Ņ—Ä–ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –∑–į–ī–į—á –Ĺ–į –ī–≤–ł–∂–Ķ–Ĺ–ł–Ķ. –ē—Ā—ā—Ć –∑–į–ī–į—á–ł, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ –≤ —ā–Ķ—á–Ķ–Ĺ–ł–Ķ –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł, –į –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā –ī—Ä—É–≥–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č. –í –ļ—Ä–ł–≤–ĺ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł –≤—č—Ā–ĺ—ā–į –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā –ī–Ľ–ł–Ĺ—č –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź. –ö–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –Ņ—Ä–ĺ—Ä–Ķ–į–≥–ł—Ä–ĺ–≤–į–≤—ą–Ķ–≥–ĺ –≤–Ķ—Č–Ķ—Ā—ā–≤–į –≤ —Ö–ł–ľ–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –ļ–ĺ–Ĺ—Ü–Ķ–Ĺ—ā—Ä–į—Ü–ł–ł —Ä–Ķ–į–≥–Ķ–Ĺ—ā–ĺ–≤ –ł —ā.–Ņ. –í —ć—ā–ł—Ö —Ā–Ľ—É—á–į—Ź—Ö –ł–ľ–Ķ–Ķ—ā —Ā–ľ—č—Ā–Ľ –≥–ĺ–≤–ĺ—Ä–ł—ā—Ć –ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –Ĺ–Ķ –ļ–į–ļ –ĺ —Ā–ļ–ĺ—Ä–ĺ—Ā—ā–ł, –į –ļ–į–ļ –ĺ –≥—Ä–į—Ą–ł–ļ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ļ (–Ņ—Ä–ł—Ä–ĺ—Ā—ā–į –ł–Ľ–ł —É–Ī—č–Ľ–ł) –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā –ī—Ä—É–≥–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č.
–ü—Ä–ł –ĺ–Ņ–ł—Ā–į–Ĺ–ł–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –ł –≤ —ā–Ķ–ĺ—Ä–ł–ł —É–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—é—ā –ļ–į–ļ —Ä–Ķ–į–ļ—Ü–ł—é –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į (—Ą—É–Ĺ–ļ—Ü–ł–ł) –Ĺ–į —É–Ņ—Ä–į–≤–Ľ—Ź—é—Č–ł–Ļ —ć—ā–ł–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–ľ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä (–Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ–Ķ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ķ). –Ě–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ł–Ĺ—ā–Ķ–Ĺ—Ā–ł–≤–Ĺ–ĺ —Ä–Ķ–į–≥–ł—Ä—É–Ķ—ā –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā –Ĺ–į —É–Ņ—Ä–į–≤–Ľ—Ź—é—Č–ł–Ļ —Ā–ł–≥–Ĺ–į–Ľ (–Ĺ–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –ĺ–Ĺ —á—É–≤—Ā—ā–≤–ł—ā–Ķ–Ľ–Ķ–Ĺ –ļ –Ĺ–Ķ–ľ—É). –ö–į–ļ–ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į –≤—č–∑—č–≤–į–Ķ—ā –Ĺ–Ķ–Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —É–Ņ—Ä–į–≤–Ľ—Ź—é—Č–Ķ–≥–ĺ –≤–ĺ–∑–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź.
–í –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö –∑–į–ī–į—á–į—Ö –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ļ–į–ļ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ –≤—č—Ā–ĺ—ā—č –ļ—Ä–ł–≤–ĺ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł –Ĺ–į –ľ–į–Ľ–ĺ–ľ —É—á–į—Ā—ā–ļ–Ķ –Ķ–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź (–ļ—Ä–ł–≤–ĺ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ—É—é —ā—Ä–į–Ņ–Ķ—Ü–ł—é –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ —Ā –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –≤—č—Ā–ĺ—ā–ĺ–Ļ); –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —Ä–į–ī–ł—É—Ā–į —Ą–ł–≥—É—Ä—č –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź –Ĺ–į –ľ–į–Ľ–ĺ–ľ —É—á–į—Ā—ā–ļ–Ķ –Ķ–Ķ –ĺ—Ā–ł –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź (—Ą–ł–≥—É—Ä–į –≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ļ–į–ļ —Ü–ł–Ľ–ł–Ĺ–ī—Ä —Ā –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–ľ —Ä–į–ī–ł—É—Ā–ĺ–ľ) –ł —ā. –Ņ.
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –ľ–ĺ–∂–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –ļ–į–ļ –Ņ—Ä–Ķ–ī–ł–ļ—ā–ĺ—Ä (—É—Ā—ā—Ä–ĺ–Ļ—Ā—ā–≤–ĺ –ł–Ľ–ł –ľ–Ķ—ā–ĺ–ī, –Ņ—Ä–Ķ–ī—Ā–ļ–į–∑—č–≤–į—é—Č–ł–Ļ –Ī—É–ī—É—Č–Ķ–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į). –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł —Ā–Ņ—Ä–ĺ—Ā –Ĺ–į –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł—é —Ä–į—Ā—ā–Ķ—ā, —ā–ĺ –Ņ—Ä–ł—Ä–ĺ—Ā—ā —Ā–Ņ—Ä–ĺ—Ā–į —É–≤–Ķ–Ľ–ł—á–ł–≤–į–Ķ—ā—Ā—Ź, –≤ –Ī—É–ī—É—Č–Ķ–ľ –Ņ–ĺ—ā—Ä–Ķ–Ī–Ĺ–ĺ—Ā—ā—Ć –≤ –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł–ł –Ī—É–ī–Ķ—ā —ā–ĺ–Ľ—Ć–ļ–ĺ —Ä–į—Ā—ā–ł –ł –ł–ľ–Ķ–Ķ—ā —Ā–ľ—č—Ā–Ľ —Ä–į—Ā—ą–ł—Ä—Ź—ā—Ć –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–ĺ. –ē—Ā–Ľ–ł —Ā–Ņ—Ä–ĺ—Ā –Ĺ–į –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł—é –Ņ–į–ī–į–Ķ—ā, —ā–ĺ –Ņ—Ä–ł—Ä–ĺ—Ā—ā —Ā–Ņ—Ä–ĺ—Ā–į —É–ľ–Ķ–Ĺ—Ć—ą–į–Ķ—ā—Ā—Ź –ł –≤ –Ī—É–ī—É—Č–Ķ–ľ –Ņ—Ä–ĺ–ī—É–ļ—Ü–ł—Ź —Ā—ā–į–Ĺ–Ķ—ā –Ĺ–Ķ –≤–ĺ—Ā—ā—Ä–Ķ–Ī–ĺ–≤–į–Ĺ–į. –ė–ľ–Ķ–Ķ—ā —Ā–ľ—č—Ā–Ľ –∑–į–ļ—Ä—č–≤–į—ā—Ć –ł–Ľ–ł –Ņ–Ķ—Ä–Ķ–Ņ—Ä–ĺ—Ą–ł–Ľ–ł—Ä–ĺ–≤–į—ā—Ć –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–ĺ.
–í –ü–ė–Ē-—Ä–Ķ–≥—É–Ľ—Ź—ā–ĺ—Ä–į—Ö –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –Ņ—Ä–Ķ–ī–ł–ļ—ā–ĺ—Ä–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–į—Ź —Ā–ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–į—Ź: –Ķ—Ā–Ľ–ł —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ķ–Ĺ–ł—Ź –ĺ—ą–ł–Ī–ļ–ł –ļ –ĺ–Ņ–ĺ—Ä–Ĺ–ĺ–ľ—É —Ā–ł–≥–Ĺ–į–Ľ—É –Ĺ–Ķ–≤–Ķ–Ľ–ł–ļ–į, –ł–ľ–Ķ–Ķ—ā —Ā–ľ—č—Ā–Ľ —É–≤–Ķ–Ľ–ł—á–ł—ā—Ć —É–Ņ—Ä–į–≤–Ľ—Ź—é—Č–Ķ–Ķ –≤–ĺ–∑–ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ, —á—ā–ĺ–Ī—č —É—Ā–ļ–ĺ—Ä–ł—ā—Ć –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā —É–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź. –ē—Ā–Ľ–ł —Ā–ļ–ĺ—Ä–ĺ—Ā—ā—Ć –Ņ—Ä–ł–Ī–Ľ–ł–∂–Ķ–Ĺ–ł—Ź –ĺ—ą–ł–Ī–ļ–ł –≤–Ķ–Ľ–ł–ļ–į, —Ā–ł—Ā—ā–Ķ–ľ–į —É–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź —É–ľ–Ķ–Ĺ—Ć—ą–į–Ķ—ā —É–Ņ—Ä–į–≤–Ľ—Ź—é—Č–Ķ–Ķ –≤–ĺ–∑–ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ, —á—ā–ĺ–Ī—č –Ĺ–Ķ –Ņ—Ä–ĺ—Ā–ļ–ĺ—á–ł—ā—Ć –ĺ–Ņ–ĺ—Ä–Ĺ—č–Ļ —Ā–ł–≥–Ĺ–į–Ľ –Ņ–ĺ –ł–Ĺ–Ķ—Ä—Ü–ł–ł. –ź–Ĺ–ł–ľ–į—Ü–ł—Ź, –ī–į—é—Č–į—Ź –Ņ–Ķ—Ä–≤–ĺ–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–Ķ –ł–Ĺ—ā—É–ł—ā–ł–≤–Ĺ–ĺ–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ, –ļ–į–ļ –ĺ ¬ę—Ä–į–∑–ľ–į—Ö–Ķ¬Ľ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł –Ņ—Ä–ł –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–ł –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į (–Ĺ–į–∂–ľ–ł—ā–Ķ –ī–Ľ—Ź –≤–ĺ—Ā–Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź).
–ü–ĺ–Ĺ—Ź—ā–ł–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į –∑–į–ī–į—Ď—ā—Ā—Ź —Ä–Ķ–ļ—É—Ä—Ä–Ķ–Ĺ—ā–Ĺ–ĺ . –ü–ĺ–Ľ–į–≥–į–Ķ–ľ
f
(
0
)
(
x
0
)
≡ ‚Č° -->
f
(
x
0
)
.
{\displaystyle f^{(0)}(x_{0})\equiv f(x_{0}).}
–ē—Ā–Ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź
f
{\displaystyle f}
x
0
{\displaystyle x_{0}}
f
(
1
)
(
x
0
)
≡ ‚Č° -->
f
′
(
x
0
)
.
{\displaystyle f^{(1)}(x_{0})\equiv f'(x_{0}).}
–ü—É—Ā—ā—Ć —ā–Ķ–Ņ–Ķ—Ä—Ć –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź
n
{\displaystyle n}
f
(
n
)
{\displaystyle f^{(n)}}
x
0
{\displaystyle x_{0}}
f
(
n
+
1
)
(
x
0
)
=
(
f
(
n
)
)
′
(
x
0
)
.
{\displaystyle f^{(n+1)}(x_{0})=\left(f^{(n)}\right)'(x_{0}).}
–í —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –≤—ā–ĺ—Ä–į—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –ĺ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ:
f
″
(
x
0
)
=
(
f
′
(
x
)
)
′
|
x
=
x
0
{\displaystyle f''(x_{0})=(f'(x))'|_{x=x_{0}}}
–ē—Ā–Ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź
u
=
f
(
x
,
y
,
z
)
{\displaystyle u=f(x,y,z)}
—á–į—Ā—ā–Ĺ—É—é –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –Ņ–ĺ –ĺ–ī–Ĺ–ĺ–Ļ –ł–∑ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö, —ā–ĺ –Ĺ–į–∑–≤–į–Ĺ–Ĺ–į—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź, —Ā–į–ľ–į —Ź–≤–Ľ—Ź—Ź—Ā—Ć —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ –ĺ—ā
x
,
y
,
z
,
{\displaystyle x,y,z,}
(
x
0
,
y
0
,
z
0
)
{\displaystyle (x_{0},y_{0},z_{0})}
u
=
f
(
x
,
y
,
z
)
{\displaystyle u=f(x,y,z)}
u
x
2
″
=
f
x
2
″
(
x
0
,
y
0
,
z
0
)
{\displaystyle u''_{x^{2}}=f''_{x^{2}}(x_{0},y_{0},z_{0})}
∂ ‚ąā -->
2
u
∂ ‚ąā -->
x
2
=
∂ ‚ąā -->
2
f
(
x
0
,
y
0
,
z
0
)
∂ ‚ąā -->
x
2
{\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x^{2}}}}
u
x
y
″
=
f
x
y
″
(
x
0
,
y
0
,
z
0
)
{\displaystyle u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})}
∂ ‚ąā -->
2
u
∂ ‚ąā -->
x
∂ ‚ąā -->
y
=
∂ ‚ąā -->
2
f
(
x
0
,
y
0
,
z
0
)
∂ ‚ąā -->
x
∂ ‚ąā -->
y
{\displaystyle {\frac {\partial ^{2}u}{\partial x\partial y}}={\frac {\partial ^{2}f(x_{0},y_{0},z_{0})}{\partial x\partial y}}}
–ß–į—Ā—ā–Ĺ–į—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –ł–Ľ–ł –Ī–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į, –≤–∑—Ź—ā–į—Ź –Ņ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ—č–ľ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–ľ, –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —Ā–ľ–Ķ—ą–į–Ĺ–Ĺ–ĺ–Ļ —á–į—Ā—ā–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ . –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä,
u
x
y
″
=
f
x
y
″
(
x
0
,
y
0
,
z
0
)
{\displaystyle u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})}
–ö–Ľ–į—Ā—Ā —Ą—É–Ĺ–ļ—Ü–ł–Ļ, —É –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź
n
{\displaystyle n}
C
(
n
)
{\displaystyle C^{(n)}}
–í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā —Ü–Ķ–Ľ–Ķ–Ļ, –ĺ–Ī–Ľ–į—Ā—ā–ł –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ–ĺ–≥–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –į–Ņ–Ņ–į—Ä–į—ā–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ —Ā–Ņ–ĺ—Ā–ĺ–Ī—č –∑–į–Ņ–ł—Ā–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö. –Ę–į–ļ, –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź n-–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –∑–į–Ņ–ł—Ā–į–Ĺ–į –≤ –Ĺ–ĺ—ā–į—Ü–ł—Ź—Ö:
f
(
1
)
(
x
0
)
=
f
′
(
x
0
)
=
f
I
(
x
0
)
,
{\displaystyle f^{(1)}(x_{0})=f'(x_{0})=f^{I}(x_{0}),}
f
(
2
)
(
x
0
)
=
f
″
(
x
0
)
=
f
I
I
(
x
0
)
,
{\displaystyle f^{(2)}(x_{0})=f''(x_{0})=f^{II}(x_{0}),}
f
(
3
)
(
x
0
)
=
f
‴
(
x
0
)
=
f
I
I
I
(
x
0
)
,
{\displaystyle f^{(3)}(x_{0})=f'''(x_{0})=f^{III}(x_{0}),}
f
(
4
)
(
x
0
)
=
f
I
V
(
x
0
)
,
{\displaystyle f^{(4)}(x_{0})=f^{IV}(x_{0}),}
–Ę–į–ļ–į—Ź –∑–į–Ņ–ł—Ā—Ć —É–ī–ĺ–Ī–Ĺ–į —Ā–≤–ĺ–Ķ–Ļ –ļ—Ä–į—ā–ļ–ĺ—Ā—ā—Ć—é –ł —ą–ł—Ä–ĺ–ļ–ĺ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–į; –ĺ–ī–Ĺ–į–ļ–ĺ —ą—ā—Ä–ł—Ö–į–ľ–ł —Ä–į–∑—Ä–Ķ—ą–į–Ķ—ā—Ā—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—ā—Ć –Ĺ–Ķ –≤—č—ą–Ķ —ā—Ä–Ķ—ā—Ć–Ķ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ.
–õ–Ķ–Ļ–Ī–Ĺ–ł—Ü–į , —É–ī–ĺ–Ī–Ĺ–į—Ź –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ–Ļ –∑–į–Ņ–ł—Ā—Ć—é –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ľ–į–Ľ—č—Ö (—ā–ĺ–Ľ—Ć–ļ–ĺ –≤ —Ā–Ľ—É—á–į–Ķ, –Ķ—Ā–Ľ–ł
x
{\displaystyle x}
d
n
f
d
x
n
(
x
0
)
{\displaystyle {\frac {d^{n}\!f}{dx^{n}}}(x_{0})}
–Ě—Ć—é—ā–ĺ–Ĺ–į , –ļ–ĺ—ā–ĺ—Ä–į—Ź —á–į—Ā—ā–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –≤ –ľ–Ķ—Ö–į–Ĺ–ł–ļ–Ķ –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –Ņ–ĺ –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł —Ą—É–Ĺ–ļ—Ü–ł–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č (–ī–Ľ—Ź –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ —á–į—Č–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā –∑–į–Ņ–ł—Ā—Ć –õ–į–≥—Ä–į–Ĺ–∂–į). –ü–ĺ—Ä—Ź–ī–ĺ–ļ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā—Ā—Ź —á–ł—Ā–Ľ–ĺ–ľ —ā–ĺ—á–Ķ–ļ –Ĺ–į–ī —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä:
x
˙ ňô -->
(
t
0
)
{\displaystyle {\dot {x}}(t_{0})}
x
{\displaystyle x}
t
{\displaystyle t}
t
=
t
0
{\displaystyle t=t_{0}}
f
¨ ¬® -->
(
x
0
)
{\displaystyle {\ddot {f}}(x_{0})}
f
{\displaystyle f}
x
{\displaystyle x}
x
0
{\displaystyle x_{0}}
D
n
f
(
x
0
)
{\displaystyle \mathrm {D} ^{n}\!f(x_{0})}
∂ ‚ąā -->
n
f
(
x
0
)
{\displaystyle \partial ^{n}\!f(x_{0})}
–í –≤–į—Ä–ł–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–ľ –ł—Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł–ł –ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–Ķ —á–į—Ā—ā–ĺ –Ņ—Ä–ł–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ
f
x
{\displaystyle f_{x}}
f
x
x
{\displaystyle f_{xx}}
f
x
|
x
=
x
0
{\displaystyle f_{x}\vert _{x=x_{0}}}
–ö–ĺ–Ĺ–Ķ—á–Ĺ–ĺ, –Ņ—Ä–ł —ć—ā–ĺ–ľ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ĺ–Ķ –∑–į–Ī—č–≤–į—ā—Ć, —á—ā–ĺ —Ā–Ľ—É–∂–į—ā –≤—Ā–Ķ –ĺ–Ĺ–ł –ī–Ľ—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ĺ–ī–Ĺ–ł—Ö –ł —ā–Ķ—Ö –∂–Ķ –ĺ–Ī—ä–Ķ–ļ—ā–ĺ–≤:
f
(
n
)
(
x
0
)
=
d
n
f
d
x
n
(
x
0
)
=
f
⋅ ‚čÖ -->
⋅ ‚čÖ -->
… ‚Ķ -->
⋅ ‚čÖ -->
⏞ ‚Źě -->
n
раз
(
x
0
)
=
D
n
f
(
x
0
)
=
f
x
x
… ‚Ķ -->
x
⏟ ‚Źü -->
n
раз
|
x
=
x
0
.
{\displaystyle f^{(n)}(x_{0})={\frac {d^{n}\!f}{dx^{n}}}(x_{0})={\overset {\overbrace {\cdot \cdot \ldots \cdot } ^{n\ {\text{—Ä–į–∑}}}}{f}}(x_{0})=\mathrm {D} ^{n}\!f(x_{0})=f{\underbrace {_{xx\ldots x}} _{n\ {\text{—Ä–į–∑}}}}\vert _{x=x_{0}}.}
–ü—É—Ā—ā—Ć
f
(
x
)
=
x
2
{\displaystyle f(x)=x^{2}}
f
′
(
x
0
)
=
lim
x
→ ‚Üí -->
x
0
x
2
− ‚ąí -->
x
0
2
x
− ‚ąí -->
x
0
=
lim
x
→ ‚Üí -->
x
0
(
x
− ‚ąí -->
x
0
)
(
x
+
x
0
)
x
− ‚ąí -->
x
0
=
lim
x
→ ‚Üí -->
x
0
(
x
+
x
0
)
=
2
x
0
.
{\displaystyle f'(x_{0})=\lim \limits _{x\to x_{0}}{\frac {x^{2}-x_{0}^{2}}{x-x_{0}}}=\lim \limits _{x\to x_{0}}{\frac {(x-x_{0})(x+x_{0})}{x-x_{0}}}=\lim \limits _{x\to x_{0}}(x+x_{0})=2x_{0}.}
–ü—É—Ā—ā—Ć
f
(
x
)
=
|
x
|
{\displaystyle f(x)=|x|}
x
0
≠ ‚Ȇ -->
0
,
{\displaystyle x_{0}\neq 0,}
f
′
(
x
0
)
=
sgn
‚Ā° -->
x
0
,
{\displaystyle f'(x_{0})=\operatorname {sgn} x_{0},}
–≥–ī–Ķ
sgn
{\displaystyle \operatorname {sgn} }
—Ą—É–Ĺ–ļ—Ü–ł—é –∑–Ĺ–į–ļ–į . –ź –Ķ—Ā–Ľ–ł
x
0
=
0
,
{\displaystyle x_{0}=0,}
f
+
′
(
x
0
)
=
1
,
f
− ‚ąí -->
′
(
x
0
)
=
− ‚ąí -->
1
,
{\displaystyle f'_{+}(x_{0})=1,\;f'_{-}(x_{0})=-1,}
f
′
(
x
0
)
{\displaystyle f'(x_{0})}
–Ē–Ľ—Ź –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ
f
,
g
{\displaystyle f,g}
[
a
,
b
]
{\displaystyle [a,b]}
(
a
,
b
)
{\displaystyle (a,b)}
–õ–Ķ–ľ–ľ–į –§–Ķ—Ä–ľ–į .
f
{\displaystyle f}
c
{\displaystyle c}
f
′
(
c
)
{\displaystyle f'(c)}
f
′
(
c
)
=
0
{\displaystyle f'(c)=0}
–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ –Ĺ—É–Ľ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ .
f
{\displaystyle f}
[
a
,
b
]
{\displaystyle [a,b]}
(
a
,
b
)
{\displaystyle (a,b)}
–§–ĺ—Ä–ľ—É–Ľ–į –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö –Ņ—Ä–ł—Ä–į—Č–Ķ–Ĺ–ł–Ļ .
f
{\displaystyle f}
c
∈ ‚ąą -->
(
a
,
b
)
{\displaystyle c\in (a,b)}
f
(
b
)
− ‚ąí -->
f
(
a
)
b
− ‚ąí -->
a
=
f
′
(
c
)
{\displaystyle {\frac {f(b)-f(a)}{b-a}}=f'(c)}
–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ö–ĺ—ą–ł –ĺ —Ā—Ä–Ķ–ī–Ĺ–Ķ–ľ –∑–Ĺ–į—á–Ķ–Ĺ–ł–ł .
g
′
{\displaystyle g'}
(
a
,
b
)
{\displaystyle (a,b)}
c
∈ ‚ąą -->
(
a
,
b
)
{\displaystyle c\in (a,b)}
f
(
b
)
− ‚ąí -->
f
(
a
)
g
(
b
)
− ‚ąí -->
g
(
a
)
=
f
′
(
c
)
g
′
(
c
)
{\displaystyle {\frac {f(b)-f(a)}{g(b)-g(a)}}={\frac {f'(c)}{g'(c)}}}
–ü—Ä–į–≤–ł–Ľ–ĺ –õ–ĺ–Ņ–ł—ā–į–Ľ—Ź .
lim
x
→ ‚Üí -->
c
f
(
x
)
=
lim
x
→ ‚Üí -->
c
g
(
x
)
=
0
{\displaystyle \lim _{x\to c}f(x)=\lim _{x\to c}g(x)=0}
∞ ‚ąě -->
{\displaystyle \infty }
g
′
(
x
)
≠ ‚Ȇ -->
0
{\displaystyle g'(x)\neq 0}
x
{\displaystyle x}
c
{\displaystyle c}
lim
x
→ ‚Üí -->
c
f
′
(
x
)
g
′
(
x
)
{\displaystyle \lim _{x\to c}{\frac {f'(x)}{g'(x)}}}
lim
x
→ ‚Üí -->
c
f
(
x
)
g
(
x
)
=
lim
x
→ ‚Üí -->
c
f
′
(
x
)
g
′
(
x
)
{\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}}
–ě–Ņ–Ķ—Ä–į—Ü–ł—Ź –Ĺ–į—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ–ľ. –ü—Ä–ł –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–ł —ć—ā–ĺ–Ļ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —á–į—Ā—ā–ĺ –Ņ—Ä–ł—Ö–ĺ–ī–ł—ā—Ā—Ź —Ä–į–Ī–ĺ—ā–į—ā—Ć —Ā —á–į—Ā—ā–Ĺ—č–ľ–ł, —Ā—É–ľ–ľ–į–ľ–ł, –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ, –į —ā–į–ļ–∂–Ķ —Ā ¬ę—Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ¬Ľ, —ā–ĺ –Ķ—Ā—ā—Ć —Ā–Ľ–ĺ–∂–Ĺ—č–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł. –ė—Ā—Ö–ĺ–ī—Ź –ł–∑ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ, –ľ–ĺ–∂–Ĺ–ĺ –≤—č–≤–Ķ—Ā—ā–ł –Ņ—Ä–į–≤–ł–Ľ–į –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź, –ĺ–Ī–Ľ–Ķ–≥—á–į—é—Č–ł–Ķ —ć—ā—É —Ä–į–Ī–ĺ—ā—É.
–ē—Ā–Ľ–ł
C
{\displaystyle C}
f
=
f
(
x
)
,
g
=
g
(
x
)
{\displaystyle f=f(x),g=g(x)}
–Ņ—Ä–į–≤–ł–Ľ–į –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź:
C
′
=
0
{\displaystyle C'=0}
x
′
=
1
{\displaystyle x'=1}
(
f
+
g
)
′
=
f
′
+
g
′
{\displaystyle \left(f+g\right)'=f'+g'}
[ 3] –Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
y
(
x
)
=
f
(
x
)
+
g
(
x
)
{\displaystyle y(x)=f(x)+g(x)}
y
′
(
x
)
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
y
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
y
(
x
)
Δ őĒ -->
x
=
{\displaystyle y'(x)=\lim _{\Delta x\to 0}{\frac {y(x+\Delta {x})-y(x)}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
(
f
(
x
+
Δ őĒ -->
x
)
+
g
(
x
+
Δ őĒ -->
x
)
)
− ‚ąí -->
(
f
(
x
)
+
g
(
x
)
)
Δ őĒ -->
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {(f(x+\Delta {x})+g(x+\Delta {x}))-(f(x)+g(x))}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
(
f
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
)
Δ őĒ -->
x
+
g
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
g
(
x
)
Δ őĒ -->
x
)
=
{\displaystyle =\lim _{\Delta x\to 0}{({\frac {f(x+\Delta x)-f(x)}{\Delta x}}+{\frac {g(x+\Delta x)-g(x)}{\Delta x}})}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
f
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
)
Δ őĒ -->
x
+
lim
Δ őĒ -->
x
→ ‚Üí -->
0
g
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
g
(
x
)
Δ őĒ -->
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}+\lim _{\Delta x\to 0}{\frac {g(x+\Delta x)-g(x)}{\Delta x}}=}
=
f
′
(
x
)
+
g
′
(
x
)
{\displaystyle =f'(x)+g'(x)}
‚Ė†
(
f
g
)
′
=
f
′
g
+
f
g
′
{\displaystyle \left(fg\right)'=f'g+fg'}
[ 4] –Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
y
(
x
)
=
f
(
x
)
g
(
x
)
{\displaystyle y(x)=f(x)g(x)}
Δ őĒ -->
f
(
x
)
=
f
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
)
{\displaystyle \Delta f(x)=f(x+\Delta x)-f(x)}
Δ őĒ -->
g
(
x
)
=
g
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
g
(
x
)
{\displaystyle \Delta g(x)=g(x+\Delta x)-g(x)}
y
′
(
x
)
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
y
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
y
(
x
)
Δ őĒ -->
x
=
{\displaystyle y'(x)=\lim _{\Delta x\to 0}{\frac {y(x+\Delta x)-y(x)}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
f
(
x
+
Δ őĒ -->
x
)
g
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
)
g
(
x
)
Δ őĒ -->
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)g(x+\Delta x)-f(x)g(x)}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
(
f
(
x
)
+
Δ őĒ -->
f
(
x
)
)
(
g
(
x
)
+
Δ őĒ -->
g
(
x
)
)
− ‚ąí -->
f
(
x
)
g
(
x
)
Δ őĒ -->
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {(f(x)+\Delta f(x))(g(x)+\Delta g(x))-f(x)g(x)}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
f
(
x
)
g
(
x
)
+
f
(
x
)
Δ őĒ -->
g
(
x
)
+
Δ őĒ -->
f
(
x
)
g
(
x
)
+
Δ őĒ -->
f
(
x
)
Δ őĒ -->
g
(
x
)
− ‚ąí -->
f
(
x
)
g
(
x
)
Δ őĒ -->
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x)g(x)+f(x)\Delta g(x)+\Delta f(x)g(x)+\Delta f(x)\Delta g(x)-f(x)g(x)}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
(
f
(
x
)
Δ őĒ -->
g
(
x
)
Δ őĒ -->
x
+
g
(
x
)
Δ őĒ -->
f
(
x
)
Δ őĒ -->
x
+
Δ őĒ -->
g
(
x
)
Δ őĒ -->
f
(
x
)
Δ őĒ -->
x
)
=
{\displaystyle =\lim _{\Delta x\to 0}(f(x){\frac {\Delta g(x)}{\Delta x}}+g(x){\frac {\Delta f(x)}{\Delta x}}+\Delta g(x){\frac {\Delta f(x)}{\Delta x}})=}
=
f
(
x
)
g
′
(
x
)
+
g
(
x
)
f
′
(
x
)
+
0
f
′
(
x
)
=
{\displaystyle =f(x)g'(x)+g(x)f'(x)+0f'(x)=}
=
f
′
(
x
)
g
(
x
)
+
f
(
x
)
g
′
(
x
)
{\displaystyle =f'(x)g(x)+f(x)g'(x)}
‚Ė†
(
C
f
)
′
=
C
f
′
{\displaystyle \left(Cf\right)'=Cf'}
(
f
g
)
′
=
f
′
g
− ‚ąí -->
f
g
′
g
2
{\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-fg'}{g^{2}}}}
‚Ȇ 0)–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
y
(
x
)
=
f
(
x
)
g
(
x
)
{\displaystyle y(x)={\frac {f(x)}{g(x)}}}
Δ őĒ -->
f
(
x
)
=
f
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
)
{\displaystyle \Delta f(x)=f(x+\Delta x)-f(x)}
Δ őĒ -->
g
(
x
)
=
g
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
g
(
x
)
{\displaystyle \Delta g(x)=g(x+\Delta x)-g(x)}
y
′
(
x
)
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
y
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
y
(
x
)
Δ őĒ -->
x
=
{\displaystyle y'(x)=\lim _{\Delta x\to 0}{\frac {y(x+\Delta x)-y(x)}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
f
(
x
+
Δ őĒ -->
x
)
g
(
x
+
Δ őĒ -->
x
)
− ‚ąí -->
f
(
x
)
g
(
x
)
Δ őĒ -->
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {{\frac {f(x+\Delta x)}{g(x+\Delta x)}}-{\frac {f(x)}{g(x)}}}{\Delta x}}=}
=
lim
Δ őĒ -->
x
→ ‚Üí -->
0
f
(
x
+
Δ őĒ -->
x
)
g
(
x
)
− ‚ąí -->
f
(
x
)
g
(
x
+
Δ őĒ -->
x
)
g
(
x
+
Δ őĒ -->
x
)
g
(
x
)
Δ őĒ -->
x
=
{\displaystyle =\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)g(x)-f(x)g(x+\Delta x)}{g(x+\Delta x)g(x)\Delta x}}=}
=
1
g
2
(
x
)
lim
Δ őĒ -->
x
→ ‚Üí -->
0
(
f
(
x
)
+
Δ őĒ -->
f
(
x
)
)
g
(
x
)
− ‚ąí -->
f
(
x
)
(
g
(
x
)
+
Δ őĒ -->
g
(
x
)
)
Δ őĒ -->
x
=
{\displaystyle ={\frac {1}{g^{2}(x)}}\lim _{\Delta x\to 0}{\frac {(f(x)+\Delta f(x))g(x)-f(x)(g(x)+\Delta g(x))}{\Delta x}}=}
=
1
g
2
(
x
)
lim
Δ őĒ -->
x
→ ‚Üí -->
0
f
(
x
)
g
(
x
)
+
Δ őĒ -->
f
(
x
)
g
(
x
)
− ‚ąí -->
f
(
x
)
g
(
x
)
− ‚ąí -->
f
(
x
)
Δ őĒ -->
g
(
x
)
Δ őĒ -->
x
=
{\displaystyle ={\frac {1}{g^{2}(x)}}\lim _{\Delta x\to 0}{\frac {f(x)g(x)+\Delta f(x)g(x)-f(x)g(x)-f(x)\Delta g(x)}{\Delta x}}=}
=
1
g
2
(
x
)
lim
Δ őĒ -->
x
→ ‚Üí -->
0
(
g
(
x
)
Δ őĒ -->
f
(
x
)
Δ őĒ -->
x
− ‚ąí -->
f
(
x
)
Δ őĒ -->
g
(
x
)
Δ őĒ -->
x
)
=
{\displaystyle ={\frac {1}{g^{2}(x)}}\lim _{\Delta x\to 0}{(g(x){\frac {\Delta f(x)}{\Delta x}}-f(x){\frac {\Delta g(x)}{\Delta x}})}=}
=
1
g
2
(
x
)
(
g
(
x
)
f
′
(
x
)
− ‚ąí -->
f
(
x
)
g
′
(
x
)
)
=
{\displaystyle ={\frac {1}{g^{2}(x)}}(g(x)f'(x)-f(x)g'(x))=}
=
f
′
(
x
)
g
(
x
)
− ‚ąí -->
f
(
x
)
g
′
(
x
)
g
2
(
x
)
{\displaystyle ={\frac {f'(x)g(x)-f(x)g'(x)}{g^{2}(x)}}}
‚Ė†
(
C
g
)
′
=
− ‚ąí -->
C
g
′
g
2
{\displaystyle \left({\frac {C}{g}}\right)'=-{\frac {Cg'}{g^{2}}}}
‚Ȇ 0)–ē—Ā–Ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź –∑–į–ī–į–Ĺ–į –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł:
{
x
=
x
(
t
)
,
y
=
y
(
t
)
,
t
∈ ‚ąą -->
[
T
1
;
T
2
]
{\displaystyle \left\{{\begin{matrix}x=x(t),\\y=y(t),\end{matrix}}\;\;t\in \left[T_{1};T_{2}\right]\right.}
y
x
′
=
d
y
d
x
=
d
y
d
t
⋅ ‚čÖ -->
d
t
d
x
=
y
t
′
⋅ ‚čÖ -->
t
x
′
=
y
t
′
x
t
′
{\displaystyle y'_{x}={\frac {dy}{dx}}={\frac {dy}{dt}}\cdot {\frac {dt}{dx}}=y'_{t}\cdot t'_{x}={\frac {y'_{t}}{x'_{t}}}}
d
d
x
f
(
g
(
x
)
)
=
d
f
(
g
)
d
g
⋅ ‚čÖ -->
d
g
(
x
)
d
x
=
f
g
′
g
x
′
{\displaystyle {\frac {d}{dx}}f(g(x))={\frac {df(g)}{dg}}\cdot {\frac {dg(x)}{dx}}=f'_{g}g'_{x}}
–§–ĺ—Ä–ľ—É–Ľ—č –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –ł –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź –ĺ–Ī–ĺ–Ī—Č–į—é—ā—Ā—Ź –Ĺ–į —Ā–Ľ—É—á–į–Ļ n-–ļ—Ä–į—ā–Ĺ–ĺ–≥–ĺ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź (—Ą–ĺ—Ä–ľ—É–Ľ–į –õ–Ķ–Ļ–Ī–Ĺ–ł—Ü–į ):
(
f
g
)
(
n
)
=
∑ ‚ąĎ -->
k
=
0
n
C
n
k
f
(
n
− ‚ąí -->
k
)
g
(
k
)
,
{\displaystyle (fg)^{(n)}=\sum \limits _{k=0}^{n}{C_{n}^{k}f^{(n-k)}g^{(k)}},}
C
n
k
{\displaystyle C_{n}^{k}}
–Ī–ł–Ĺ–ĺ–ľ–ł–į–Ľ—Ć–Ĺ—č–Ķ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č .–°–Ľ–Ķ–ī—É—é—Č–ł–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ —Ā–Ľ—É–∂–į—ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ–ľ –ļ –Ņ—Ä–į–≤–ł–Ľ–į–ľ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä–ĺ–≤–į–Ĺ–ł—Ź:
–Ķ—Ā–Ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ä—É–Ķ–ľ–į –Ĺ–į –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–Ķ
(
a
,
b
)
{\displaystyle (a,b)}
(
a
,
b
)
{\displaystyle (a,b)}
y
(
x
)
=
|
x
|
{\displaystyle y(x)=|x|}
[
− ‚ąí -->
1
,
1
]
{\displaystyle [-1,1]}
–Ķ—Ā–Ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź –ł–ľ–Ķ–Ķ—ā –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ļ –ľ–į–ļ—Ā–ł–ľ—É–ľ/–ľ–ł–Ĺ–ł–ľ—É–ľ –Ņ—Ä–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł–ł –į—Ä–≥—É–ľ–Ķ–Ĺ—ā–į, —Ä–į–≤–Ĺ–ĺ–ľ
x
{\displaystyle x}
f
′
(
x
)
=
0
{\displaystyle f'(x)=0}
–Ľ–Ķ–ľ–ľ–į –§–Ķ—Ä–ľ–į );
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –ī–į–Ĺ–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–į, –Ĺ–ĺ —É —Ä–į–∑–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—č–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ.
(
f
(
x
)
g
(
x
)
)
′
=
f
(
x
)
g
(
x
)
(
g
′
(
x
)
ln
‚Ā° -->
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
)
(
∀ ‚ąÄ -->
x
∈ ‚ąą -->
D
f
:
f
(
x
)
>
0
)
{\displaystyle (f(x)^{g(x)})'=f(x)^{g(x)}\left(g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}}\right)(\forall x\in D_{f}:f(x)>0)}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
y
=
f
(
x
)
g
(
x
)
{\displaystyle y=f(x)^{g(x)}}
ln
‚Ā° -->
y
=
g
(
x
)
ln
‚Ā° -->
f
(
x
)
{\displaystyle \ln y=g(x)\ln f(x)}
y
′
y
=
g
′
(
x
)
ln
‚Ā° -->
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
{\displaystyle {\frac {y'}{y}}=g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}}}
y
′
=
y
(
g
′
(
x
)
ln
‚Ā° -->
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
)
{\displaystyle y'=y\left(g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}}\right)}
y
′
=
f
(
x
)
g
(
x
)
(
g
′
(
x
)
ln
‚Ā° -->
f
(
x
)
+
g
(
x
)
f
′
(
x
)
f
(
x
)
)
{\displaystyle y'=f(x)^{g(x)}(g'(x)\ln f(x)+{\frac {g(x)f'(x)}{f(x)}})}
‚Ė†
–§—É–Ĺ–ļ—Ü–ł—Ź
f
(
x
)
{\displaystyle f(x)}
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź
f
′
(
x
)
{\displaystyle f'(x)}
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł–Ķ
x
α őĪ -->
{\displaystyle x^{\alpha }}
α őĪ -->
⋅ ‚čÖ -->
x
α őĪ -->
− ‚ąí -->
1
{\displaystyle \alpha \cdot x^{\alpha -1}}
a
x
{\displaystyle a^{x}}
a
x
⋅ ‚čÖ -->
ln
‚Ā° -->
a
{\displaystyle a^{x}\cdot \ln {a}}
log
a
‚Ā° -->
x
{\displaystyle \log _{a}{x}}
1
x
⋅ ‚čÖ -->
ln
‚Ā° -->
a
{\displaystyle {\frac {1}{x\cdot \ln {a}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
log
a
‚Ā° -->
x
)
′
=
1
ln
‚Ā° -->
a
⋅ ‚čÖ -->
(
ln
‚Ā° -->
x
)
′
{\displaystyle (\log _{a}x)'={\frac {1}{\ln {a}}}\cdot (\ln {x})'}
–£–∑–Ĺ–į–Ķ–ľ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é
ln
‚Ā° -->
x
{\displaystyle \ln {x}}
–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł :
y
x
=
ln
‚Ā° -->
x
⇒ ‚áí -->
x
y
=
e
y
,
{\displaystyle y_{x}=\ln {x}\Rightarrow x_{y}=e^{y},}
y
x
′
=
(
ln
‚Ā° -->
x
)
′
=
1
(
e
y
)
′
=
1
e
y
=
1
x
{\displaystyle y_{x}'=(\ln {x})'={\frac {1}{(e^{y})'}}={\frac {1}{e^{y}}}={\frac {1}{x}}}
–ü–ĺ–Ľ—É—á–į–Ķ–ľ:
(
log
a
‚Ā° -->
x
)
′
=
1
x
⋅ ‚čÖ -->
ln
‚Ā° -->
a
{\displaystyle (\log _{a}{x})'={\frac {1}{x\cdot \ln {a}}}}
sin
‚Ā° -->
x
{\displaystyle \sin x}
cos
‚Ā° -->
x
{\displaystyle \cos x}
cos
‚Ā° -->
x
{\displaystyle \cos x}
− ‚ąí -->
sin
‚Ā° -->
x
{\displaystyle -\sin x}
t
g
x
{\displaystyle \mathrm {tg} \ x}
1
cos
2
‚Ā° -->
x
{\displaystyle {\frac {1}{\cos ^{2}{x}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ 2
(
t
g
x
)
′
=
(
s
i
n
(
x
)
c
o
s
(
x
)
)
′
=
(
s
i
n
(
x
)
)
′
⋅ ‚čÖ -->
c
o
s
(
x
)
− ‚ąí -->
s
i
n
(
x
)
⋅ ‚čÖ -->
(
c
o
s
(
x
)
)
′
c
o
s
2
(
x
)
=
c
o
s
(
x
)
⋅ ‚čÖ -->
c
o
s
(
x
)
− ‚ąí -->
s
i
n
(
x
)
⋅ ‚čÖ -->
(
− ‚ąí -->
s
i
n
(
x
)
)
c
o
s
2
(
x
)
=
c
o
s
2
(
x
)
+
s
i
n
2
(
x
)
c
o
s
2
(
x
)
=
1
c
o
s
2
(
x
)
{\displaystyle (tgx)'=({\frac {sin(x)}{cos(x)}})'={\frac {(sin(x))'\cdot cos(x)-sin(x)\cdot (cos(x))'}{cos^{2}(x)}}={\frac {cos(x)\cdot cos(x)-sin(x)\cdot (-sin(x))}{cos^{2}(x)}}={\frac {cos^{2}(x)+sin^{2}(x)}{cos^{2}(x)}}={\frac {1}{cos^{2}(x)}}}
c
t
g
x
{\displaystyle \mathrm {ctg} \ x}
− ‚ąí -->
1
sin
2
‚Ā° -->
x
{\displaystyle -{\frac {1}{\sin ^{2}{x}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
c
t
g
x
)
′
=
(
c
o
s
(
x
)
s
i
n
(
x
)
)
′
=
(
c
o
s
(
x
)
)
′
⋅ ‚čÖ -->
s
i
n
(
x
)
− ‚ąí -->
c
o
s
(
x
)
⋅ ‚čÖ -->
(
s
i
n
(
x
)
)
′
s
i
n
2
(
x
)
=
− ‚ąí -->
s
i
n
(
x
)
⋅ ‚čÖ -->
s
i
n
(
x
)
+
c
o
s
(
x
)
⋅ ‚čÖ -->
c
o
s
(
x
)
s
i
n
2
(
x
)
=
− ‚ąí -->
s
i
n
2
(
x
)
+
c
o
s
2
(
x
)
s
i
n
2
(
x
)
=
− ‚ąí -->
1
s
i
n
2
(
x
)
{\displaystyle (ctgx)'=({\frac {cos(x)}{sin(x)}})'={\frac {(cos(x))'\cdot sin(x)-cos(x)\cdot (sin(x))'}{sin^{2}(x)}}={\frac {-sin(x)\cdot sin(x)+cos(x)\cdot cos(x)}{sin^{2}(x)}}=-{\frac {sin^{2}(x)+cos^{2}(x)}{sin^{2}(x)}}=-{\frac {1}{sin^{2}(x)}}}
s
e
c
x
{\displaystyle \mathrm {sec} \ x}
s
e
c
x
⋅ ‚čÖ -->
t
g
x
{\displaystyle \mathrm {sec} \ x\cdot \mathrm {tg} \ x}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
s
e
c
(
x
)
)
′
=
(
1
c
o
s
(
x
)
)
′
=
(
1
)
′
⋅ ‚čÖ -->
c
o
s
(
x
)
− ‚ąí -->
1
⋅ ‚čÖ -->
(
c
o
s
(
x
)
)
′
c
o
s
2
(
x
)
=
s
i
n
(
x
)
c
o
s
2
(
x
)
=
s
e
c
(
x
)
⋅ ‚čÖ -->
t
g
(
x
)
{\displaystyle (sec(x))'=({\frac {1}{cos(x)}})'={\frac {(1)'\cdot cos(x)-1\cdot (cos(x))'}{cos^{2}(x)}}={\frac {sin(x)}{cos^{2}(x)}}=sec(x)\cdot tg(x)}
c
o
s
e
c
x
{\displaystyle \mathrm {cosec} \ x}
− ‚ąí -->
c
o
s
e
c
x
⋅ ‚čÖ -->
c
t
g
x
{\displaystyle -\mathrm {cosec} \ x\cdot \mathrm {ctg} \ x}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
c
o
s
e
c
(
x
)
)
′
=
(
1
s
i
n
(
x
)
)
′
=
(
1
)
′
⋅ ‚čÖ -->
s
i
n
(
x
)
− ‚ąí -->
1
⋅ ‚čÖ -->
(
s
i
n
(
x
)
)
′
s
i
n
2
(
x
)
=
− ‚ąí -->
c
o
s
(
x
)
s
i
n
2
(
x
)
=
− ‚ąí -->
c
o
s
e
s
(
x
)
⋅ ‚čÖ -->
c
t
g
(
x
)
{\displaystyle (cosec(x))'=({\frac {1}{sin(x)}})'={\frac {(1)'\cdot sin(x)-1\cdot (sin(x))'}{sin^{2}(x)}}=-{\frac {cos(x)}{sin^{2}(x)}}=-coses(x)\cdot ctg(x)}
arcsin
‚Ā° -->
x
{\displaystyle \arcsin {x}}
1
1
− ‚ąí -->
x
2
{\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
arccos
‚Ā° -->
x
{\displaystyle \arccos {x}}
− ‚ąí -->
1
1
− ‚ąí -->
x
2
{\displaystyle -{\frac {1}{\sqrt {1-x^{2}}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
a
r
c
t
g
x
{\displaystyle \mathrm {arctg} \ x}
1
1
+
x
2
{\displaystyle {\frac {1}{1+x^{2}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
a
r
c
c
t
g
x
{\displaystyle \mathrm {arcctg} \ x}
− ‚ąí -->
1
1
+
x
2
{\displaystyle -{\frac {1}{1+x^{2}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
a
r
c
s
e
c
x
{\displaystyle \mathrm {arcsec} \ x}
1
|
x
|
x
2
− ‚ąí -->
1
{\displaystyle {\frac {1}{|x|{\sqrt {x^{2}-1}}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
–Ě–į–Ļ—ā–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –į—Ä–ļ—Ā–Ķ–ļ–į–Ĺ—Ā–į –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł –Ņ–ĺ–ľ–ĺ—Č–ł —ā–ĺ–∂–ī–Ķ—Ā—ā–≤–į:
a
r
c
s
e
c
(
x
)
=
a
r
c
c
o
s
(
1
x
)
{\displaystyle arcsec(x)=arccos({\frac {1}{x}})}
–Ę–Ķ–Ņ–Ķ—Ä—Ć –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –ĺ–Ī–Ķ–ł—Ö —á–į—Ā—ā–Ķ–Ļ —ć—ā–ĺ–≥–ĺ —ā–ĺ–∂–ī–Ķ—Ā—ā–≤–į.
(
a
r
c
s
e
c
(
x
)
)
′
=
(
a
r
c
c
o
s
(
1
x
)
)
′
{\displaystyle (arcsec(x))'=(arccos({\frac {1}{x}}))'}
(
a
r
c
s
e
c
(
x
)
)
′
=
− ‚ąí -->
1
1
− ‚ąí -->
1
x
2
⋅ ‚čÖ -->
(
− ‚ąí -->
1
x
2
)
{\displaystyle (arcsec(x))'=-{\frac {1}{\sqrt {1-{\frac {1}{x^{2}}}}}}\cdot (-{\frac {1}{x^{2}}})}
(
a
r
c
s
e
c
(
x
)
)
′
=
1
x
2
x
2
− ‚ąí -->
1
x
2
{\displaystyle (arcsec(x))'={\frac {1}{x^{2}{\sqrt {\frac {x^{2}-1}{x^{2}}}}}}}
(
a
r
c
s
e
c
(
x
)
)
′
=
1
x
2
x
2
− ‚ąí -->
1
|
x
|
{\displaystyle (arcsec(x))'={\frac {1}{x^{2}{\frac {\sqrt {x^{2}-1}}{|x|}}}}}
–ü–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź.
(
a
r
c
s
e
c
(
x
)
)
′
=
1
|
x
|
x
2
− ‚ąí -->
1
{\displaystyle (arcsec(x))'={\frac {1}{|x|{\sqrt {x^{2}-1}}}}}
a
r
c
c
o
s
e
c
x
{\displaystyle \mathrm {arccosec} \ x}
− ‚ąí -->
1
|
x
|
x
2
− ‚ąí -->
1
{\displaystyle -{\frac {1}{|x|{\sqrt {x^{2}-1}}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
s
h
x
{\displaystyle \mathrm {sh} \ x}
c
h
x
{\displaystyle \mathrm {ch} \ x}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
sh
‚Ā° -->
x
)
′
=
(
e
x
− ‚ąí -->
e
− ‚ąí -->
x
2
)
′
=
1
2
⋅ ‚čÖ -->
(
e
x
− ‚ąí -->
e
− ‚ąí -->
x
)
′
=
1
2
⋅ ‚čÖ -->
(
e
x
− ‚ąí -->
(
− ‚ąí -->
1
)
⋅ ‚čÖ -->
e
− ‚ąí -->
x
)
=
e
x
+
e
− ‚ąí -->
x
2
=
ch
‚Ā° -->
x
{\displaystyle (\operatorname {sh} {x})'=\left({\frac {e^{x}-e^{-x}}{2}}\right)'={\frac {1}{2}}\cdot (e^{x}-e^{-x})'={\frac {1}{2}}\cdot (e^{x}-(-1)\cdot e^{-x})={\frac {e^{x}+e^{-x}}{2}}=\operatorname {ch} {x}}
c
h
x
{\displaystyle \mathrm {ch} \ x}
s
h
x
{\displaystyle \mathrm {sh} \ x}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
ch
‚Ā° -->
x
)
′
=
(
e
x
+
e
− ‚ąí -->
x
2
)
′
=
1
2
⋅ ‚čÖ -->
(
e
x
+
e
− ‚ąí -->
x
)
′
=
1
2
⋅ ‚čÖ -->
(
e
x
+
(
− ‚ąí -->
1
)
⋅ ‚čÖ -->
e
− ‚ąí -->
x
)
=
(
e
x
− ‚ąí -->
e
− ‚ąí -->
x
2
)
=
sh
‚Ā° -->
x
{\displaystyle (\operatorname {ch} {x})'=\left({\frac {e^{x}+e^{-x}}{2}}\right)'={\frac {1}{2}}\cdot (e^{x}+e^{-x})'={\frac {1}{2}}\cdot (e^{x}+(-1)\cdot e^{-x})=\left({\frac {e^{x}-e^{-x}}{2}}\right)=\operatorname {sh} {x}}
t
h
x
{\displaystyle \mathrm {th} \ x}
1
c
h
2
x
{\displaystyle {\frac {1}{\mathrm {ch} ^{2}\ x}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
t
h
(
x
)
)
′
=
(
s
h
(
x
)
c
h
(
x
)
)
′
=
(
s
h
(
x
)
)
′
⋅ ‚čÖ -->
c
h
(
x
)
− ‚ąí -->
s
h
(
x
)
⋅ ‚čÖ -->
(
c
h
(
x
)
)
′
c
h
2
(
x
)
=
c
h
(
x
)
⋅ ‚čÖ -->
c
h
(
x
)
− ‚ąí -->
s
h
(
x
)
⋅ ‚čÖ -->
s
h
(
x
)
c
h
2
(
x
)
=
c
h
2
(
x
)
− ‚ąí -->
s
h
2
(
x
)
c
h
2
(
x
)
=
1
c
h
2
(
x
)
{\displaystyle (th(x))'=({\frac {sh(x)}{ch(x)}})'={\frac {(sh(x))'\cdot ch(x)-sh(x)\cdot (ch(x))'}{ch^{2}(x)}}={\frac {ch(x)\cdot ch(x)-sh(x)\cdot sh(x)}{ch^{2}(x)}}={\frac {ch^{2}(x)-sh^{2}(x)}{ch^{2}(x)}}={\frac {1}{ch^{2}(x)}}}
c
t
h
x
{\displaystyle \mathrm {cth} \ x}
− ‚ąí -->
1
s
h
2
x
{\displaystyle -{\frac {1}{\mathrm {sh} ^{2}\ x}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
c
t
h
x
)
′
=
(
c
h
(
x
)
s
h
(
x
)
)
′
=
(
c
h
(
x
)
)
′
⋅ ‚čÖ -->
s
h
(
x
)
− ‚ąí -->
c
h
(
x
)
⋅ ‚čÖ -->
(
s
h
(
x
)
)
′
s
h
2
(
x
)
=
s
h
(
x
)
⋅ ‚čÖ -->
s
h
(
x
)
− ‚ąí -->
c
h
(
x
)
⋅ ‚čÖ -->
c
h
(
x
)
s
h
2
(
x
)
=
s
h
2
(
x
)
− ‚ąí -->
c
h
2
(
x
)
s
h
2
(
x
)
=
− ‚ąí -->
1
s
h
2
(
x
)
{\displaystyle (cthx)'=({\frac {ch(x)}{sh(x)}})'={\frac {(ch(x))'\cdot sh(x)-ch(x)\cdot (sh(x))'}{sh^{2}(x)}}={\frac {sh(x)\cdot sh(x)-ch(x)\cdot ch(x)}{sh^{2}(x)}}={\frac {sh^{2}(x)-ch^{2}(x)}{sh^{2}(x)}}=-{\frac {1}{sh^{2}(x)}}}
s
c
h
x
{\displaystyle \mathrm {sch} \ x}
− ‚ąí -->
sh
‚Ā° -->
(
x
)
ch
2
‚Ā° -->
(
x
)
{\displaystyle -{\frac {\operatorname {sh} (x)}{\operatorname {ch} ^{2}(x)}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
s
c
h
(
x
)
)
′
=
(
1
c
h
(
x
)
)
′
=
(
1
)
′
⋅ ‚čÖ -->
c
h
(
x
)
− ‚ąí -->
1
⋅ ‚čÖ -->
(
c
h
(
x
)
)
′
c
h
2
(
x
)
=
− ‚ąí -->
s
h
(
x
)
c
h
2
(
x
)
{\displaystyle (sch(x))'=({\frac {1}{ch(x)}})'={\frac {(1)'\cdot ch(x)-1\cdot (ch(x))'}{ch^{2}(x)}}=-{\frac {sh(x)}{ch^{2}(x)}}}
c
s
c
h
x
{\displaystyle \mathrm {csch} \ x}
− ‚ąí -->
ch
‚Ā° -->
(
x
)
sh
2
‚Ā° -->
(
x
)
{\displaystyle -{\frac {\operatorname {ch} (x)}{\operatorname {sh} ^{2}(x)}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
c
s
c
h
(
x
)
)
′
=
(
1
s
h
(
x
)
)
′
=
(
1
)
′
⋅ ‚čÖ -->
s
h
(
x
)
− ‚ąí -->
1
⋅ ‚čÖ -->
(
s
h
(
x
)
)
′
s
h
2
(
x
)
=
− ‚ąí -->
c
h
(
x
)
s
h
2
(
x
)
{\displaystyle (csch(x))'=({\frac {1}{sh(x)}})'={\frac {(1)'\cdot sh(x)-1\cdot (sh(x))'}{sh^{2}(x)}}=-{\frac {ch(x)}{sh^{2}(x)}}}
a
r
s
h
x
{\displaystyle \mathrm {arsh} \ x}
1
x
2
+
1
{\displaystyle {\frac {1}{\sqrt {x^{2}+1}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
a
r
s
h
(
x
)
)
′
=
(
ln
‚Ā° -->
(
x
+
x
2
+
1
)
)
′
=
1
x
+
x
2
+
1
⋅ ‚čÖ -->
(
x
+
x
2
+
1
)
′
=
1
x
+
x
2
+
1
⋅ ‚čÖ -->
(
(
x
)
′
+
(
x
2
+
1
)
′
)
=
1
x
+
x
2
+
1
⋅ ‚čÖ -->
(
1
+
(
x
2
+
1
)
′
)
=
1
x
+
x
2
+
1
⋅ ‚čÖ -->
(
1
+
1
2
x
2
+
1
⋅ ‚čÖ -->
(
x
2
+
1
)
′
)
=
1
x
+
x
2
+
1
⋅ ‚čÖ -->
(
1
+
2
x
2
x
2
+
1
)
=
1
x
+
x
2
+
1
⋅ ‚čÖ -->
(
x
+
x
2
+
1
x
2
+
1
)
=
x
+
x
2
+
1
(
x
+
x
2
+
1
)
⋅ ‚čÖ -->
(
x
2
+
1
)
=
1
x
2
+
1
{\displaystyle (arsh(x))'=(\ln {(x+{\sqrt {x^{2}+1}})})'={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (x+{\sqrt {x^{2}+1}})'={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot ((x)'+({\sqrt {x^{2}+1}})')={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (1+({\sqrt {x^{2}+1}})')={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (1+{\frac {1}{2{\sqrt {x^{2}+1}}}}\cdot (x^{2}+1)')={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot (1+{\frac {2x}{2{\sqrt {x^{2}+1}}}})={\frac {1}{x+{\sqrt {x^{2}+1}}}}\cdot ({\frac {x+{\sqrt {x^{2}+1}}}{\sqrt {x^{2}+1}}})={\frac {x+{\sqrt {x^{2}+1}}}{(x+{\sqrt {x^{2}+1}})\cdot ({\sqrt {x^{2}+1}})}}={\frac {1}{\sqrt {x^{2}+1}}}}
a
r
c
h
x
{\displaystyle \mathrm {arch} \ x}
1
x
2
− ‚ąí -->
1
{\displaystyle {\frac {1}{\sqrt {x^{2}-1}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
a
r
c
h
(
x
)
)
′
=
(
ln
‚Ā° -->
(
x
+
x
2
− ‚ąí -->
1
)
)
′
=
1
x
+
x
2
− ‚ąí -->
1
⋅ ‚čÖ -->
(
x
+
x
2
− ‚ąí -->
1
)
′
=
1
x
+
x
2
− ‚ąí -->
1
⋅ ‚čÖ -->
(
(
x
)
′
+
(
x
2
− ‚ąí -->
1
)
′
)
=
1
x
+
x
2
− ‚ąí -->
1
⋅ ‚čÖ -->
(
1
+
(
x
2
− ‚ąí -->
1
)
′
)
=
1
x
+
x
2
− ‚ąí -->
1
⋅ ‚čÖ -->
(
1
+
1
2
x
2
− ‚ąí -->
1
⋅ ‚čÖ -->
(
x
2
− ‚ąí -->
1
)
′
)
=
1
x
+
x
2
− ‚ąí -->
1
⋅ ‚čÖ -->
(
1
+
2
x
2
x
2
− ‚ąí -->
1
)
=
1
x
+
x
2
− ‚ąí -->
1
⋅ ‚čÖ -->
(
x
+
x
2
− ‚ąí -->
1
x
2
− ‚ąí -->
1
)
=
x
+
x
2
− ‚ąí -->
1
(
x
+
x
2
− ‚ąí -->
1
)
⋅ ‚čÖ -->
(
x
2
− ‚ąí -->
1
)
=
1
x
2
− ‚ąí -->
1
{\displaystyle (arch(x))'=(\ln {(x+{\sqrt {x^{2}-1}})})'={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (x+{\sqrt {x^{2}-1}})'={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot ((x)'+({\sqrt {x^{2}-1}})')={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (1+({\sqrt {x^{2}-1}})')={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (1+{\frac {1}{2{\sqrt {x^{2}-1}}}}\cdot (x^{2}-1)')={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot (1+{\frac {2x}{2{\sqrt {x^{2}-1}}}})={\frac {1}{x+{\sqrt {x^{2}-1}}}}\cdot ({\frac {x+{\sqrt {x^{2}-1}}}{\sqrt {x^{2}-1}}})={\frac {x+{\sqrt {x^{2}-1}}}{(x+{\sqrt {x^{2}-1}})\cdot ({\sqrt {x^{2}-1}})}}={\frac {1}{\sqrt {x^{2}-1}}}}
a
r
t
h
x
{\displaystyle \mathrm {arth} \ x}
1
1
− ‚ąí -->
x
2
{\displaystyle {\frac {1}{1-x^{2}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
a
r
t
h
x
)
′
=
(
1
2
⋅ ‚čÖ -->
ln
‚Ā° -->
(
1
+
x
1
− ‚ąí -->
x
)
)
′
=
1
2
⋅ ‚čÖ -->
1
− ‚ąí -->
x
1
+
x
⋅ ‚čÖ -->
(
1
+
x
1
− ‚ąí -->
x
)
′
=
1
2
⋅ ‚čÖ -->
1
− ‚ąí -->
x
1
+
x
⋅ ‚čÖ -->
(
1
+
x
)
′
(
1
− ‚ąí -->
x
)
− ‚ąí -->
(
1
+
x
)
(
1
− ‚ąí -->
x
)
′
(
1
− ‚ąí -->
x
)
2
=
1
2
⋅ ‚čÖ -->
1
− ‚ąí -->
x
1
+
x
⋅ ‚čÖ -->
2
(
1
− ‚ąí -->
x
)
2
=
1
1
− ‚ąí -->
x
2
{\displaystyle ({\displaystyle \mathrm {arth} \ x})'={\biggl (}{\frac {1}{2}}\cdot \ln {\biggl (}{\frac {1+x}{1-x}}{\biggl )}{\biggl )}'={\frac {1}{2}}\cdot {\frac {1-x}{1+x}}\cdot {\biggl (}{\frac {1+x}{1-x}}{\biggl )}'={\frac {1}{2}}\cdot {\frac {1-x}{1+x}}\cdot {\frac {(1+x)'(1-x)-(1+x)(1-x)'}{(1-x)^{2}}}={\frac {1}{2}}\cdot {\frac {1-x}{1+x}}\cdot {\frac {2}{(1-x)^{2}}}={\frac {1}{1-x^{2}}}}
a
r
c
t
h
x
{\displaystyle \mathrm {arcth} \ x}
1
1
− ‚ąí -->
x
2
{\displaystyle {\frac {1}{1-x^{2}}}}
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ
(
a
r
c
t
h
x
)
′
=
(
1
2
⋅ ‚čÖ -->
ln
‚Ā° -->
(
x
+
1
x
− ‚ąí -->
1
)
)
′
=
1
2
⋅ ‚čÖ -->
x
− ‚ąí -->
1
x
+
1
⋅ ‚čÖ -->
(
x
+
1
x
− ‚ąí -->
1
)
′
=
1
2
⋅ ‚čÖ -->
x
− ‚ąí -->
1
x
+
1
⋅ ‚čÖ -->
(
x
+
1
)
′
(
x
− ‚ąí -->
1
)
− ‚ąí -->
(
x
+
1
)
(
x
− ‚ąí -->
1
)
′
(
x
− ‚ąí -->
1
)
2
=
1
2
⋅ ‚čÖ -->
x
− ‚ąí -->
1
x
+
1
⋅ ‚čÖ -->
− ‚ąí -->
2
(
x
− ‚ąí -->
1
)
2
=
1
1
− ‚ąí -->
x
2
{\displaystyle ({\displaystyle \mathrm {arcth} \ x})'={\biggl (}{\frac {1}{2}}\cdot \ln {\biggl (}{\frac {x+1}{x-1}}{\biggl )}{\biggl )}'={\frac {1}{2}}\cdot {\frac {x-1}{x+1}}\cdot {\biggl (}{\frac {x+1}{x-1}}{\biggl )}'={\frac {1}{2}}\cdot {\frac {x-1}{x+1}}\cdot {\frac {(x+1)'(x-1)-(x+1)(x-1)'}{(x-1)^{2}}}={\frac {1}{2}}\cdot {\frac {x-1}{x+1}}\cdot {\frac {-2}{(x-1)^{2}}}={\frac {1}{1-x^{2}}}}
a
r
s
e
c
h
x
{\displaystyle \mathrm {arsech} \ x}
− ‚ąí -->
1
x
(
x
+
1
)
1
− ‚ąí -->
x
1
+
x
{\displaystyle -{\frac {1}{x(x+1){\sqrt {\frac {1-x}{1+x}}}}}}
a
r
c
s
c
h
x
{\displaystyle \mathrm {arcsch} \ x}
− ‚ąí -->
1
x
(
x
+
1
)
1
+
1
x
2
{\displaystyle -{\frac {1}{x(x+1){\sqrt {1+{\frac {1}{x^{2}}}}}}}}
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–ľ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—É—é –≤–Ķ–ļ—ā–ĺ—Ä-—Ą—É–Ĺ–ļ—Ü–ł–ł
r
(
t
)
{\displaystyle \mathbf {r} (t)}
d
d
t
r
(
t
)
=
lim
h
→ ‚Üí -->
0
r
(
t
+
h
)
− ‚ąí -->
r
(
t
)
h
{\displaystyle {\frac {d}{dt}}\mathbf {r} (t)=\lim _{h\to 0}{\frac {\mathbf {r} (t+h)-\mathbf {r} (t)}{h}}}
–ē—Ā–Ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –≤ —ā–ĺ—á–ļ–Ķ
t
{\displaystyle t}
x
′
(
t
)
,
y
′
(
t
)
,
z
′
(
t
)
{\displaystyle x'(t),\ y'(t),\ z'(t)}
–°–≤–ĺ–Ļ—Ā—ā–≤–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ –≤–Ķ–ļ—ā–ĺ—Ä-—Ą—É–Ĺ–ļ—Ü–ł–ł (–≤—Ā—é–ī—É –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į–Ķ—ā—Ā—Ź, —á—ā–ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č–Ķ —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā):
d
d
t
(
r
1
(
t
)
+
r
2
(
t
)
)
=
d
r
1
(
t
)
d
t
+
d
r
2
(
t
)
d
t
{\displaystyle {\frac {d}{dt}}(\mathbf {r_{1}} (t)+\mathbf {r_{2}} (t))={\frac {d\mathbf {r_{1}} (t)}{dt}}+{\frac {d\mathbf {r_{2}} (t)}{dt}}}
d
d
t
(
f
(
t
)
r
(
t
)
)
=
d
f
(
t
)
d
t
r
(
t
)
+
f
(
t
)
d
r
(
t
)
d
t
{\displaystyle {\frac {d}{dt}}(f(t)\mathbf {r} (t))={\frac {df(t)}{dt}}\mathbf {r} (t)+f(t){\frac {d\mathbf {r} (t)}{dt}}}
f
(
t
)
{\displaystyle f(t)}
—Ā–ļ–į–Ľ—Ź—Ä–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź .
d
d
t
(
r
1
(
t
)
r
2
(
t
)
)
=
d
r
1
(
t
)
d
t
r
2
(
t
)
+
r
1
(
t
)
d
r
2
(
t
)
d
t
{\displaystyle {\frac {d}{dt}}(\mathbf {r_{1}} (t)\mathbf {r_{2}} (t))={\frac {d\mathbf {r_{1}} (t)}{dt}}\mathbf {r_{2}} (t)+\mathbf {r_{1}} (t){\frac {d\mathbf {r_{2}} (t)}{dt}}}
—Ā–ļ–į–Ľ—Ź—Ä–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź .
d
d
t
[
r
1
(
t
)
,
r
2
(
t
)
]
=
[
d
r
1
(
t
)
d
t
,
r
2
(
t
)
]
+
[
r
1
(
t
)
,
d
r
2
(
t
)
d
t
]
{\displaystyle {\frac {d}{dt}}[\mathbf {r_{1}} (t),\mathbf {r_{2}} (t)]=\left[{\frac {d\mathbf {r_{1}} (t)}{dt}},\mathbf {r_{2}} (t)\right]+\left[\mathbf {r_{1}} (t),{\frac {d\mathbf {r_{2}} (t)}{dt}}\right]}
–≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź .
d
d
t
(
a
(
t
)
,
b
(
t
)
,
c
(
t
)
)
=
(
d
a
(
t
)
d
t
,
b
(
t
)
,
c
(
t
)
)
+
(
a
(
t
)
,
d
b
(
t
)
d
t
,
c
(
t
)
)
+
(
a
(
t
)
,
b
(
t
)
,
d
c
(
t
)
d
t
)
{\displaystyle {\frac {d}{dt}}(\mathbf {a} (t),\mathbf {b} (t),\mathbf {c} (t))=\left({\frac {d\mathbf {a} (t)}{dt}},\mathbf {b} (t),\mathbf {c} (t)\right)+\left(\mathbf {a} (t),{\frac {d\mathbf {b} (t)}{dt}},\mathbf {c} (t)\right)+\left(\mathbf {a} (t),\mathbf {b} (t),{\frac {d\mathbf {c} (t)}{dt}}\right)}
—Ā–ľ–Ķ—ą–į–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź .
–ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –Ē–∂–Ķ–ļ—Ā–ĺ–Ĺ–į[ 5]
D
x
q
f
(
x
)
=
f
(
q
x
)
− ‚ąí -->
f
(
x
)
(
q
− ‚ąí -->
1
)
x
.
{\displaystyle D_{x}^{q}f(x)={\frac {f(qx)-f(x)}{(q-1)x}}.}
‚ÜĎ –ö–ĺ–Ľ–ľ–ĺ–≥–ĺ—Ä–ĺ–≤ –ź. –Ě. , –ź–Ī—Ä–į–ľ–ĺ–≤ –ź. –ú. , –Ē—É–ī–Ĺ–ł—Ü—č–Ĺ –ģ. –ü.ISBN 5-09-006088-6 . ‚ÄĒ C. 155‚ÄĒ156‚ÜĎ –ö–ĺ–ľ–ļ–ĺ–≤ –ď. –Ē. , –õ–Ķ–≤—ą–ł–Ĺ –Ď. –í., –°–Ķ–ľ–Ķ–Ĺ–ĺ–≤ –õ. –ö.–ú. : –Ě–į—É–ļ–į , 1977. ‚ÄĒ –Ę. 1. 1724‚ÄĒ1917. ‚ÄĒ –°. 173.‚ÜĎ –ü—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź —Ā—É–ľ–ľ—č —Ä–į–≤–Ĺ–į —Ā—É–ľ–ľ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö
‚ÜĎ –ě—ā—Ā—é–ī–į, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź —Ą—É–Ĺ–ļ—Ü–ł–ł –ł –ļ–ĺ–Ĺ—Ā—ā–į–Ĺ—ā—č —Ä–į–≤–Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—é –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–ĺ–Ļ —ć—ā–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ĺ–į –ļ–ĺ–Ĺ—Ā—ā–į–Ĺ—ā—É
‚ÜĎ A.I. Olemskoi, S.S. Borysov,a, and I.A. Shuda. Statistical field theories deformed within different calculi (–Ĺ–Ķ–ĺ–Ņ—Ä.) . –Ē–į—ā–į –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź: 21 –į–Ņ—Ä–Ķ–Ľ—Ź 2014. –ź—Ä—Ö–ł–≤–ł—Ä–ĺ–≤–į–Ĺ–ĺ 21 —Ā–Ķ–Ĺ—ā—Ź–Ī—Ä—Ź 2017 –≥–ĺ–ī–į.
–í–ł–Ľ–Ķ–Ĺ–ļ–ł–Ĺ –Ě., –ú–ĺ—Ä–ī–ļ–ĺ–≤–ł—á –ź. –ß—ā–ĺ —ā–į–ļ–ĺ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ–į—Ź // –ö–≤–į–Ĺ—ā. ‚ÄĒ 1975. ‚ÄĒ ‚ĄĖ 12 .–í. –ď. –Ď–ĺ–Ľ—ā—Ź–Ĺ—Ā–ļ–ł–Ļ ,–ü–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ—č–Ķ –Ľ–Ķ–ļ—Ü–ł–ł –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ ¬Ľ, –í—č–Ņ—É—Ā–ļ 17, –ď–ĺ—Ā—ā–Ķ—Ö–ł–∑–ī–į—ā 1955 –≥., 64 —Ā—ā—Ä.–í. –ź. –ď—É—Ā–Ķ–≤ , –ź. –ď. –ú–ĺ—Ä–ī–ļ–ĺ–≤–ł—á ¬ę–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į¬Ľ–ď. –ú. –§–ł—Ö—ā–Ķ–Ĺ–≥–ĺ–Ľ—Ć—Ü ¬ę–ö—É—Ä—Ā –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ł –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ł—Ā—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź ¬Ľ, —ā–ĺ–ľ 1–í. –ú. –Ď–ĺ—Ä–ĺ–ī–ł—Ö–ł–Ĺ , –í—č—Ā—ą–į—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į , —É—á–Ķ–Ī. –Ņ–ĺ—Ā–ĺ–Ī–ł–Ķ, ISBN 5-7782-0422-1
–°—Ā—č–Ľ–ļ–ł –Ĺ–į –≤–Ĺ–Ķ—ą–Ĺ–ł–Ķ —Ä–Ķ—Ā—É—Ä—Ā—č
–Ę–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–į–Ļ—ā—č
–°–Ľ–ĺ–≤–į—Ä–ł –ł —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł–ł –í –Ī–ł–Ī–Ľ–ł–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–į—ā–į–Ľ–ĺ–≥–į—Ö


































































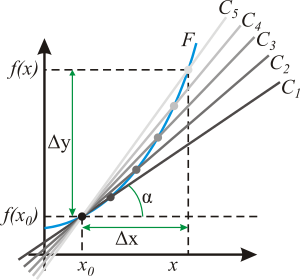






















































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)














































![{\displaystyle \left\{{\begin{matrix}x=x(t),\\y=y(t),\end{matrix}}\;\;t\in \left[T_{1};T_{2}\right]\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66c1512a040f80645b424f10cb2fc237be942c83)





![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)























































![{\displaystyle [sin(arcsin((x))]'=x'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be684108880964393fc7a90ba55f07de0e6d659a)




![{\displaystyle E(arcsin(x))=[-{\frac {\pi }{2}};{\frac {\pi }{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf2d89981edb4f950c9191723d160fe613831f5d)





![{\displaystyle [arcsin(x)+arccos(x)]'=({\frac {\pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3606594a168f2f06eb6faddfaac18f1c85324466)






![{\displaystyle [tg(arctg(x))]'=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ce9406b214a5266d0bf8282fd6aae4b59602c66)








![{\displaystyle [arctg(x)+arcctg(x)]'=({\frac {\pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f84cee67adf89ef76bfaa5c415907cce038d455)














![{\displaystyle [arccosec(x)+arcsec(x)]'=({\frac {\pi }{2}})'}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4847d93af2226f3ab5e1ba20940ec8530526b49e)









































![{\displaystyle {\frac {d}{dt}}[\mathbf {r_{1}} (t),\mathbf {r_{2}} (t)]=\left[{\frac {d\mathbf {r_{1}} (t)}{dt}},\mathbf {r_{2}} (t)\right]+\left[\mathbf {r_{1}} (t),{\frac {d\mathbf {r_{2}} (t)}{dt}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b172aa52700f4bc10de3dc186111a82e2465a50)


