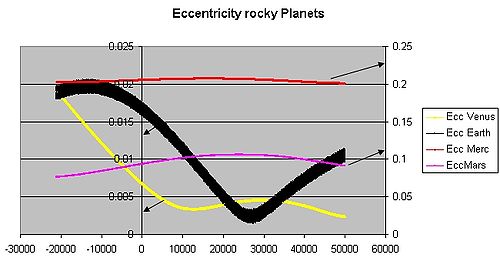
Excentricidade orbital
|
Read other articles:

Аеропорт Тролльгеттан-Венерсборг ІАТА: THN • ICAO: ESGTЗагальні дані 58°19′27″ пн. ш. 012°20′11″ сх. д. / 58.32417° пн. ш. 12.33639° сх. д. / 58.32417; 12.33639Координати: 58°19′27″ пн. ш. 012°20′11″ сх. д. / 58.32417° пн. ш. 12.33639° сх. д. / 58....

KlisoeraКлисура Dorp in Bulgarije Situering Oblast Sofia Gemeente Samokov Coördinaten 42° 20′ NB, 23° 22′ OL Algemeen Oppervlakte 30,91 km² Inwoners (31 december 2019) 199 Hoogte 1100 m Overig Postcode 2026 Netnummer 07124 Kenteken СО Portaal Bulgarije Klisoera (Bulgaars: Клисура) is een dorp in het westen van Bulgarije. Zij is gelegen in de gemeente Samokov in de oblast Sofia. Het dorp ligt 15 km van Samokov, 25 km van Doepnitsa en 40 km ten zuide...

See also: List of Olympic medalists in freestyle wrestling and Wrestling at the Summer Olympics This is the complete list of Olympic medalists in Greco-Roman wrestling. Current program Bantamweight 58 kg: 1924–1928 56 kg: 1932–1936 57 kg: 1948–1996 58 kg: 2000 55 kg: 2004–2012 59 kg: 2016 60 kg: 2020–present Games Gold Silver Bronze 1924 Parisdetails Eduard Pütsep Estonia Anselm Ahlfors Finland Väinö Ikonen Finland 1928 Amsterdamdetails Kurt Leucht Germany Jin...

此條目介紹的是小說。关于電影版本,请见「如果杜拉 (電影)」。 如果,高校棒球女子經理讀了彼得·杜拉克 もし高校野球の女子マネージャーがドラッカーの『マネジメント』を読んだら Drucker in the Dug-Out 假名 もしこうこうやきゅうのじょしマネージャーがドラッカーのマネジメントをよんだら 罗马字 Moshi Kōkō Yakyū no Joshi Manager ga Drucker no Management o Yondara 正式譯

Ngỗng Ấn ĐộTình trạng bảo tồnÍt quan tâm (IUCN 3.1)[1]Phân loại khoa họcGiới (regnum)AnimaliaNgành (phylum)ChordataLớp (class)AvesBộ (ordo)AnseriformesHọ (familia)AnatidaePhân họ (subfamilia)AnserinaeTông (tribus)AnseriniChi (genus)AnserLoài (species)A. indicusDanh pháp hai phầnAnser indicus(Latham, 1790) Danh pháp đồng nghĩa Eulabeia indica Anser indicus Ngỗng Ấn Độ hay Ngỗng đầu sọc (danh pháp hai phần: Anser indicus) ...

Cette page donne les armoiries (figures et blasonnements) des maîtres de l'ordre du Temple. Armoiries Figure Nom du maître et blasonnement Ordre du Temple d'argent à la croix pattée de gueules[1]. Ces armoiries sont ensuite attribuées à Hugues de Payns, maître de 1129 à 1136, mais il ne les a pas portées, ayant vécu avant l'apparition des premiers blasons. Robert de Craon (de 1136 à 1149) écartelé, au 1 et 4 d'argent à la croix pattée de gueules et au 2 et 3 losangé d'or et de...

Struktur Putamen dilabel pada sebelah kanan. Putamen (disingkat Pu) adalah sebuah struktur di tengah dari otak besar, di mana bersama nucleus caudatus akan membentuk striatum. Putamen merupakan bagian dari ganglia basalis yang membentuk bagian terluar dari nucleus lentiformis. Putamen dimungkinkan berperan pada integrasi sensorimotorik dan kontrol motorik. Putamen juga merupakan istilah pada ilmu botani untuk menunjukkan suatu batu di dalam buah. Pranala luar (Inggris) Diagram at uni-tuebinge...

1986年の阪神タイガース成績 セントラル・リーグ3位 60勝60敗10分 勝率.500[1]本拠地都市 兵庫県西宮市球場 阪神甲子園球場 球団組織オーナー 久万俊二郎経営母体 阪神電気鉄道監督 吉田義男選手会長 岡田彰布スローガン 3F(フレッシュ、ファイト、フォア・ザ・チーム)« 19851987 » テンプレートを表示 1986年の阪神タイガースでは、1986年の阪神タイガースに�...

Recreational diver training and certification agency PADI redirects here. For other uses, see Padi. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (July 2014) ...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Estadio Aurora – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when to remove this template message) Estadio Aurora is a football stadium in San José de Colinas, Honduras. It is currently used mostly for football matches and is the home stadium of ...

Founder of the Zion Christian Church (1885–1948) Engenas Barnabas Lekganyane (c. 1885–1948) was the founder of the Zion Christian Church (ZCC). He first formed the ZCC in 1924, and by the time of his death the church had at least 50,000 members. Under the leadership of his descendants the ZCC has gone on to have more than a million members primarily located in southern Africa.[1] It is now by far the biggest of the various Zionist Christian sects that account for roughly half ...

Hauptgebäude auf dem Campus Merseburg (sanierter Zustand 2014) Die Technische Hochschule Leuna-Merseburg (THLM), bei ihrer Gründung zunächst als Technische Hochschule für Chemie Leuna-Merseburg (THC) bezeichnet, war eine Technische Hochschule mit Promotionsrecht in Merseburg im heutigen Land Sachsen-Anhalt. Sie entstand am 1. September 1954 und wurde 1964 nach Carl Schorlemmer benannt. Auf dem Gelände der THLM wurde 1992 die als Fachhochschule konzipierte Hochschule Merseburg gegründet....

Sudan PrancisSoudan françaisKoloni di Afrika Barat Prancis1880–1960 BenderaHijau: Sudan PrancisLimau: Afrika Barat PrancisAbu-abu: Koloni Prancis lainnyaHitam: Republik PrancisHimneLa MarseillaiseIbu kotaBamako1Luas • 19591.241.238 km2 (479.245 sq mi)Populasi • 1959 4407000 SejarahEra sejarahImperialisme Baru• Didirikan k. 1880• Federasi dengan Senegal 1959 Didahului oleh Digantikan oleh Kekaisaran Wassoulou Kekaisaran Toucouleur Kerajaa...

Traditional symbol of the municipality of Cape Town The arms of Cape Town The coat of arms of Cape Town is the traditional symbol of the municipality of Cape Town. The original arms from the 20th century are no longer in official use, though no new arms have yet been adopted. History The original seal, depicting the arms of the city's founder, Jan van Riebeeck, supported by an anchor symbolising the Cape of Good Hope, was granted to the city by the Commissioner-General of the Batavian Republi...

Patung Roland sedang mengendarai kuda di Haldensleben, Sachsen-Anhalt, Jerman. Veillantif (bahasa Prancis), Vegliantin, Vegliantino atau Brigliadoro (bahasa Italia) adalah nama kuda Roland sang paladin dalam kisah-kisah chansons de geste. Nama kuda ini dalam bahasa Prancis berasal dari ungkapan yang berarti vigilant dalam bahasa Inggris atau waspada dalam bahasa Indonesia. Veillantif pertama kali disebutkan dalam puisi Chanson de Roland (v2032; laisse 151). Nama Vegliantino dalam bahasa Itali...

Hojeok redirects here. For the musical instrument, see Taepyeongso. Politics of South Korea Government Constitution of South Korea Law Human rights Legislature National Assembly Speaker Kim Jin-pyo (I) Deputy Speaker Kim Young-joo (D) Deputy Speaker Chung Jin-suk (P) Members Executive President of South Korea Yoon Suk-yeol (P) Prime Minister of South Korea Han Duck-soo (I) State Council Administrative divisions Judiciary Supreme Court of Korea Chief Justice Kim Myeong-soo Constitutional Court...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Mikologi – berita · surat kabar · buku · cendekiawan · JSTORMikologi Mikologi adalah cabang ilmu pengetahuan yang mempelajari tentang fungi (jamur) atau sering disebut juga cendawan.[1] Kajian dalam m...

Otaku no videoおたくのビデオ(Otaku no bideo)Misty May prende vita grazie all'animazione Generecommedia, parodia OAVAutoreToshio Okada, Yoshio Maruyama RegiaTakeshi Mori SceneggiaturaToshio Okada, Hiroyuki Yamaga (non accreditato) Char. designKenichi Sonoda Dir. artisticaHitoshi Nagao MusicheKōhei Tanaka StudioGainax, Studio Fantasia 1ª edizione27 settembre – 20 dicembre 1991 Episodi2 (completa) Rapporto4:3 Durata ep.50 min Edi...

Cet article est une ébauche concernant les monuments historiques français et les Côtes-d'Armor. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Palais des Congrès de Perros-GuirecPrésentationType Palais des congrèsArchitecte Christian Cacaut, André MrowiecDébut de construction 1969Propriétaire actuel CommunePatrimonialité Inscrit MH (2014)LocalisationPays FranceRégion BretagneDépartement ...

此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2015年8月19日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 爱彼迎AirbnbAirbnb驻加拿大多伦多办公室公司類型上市公司股票代號NASDAQ:ABNB成立2008年創辦人布萊恩·切斯基、喬·傑比亞、內森·布萊卡斯亞克 代表人物布萊恩·切斯基(執行長)喬·傑比亞(CPO)Nathan Blecharczyk(CTO)總部 美國�...