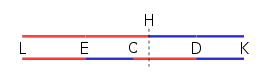
Sull'equilibrio dei piani
|
Read other articles:

Kawasan Metropolitan Kota Padang PalapaKawasan metropolitanDari atas ke bawah Kantor Gubernur Sumatera Barat, SMA Negeri 1 Padang.Negara IndonesiaProvinsi Sumatera BaratKota intiKota PadangDaerah penyangga Kota Pariaman Kabupaten Padang Pariaman Luas ŌĆó Luas daratan2.101,37 km2 (81,134 sq mi)Populasi (2022) ŌĆó Total1.451.990 Palapa (akronim dari Padang-Lubuk Alung-Pariaman) adalah sebuah wilayah metropolitan di Provinsi Sumatera Barat yang m...

ąØą░čüčéčĆąŠąĄčćąĮčŗą╣ č鹥ą╗ąĄą▓ąĖąĘąĖąŠąĮąĮčŗą╣ čüąĖą│ąĮą░ą╗ ŌĆö čüą┐ąĄčåąĖą░ą╗čīąĮčŗą╣ čéąĖą┐ č鹥ą╗ąĄą▓ąĖąĘąĖąŠąĮąĮąŠą│ąŠ čüąĖą│ąĮą░ą╗ą░, čüą╗čāąČą░čēąĖą╣ čüčéą░ąĮą┤ą░čĆčéąĮąŠą╣ ą╝ąĄčĆąŠą╣ ą┐čĆąĖ ąĮą░čüčéčĆąŠą╣ą║ąĄ č鹥ą╗ąĄą▓ąĖąĘąĖąŠąĮąĮčŗčģ ą┐čĆąĖčæą╝ąĮąĖą║ąŠą▓. ąĪąĖą│ąĮą░ą╗čŗ ą│ąĄąĮąĄčĆąĖčĆčāčÄčéčüčÅ ąĖą╗ąĖ č鹥ą╗ąĄčåąĄąĮčéčĆą░ą╝ąĖ ą▓ č鹥čģąĮąŠą╗ąŠą│ąĖč湥čüą║ąĖčģ ą┐ą░čāąĘą░čģ ą▓ąĄčēą░ąĮąĖčÅ, ąĖą╗ąĖ ą┐ąŠčĆčéą░čéąĖą▓ąĮčŗą╝ąĖ ą│ąĄąĮąĄčĆą░č鹊čĆą░ą╝ąĖ čüąĖą│ąĮą░ą╗ą░. ąĪąŠą┤ąĄčƹȹ░ąĮąĖ

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Mal Ciputra Jakarta ŌĆō berita ┬Ę surat kabar ┬Ę buku ┬Ę cendekiawan ┬Ę JSTOR Mal Ciputra JakartaMal Ciputra JakartaLokasiTanjung Duren Utara, Grogol Petamburan, Jakarta Barat, Daerah Khusus Ibukota JakartaAla...

This is a list of members of the South Australian Legislative Council from 1843 to 1851.[1] Beginning with the Royal Instructions gazetted 15 June 1843, there were four official and four non-official members of the legislative council consisting of: the governor, colonial secretary, advocate-general, and registrar-General with four non-official members being nominated by the Crown.[1] The council was the only chamber of government until the House of Assembly was created in 185...

7-ąźą╗ąŠčĆąŠą║ąĖąĮčāčĆąĄąĮčüą║ą░ ą║ąĖčüąĄą╗ąĖąĮą░ ąØą░ąĘąĖą▓ąĖ IUPAC ąĮą░ąĘąĖą▓ 7-hloro-4-hidroksi-2-hinolinkarboksilna kiselina ąöčĆčāą│ąĖ ąĮą░ąĘąĖą▓ąĖ 7-CTKA ąśą┤ąĄąĮčéąĖčäąĖą║ą░čåąĖčśą░ 3ąö ą╝ąŠą┤ąĄą╗ (Jmol) ąĖąĮč鹥čĆą░ą║čéąĖą▓ąĮą░ čüą╗ąĖą║ą░ ChemSpider 1813 ECHA InfoCard 100.038.088 InChI InChI=1S/C10H6ClNO3/c11-5-1-2-6-7(3-5)12-8(10(14)15)4-9(6)13/h1-4H,(H,12,13)(H,14,15)ąÜčÖčāčć: UAWVRVFHMOSAPU-UHFFFAOYSA-N SMILES C1=CC2=C(C=C1Cl)N=C(C=C2O)C(=O)O ąĪą▓ąŠčśčüčéą▓ą░ ąźąĄą╝ąĖčśčüą║ą░ čä

Italian film and television actor (1924ŌĆō1984) For the comic book series, see Lupo Alberto. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Alberto Lupo ŌĆō news ┬Ę newspapers ┬Ę books ┬Ę scholar ┬Ę JSTOR (June 2019) (Learn how and when to remove this template message) Alberto LupoLupo in 1972BornAlberto Zoboli(1...

Dushanbe LambangNegara TajikistanPemerintahan ŌĆó Wali kotaMahmadsaid UbaydulloyevLuas ŌĆó Total124,6 km2 (481 sq mi)Ketinggian706 m (2,316 ft)Populasi (2008)[1] ŌĆó Total679.400Zona waktuUTC+5 (GMT) ŌĆó Musim panas (DST)UTC+5 (GMT)Situs webwww.dushanbe.tj Dushanbe (bahasa Tajik: ąöčāčłą░ąĮą▒ąĄ), adalah ibu kota Tajikistan. Nama kota ini berasal dari kata Persia yang bermakna Senin (du dua + shamba atau shanbe ...

Classic French sauce Duck a l'orange Bigarade sauce is an orange sauce prepared on the French dish duck ├Ī l'orange. It is based on the gastrique, a carmelized sugar mixed with white vinegar.[1] See also List of sauces References ^ Cooks Info: Sauce Bigarade. www.cooksinfo.com. Cooks Info. January 16, 2011. Retrieved June 9, 2022. vteCondiments List of condiments List of common dips List of syrups Sauces Agre dulce Agrodolce Aioli Barbecue sauce Bigarade sauce Brown sauce Buffalo sauc...

CouchSurfing ąōą░ą╗čāąĘčī ą┐čĆąŠą╝ąĖčüą╗ąŠą▓ąŠčüčéč¢ ą£ąĄčĆąĄąČą░ ą│ąŠčüčéąĖąĮąĮąŠčüčéč¢ ąöą░čéą░ čüčéą▓ąŠčĆąĄąĮąĮčÅŌĆ»/ŌĆēąĘą░čüąĮčāą▓ą░ąĮąĮčÅ 2 ą║ą▓č¢čéąĮčÅ 2003[1] ąŚą░čüąĮąŠą▓ąĮąĖą║ ąÜąĄą╣čüč¢ ążąĄąĮč鹊ąĮd ąÜčĆą░茹Įą░ ąĪą©ąÉ[2] ą×čĆą│ą░ąĮč¢ąĘą░čåč¢ą╣ąĮąŠ-ą┐čĆą░ą▓ąŠą▓ą░ č乊čĆą╝ą░ ą£ąĄčĆąĄąČą░ ą│ąŠčüčéąĖąĮąĮąŠčüčéč¢ č¢ C corporationd ąĀąŠąĘčéą░čłčāą▓ą░ąĮąĮčÅ čłčéą░ą▒-ą║ą▓ą░čĆčéąĖčĆąĖ ąĪą░ąĮ-ążčĆą░ąĮčåąĖčüą║ąŠ ą£ąŠą▓ą░ čéą▓ąŠčĆčā ą░ą▒ąŠ ąĮą░ąĘą▓ąĖ ą░ąĮą│ą╗č¢ą...

Ńé╗Ńā½Ńé▓ŃéżŃā╗Ńé©ŃāĢŃā¬ŃāźŃé╣ŃéŁŃā│ ÕÉŹÕēŹµ£¼ÕÉŹ Sergej EvljuskinŃéŁŃā½Ńé«Ńé╣Ķ¬× ąĪąĄčĆą│ąĄą╣ ąĢą▓ą╗čÄčüą║ąĖąĮÕ¤║µ£¼µāģÕĀ▒ÕøĮń▒Ź ŃāēŃéżŃāä ŃéŁŃā½Ńé«Ńé╣ńö¤Õ╣┤µ£łµŚź (1988-04-14) 1988Õ╣┤4µ£ł14µŚź’╝ł35µŁ│’╝ēÕć║Ķ║½Õ£░ ŃéĮŃāōŃé©ŃāłķĆŻķé” ŃéŁŃā½Ńé«Ńé╣Ńā╗ŃéĮŃāōŃé©ŃāłńżŠõ╝ÜõĖ╗ńŠ®Õģ▒ÕÆīÕøĮŃéóŃā¼Ńé»Ńé╗Ńé©ŃāĢŃé½’╝łĶŗ▒Ķ¬×ńēł’╝ēĶ║½ķĢĘ 187cmķüĖµēŗµāģÕĀ▒Õ£©ń▒ŹŃāüŃā╝ŃāĀ KSVŃāśŃāāŃé╗Ńā│Ńā╗Ńé½ŃāāŃé╗Ńā½ŃāØŃéĖŃéĘŃā¦Ńā│ DFĶāīńĢ¬ÕÅĘ 5Ńā”Ńā╝Ńé╣2003-2006 VfLŃā┤Ńé®Ńā½ŃāĢŃé╣Ńā¢Ńā½Ńé»Ńé»Ńā®Ńā¢1Õ╣┤ Ńé»Ńā®Ńā¢ Õć║ÕĀ┤ (ÕŠŚ

Russian general Gennady TarkhanovNative nameRussian: ąōąĄąĮąĮą░ą┤ąĖą╣ ąØąĖą║ąŠą╗ą░ąĄą▓ąĖčć ąóą░čĆčģą░ąĮąŠą▓ Azerbaijani: Gennadi Nikolayevi├¦ TarxanovBirth nameGennady Nikolaevich TarkhanovBorn(1854-09-08)September 8, 1854Russian EmpireDiedUnknownAllegiance Russian Empire (from 1871 to 1917) Azerbaijan Democratic Republic (from 1919 to 1920)Service/branchEngineeringYears of service1871 ŌĆö 1920Rank Lieutenant general of The Imperial Russian Army (from 1871 to 1909), head of the Engineeri...

┘éž▒┘Ŗž® ž©┘Ŗž¬ ┘ģž¬ž╣ - ┘éž▒┘Ŗž® - ž¬┘éž│┘Ŗ┘ģ žźž»ž¦ž▒┘Ŗ ž¦┘äž©┘äž» ž¦┘ä┘Ŗ┘ģ┘å ž¦┘ä┘ģžŁž¦┘üžĖž® ┘ģžŁž¦┘üžĖž® ž¦┘ä┘ģžŁ┘ł┘Ŗž¬ ž¦┘ä┘ģž»┘Ŗž▒┘Ŗž® ┘ģž»┘Ŗž▒┘Ŗž® ž¦┘äž▒ž¼┘ģ ž¦┘äž╣ž▓┘äž® ž╣ž▓┘äž® ž¦┘äž¼ž▒ž¦ž»┘Ŗ ž¦┘äž│┘āž¦┘å ž¦┘䞬ž╣ž»ž¦ž» ž¦┘äž│┘āž¦┘å┘Ŗ 2004 ž¦┘äž│┘āž¦┘å 78 ŌĆó ž¦┘äž░┘ā┘łž▒ 36 ŌĆó ž¦┘äžź┘垦ž½ 42 ŌĆó ž╣ž»ž» ž¦┘䞯ž│ž▒ 10 ŌĆó ž╣ž»ž» ž¦┘ä┘ģž│ž¦┘ā┘å 9 ┘ģž╣┘ä┘ł┘ģž¦ž¬ žŻž«ž▒┘ē ž¦┘䞬┘ł┘é┘Ŗž¬ ž¬┘ł┘é┘Ŗž¬ ž¦┘ä┘Ŗ┘ģ┘å (+3 ž║ž▒┘Ŗ┘å┘Ŗž¬ž┤) ž¬

┘ćž░┘ć ž¦┘ä┘ģ┘鞦┘äž® ┘Ŗž¬┘Ŗ┘ģž® žźž░ ž¬žĄ┘ä žź┘ä┘Ŗ┘枦 ┘ģ┘鞦┘䞦ž¬ žŻž«ž▒┘ē ┘é┘ä┘Ŗ┘äž® ž¼ž»┘ŗž¦. ┘üžČ┘ä┘ŗž¦žī ž│ž¦ž╣ž» ž©žźžČž¦┘üž® ┘łžĄ┘äž® žź┘ä┘Ŗ┘枦 ┘ü┘Ŗ ┘ģ┘鞦┘䞦ž¬ ┘ģž¬ž╣┘ä┘éž® ž©┘枦. (┘Ŗ┘ł┘ä┘Ŗ┘ł 2017) ┘åžĖž▒┘Ŗž® ž¦┘ä┘ģž©ž¦ž»ž” ž¦┘äžźž»ž¦ž▒┘Ŗž® ┘ć┘Ŗ ž¦┘ä┘åžĖž▒┘Ŗž® ž¦┘äžźž»ž¦ž▒┘Ŗž® ž¦┘䞬┘Ŗ ┘éž»┘ģ┘枦 ž¦┘äž╣ž¦┘ä┘ģ ž¦┘ä┘üž▒┘åž│┘Ŗ ┘ć┘åž▒┘Ŗ ┘üž¦┘Ŗ┘ł┘äžī ┘łž¦┘äž░┘Ŗ ž╣ž▒┘æ┘ü ž¦┘äžźž»ž¦ž▒ž® ž©┘é┘ł┘ä┘ć žŻ┘å ž¬┘ģž¦ž▒ž│ ž¦┘äžźž»ž¦ž▒ž® ┘ģž╣┘垦┘ć žŻ┘å ž¬ž¬┘åž©žŻ ┘łžŻ┘å ž¬ž«žĘžĘ ┘łžŻ┘å ž¬žĄž»ž▒ ž¦

River in Wisconsin, United StatesBois Brule RiverBois Brule River near Winneboujou, WisconsinLocationCountryUnited StatesLocationDouglas County, WisconsinPhysical characteristicsSource • elevation600 ft (180 m) Mouth • locationLake Superior • coordinates46┬░24ŌĆ▓10ŌĆ│N 91┬░44ŌĆ▓38ŌĆ│W / 46.4027187┬░N 91.7438003┬░W / 46.4027187; -91.7438003Length43.9 mi (70.7 km)Basin featuresGNIS1...

Grotte du GazelLocalisationCoordonn├®es 43┬░ 19ŌĆ▓ 33ŌĆ│ N, 2┬░ 25ŌĆ▓ 17ŌĆ│ EPays FranceR├®gion Languedoc-Roussillon (Occitanie)D├®partement AudeCommune Sall├©les-Cabard├©sMassif Montagne Noire (versant sud)Vall├®e ruisseau d'Escole (Ceize)Caract├®ristiquesAltitude de l'entr├®e ~275 mP├®riode de formation Cambrien inf├®rieurOccupation humaine Magdal├®nien final, LaborienPatrimonialit├® Class├® MH (1948)Localisation sur la carte de FranceLocalisation su...

Aleksandr Vladimirovich Dvornikov (bahasa Rusia : ąÉą╗ąĄą║čüą░ąĮą┤čĆ ąÆą╗ą░ą┤ąĖą╝ąĖčĆąŠą▓ąĖčć ąöą▓ąŠčĆąĮąĖą║ąŠą▓ ; lahir 22 Agustus 1961) adalah seorang jenderal angkatan darat Rusia yang memimpin intervensi militer Rusia di Suriah dan invasi Rusia ke Ukraina.Aleksandr DvornikovAleksandr Dvornikov Tahun 2021Nama asliąÉą╗ąĄą║čüą░ąĮą┤čĆ ąÆą╗ą░ą┤ąĖą╝ąĖčĆąŠą▓ąĖčć ąöą▓ąŠčĆąĮąĖą║ąŠą▓Lahir22 Agustus 1961 (umur 62)Ussuriysk, RSFS Rusia, Uni SovietPengabdian Uni Soviet RusiaDi...

Ini adalah daftar katedral di Inggris. Katolik Gereja Latin Provinsi Westminster Gambar Nama dan dedikasi Keuskupan Didirikan, lokasi Katedral BrentwoodGereja Katedral Santa Maria dan Santa Helena Keuskupan Brentwood 1917 gereja paroki sejak 1861 51┬░37ŌĆ▓11ŌĆ│N 0┬░18ŌĆ▓24ŌĆ│E / 51.619625┬░N 0.306560┬░E / 51.619625; 0.306560 (Brentwood Cathedral) Katedral NorwichGereja Katedral Santo Yohanes Pembaptis Keuskupan Anglia Timur 1976 52┬░37ŌĆ▓45ŌĆ│N 1┬░17ŌĆ▓02ŌĆ│E&#...

This article is about the district. For its eponymous headquarters, see Alwar. District of Rajasthan in IndiaAlwar districtDistrict of RajasthanClockwise from top-left: Alwar fort, Musi Maharani ki Chhatri, Neelkanth Shiv Mandir, Sariska Tiger Reserve, Bhangarh FortLocation of Alwar district in RajasthanCoordinates (Alwar): 27┬░34ŌĆ▓12ŌĆ│N 76┬░36ŌĆ▓00ŌĆ│E / 27.57000┬░N 76.60000┬░E / 27.57000; 76.60000Country IndiaStateRajasthanDivisionJaipurHeadquartersAlwarTe...

Figure-eight-shaped curve This article is about figure-eight shaped curves in algebraic geometry. For other uses, see Lemniscate (disambiguation). The lemniscate of Bernoulli and its two foci In algebraic geometry, a lemniscate is any of several figure-eight or Ōł×-shaped curves.[1][2] The word comes from the Latin l─ōmnisc─ütus meaning decorated with ribbons,[3] from the Greek ╬╗╬Ę╬╝╬Į╬»Žā╬║╬┐Žé meaning ribbon,[2][4][5][6] or which alte...

Railway station in Kiruna, Sweden The former Kiruna Central Station Kiruna Central Station (Swedish: Kiruna centralstation) is a railway station located on the Iron Ore Line in Kiruna, Sweden. The station is served by up to three daily services northwards on the Iron Ore Line to Narvik Station in Norway. Southwards, the station is served by two daily services to Lule├ź Central Station and Stockholm Central Station, operated by SJ, and two (week-ends) or three (weekdays) daily services to Lule...