Théorème de Feit-Thompson
|
Read other articles:

HansTokoh FrozenPenampilanperdanaFrozen (2013)PenciptaChris BuckJennifer LeePengisi suaraSantino FontanaInformasiAliasHans Westergaard[1]GelarPangeran Kepulauan selatanPekerjaanWali raja Arendelle (jangka pendek)KerabatDua belas kakak, orangtua Pangeran Hans dari Kepulauan Selatan, juga dikenal sebagai Hans Westergaard, adalah sebuah karakter fiksi sekaligus tokoh antagonis utama dari film animasi Walt Disney Animation Studios ke-53, Frozen. Pengisi suaranya adalah Santino Fontana. Re...

The Cross of Mathildel 中世のカトリック教会は教会国家という世俗的な基盤を有しながらも、全ヨーロッパ規模での普遍的な権威を主張した。近代ヨーロッパ各地に国民国家が成立していくと教皇領は世俗国家に回収された。現在ローマ教皇庁は独立国家バチカン市国にある。 中世ヨーロッパ史においては、西欧諸国の学界においても日本の学界においても「教会と国家」と

اتفاقية فيصل وايزمانمعلومات عامةالنوع معاهدة الموقعون الحسين بن علي — حاييم وايزمان تعديل - تعديل مصدري - تعديل ويكي بيانات خريطة تبين حدود الدولة اليهودية التي تقرر إنشاءها في إتفاقية فيصل وايزمان في مؤتمر باريس للسلام 1919م،والمسميات اليهودية لمناطق الدولة اليهودية ومد�...

黃正銘 黄正铭(1903年10月2日—1973年5月23日),字君白,浙江省宁海县城东门人。中华民国法学家、法官。[1] 生平 黄正铭最初入柏屏学堂学习,后来入宁海县立正学高等小学堂,此后入宁波的浙江省立第四中学。毕业后,到正学小学堂担任英语教师。民国13年(1924年),考入南京国立东南大学政治系。毕业获得法学士学位。后来,参加浙江省选拔县长考试,取得第一�...

French painter, from the Fauvist movement Not to be confused with Albert Marque. Albert MarquetSelf-Portrait Albert Marquet, 1904BornPierre-Albert Marquet(1875-03-27)27 March 1875Bordeaux, Gironde, FranceDied14 June 1947(1947-06-14) (aged 72)La Frette-sur-Seine, Val-d'Oise, FranceEducationEcole des Arts Decoratifs, École des Beaux-Arts, Gustave MoreauKnown forPaintingMovementFauvism Albert Marquet, 1906, Fécamp (The Beach at Sainte-Adresse), oil on canvas, 64.5 x 80 cm Albert Marq...
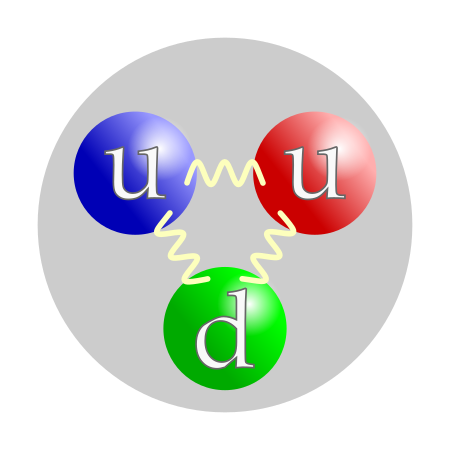
Particle smaller than an atom A composite particle proton is made of two up quark and one down quark, which are elementary particles. In physics, a subatomic particle is a particle smaller than an atom.[1] According to the Standard Model of particle physics, a subatomic particle can be either a composite particle, which is composed of other particles (for example, a baryon, like a proton or a neutron, composed of three quarks; or a meson, composed of two quarks), or an elementary part...

本列表是河南省南阳市的文物保护单位的集合。南阳市是著名的历史文化名城,建城史三千多年,有众多的名胜古迹。 现拥有国家级重点文物保护单位12处,河南省重点文物保护单位百余处,文物资源十分丰富。 世界自然文化遗产 南阳伏牛山世界地质公园 西峡恐龙蛋(骨骼)化石群 国家级重点文物保护单位 第三批 1988年11月13日公布 医圣祠(东汉)南阳市区 山陕会馆(清朝�...

日語寫法日語原文慶長假名けいちょう平文式罗马字Keichō 慶長是一個日本年號,接在文禄之後,元和之前。即公元1596年到1615年為止之間。這時代的天皇是後陽成天皇、後水尾天皇[1] 。天下人是時任太閤的豐臣秀吉與後繼的幼子豐臣秀賴。江戶幕府的將軍是德川家康、德川秀忠。 改元 文禄五年十月二十七日(公曆1596年12月16日),災難、異象頻生,故此改元。 慶長�...

Species of bird Philippine pitta Illustration by Nicolas Huet Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Passeriformes Family: Pittidae Genus: Erythropitta Species: E. erythrogaster Binomial name Erythropitta erythrogaster(Temminck, 1823) Synonyms Pitta erythrogaster The Philippine pitta (Erythropitta erythrogaster) or blue-breasted pitta, is a species of bird in the family...

Netflix is a subscription streaming service owned by the American company Netflix, Inc. Launched on August 29, 1997, it initially offered DVD rental and sale by mail, but the sales were eliminated within a year to focus on the DVD rental business. In 2007, the company began transitioning to its current subscription streaming model. Since its launch, the company has been subject to numerous criticisms, the basis of which range from its business practices and workplace culture to issues with th...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2023. Outerbloom adalah sebuah perusahaan yang bergerak di bidang penyediaan rangkaian bunga, parsel, bingkisan, serta berbagai keperluan hadiah. Sejarah Outerbloom didirikan pada tahun 2016 oleh William Tunggaldjaja. Selain menawarkan layanan daring melalui...

Television series Not to be confused with The Red Skelton Program. The Red Skelton ShowRed Skelton and Mickey Rooney at dress rehearsal for The Red Skelton Show at studio 33, January 15, 1957.Also known asThe Red Skelton HourGenreVarietyDirected bySeymour BernsJack DonohueJohn GauntEd HillerBill HobinTerry KyneHoward A. QuinnMartin RackinPresented byRed SkeltonVoices ofArt GilmoreTheme music composerDavid RoseOpening themeHoliday for Strings.[1](Date of Registration with U.S. Copyrigh...

Urszula Radwańska Urszula Radwańska nel 2016 Nazionalità Polonia Altezza 177 cm Peso 57 kg Tennis Carriera Singolare1 Vittorie/sconfitte 393 - 312 (55.74%) Titoli vinti 0 WTA, 7 ITF Miglior ranking 29º (8 ottobre 2012) Ranking attuale 278ª (7 marzo 2022) Risultati nei tornei del Grande Slam Australian Open 2T (2012) Roland Garros 2T (2012, 2013) Wimbledon 2T (2008, 2009, 2013, 2015) US Open 2T (2010, 2013) Altri tornei Giochi olimpici 2T (2012) Doppio1...

Nigerian music video director (born 1987) Unlimited L.ABackground informationBirth nameBuari Olalekan OluwasegunBorn (1987-04-02) 2 April 1987 (age 36)[1]Lagos, NigeriaOccupation(s)cinematographer, editor, colorist, music video directorYears active2011 - presentMusical artist Buari Olalekan Oluwasegun (born 2 April 1987; professionally known as Unlimited L.A) is a Nigerian music video director.[2][3][4] He has worked with several musical genres and artists...

1990 single by Marty StuartHillbilly RockSingle by Marty Stuartfrom the album Hillbilly Rock B-sideWestern GirlsReleasedMarch 1990GenreCountry rock, rockabillyLength2:38LabelMCASongwriter(s)Paul KennerleyProducer(s)Richard Bennett, Tony BrownMarty Stuart singles chronology Don't Leave Her Lonely Too Long (1990) Hillbilly Rock (1990) Western Girls (1990) Hillbilly Rock is a song written by Paul Kennerley, and recorded by American country music artist Marty Stuart. It was released in March 1990...

2020 Wisconsin Democratic presidential primary 2020 Wisconsin Democratic presidential primary ← 2016 April 7, 2020 2024 → ← ILAK →97 delegates (84 pledged, 13 unpledged)to the Democratic National ConventionThe number of pledged delegates won is determined by the popular vote Candidate Joe Biden Bernie Sanders Home state Delaware Vermont Delegate count 56 28 Popular vote 581,463 293,441 Percentage 62.9% 31.7% Election results by...

British-bred Thoroughbred racehorse Jack HornerGrand National (1926, Aintree)SireCylliusGrandsireCylleneDamMeltons GuideDamsireMeltonSexGeldingFoaled1917CountryUnited KingdomColourChestnutBreederJohn MuskerOwnerCharles SchwartzTrainerHarvey LeaderMajor winsGrand National (1926) Jack Horner (foaled 1917 by Cyllius out of Meltons Guide) was a British Thoroughbred race horse who won the 1926 Grand National. Background A week before the Grand National Mr. A.C. Schwartz bought Jack Horner for 5,00...
Process of increasing reproductive isolation Not to be confused with Secondary contact. Reinforcement assists speciation by selecting against hybrids upon the secondary contact of two separated populations of a species. Part of a series onEvolutionary biologyDarwin's finches by John Gould Index Introduction Main Outline Glossary Evidence History Processes and outcomes Population genetics Variation Diversity Mutation Natural selection Adaptation Polymorphism Genetic drift Gene flow Speciation ...

틴 팝 (Teen pop)장르 뿌리팝[1]버블검 팝[2]신스팝[3]댄스 팝[1]R&B[4]어반 컨템포러리[1]문화 뿌리1940년-1990년, 미국, 영국[1]사용 악기 드럼 머신 일렉트로닉 드럼 드럼 신디사이저 때때로 키보드 보컬 오토튠 기타 베이스 기타 파생 장르유로팝퓨전 장르어덜트 컨템포러리지역별 장르올랜도[5] 로스앤젤레스관련 항목 보이 밴드 �...

Girl CrazyEnghraifft o'r canlynolffilm Lliw/iaudu-a-gwyn GwladUnol Daleithiau America Dyddiad cyhoeddi1943 Genrecomedi ramantus, ffilm gerdd Lleoliad y gwaithCaliffornia Hyd99 munud CyfarwyddwrNorman Taurog, Busby Berkeley Cynhyrchydd/wyrArthur Freed Cwmni cynhyrchuMetro-Goldwyn-Mayer CyfansoddwrGeorge Gershwin DosbarthyddMetro-Goldwyn-Mayer, Netflix Iaith wreiddiolSaesneg SinematograffyddWilliam H....






