Geometric Brownian motion
|
Read other articles:

Приготування арахісової пасти Пізня вечеря в Бісау Кухня Гвінеї-Бисау почасти визначається географією, історією та економікою цієї країни. Так, основою харчування мешканців узбережжя є рис, а у віддалених від Атлантичного океану регіонах — пшоно. Велика частина рису...

Untuk perusahaan perkeretaapian di Indonesia bernama PT Kereta Api Indonesia (Persero), lihat Kereta Api Indonesia. Kereta api penumpang kelas eksekutif. Kereta api barang angkutan kontainer. Kereta rel listrik komuter. Kereta api (bahasa Inggris: train) adalah bentuk pengangkutan rel yang terdiri dari serangkaian kendaraan yang ditarik sepanjang jalur kereta api untuk mengangkut kargo atau penumpang. Gaya gerak disediakan oleh lokomotif yang terpisah atau motor individu dalam beberapa un...

Franz Xaver Schwarz Franz Xaver Schwarz (* 27. November 1875 in Günzburg; † 2. Dezember 1947 im Internierungslager bei Regensburg) war ein deutscher Politiker der NSDAP. Schwarz war als „Reichsschatzmeister der NSDAP“ (Reichsleiter) und SS-Oberst-Gruppenführer einer der wichtigsten Funktionäre der Partei. Inhaltsverzeichnis 1 Leben 1.1 Frühes Leben 1.2 Laufbahn in der NSDAP 1.3 Nachkriegszeit 2 Ehe und Familie 3 Schriften 4 Literatur 5 Weblinks 6 Einzelnachweise Leben Frühes Leben ...

Stasiun Uzen-Nakayama羽前中山駅Bangunan baru Stasiun Uzen-Nakayam pada Agustus 2005Lokasi3590, Nakayama, Kaminoyama-shi, Yamagata-ken 999-3246JepangKoordinat38°07′28″N 140°13′06″E / 38.124467°N 140.218375°E / 38.124467; 140.218375Koordinat: 38°07′28″N 140°13′06″E / 38.124467°N 140.218375°E / 38.124467; 140.218375Pengelola JR EastJalur■ Jalur Utama ŌuLetak dari pangkal68.3 km dari FukushimaJumlah peron2 peron sisiI...

瀑布基本资料导演鍾孟宏监制曾少千瞿友寧董成瑜制片廖世芳瞿友寧董成瑜王亭坤張承宏梁宏志编剧鍾孟宏張耀升主演賈靜雯王淨配乐盧律銘摄影鍾孟宏剪辑賴秀雄制片商本地風光電影氧氣電影鏡文學三皇生物科技百聿數碼創意華映娛樂片长129分鐘产地 臺灣语言華語上映及发行上映日期 2021年9月6日 (2021-09-06)(威尼斯影展) 2021年9月13日 (2021-09-13)(多倫多影展) 2021�...

68-ма армія СРСРНа службі 1 лютого — 5 листопада 1943Країна СРСРНалежність Північно-Західний фронт Резерв Ставки ВГК Західний фронтВид Червона арміяТип сухопутні військаРоль загальновійськоваЧисельність арміяВійни/битви Німецько-радянська війнаСмоленська операція (1...

No debe confundirse con WWE Women's Championship el campeonato antiguo. No debe confundirse con WWE Women's Championship el campeonato femenino de SmackDown. Women's World ChampionshipNombre Campeonato Mundial FemeninoPromoción WWEMarca RawReinados oficiales 26Campeón actual Rhea RipleyFecha de obtención 1 de abril de 2023Fecha de creación 23 de agosto de 2016Primer campeón Becky LynchOtros nombres WWE SmackDown Women's Championship(2016-2023) Women's World Championship(2023-presente) &#...

British Army general Julian HaslerBorn(1868-10-16)16 October 1868Aldingbourne House, ChichesterDied27 April 1915(1915-04-27) (aged 46)Ypres, BelgiumAllegianceUnited KingdomService/branchBritish ArmyYears of service1888–1915RankBrigadier-GeneralUnitEast Kent RegimentCommands held11th Infantry BrigadeBattles/warsSouth African WarFirst World WarAwardsMention in DispatchesRelationsWilliam Wyndham Hasler (father) Brigadier-General Julian Hasler (16 October 1868 – 27 April 1915), was ...

American basketball player (born 1980) Caron ButlerButler with the Washington Wizards in 2007Miami HeatPositionAssistant coachLeagueNBAPersonal informationBorn (1980-03-13) March 13, 1980 (age 43)Racine, Wisconsin, U.S.Listed height6 ft 7 in (2.01 m)Listed weight228 lb (103 kg)Career informationHigh school Racine Park (Racine, Wisconsin) Maine Central Institute(Pittsfield, Maine) CollegeUConn (2000–2002)NBA draft2002: 1st round, 10th overall pickSelected by the...

American historian This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Aviva Chomsky – news · newspapers · books · scholar · JSTOR (November 2017) (Learn how and when to remove this template message...

Line of tablet computers by Apple This article is about the line of devices. For the first device marketed with this name, see iPad Mini (1st generation). For the device currently marketed with this name, see iPad Mini (6th generation). Not to be confused with iPod Mini. iPad miniDeveloperApple Inc.ManufacturerFoxconn, Pegatron[1]Product familyiPadTypeTablet computerRelease dateNovember 2, 2012; 11 years ago (2012-11-02) (1st generation)Units sold600 millionOperating...

2010 video game 2010 video gameScott Pilgrim vs. The World: The GameForeground: Scott Pilgrim; Background, upper left: Stephen Stills; Lower left: Kim Pine; bottom: Ramona FlowersDeveloper(s)Ubisoft MontrealUbisoft Chengdu[a]Publisher(s)UbisoftDirector(s)Lei YuProducer(s)Caroline MartinDesigner(s)Jonathan LavigneZhu Bi JiaYan KaiJiang An QiOu Yue SongProgrammer(s)WeiKe ZengArtist(s)Paul RobertsonStéphane BoutinJonathan LavigneJustin CyrJonathan KimMariel CartwrightComposer(s)Anamanag...

Australian scientist Stephen SimpsonAC FRS FAABorn26 June 1957 Alma materUniversity of QueenslandKing's College LondonAwardsAustralian Laureate Fellowship (2009) Websitewww.sydney.edu.au/science/about/our-people/academic-staff/stephen-simpson.htmlAcademic careerFieldsEntomology, nutrition InstitutionsObesity AustraliaCharles Perkins Centre Stephen James Simpson AC[2] FRS FAA (born 26 June 1957)[1] is the executive director of Obesity Australia and the academic d...
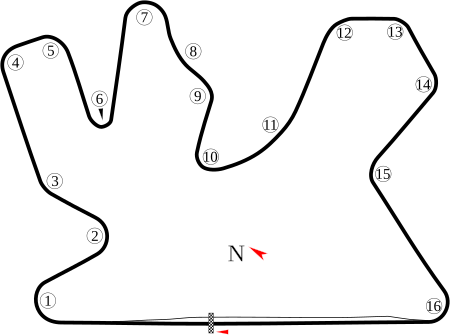
2009 Qatar Grand PrixRace detailsRace 1 of 17 races in the2009 Grand Prix motorcycle racing seasonDate12–13 April 2009Official nameCommercialbank Grand Prix of Qatar[1]LocationLosail International CircuitCoursePermanent racing facility5.380 km (3.343 mi)MotoGPPole positionRider Casey StonerTime 1:55.286Fastest lapRider Casey StonerTime 1:55.844PodiumFirst Casey StonerSecond Valentino RossiThird Jorge Lorenzo250 ccPole positionRider Álvaro BautistaTime 2:00.677...

Marksman On Mark Marksman C N60XX fitted with deepened pressurised fuselage, R-2800 engines and wing tip tanks Role Executive transportType of aircraft Manufacturer On Mark Engineering First flight January 1961[1] Introduction 1961 Produced 1961–1964 Number built 8[2] Developed from Douglas A-26 Invader The On Mark Marksman was an American high-speed civil executive aircraft converted from surplus Douglas A-26 Invader airframes by On Mark Engineering. Its antecedents wer...

Fast food chain Hartz ChickenTrade nameHartz Chicken BuffetTypePrivateIndustryFoodFounded1972; 51 years ago (1972) in Texas, United StatesFounderW. Lawrence Hartzog Sr.HeadquartersSpring, Texas, United StatesArea servedNorth America, MalaysiaProductsFast food, including fried chicken, french fries, yeast rolls, fried fish and salads, hot vegetables, hot soup and ice-cream.OwnerHartz Franchise Restaurants, LtdWebsitehartz-chicken.com Hartz Chicken (also known as Hartz Chicken...

For the match on June 8, 2017, see 2018 FIFA World Cup qualification – CONCACAF fifth round § United States v Trinidad and Tobago. Football matchTrinidad and Tobago v United States (2017)Ato Boldon Stadium hosted the matchEvent2018 FIFA World Cup qualification – CONCACAF fifth round Trinidad and Tobago United States 2 1 Panama qualifies for the 2018 FIFA World Cup Honduras advances to the CONCACAF–AFC inter-confederation play-off United States fails to qualify for the World Cup fo...

For the political alliance in Kerala, see United Democratic Front (Kerala). United Democratic Front is a front of eight political parties (Mizo National Front, Mizoram People's Conference, Zoram Nationalist Party, Maraland Democratic Front, Hmar People's Convention, Paite Tribes Council, Bharatiya Janata Party, and Nationalist Congress Party) in the Indian state of Mizoram.[1] The front fielded Robert Romawia Royte for Mizoram's lone Lok Sabha constituency in the 2014 Indian general e...

Witold Lutosławski nel 1993 Witold Lutosławski (Varsavia, 25 gennaio 1913 – Varsavia, 7 febbraio 1994) è stato un compositore e direttore d'orchestra polacco, uno dei maggiori compositori europei del XX secolo, e uno dei più importanti musicisti polacchi degli ultimi decenni. Lutoslawski fu studente del famoso professore Witold Maliszewski (1873 - 1939). Fu autore sensibile alla tradizione polacca quanto allo sperimentalismo dell'avanguardia viennese non rinnegando alcuni lasciti inelud...

Historic district in Michigan, United States United States historic placeGrand Circus Park Historic DistrictU.S. National Register of Historic PlacesU.S. Historic district Looking southwestLocationDetroit, Michigan, U.S.Coordinates42°20′10″N 83°3′2″W / 42.33611°N 83.05056°W / 42.33611; -83.05056Built1867NRHP reference No.83000894; 00001488 (boundary increase)[1]Added to NRHPFebruary 28, 1983; December 07, 2000 (boundary increase); December...



























![{\displaystyle \operatorname {E} \left[\exp \left(2\sigma W_{t}-\sigma ^{2}t\right)\mid {\mathcal {F}}_{s}\right]=e^{\sigma ^{2}(t-s)}\exp \left(2\sigma W_{s}-\sigma ^{2}s\right),\quad \forall 0\leq s<t.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/121f4efbdcac966a20535657392d5de0345d6f9b)

![{\displaystyle {\partial p \over {\partial t}}+{\partial \over {\partial S}}[\mu (t,S)p(t,S)]={1 \over {2}}{\partial ^{2} \over {\partial S^{2}}}[\sigma ^{2}(t,S)p(t,S)],\quad p(0,S)=\delta (S)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4aead5a9293ecf1973cba7b9b8683d2ded50d1f)











![{\displaystyle p(t,S)={1 \over {S{\sqrt {2\pi \sigma ^{2}t}}}}\exp \left\{-{\left[\log(S/S_{0})-\left(\mu -{1 \over {2}}\sigma ^{2}\right)t\right]^{2} \over {2\sigma ^{2}t}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26797fa1b6e421209c7314318b486e26694d685)
![{\displaystyle {\begin{alignedat}{2}d\log(S)&=f'(S)\,dS+{\frac {1}{2}}f''(S)S^{2}\sigma ^{2}\,dt\\[6pt]&={\frac {1}{S}}\left(\sigma S\,dW_{t}+\mu S\,dt\right)-{\frac {1}{2}}\sigma ^{2}\,dt\\[6pt]&=\sigma \,dW_{t}+(\mu -\sigma ^{2}/2)\,dt.\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b72bd76b7255e8dbd8e7c224df8ec2ac15ba9d)

![{\displaystyle {\begin{alignedat}{2}\log(S_{t})&=\log \left(S_{0}\exp \left(\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}\right)\right)\\[6pt]&=\log(S_{0})+\left(\mu -{\frac {\sigma ^{2}}{2}}\right)t+\sigma W_{t}.\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/592321ca2ac7a8f230e2854bef22804a8c3d1064)









