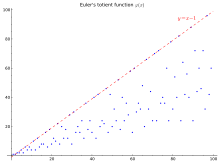
Fungsi phi Euler
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Surili sarawak Presbytis chrysomelas Status konservasiTerancam kritisIUCN39803 TaksonomiKerajaanAnimaliaFilumChordataKelasMammaliaOrdoPrimatesFamiliCercopithecidaeGenusPresbytisSpesiesPresbytis chrysomelas Müller, 1838 Distribusi lbs Surili sarawak (P...

Gunung Senjō (仙丈ヶ岳code: ja is deprecated , Senjou-ga-take) adalah gunung setinggi 3.032 m (9.948 ft).[1] Gunung ini berada di perbatasan kota Minami-Alps, Yamanashi, dan Ina, Nagano, di Jepang. Gunung ini adalah salah satu puncak utama dari Pegunungan Akaishi, dan merupakan salah satu puncak paling populer di daerah ini. Gunung ini juga merupakan salah satu dari 100 Pegunungan yang Terkenal di jepang. Gunung Senjō仙丈ヶ岳Gunung Senjō dilihat dari Gunung Ko-Sen...

Japanese department for military and national security Ministry of Defense防衛省Bōei-shōAgency overviewFormed9 January 2007; 16 years ago (2007-01-09)Preceding agencyDefense AgencyJurisdictionGovernment of JapanHeadquarters5-1 Ichigaya-honmuracho, Ichigaya, Shinjuku-ku, Tokyo, JapanEmployees20,924 civilian staff[1]247,154 SDF personnel (Excluding non-capacity National Defense Academy students, SDF reserve personnel, ready reserve SDF personnel, etc.)[2]A...

Maiensäss Matschwitz im Montafon (ca. 1905) Häuser in Matschwitz; Richtung Golmerbahn (2005) Das Maiensäss (bzw. Maiensäß), auch Maisäss (Maisäß), Maien, Vorsäss (Vorsäß), Hochsäß, Niederleger, Unterstafel, in Graubünden auch rätoromanisch acla,[1] im Tessin Monti,[2] im Unterwallis frankoprovenzalisch Mayens, ist eine Sonderform der Alm/Alp: eine gerodete Fläche mit Hütten und Ställen. Auf jedem Maiensäss steht mindestens ein kleines Haus und ein Stall; als...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2019) ستيفاني باتون معلومات شخصية الميلاد سنة 1969 (العمر 53–54 سنة) نيو أورلينز مواطنة الولايات المتحدة[1] الحياة العملية المهنة رسامة، وفنانة...

Ayumi BeppuLahir14 Juni 1983 (umur 40)SakaiTahun aktif2005-sekarang Ayumi Beppu (別府 あゆみcode: ja is deprecated , Beppu Ayumi, lahir 14 Juni 1983) adalah aktris asal Jepang. Julukannya adalah Beppy (べっぴぃcode: ja is deprecated , Beppii). Ia dikenal dengan peran-perannya dalam serial tokusatsu dan drama: sebagai Houka Ozu / MagiPink dalam serial Super Sentai Mahou Sentai Magiranger, dan sebagai Ayumiko Kitabeppu / Detektif Angkasa Wanita Beppy dalam Chou Ninja Tai Inaz...

Amien Rais, pembentuk Poros Tengah Poros Tengah adalah istilah yang mengacu kepada koalisi partai-partai Islam yang dibentuk setelah Partai Demokrasi Indonesia-Perjuangan (PDI-P) memenangkan pemilihan umum legislatif Indonesia 1999. Sebelumnya, pada Juni 1999, PDI-P telah memenangkan pemilihan umum dengan persentase 33%. Mengingat bahwa presiden dipilih oleh Sidang Umum Majelis Permusyawaratan Rakyat (MPR) pada masa itu, Megawati diperkirakan akan menjadi presiden. Namun, pada 7 Oktober 1999,...

Церковь (Коморни Лхотка) Силезская евангелическая церковь Аугсбургского исповедания — лютеранская община Чехии польского происхождения. Основана в 1920 после распада Австро-Венгрии на базе польских лютеранских общин. С 1938 по 1948 находилась либо на нелегальном положен�...

NGC 5261 الكوكبة العذراء[1] رمز الفهرس NGC 5261 (الفهرس العام الجديد)PGC 48360 (فهرس المجرات الرئيسية)2MASX J13401609+0504343 (Two Micron All Sky Survey, Extended source catalogue)Z 45-67 (فهرس المجرات وعناقيد المجرات)UZC J134016.1+050435 (فهرس زفيكي المحدّث)Z 1337.7+0519 (فهرس المجرات وعناقيد المجرات)NPM1G +05.0394 (Lick Northern Proper Motion Surv...

Town in Burgas, Bulgaria Place in Burgas, BulgariaMalko Tarnovo Малко Търново Coat of armsMalko TarnovoLocation of Malko TarnovoCoordinates: 41°59′N 27°32′E / 41.983°N 27.533°E / 41.983; 27.533Country BulgariaProvince(Oblast)BurgasGovernment • MayorIliyan YanchevElevation348 m (1,142 ft)Population (December 2009)[1] • Total2,449Time zoneUTC+2 (EET) • Summer (DST)UTC+3 (EEST)Postal Code8...

Alstom Prima II on display at InnoTrans 2014 in Berlin Prima is a family of railway diesel and electric locomotives built by Alstom. During the late 1990s, manufacture of the type had commenced; by 2008, Alstom had reportedly sold 1,750 Prima locomotives.[citation needed] In 2009, the second generation Prima II was launched.[1] During 2013, the Prima H3 diesel/battery hybrid locomotive was launched. First generation This section needs expansion. You can help by adding to it. (...

Oversees the operation of New England's bulk electric power system This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: ISO New England – news · newspapers · books · scholar · JSTOR (October 2021) (Learn how and when to remove this template message) ISO New EnglandFounded19972005 (designated RTO)TypeNon profit, i...

2005 studio album by SubArachnoid SpaceThe Red VeilStudio album by SubArachnoid SpaceReleasedFebruary 15, 2005RecordedApril 2004GenreSpace rock, psychedelic rockLength40:15LabelStrange Attractors Audio HouseProducerMason Jones, Donny Newenhouse, SubArachnoid SpaceSubArachnoid Space chronology Also Rising(2003) The Red Veil(2005) Eight Bells(2009) Professional ratingsReview scoresSourceRatingAllmusic[1] The Red Veil is the fifth studio album by SubArachnoid Space, released on F...

Miracle attributed to Muhammad, in which the Moon was split in two This article is about an Islamic theological issue. For theories of formation of the Moon which involve fragments, see Origin of the Moon § Accretion. Muhammad points out the splitting of the Moon. Anonymous 16th-century watercolor from a falnama, a Persian book of prophecy. Muhammad is the veiled figure on the right. Part of a series onMuhammad Life Mecca Hijrah Medina After Conquest of Mecca Farewell Pilgrimage (Farewe...

Finance property of an asset For other uses, see Liquidity (disambiguation). In business, economics or investment, market liquidity is a market's feature whereby an individual or firm can quickly purchase or sell an asset without causing a drastic change in the asset's price. Liquidity involves the trade-off between the price at which an asset can be sold, and how quickly it can be sold. In a liquid market, the trade-off is mild: one can sell quickly without having to accept a significantly l...

Lion and tigress hybrid For other uses, see Liger (disambiguation). Liger Female (left) and male ligers at Everland amusement park in South Korea Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Carnivora Suborder: Feliformia Family: Felidae Subfamily: Pantherinae Genus: Panthera Species: P. leo♂ × P. tigris♀ The liger is a hybrid offspring of a male lion (Panthera leo) and a tigress, or female tiger (Panthera tigris). The liger h...

TethymyxineTemporal range: Cenomanian PreꞒ Ꞓ O S D C P T J K Pg N Reconstruction with Scapanorhynchus Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Infraphylum: Agnatha Class: Myxini Order: Myxiniformes Family: Myxinidae Genus: †TethymyxineMiyashita et al., 2019 Species: †T. tapirostrum Binomial name †Tethymyxine tapirostrumMiyashita et al., 2019 Tethymyxine is an extinct genus of hagfish known from the Late Cretaceous (Cenomanian) of Le...

Спутниковый телефон Inmarsat на индонезийском острове Ниас после землетрясения в 2005 году Варианты спутниковых телефонов Спу́тниковый телефо́н — мобильный телефон, передающий информацию напрямую через специальный коммуникационный спутник. В зависимости от оператора с...

Extinct genus of reptiles AraripesuchusTemporal range: Early - Late Cretaceous, 125–66 Ma PreꞒ Ꞓ O S D C P T J K Pg N Skull of A. wegeneri from different angles Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Reptilia Clade: Pseudosuchia Clade: Crocodylomorpha Suborder: †Notosuchia Family: †Uruguaysuchidae Genus: †AraripesuchusPrice, 1959 Species †A. gomesii Price, 1959 (type) †A. wegeneri Buffetaut, 1981 †A. patagonicus Ortega et a...

Slovenian actor This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Klemen Slakonja – news · newspapers · books · scholar · JSTOR (March 2022) (Learn how and when to remove this template message) Kl...