Квадратний корінь
| |||||||||||||||||||||||||||||||
Read other articles:

مانويل إنريكي اروجو معلومات شخصية الميلاد 12 أكتوبر 1865(1865-10-12)أليغريا [لغات أخرى] الوفاة 9 فبراير 1913 (47 سنة)سان سلفادور مكان الدفن سان سلفادور مواطنة السلفادور مناصب عمدة سان سلفادور[1] في المنصب1 يناير 1888 – 31 ديسمبر 1888 أستاذ جامعي[2] تول

Governing body of football in Guinea Guinean Football FederationCAFFounded1959[1]HeadquartersConakryFIFA affiliation1962CAF affiliation1962[2]PresidentMolokai WesleyWebsitehttp://www.feguifoot.com/ The Guinean Football Federation (French: Fédération Guinéenne de Football, FGF) is the governing body of football in Guinea. It was founded in 1959, affiliated to FIFA and to CAF in 1962. It organizes the national football league and the national team, which has never qualified f...

Para otros usos de este término, véase César González. César González Mínguez Placa en memoria de un pregón pronunciado por César González Mínguez.Información personalNacimiento 26 de diciembre de 1943 79 añosEspaña España, PalenciaNacionalidad españolaInformación profesionalOcupación Historiador.Miembro de Institución Tello Téllez de MenesesReal Academia de la Historia [editar datos en Wikidata] César González Mínguez (Palencia, 1943) es un historia...

Argentine rugby union team, based in San Isidro Rugby teamSan Isidro (CASI)Full nameClub Atlético de San IsidroUnionURBANickname(s)Academia, Cebras,La CatedralFounded24 October 1902; 121 years ago (1902-10-24)LocationSan Isidro, Greater Buenos Aires, ArgentinaGround(s)San Isidro (Capacity: 5,000[1])PresidentPablo DevotoCoach(es)Jeronimo Rodolfo Almela UdryLeague(s)Top 1220186° 1st kit 2nd kit Official websitewww.casi.org.ar The Club Atlético de San Isidro (mostly ...

Madonna with the Blue DiademArtistRaphaelYearc. 1510-1518TypeOil on woodDimensions68 cm × 48 cm (27 in × 19 in)LocationLouvre, Paris The Madonna with the Blue Diadem is a painting by Raphael and his pupil Gianfrancesco Penni, and was most likely painted in Rome around 1510-1512, now at the Louvre. In the Louvre, the painting is named Virgin and Child with the Infant Saint John, also known as Virgin with the Veil or Virgin with the Blue Diadem.[1...

Elena Kagan (2010) Elena Kagan [ˈkeɪɡən] (* 28. April 1960 in New York City) ist eine US-amerikanische Juristin. Seit Anfang August 2010 ist sie Richterin am Obersten Gerichtshof der Vereinigten Staaten (englisch: Associate Justice of the Supreme Court of the United States). Sie ist das 112. Mitglied des Obersten Gerichts und die vierte Frau in diesem Amt. Kagan lehrte an der Juristischen Fakultät der University of Chicago, diente unter Präsident Bill Clinton als Rechtsberaterin in...

Pour les articles homonymes, voir Inigo, Mendez, Vigo et Montojo. Íñigo Méndez de Vigo Íñigo Méndez de Vigo, en 2017. Fonctions Porte-parole du gouvernement espagnol 4 novembre 2016 – 7 juin 2018(1 an, 7 mois et 3 jours) Président du gouvernement Mariano Rajoy Gouvernement Rajoy II Prédécesseur Soraya Sáenz de Santamaría Successeur Isabel Celaá Député aux Cortes Generales 13 janvier 2016 – 21 mai 2019(3 ans, 4 mois et 8 jours) Élection 20 déce...

Brett GelmanGelman di San Diego Comic-Con 2011LahirBrett Clifford Gelman6 Oktober 1976 (umur 47)Highland Park, Illinois, Amerika SerikatAlmamaterUniversity of North Carolina School of the Arts (BFA)PekerjaanAktorkomedianproduserpenulisTahun aktif2000–sekarangSuami/istriJanicza Bravo (m. 2015; c. 2018) Brett Clifford Gelman (lahir 6 Oktober 1976)[1] adalah aktor dan komedian asal Amerika Serikat.[2] Dia di kenal ka...

2015 Japanese filmFlying ColorsFilm poster advertising this film in JapanビリギャルDirected byNobuhiro DoiScreenplay byHiroshi HashimotoProduced byJun NasudaJunichi ShindōStarring Kasumi Arimura Atsushi Itō Shūhei Nomura Yūhei Ōuchida Kokoro Okuda Yō Yoshida Tetsushi Tanaka CinematographyYasushi HanamuraEdited byJunnosuke HogakiSayaka YamamotoMusic byEishi SegawaDistributed byTohoRelease date May 1, 2015 (2015-05-01) Running time117 minutesCountryJapanLanguageJapanes...

Theme park in Bottrop, Germany This article is in list format but may read better as prose. You can help by converting this article, if appropriate. Editing help is available. (February 2019)Movie Park GermanyPreviously known as Kirchhellener Märchenwald (1967–1976)Traumlandpark (1977–1985)Das Neue Traumland (1986–1991)Bavaria Filmpark Bottrop (1992–1993)Warner Bros. Movie World Germany (1996–2004)LocationBottrop, North Rhine-Westphalia, GermanyCoordinates51°37′12″N 6°58′21...

Composite material consisting of ceramic fibers in a ceramic matrix Fracture surface of a fiber-reinforced ceramic composed of SiC fibers and SiC matrix. The fiber pull-out mechanism shown is the key to CMC properties. CMC shaft sleeves In materials science ceramic matrix composites (CMCs) are a subgroup of composite materials and a subgroup of ceramics. They consist of ceramic fibers embedded in a ceramic matrix. The fibers and the matrix both can consist of any ceramic material, including c...

American English slur for poor white people, especially in the American South For other uses, see White trash (disambiguation). This poor white family from Alabama was presented in 1913 as celebrities because they had escaped the debilitating effects of hookworm disease, which, along with pellagra was endemic among poor Southern whites due to poor sanitation and the phenomenon of clay eating or dirt eating (geophagia). White trash is a derogatory racial and class-related slur[1][2...

Japanese curler Ikue KitazawaCurlerBorn (1996-10-12) October 12, 1996 (age 27)Karuizawa, NaganoTeamCurling clubKaruizawa CC, KaruizawaSkipIkue KitazawaThirdSeina NakajimaSecondMinori SuzukiLeadHasumi IshigookaAlternateAmi EnamiCurling career Member Association JapanWorld Championshipappearances2 (2019, 2022)Pacific-Asia Championshipappearances1 (2019) Medal record Women's Curling Representing Japan Pacific-Asia Championships 2019 Shenzhen Representing Nagano Japan Curling Cham...

Barbara BainBain pada 2006LahirMildred Fogel13 September 1931 (umur 92)Chicago, Illinois, Amerika SerikatAlmamaterUniversity of Illinois at Urbana-ChampaignPekerjaanPemeranpenarimodelTahun aktif1957–kiniSuami/istriMartin Landau (m. 1957; bercerai 1993)AnakSusan Landau FinchJuliet Landau Barbara Bain (nama lahir Mildred Fogel; lahir 13 September 1931) adalah seorang pemeran asal Amerika Serikat. Ia dikenal karena berperan sebagai ...

Indian motion picture company Cameo FilmsTypePrivateIndustryFilmFounded2013FoundersC. J. JayakumarHeadquartersChennai, Tamil Nadu, IndiaProductsFilm production, distribution Cameo Films is an Indian film production and distribution company based in Chennai, Tamil Nadu. It was incorporated in the year 2013 by C. J. Jayakumar. Since then, it has produced three Tamil films, Damaal Dumeel, Trisha Illana Nayanthara, Imaikkaa Nodigal and distributed Kaththi Sandai. History Cameo Films was incorpora...

Restoran Makanan India Malaysia di India Kecil, Pulau Pinang. Gaya kuliner Malaysia dipengaruhi oleh berbagai budaya dari seluruh dunia. Penduduk Malaysia terdiri terutama dari 3 etnis utama - Melayu, Tionghoa, dan India, dengan sejumlah kelompok etnis lain yang hidup bersama dalam harmoni umumnya. Sebagai hasil dari migrasi sejarah dan keuntungan geografis Malaysia, gaya kuliner Malaysia adalah campuran Melayu, Tionghoa, India, Thailand dan masakan Arab - untuk beberapa jenis. Hal ini mengak...

Great Lakes Bioenergy Research CenterGLBRC logoEstablished2007MissionTo create economically viable and environmentally sustainable biofuels and bioproductsFocusTransformative research in sustainable cropping systems, efficient biomass conversion, and field-to-product integrationDirectorTimothy J. DonohueLocationWisconsin Energy Institute, Madison, Wisconsin, United States of AmericaWebsitehttp://www.glbrc.org/ The Great Lakes Bioenergy Research Center (GLBRC) is one of four bioenergy research...

اختفاء سعيد مهران سليمان عيد تأليف محمد حلمي هلال - محمد ناصر إخراج سعيد حامد- جمال خزيم بطولة هشام سليم البلد مصر عدد الحلقات 30 مهندس الصوت مديح إبراهيم موسيقي أمير عبد المجيد منتج الشركة المصرية لمدينة الإنتاج الإعلامي السينما.كوم صفحة العمل تعديل مصدري - تعديل تد�...
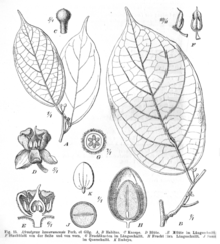
Family of flowering plants Huaceae Afrostyrax kamerunensis Scientific classification Kingdom: Plantae Clade: Tracheophytes Clade: Angiosperms Clade: Eudicots Clade: Rosids Order: Oxalidales Family: HuaceaeA.Chev.[1] This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Huaceae – news · newspapers · books · schol...

Eurymela distincta Lelompat daun adalah sejenis serangga daripada famili Cicadellidae yang merosakkan tumbuhan. Lelompat daun dapat dijumpai di seluruh dunia. Lelompat daun mempunyai kira-kira 20,000 spesies yang telah dikenalpasti. Lelompat daun (Eurymeloides bicincta: Eurymelinae) menunujkkan hubungan simbiosis dengan semut pemakan daging Pengelasan saintifik Alam: Animalia Filum: Arthropoda Kelas: Insecta Order: Hemiptera Suborder: Clypeorrhyncha Superkeluarga: Membracoidea Keluarga: Cicad...


























![{\displaystyle {\sqrt {\sqrt {1\cdot 10}}}={\sqrt[{4}]{10}}\approx 2\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7fe9ef620011045f15a3d2c3842e84fab27b4ba)
![{\displaystyle {\sqrt {\sqrt {10\cdot 100}}}={\sqrt[{4}]{1000}}\approx 6\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b0b8d8cc44d57a544d6398144d88707458ffa0)






















