Граф Хівуда
| |||||||||||||||||||||||||||||||
Read other articles:
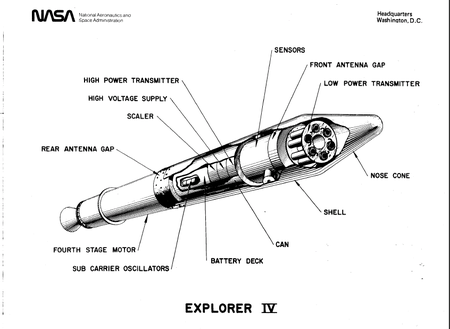
Explorer 4Explorer 4Jenis misiIlmu kebumianOperatorBadan Misil Balistik Angkatan DaratIdentifikasi Harvard1958 Epsilon 1COSPAR ID1958-005ASATCAT no.00009Durasi misi71 hari Properti wahanaProdusenJet Propulsion LaboratoryMassa luncur2.550 kilogram (5.620 pon) Awal misiTanggal luncur26 Juli 1958, 15:00:57 (26 Juli 1958, 15:00:57) UTCRoket peluncurJuno ITempat peluncuranCape Canaveral LC-5 Akhir MisiKontak terakhir5 Oktober 1958Tanggal lepas dari orbit23 Oktober 1959 Paramete...

Museo Nacional de Aeronáutica Un Gloster Meteor FMk4 en la sala central UbicaciónPaís ArgentinaLocalidad MorónDirección Av. Eva Perón 2200Coordenadas 34°40′18″S 58°38′12″O / -34.671681, -58.636792Tipo y coleccionesTipo PúblicoColecciones Aviones y elementos relacionadosHistoria y gestiónCreación 13 de enero de 1960, 63 añosPropietario Estado ArgentinoAdministrador Fuerza Aérea ArgentinaInformación para visitantesBus Desde Palermo: 166 Desde El ...

Tupolew DB-2 (ANT-37) Die ANT-37bis bei der Vorbereitung zum Rekordflug am 24. September 1938 Typ Bomber Entwurfsland Sowjetunion 1923 Sowjetunion Hersteller Tupolew / ZAGI Erstflug 16. Juli 1935 Stückzahl 3 Die Tupolew DB-2 (russisch Туполев ДБ-2, Werksbezeichnung ANT-37, АНТ-37) war ein zweimotoriges sowjetisches Bombenflugzeug der 1930er Jahre, das jedoch aufgrund unbefriedigender Leistungen zugunsten der Iljuschin DB-3 nicht in den Serienbau ging. Berühmt wurde der Typ ...

Henriette Louise de Bourbon-CondéFonctionAbbesseAbbaye de Beaumont1733-1772BiographieNaissance 14 janvier 1703Château de VersaillesDécès 19 septembre 1772 (à 69 ans)Beaumont-lès-ToursActivité ReligieuseFamille Maison de Bourbon-CondéPère Louis III de Bourbon-CondéMère Louise Françoise de BourbonFratrie Marie Gabrielle Éléonore de BourbonLouis IV Henri de Bourbon-CondéLouise-Élisabeth de Bourbon-CondéLouise Anne de BourbonMarie Anne de Bourbon-CondéCharles de B...

2023年 3月(弥生) 日 月 火 水 木 金 土 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 365日 各月 1 2 3 4 5 6 7 8 9 10 11 12 3月18日(さんがつじゅうはちにち)は、グレゴリオ暦で年始から77日目(閏年では78日目)にあたり、年末まであと288日ある。 できごと ポーランド・ソビエト・リガ平和条約(1921)。画像はベラルーシの分割を批判する風刺画。 先代の首相...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) 15 يوليو 1945. ناجون من معسكر بوخنفالد يصلون إلى حيفا وقبض عليهم البريطانيون فيما بعد.كانت هذه المقالة جزء م�...

Indian actor Saiju KurupBorn (1979-03-12) 12 March 1979 (age 44)Panavally, Kerala, IndiaNationalityIndianOccupationActorYears active2005–presentSpouse Anupama Nambiar (m. 2005)Children2ParentsN. Govinda KurupSobhana Kurup Saiju Kurup (born 12 March 1979) is an Indian actor who works predominantly in Malayalam cinema and occasionally in Tamil cinema. He is credited as Anirudh in Tamil movies. He debuted in Mayookham (2005) by Hariharan. As of June 202...

Genus of gastropods Margarella Shell of Margarella antarctica (syntype at MNHN, Paris) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Mollusca Class: Gastropoda Subclass: Vetigastropoda Order: Trochida Superfamily: Trochoidea Family: Calliostomatidae Genus: MargarellaThiele, 1893[1] Type species Margarella expansa G.B. Sowerby I, 1838 Synonyms[2] Margaritella Thiele, 1891 (Invalid: junior homonym of Margaritella Meek & Hayden, 1860; Margarella is a r...

American actor Paul JenkinsJenkins as Tom Jenkins in The Secrets of Isis, 1975Born(1938-08-02)August 2, 1938Philadelphia, PennsylvaniaDiedJuly 1, 2013(2013-07-01) (aged 74)OccupationActorYears active1968–2005Known forThe WaltonsDynastySpouseSally Kemp Paul R. Jenkins (August 2, 1938 – July 1, 2013) was an American actor. He appeared in films such as Network and Chinatown, and also single appearances in television shows such as M*A*S*H, Columbo, Lou Grant, Kojak, The Partrid...

History of Myanmar Prehistory of Myanmar 11,000–200 BCE Pyu city-states 200 BCE – 1050 CE (Sri Ksetra Kingdom, Tagaung Kingdom) Mon kingdoms 825?–1057? CE (Thaton Kingdom) Arakanese kingdoms 788?–1406 Pagan Kingdom 849–1297 Early Pagan Kingdom 849–1044 Warring states period Upper Myanmar 1297–1555 Myinsaing and Pinya Kingdoms 1297–1365 Sagaing Kingdom 1315–1365 Kingdom of Ava 1365–1555 Prome Kingdom 1482–1542 Hanthawaddy Kingdom 1287–1539, 1550–1552 Shan States 1215�...

Escudo de la policía franquista Policía franquista es un término genérico empleado por la historiografía[1][2] y los medios de comunicación[3][4] para referirse a las fuerzas de policía que existieron en España durante la Dictadura franquista (1939-1975) y, en ocasiones, también durante los primeros años de la Transición. Historia En 1939, incluso antes del final de la Guerra Civil Española con la victoria del bando sublevado, las fuerzas de orden públ...

Die Dreikönigskirche, Blick von der Königstraße Die Dresdner Dreikönigskirche ist ein Sakralbau in der Inneren Neustadt. Sie ist Zentrum einer Kirchengemeinde und wird auch unter dem Namen Haus der Kirche als Veranstaltungsort genutzt. Erstmals erwähnt wurde ein Kirchenbauwerk an dem Standort im frühen 15. Jahrhundert. Nach ihrer weitgehenden Zerstörung im Zweiten Weltkrieg wurde die Dreikönigskirche erst in den späten 1980er-Jahren wiedererrichtet, finanziert aus einem Kirchenb...

Into the Unknown Cover of the first editionAuthorsLogan Bonner, Matt Sernett, and Jeff MorgenrothCountryUnited StatesLanguageEnglishSubjectRole-playing gamesGenreDungeons & DragonsPublisherWizards of the CoastPublication date2012Media typePrint (Trade hardcover) Into the Unknown: The Dungeon Survival Handbook is a supplement for the 4th edition of the Dungeons & Dragons fantasy role-playing game. Contents Into the Unknown contains an assortment of new powers, equipment, feats, ch...

1992 studio album by Vanessa Paradis Vanessa ParadisStudio album by Vanessa ParadisReleased21 September 1992Recorded1992StudioWaterfront (Hoboken, New Jersey)LabelRemarkProducerLenny KravitzVanessa Paradis chronology Variations sur le même t'aime(1990) Vanessa Paradis(1992) Live(1994) Singles from Vanessa Paradis Be My BabyReleased: September 1992 Sunday MondaysReleased: January 1993 Natural HighReleased: May 1993 Just as Long as You Are ThereReleased: July 1993 Vanessa Paradis is the th...

The Bus is a reality television show created by Endemol, in which a group of people live together in a large and luxury bus, isolated from the outside world but continuously watched by television cameras. Each series lasts for around three months. The contestants try to win a cash prize by avoiding periodic evictions from the bus. The first The Bus broadcast was in the Netherlands in 2000 on the SBS 6 TV channel. The Bus around the world Country Local title Network Winners Main presenters Ben...
The King's Avatar (web series) redirects here. For the animated series, see The King's Avatar (2017 web series). Chinese TV series or program The King's AvatarGenreEsportsYouthBased onQuan Zhi Gao Shou by Hu DielanWritten byQiao BingqingYu YanZhou SenBao XiangZhao ZhonghaoLi Zhen[1]Directed byShi YiyueStarring Yang Yang Jiang Shuying Opening themeLight From The Ashes by Cai WeizeEnding themeGlory Battlefield by R1SEComposerRoc ChenCountry of originChinaOriginal languageMandarinNo...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Micro Dynamic Rifle eXtreme A Compliant Desert Tech MDRx Rifle with 3-15 Scope, Bipod, front QD, Ratchet Compensator, Saddle Blanket, Front and Rear backup sights, over molded hand guard, and Trigger Lock Jenis BullpupSemi-automatic rifleAssault rifle...

Nonprofit, professional organization representing organized dentistry in California This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (June 2019) (Learn how and when to remove this template message) California Dental AssociationFormation1870TypeProfessional associationHe...

2018 Tower Hamlets Council election ← 2014 3 May 2018 2022 → All 45 seats to Tower Hamlets London Borough Council23 seats needed for a majority First party Second party Third party Party Labour Conservative PATH Last election 22 seats, 38.6% 5 seats, 12.1% Did not stand Seats before 22 5 6 Seats won 42 2 1 Seat change 20 3 5 Popular vote 79,551 17,107 19,580 Percentage 46.1% 9.9% 11.3% Swing 7.5% 2.2% New Fourth party Fifth ...

Para otros usos de este término, véase Rana (desambiguación). No debe confundirse con Sapo. Ranidae Rana verde (Rana clamitans)TaxonomíaReino: AnimaliaFilo: ChordataClase: AmphibiaOrden: AnuraFamilia: RanidaeRafinesque, 1814Géneros Véase el texto [editar datos en Wikidata] Los ránidos (Ranidae) son una familia de anfibios anuros, conocidos vulgarmente como ranas, aunque muchas otras especies de otras familias reciben también este nombre popular; así, los ránidos so...





![Багатогранник Сілаші[ru].](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Szilassi_polyhedron.svg/120px-Szilassi_polyhedron.svg.png)



![Вкладення графу Хівуда в тор(показаний у вигляді квадрата з Періодичними граничними умовами[en]), розділяє його на сім взаємно-суміжних областей](http://upload.wikimedia.org/wikipedia/commons/thumb/c/c4/7x-torus.svg/120px-7x-torus.svg.png)
