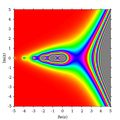
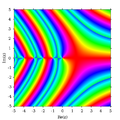
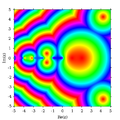
ฟังก์ชันแกมมา
|
Read other articles:

In this Ottoman Turkish style name, the given name is Osman Bayezid. There is no family name. Head of the Osmanoğlu family Bayezid Osman OsmanoğluHead of the Osmanoğlu familyTerm23 September 2009 – 6 January 2017PredecessorŞehzade Ertuğrul OsmanSuccessorŞehzade Dündar Ali OsmanBorn(1924-06-23)23 June 1924Paris, FranceDied6 January 2017(2017-01-06) (aged 92)New York City, United StatesHouseImperial House of OsmanFatherŞehzade Ibrahim TevfikMotherHatice Şadiye Hanım Bayezid Osm...

لمعانٍ أخرى، طالع أكبر أباد (توضيح). أكبر أباد تقسيم إداري البلد إيران إحداثيات 32°25′32″N 51°36′46″E / 32.4256°N 51.6128°E / 32.4256; 51.6128 السكان التعداد السكاني 252 نسمة (إحصاء 2016) تعديل مصدري - تعديل أكبر أباد هي قرية في مقاطعة مباركة، إيران.[1] يقدر عدد سكانه...

Anang SyakhfianiBupati Tabalong ke-9Masa jabatan2014 – petahanaWakilZony Alfianoor MawardiPendahuluRachman RamsyiPenggantimasih menjabat Informasi pribadiLahir26 Juni 1960 (umur 63)Murung Pudak, Kalimantan SelatanKebangsaanIndonesiaPartai politik PANSunting kotak info • L • B Drs. H. Anang Syakhfiani, M.Si. (lahir 26 Juni 1960) adalah bupati Tabalong yang menjabat saat ini untuk masa periode 2014–2019.[1] Ia menjabat sebagai bupati Tabalo...

Igor Belanov Informasi pribadiNama lengkap Igor Ivanovich BelanovTanggal lahir 25 September 1960 (umur 63)Tempat lahir Odessa, Ukraina SSR, Uni SovietTinggi 1,74 m (5 ft 8+1⁄2 in)Posisi bermain Gelandang penyerangKarier junior1973–1978 Chornomorets OdessaKarier senior*Tahun Tim Tampil (Gol)1979–1980 SKA Odessa 68 (16)1981–1984 Chornomorets Odessa 116 (26)1985–1989 Dynamo Kyiv 121 (39)1989–1990 Borussia M'gladbach 24 (4)1991–1995 Eintracht Braunschweig 67 ...

Regering-Theunis IV Regeringsleider Georges Theunis Coalitie Katholieke Unie Liberale Partij Zetels Kamer 104 van 187 (27 november 1932) Premier Georges Theunis Aantreden 20 november 1934 Ontslagnemend 19 maart 1935 Einddatum 25 maart 1935 Voorganger De Broqueville V Opvolger Van Zeeland I Portaal België De regering-Theunis IV (20 november 1934 - 25 maart 1935) was een Belgische regering. Het was een coalitie tussen de Katholieke Unie (80 zetels) en de Liberale P...

عبد الله محمد علي نعمة معلومات شخصية تاريخ الميلاد سنة 1916 تاريخ الوفاة 1994 الحياة العملية المهنة كاتب تعديل مصدري - تعديل العلامة القاضي الشيخ عبدالله نعمة عالم وشاعر وأديب ورئيس المحاكم الجعفرية في لبنان. نسبه هو الشيخ عبد الله بن الشيخ محمد علي نعمة بن الشيخ يحيى

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Institut Teknologi Termal Moskwa – berita · surat kabar · buku · cendekiawan · JSTOR Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambah...

Church in New Jersey , United StatesStony Brook MeetinghouseThe meetinghouse in 1936 from the Historic American Buildings SurveyLocation470 Quaker Rd, Princeton, New Jersey 08540Country United StatesDenominationQuakerHistoryFounded1726Princeton Battlefield / Stony Brook Village Historic DistrictU.S. National Register of Historic PlacesU.S. Historic districtContributing property Show map of Mercer County, New JerseyShow map of New JerseyShow map of the United StatesCoordinates40°19′36.8

Ішхі-АддуНародився 2 тисячоліття до н. е.Помер 18 століття до н. е.Діти Амут-пі'ел II Ішхі-Адду (1-а пол. XVIII ст. до н. е.) — цар держави Катна. За його панування вона досягла найбільшого піднесення, перетворившись на значну потугу в Передній Азії. Життєпис Походив з Аморейс

Halaman ini berisi artikel tentang pulau legenda. Untuk tempat tinggal Mukesh Ambani, lihat Antilia (bangunan). Untuk genus tumbuhan, lihat Antillia (tumbuhan). Untuk kota Italia, lihat Montano Antilia. AntilliaPeta Albino de Canepa, 1489. Pulau fantom Antillia, dengan Tujuh Kota-nya, di bagian kanan; pulau kecil Roilloberada di bagian kirinya.TipePulau hantu Antillia (atau Antilia) adalah sebuah pulau hantu, pada zaman penjelajahan abad ke-15, yang berada di Samudra Atlantik, yang berada jau...

Short story by Ray Bradbury The Toynbee ConvectorShort story by Ray BradburyCover of a reprint of The Toynbee Convector, which collects the storyCountryUnited StatesLanguageEnglishGenre(s)science fictionPublicationPublished inPlayboyPublication typePeriodicalMedia typePrint (Magazine)Publication dateJanuary 1984 The Toynbee Convector is a science fiction short story by American writer Ray Bradbury. First published in Playboy magazine in 1984,[1] the story was subsequently featured in ...

Two French girls sentenced for a February 1933 murder This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Christine and Léa Papin – news · newspapers · books · scholar · JSTOR (September 2022) (Learn how and when to remove this template message) Léa (left) and Christine Papin Christine Papin (8 March 1905 – ...

The topic of this article may not meet Wikipedia's notability guideline for music. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted.Find sources: Dedicated Barry White album – news · newspapers · books · scholar · ...

Pakistani actress (born 1984) Mahira KhanKhan in 2018BornMahira Hafeez Khan (1984-12-21) 21 December 1984 (age 38)Karachi, Sindh, PakistanAlma materFoundation Public SchoolOccupationActressYears active2006–presentSpouses Ali Askari (m. 2007; div. 2015) Salim Karim (m. 2023) Children1AwardsFull list Mahira Hafeez Khan (pronounced [maɦiːra hafiːz xaːn] born 21 December 1984) is a Paki...

الاتحاد العام للكتاب والأدباء الفلسطينيين البلد دولة فلسطين تاريخ التأسيس 1966 منطقة الخدمة فلسطين والخارج اللغات الرسمية عربية المنظمة الأم منظمة التحرير الفلسطينية الموقع الرسمي الموقع الرسمي تعديل مصدري - تعديل الاتحاد العام للكتاب والأدباء الفلسطيني...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Bumi Serpong Damai – berita · surat kabar · buku · cendekiawan · JSTOR Untuk pengembang kawasan ini, lihat Bumi Serpong Damai (perusahaan). Untuk kegunaan lain, lihat BSD. Bumi Serpong DamaiNama lainBSD ...

Корпус дросельної заслінки з інтегрованим електроприводом Електронне керування дросельною заслінкою (англ. Electronic throttle control, ETC) — автомобільна технологія, яка електронним способом «з'єднує» педаль акселератора з дросельною заслінкою, замінюючи механічний зв'язок. Цю...

中國國民黨第十四任總統提名選舉 ← 2016 2015年10月17日 2020 → 获提名人 朱立倫 洪秀柱 得票率 獲得徵召 廢止提名 換柱爭議,又稱換柱風波、換柱行動、棄柱行動、廢柱行動、滅柱行動,2015年在中華民國的一起政治爭議,中國國民黨廢止洪秀柱在2016年中華民國總統選舉的提名資格,改徵召另一人,造成政治爭議。 在2016年中國國民黨總統提名選舉中,洪�...

Proverbs 17← chapter 16chapter 18 →The whole Book of Proverbs in the Leningrad Codex (1008 C.E.) from an old fascimile edition.BookBook of ProverbsCategoryKetuvimChristian Bible partOld TestamentOrder in the Christian part21 Proverbs 17 is the seventeenth chapter of the Book of Proverbs in the Hebrew Bible or the Old Testament of the Christian Bible.[1][2] The book is a compilation of several wisdom literature collections, with the heading in 1:1 may be intended ...

Woodworking shaping and finishing tool For the metalworking handtool, see Hand scraper. This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Card scraper – news · newspapers · books · scholar · JSTOR (April 2020) Card scraper in use A card scraper or cabinet scraper is a woodworking shaping and finishin...