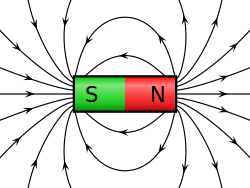
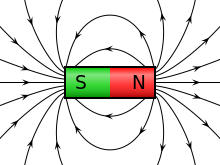
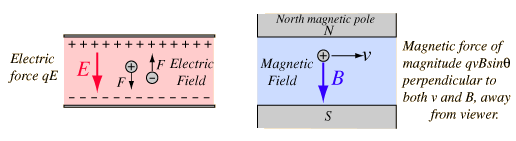
అయస్కాంత క్షేత్రం
|
Read other articles:
Adolfo Teodoro Álvarez Miembro de la Junta Revolucionaria 28-29 de junio de 1966Junto con Pascual Pistarini y Benigno VarelaPredecesor cargo creadoSucesor cargo disuelto Comandante en Jefe de la Fuerza Aérea Argentina 27 de mayo de 1966-29 de agosto de 1968Predecesor Carlos Segundo Conrado ArmaniniSucesor Jorge Miguel Martínez Zuviría Secretario de Estado de Aeronáutica de la Nación Argentina 30 de junio-1 de septiembre de 1966Predecesor Mario RomanelliSucesor él mismo como comandante ...

Computer software environment with own programming language SpeakeasyDeveloper(s)Speakeasy Computing CorporationStable releaseIV Iota / 2006 Written inMortran, FORTRAN, C[citation needed]Operating systemWindows, macOS, RedHat Linux, SUSE Linux, Mandrake Linux, Debian, Solaris, HP-UX[1]TypeTechnical computingLicenseTrialware Speakeasy (the interpreted programming language)ParadigmimperativeDesigned byStanley CohenDeveloperSpeakeasy Computing CorporationFirst appeared1...

Ге́рб Ме́ди ДеталіНосій МедаЗатверджений 8 листопада 1935Корона міськаЩит португальськийДевіз vila de MêdaВикористання територіальний Ге́рб Ме́ди — офіційний символ міста Меда, Португалія. Використовується як територіальний герб. У срібному щиті зелена копиця (порт. mêda) пш�...

Depuis la construction du siège de la Turkish Petroleum en 1974, 110 gratte-ciel (immeuble de 100 mètres de hauteur et plus) ont été construits à Ankara dans la capitale de la Turquie. En octobre 2018 la liste des immeubles d'au minimum 110 mètres de hauteur est la suivante d'après Emporis et le CTBUH [1],[2] TOBB Towers Sheraton Hotel Ankara Dikmen Valley Towers Halkbank Headquarters Cankaya Hotel Rang Nom Hauteur Étages Année 1 Elya Royal Tower 195 m [3] 45 2020 2 T�...

Карл Отто Густав ВехтерKarl Otto Gustav Wächter Карл Отто Густав Вехтер 2-й губернатор Дистрикту Галичина 1942 — 1944 Попередник: Карл фон Ляш Наступник: немає Народження: 8 липня 1901(1901-07-08)Відень Смерть: 1 серпня 1949(1949-08-01) (48 років)Рим Причина смерті: лептоспіроз Поховання: Кампо В

The Tomboy, lukisan tahun 1873 karya John George Brown Tomboi atau tomboy (bahasa Inggris: Tomboy) adalah seorang perempuan yang memiliki sifat atau perilaku yang dianggap oleh masyarakat sebagai peran gender laki-laki,[1][2] seperti mengenakan pakaian maskulin atau bermain permainan yang dianggap sebagai permainan laki-laki.[2] Istilah tomboi berasal dari bahasa Inggris, dan menurut Oxford English Dictionary terkait dengan konotasi kekasaran dan ketidakpantasan.&#...

Confederacy Treasury Dept coverVarious departments of the Confederate government used envelopes which were printed with the names of their department. Examples where the words 'Official Business' occurs are common. The postage stamps and postal system of the Confederate States of America carried the mail of the Confederacy for a brief period in American history. Early in 1861 when South Carolina no longer considered itself part of the Union and demanded that the U.S. Army abandon Fort Sumter,...

Japanese actress Kana Asumi阿澄 佳奈Kana Asumi in 2021Born (1983-08-12) August 12, 1983 (age 40)[1][2][3]Fukuoka Prefecture, JapanOccupations Actress voice actress singer Years active1999–presentAgent81 ProduceNotable work Honkai Impact 3rd as Bronya Zaychik Non Non Biyori as Komari Koshigaya Encouragement of Climb as Hinata Kuraue Working!! as Popura Taneshima Nyaruko: Crawling with Love as Nyaruko Blue Archive as Kuda Izuna Honkai: Star Rail as Bronya...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2022) خورخي مارسيلو رودريغيز معلومات شخصية الميلاد 13 يناير 1985 (العمر 38 سنة)مونتفيدو الطول 1.73 م (5 قدم 8 بوصة) مركز اللعب وسط الجنسية الأوروغواي مع...

Surah ke-59al-Hasyr PengusiranTeks ArabTerjemahan KemenagKlasifikasiMadaniyahJuzJuz 28Jumlah ruku3 ruku'Jumlah ayat24 ayat Surah Al-Hasyr (Arab: الحشر, Pengusiran) adalah surah ke-59 dalam al-Qur'an. Surah ini tergolong surah Madaniyah yang terdiri atas 24 ayat. Dinamakan Al Hasyr yang berarti pengusiran diambil dari perkataan Al Hasyr yang terdapat pada ayat ke-2 surat ini. Di dalam surat ini disebutkan kisah pengusiran suatu suku Yahudi yang bernama Bani Nadhir yang berdiam di sekitar ...

Celtic punk band founded in London in 1982 The PoguesThe Pogues performing in 2006Background informationAlso known asPogue Mahone (1982–1984)OriginKing's Cross, London, EnglandGenresCeltic punkfolk punkYears active1982–1996, 2001–2014LabelsStiffIslandPogue MahoneChameleonPast members Shane MacGowan Spider Stacy Jem Finer Darryl Hunt Andrew Ranken James Fearnley Terry Woods Cait O'Riordan Philip Chevron Joe Strummer Dave Coulter James McNally Jamie Clarke Websitepogues.com The Pogues wer...

1918 film The Forbidden PathNewspaper advertisement.Directed byJ. Gordon EdwardsWritten byAdrian Johnson (scenario)Screenplay byE. Lloyd SheldonStory byE. Lloyd SheldonProduced byWilliam FoxStarringTheda BaraHugh ThompsonCinematographyJohn W. BoyleDistributed byFox Film CorporationRelease date February 3, 1918 (1918-02-03) Running time6 reelsCountryUnited StatesLanguageSilent (English intertitles) The Forbidden Path is a 1918 American silent drama film directed by J. Gordon Edw...

Village in Warmian-Masurian Voivodeship, PolandTaborzecVillageTaborzecCoordinates: 54°12′N 21°21′E / 54.200°N 21.350°E / 54.200; 21.350Country PolandVoivodeshipWarmian-MasurianCountyKętrzynGminaBarciany Taborzec [taˈbɔʐɛt͡s] is a village in the administrative district of Gmina Barciany, within Kętrzyn County, Warmian-Masurian Voivodeship, in northern Poland, close to the border with the Kaliningrad Oblast of Russia.[1] It lies approximately 2 kil...

Boundary of New Territories East constituency from 1998 to 2021, also the mostly-recognised boundary of the region New Territories East is the eastern part of New Territories, covering North, Tai Po, Sha Tin, and Sai Kung District. History All districts except Sai Kung District have been connected by the Kowloon–Canton Railway (now East Rail line) since its completion in 1910, and later the Tai Po Road. In 1985, East New Territories and South New Territories electoral-college constituencies...

1999 live album by Jaki ByardJuly in ParisLive album by Jaki ByardReleased1999RecordedJuly 24–25, 1998GenreJazzLabelFairplay Professional ratingsReview scoresSourceRatingAllMusic[1] July in Paris is an album by pianist Jaki Byard. Most of the tracks are trio, with bassist Ralph Hamperian, and drummer Richard Allen; on two they are joined by saxophonist Ricky Ford. Recording and music The album was recorded in concert on July 24 and July 25, 1998.[1] The tracks are di...

1997 Slovenian filmOutsiderFilm posterDirected byAndrej KošakWritten byAndrej KošakStarringDemeter BitencMiranda CaharijaNina IvaničJure IvanušičDavor JanjićUroš PotočnikZijah SokolovićCinematographySven PepeonikEdited byZlatjan ČučkovMusic bySaša LošićDistributed byRTV SlovenijaBindweed SoundvisionRelease date 1997 (1997) Running time100 minutesCountrySloveniaLanguageSlovene Outsider is a film produced in 1997 in Slovenia by writer and director Andrej Košak. The film was ...

Different types of public transport in Mumbai A traffic intersection in Mumbai, 2009 Map, railway lines, ports and airports (Click to enlarge) Transport in Mumbai is achieved by both public, and private transport. As of 2015, 52% of commuters use public transport.[1] Mumbai has the largest organized bus transport network among major Indian cities. Mumbai's public transport consists primarily of rapid transit on exclusive suburban railway lines augmented by commuter rail on main lines ...

Place in Lower Carniola, SloveniaZavinekZavinekLocation in SloveniaCoordinates: 45°54′11.96″N 15°17′59.65″E / 45.9033222°N 15.2999028°E / 45.9033222; 15.2999028Country SloveniaTraditional regionLower CarniolaStatistical regionSoutheast SloveniaMunicipalityŠkocjanArea • Total0.86 km2 (0.33 sq mi)Elevation180.1 m (590.9 ft)Population (2002) • Total62[1] Zavinek (pronounced [zaˈʋiːnək];...

German politician (1865–1939) Philipp ScheidemannMinister President of GermanyIn office13 February 1919 – 20 June 1919PresidentFriedrich EbertDeputyEugen SchifferBernhard DernburgPreceded byFriedrich Ebert (de facto)Succeeded byGustav BauerMayor of KasselIn office19 November 1919 – 1 October 1925Preceded byErich Koch-WeserSucceeded byHerbert StadlerMinister for the ColoniesIn office13 December 1918 – 13 February 1919ChancellorFriedrich EbertPreceded byWilhel...

Lacanau La Canau Entidad subnacional Escudo Lacanau La CanauLocalización de Lacanau La Canau en Francia Coordenadas 44°58′45″N 1°04′46″O / 44.979166666667, -1.0794444444444Entidad Comuna de Francia • País Francia • Región Nueva Aquitania • Departamento Gironda • Distrito Distrito de Burdeos • Cantón Castelnau-de-Médoc • Mancomunidad Communauté de communes des Lacs MédocainsAlcalde Jean-Michel David(2001-200...