–§–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞
–°—Г–Љ–Љ–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е –љ–µ—З—С—В–љ—Л—Е —З–Є—Б–µ–ї –µ—Б—В—М –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ –§–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞ вАФ —З–Є—Б–ї–∞, –Ї–Њ—В–Њ—А—Л–µ –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М —Б –њ–Њ–Љ–Њ—Й—М—О –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е —Д–Є–≥—Г—А. –≠—В–Њ –Є—Б—В–Њ—А–Є—З–µ—Б–Ї–Њ–µ –њ–Њ–љ—П—В–Є–µ –≤–Њ—Б—Е–Њ–і–Є—В –Ї –њ–Є—Д–∞–≥–Њ—А–µ–є—Ж–∞–Љ , –Ї–Њ—В–Њ—А—Л–µ —А–∞–Ј–≤–Є–≤–∞–ї–Є –∞–ї–≥–µ–±—А—Г –љ–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є –Њ—Б–љ–Њ–≤–µ –Є –њ—А–µ–і—Б—В–∞–≤–ї—П–ї–Є –ї—О–±–Њ–µ –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ–µ —Ж–µ–ї–Њ–µ —З–Є—Б–ї–Њ –≤ –≤–Є–і–µ –љ–∞–±–Њ—А–∞ —В–Њ—З–µ–Ї –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є[ 1] ¬Ђ–≤–Њ–Ј–≤–µ—Б—В–Є —З–Є—Б–ї–Њ –≤ –Ї–≤–∞–і—А–∞—В¬ї –Є–ї–Є ¬Ђ–≤ –Ї—Г–±¬ї [ 2]
–Ґ—А–∞–і–Є—Ж–Є–Њ–љ–љ–Њ —А–∞–Ј–ї–Є—З–∞—О—В –і–≤–∞ –Њ—Б–љ–Њ–≤–љ—Л—Е –Ї–ї–∞—Б—Б–∞ —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї[ 3]
–њ–ї–Њ—Б–Ї–Є–µ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ вАФ —З–Є—Б–ї–∞, —Б–≤—П–Ј–∞–љ–љ—Л–µ —Б –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л–Љ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ. –Ю–љ–Є –і–µ–ї—П—В—Б—П –љ–∞ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–µвЮ§ вЮ§ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Л–µ –Љ–љ–Њ–≥–Њ–≥—А–∞–љ–љ—Л–µ —З–Є—Б–ї–∞ вАФ —З–Є—Б–ї–∞, —Б–≤—П–Ј–∞–љ–љ—Л–µ —Б –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л–Љ –Љ–љ–Њ–≥–Њ–≥—А–∞–љ–љ–Є–Ї–Њ–ЉвЮ§ –Т —Б–≤–Њ—О –Њ—З–µ—А–µ–і—М, –Ї–∞–ґ–і—Л–є –Ї–ї–∞—Б—Б —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї –і–µ–ї–Є—В—Б—П –љ–∞ —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–Є , –Ї–∞–ґ–і–∞—П –Є–Ј –Ї–Њ—В–Њ—А—Л—Е —Б–≤—П–Ј–∞–љ–∞ —Б –Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ–є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Д–Є–≥—Г—А–Њ–є: —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ, –Ї–≤–∞–і—А–∞—В–Њ–Љ, —В–µ—В—А–∞—Н–і—А–Њ–Љ –Є —В. –і.
–°—Г—Й–µ—Б—В–≤—Г—О—В —В–∞–Ї–ґ–µ –Њ–±–Њ–±—Й–µ–љ–Є—П —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї –љ–∞ –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞вЮ§ вЮ§
–Т —В–µ–Њ—А–Є–Є —З–Є—Б–µ–ї –Є –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–µ —Д–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞ —Б–≤—П–Ј–∞–љ—Л —Б –Љ–љ–Њ–≥–Є–Љ–Є –і—А—Г–≥–Є–Љ–Є –Ї–ї–∞—Б—Б–∞–Љ–Є —Ж–µ–ї—Л—Е —З–Є—Б–µ–ї вЮ§ –±–Є–љ–Њ–Љ–Є–∞–ї—М–љ—Л–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є , —Б–Њ–≤–µ—А—И–µ–љ–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є , —З–Є—Б–ї–∞–Љ–Є –Ь–µ—А—Б–µ–љ–љ–∞ , –§–µ—А–Љ–∞ , –§–Є–±–Њ–љ–∞—З—З–Є , –Ы—О–Ї–∞ –Є –і—А—Г–≥–Є–Љ–Є[ 4]
–Ф–ї—П –Ї—А–∞—В–Ї–Њ—Б—В–Є –≤ —Н—В–Њ–Љ —А–∞–Ј–і–µ–ї–µ –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–µ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –љ–∞–Ј—Л–≤–∞—О—В—Б—П –њ—А–Њ—Б—В–Њ ¬Ђ–Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є¬ї.
–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –њ–Њ—Б—В—А–Њ–µ–љ–Є–µ —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Ь–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ вАФ —Н—В–Њ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М, —Г–Ї–∞–Ј—Л–≤–∞—О—Й–∞—П —З–Є—Б–ї–Њ —В–Њ—З–µ–Ї, –њ–Њ—Б—В—А–Њ–µ–љ–љ—Г—О —Б–Њ–≥–ї–∞—Б–љ–Њ –њ—А–∞–≤–Є–ї–∞–Љ, –Ї–Њ—В–Њ—А—Л–µ –њ—А–Њ–Є–ї–ї—О—Б—В—А–Є—А—Г–µ–Љ –љ–∞ –њ—А–Є–Љ–µ—А–µ —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї–∞. –†—П–і —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –љ–∞—З–Є–љ–∞–µ—В—Б—П —Б 1 (–±–∞–Ј–Њ–≤–∞—П —В–Њ—З–Ї–∞), –Ј–∞—В–µ–Љ —Б–ї–µ–і—Г–µ—В 7, –њ–Њ—В–Њ–Љ—Г —З—В–Њ 7 —В–Њ—З–µ–Ї –Њ–±—А–∞–Ј—Г—О—В –њ—А–∞–≤–Є–ї—М–љ—Л–є —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї , 6 —В–Њ—З–µ–Ї –і–Њ–±–∞–≤–Є–ї–Є—Б—М. –Ґ—А–µ—В—М–µ —З–Є—Б–ї–Њ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї—Г, —Г –Ї–Њ—В–Њ—А–Њ–≥–Њ —Б—В–Њ—А–Њ–љ—Л —Б–Њ–і–µ—А–ґ–∞—В —Г–ґ–µ –љ–µ –њ–Њ –і–≤–µ, –∞ –њ–Њ —В—А–Є —В–Њ—З–Ї–Є, –њ—А–Є—З—С–Љ –≤—Б–µ —В–Њ—З–Ї–Є, –њ–Њ—Б—В—А–Њ–µ–љ–љ—Л–µ –љ–∞ –њ—А–µ–і—Л–і—Г—Й–Є—Е —И–∞–≥–∞—Е, —В–∞–Ї–ґ–µ —Г—З–Є—В—Л–≤–∞—О—В—Б—П. –Ш–Ј —А–Є—Б—Г–љ–Ї–∞ –≤–Є–і–љ–Њ, —З—В–Њ —В—А–µ—В—М—П —Д–Є–≥—Г—А–∞ —Б–Њ–і–µ—А–ґ–Є—В 18 —В–Њ—З–µ–Ї, –њ—А–Є–±–∞–≤–Ї–∞ (–Я–Є—Д–∞–≥–Њ—А –љ–∞–Ј—Л–≤–∞–ї –µ—С ¬Ђ–≥–љ–Њ–Љ–Њ–љ –∞—А–Є—Д–Љ–µ—В–Є—З–µ—Б–Ї—Г—О –њ—А–Њ–≥—А–µ—Б—Б–Є—О , –≤ –Ї–Њ—В–Њ—А–Њ–є –Ї–∞–ґ–і—Л–є —З–ї–µ–љ –љ–∞ 5 –±–Њ–ї—М—И–µ, —З–µ–Љ –њ—А–µ–і—Л–і—Г—Й–Є–є[ 5]
–Я–µ—А–µ—Е–Њ–і—П –Ї –Њ–±—Й–µ–Љ—Г
k
{\displaystyle k}
[ 5]
k
− вИТ -->
2.
{\displaystyle k-2.}
–Ю–±—Й–µ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ k -—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞ –і–ї—П –ї—О–±–Њ–≥–Њ
k
⩾ в©Њ -->
3
{\displaystyle k\geqslant 3}
[ 6]
–Э–∞–њ—А–Є–Љ–µ—А, —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –њ–Њ–ї—Г—З–∞—О—В—Б—П –Ї–∞–Ї —З–∞—Б—В–Є—З–љ—Л–µ —Б—Г–Љ–Љ—Л —А—П–і–∞
1
+
2
+
3
+
4
… вА¶ -->
{\displaystyle 1+2+3+4\dots }
1
+
3
+
5
+
7
… вА¶ -->
{\displaystyle 1+3+5+7\dots }
–Я–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М k -—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Є–Љ–µ–µ—В –≤–Є–і[ 7]
1
,
k
,
3
k
− вИТ -->
3
,
6
k
− вИТ -->
8
,
10
k
− вИТ -->
15
,
15
k
− вИТ -->
24
,
21
k
− вИТ -->
35
,
28
k
− вИТ -->
48
,
36
k
− вИТ -->
63
,
45
k
− вИТ -->
80
… вА¶ -->
{\displaystyle 1,\;k,\;3k-3,\;6k-8,\;10k-15,\;15k-24,\;21k-35,\;28k-48,\;36k-63,\;45k-80\dots }
–Ю–±—Й—Г—О —Д–Њ—А–Љ—Г–ї—Г –і–ї—П —П–≤–љ–Њ–≥–Њ –њ–Њ–і—Б—З—С—В–∞
n
{\displaystyle n}
k -—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
[ 8]
P
n
(
k
)
=
n
+
(
k
− вИТ -->
2
)
n
(
n
− вИТ -->
1
)
2
=
(
k
− вИТ -->
2
)
n
2
− вИТ -->
(
k
− вИТ -->
4
)
n
2
=
1
2
k
(
n
2
− вИТ -->
n
)
− вИТ -->
n
2
+
2
n
{\textstyle P_{n}^{(k)}=n+(k-2){\frac {n(n-1)}{2}}={\frac {(k-2)n^{2}-(k-4)n}{2}}={\frac {1}{2}}k(n^{2}-n)-n^{2}+2n}
(–Ю–Ъ–§)
–Т –љ–µ–Ї–Њ—В–Њ—А—Л—Е –Є—Б—В–Њ—З–љ–Є–Ї–∞—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї –љ–∞—З–Є–љ–∞—О—В —Б –љ—Г–ї—П (–љ–∞–њ—А–Є–Љ–µ—А, –≤ A000217 ):
0
,
1
,
k
,
3
k
− вИТ -->
3
,
… вА¶ -->
{\displaystyle 0,\;1,\;k,\;3k-3,\dots }
–Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –≤ –Њ–±—Й–µ–є —Д–Њ—А–Љ—Г–ї–µ –і–ї—П
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
n
=
0.
{\displaystyle n=0.}
—А–∞—Б—И–Є—А–µ–љ–љ—Л–є —А—П–і –Њ–≥–Њ–≤–∞—А–Є–≤–∞–µ—В—Б—П –Њ—Б–Њ–±–Њ.
–°—Г—Й–µ—Б—В–≤—Г–µ—В —В–∞–Ї–ґ–µ —А–µ–Ї—Г—А—А–µ–љ—В–љ–∞—П —Д–Њ—А–Љ—Г–ї–∞ –і–ї—П –≤—Л—З–Є—Б–ї–µ–љ–Є—П –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞[ 8]
P
n
(
k
)
=
{
1
,
n
=
1
P
n
− вИТ -->
1
(
k
)
+
(
k
− вИТ -->
2
)
(
n
− вИТ -->
1
)
+
1
,
n
>
1
{\displaystyle P_{n}^{(k)}={\begin{cases}1,&n=1\\P_{n-1}^{(k)}+(k-2)(n-1)+1,&n>1\end{cases}}}
–Я—А–Є —Г–≤–µ–ї–Є—З–µ–љ–Є–Є —З–Є—Б–ї–∞ —Б—В–Њ—А–Њ–љ
k
{\displaystyle k}
–Э–Є–Ї–Њ–Љ–∞—Е–∞ [ 9]
P
n
(
k
+
1
)
=
P
n
(
k
)
+
P
n
− вИТ -->
1
(
3
)
{\displaystyle P_{n}^{(k+1)}=P_{n}^{(k)}+P_{n-1}^{(3)}}
n
>
1
{\displaystyle n>1}
(–Э–Є–Ї–Њ–Љ–∞—Е)
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
k
,
{\displaystyle k,}
P
n
(
k
+
s
)
+
P
n
(
k
− вИТ -->
s
)
=
2
P
n
(
k
)
{\displaystyle P_{n}^{(k+s)}+P_{n}^{(k-s)}=2P_{n}^{(k)}}
s
=
0
,
1
,
2
… вА¶ -->
k
− вИТ -->
3
{\displaystyle s=0,1,2\dots k-3}
–Ф—А—Г–≥–Є–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –Ї–∞–ґ–і–Њ–µ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –µ—Б—В—М —Б—А–µ–і–љ–µ–µ –∞—А–Є—Д–Љ–µ—В–Є—З–µ—Б–Ї–Њ–µ –і–ї—П —А–∞–≤–љ–Њ–Њ—В—Б—В–Њ—П—Й–Є—Е –Њ—В –љ–µ–≥–Њ –њ–Њ
k
{\displaystyle k}
–Х—Б–ї–Є
k
{\displaystyle k}
–њ—А–Њ—Б—В–Њ–µ —З–Є—Б–ї–Њ , —В–Њ –≤—В–Њ—А–Њ–µ
k
{\displaystyle k}
k
{\displaystyle k}
P
n
(
k
)
=
2
+
(
n
− вИТ -->
1
)
(
k
− вИТ -->
2
)
2
n
{\textstyle P_{n}^{(k)}={\frac {2+(n-1)(k-2)}{2}}n}
–Ф–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ: –њ—Г—Б—В—М
n
>
2.
{\displaystyle n>2.}
n
{\displaystyle n}
n
2
{\textstyle {\frac {n}{2}}}
2
+
(
n
− вИТ -->
1
)
(
k
− вИТ -->
2
)
2
{\textstyle {\frac {2+(n-1)(k-2)}{2}}}
[ 10]
–†—П–і—Л –Є–Ј –Њ–±—А–∞—В–љ—Л—Е –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї
1
P
1
(
k
)
+
1
P
2
(
k
)
+
1
P
3
(
k
)
+
⋯ вЛѓ -->
+
1
P
n
(
k
)
+
… вА¶ -->
{\displaystyle {\frac {1}{P_{1}^{(k)}}}+{\frac {1}{P_{2}^{(k)}}}+{\frac {1}{P_{3}^{(k)}}}+\dots +{\frac {1}{P_{n}^{(k)}}}+\dots }
—Б—Е–Њ–і—П—В—Б—П. –Ш—Е —Б—Г–Љ–Љ–∞
S
{\displaystyle S}
S
=
− вИТ -->
2
k
− вИТ -->
4
(
γ ќ≥ -->
+
ψ ѕИ -->
(
2
k
− вИТ -->
2
)
)
,
{\textstyle S=-{\frac {2}{k-4}}\left(\gamma +\psi ({\frac {2}{k-2}})\right),}
γ ќ≥ -->
{\displaystyle \gamma }
–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≠–є–ї–µ—А–∞ вАФ –Ь–∞—Б–Ї–µ—А–Њ–љ–Є ,
ψ ѕИ -->
(
x
)
{\displaystyle \psi (x)}
–і–Є–≥–∞–Љ–Љ–∞-—Д—Г–љ–Ї—Ж–Є—П [ 11]
–§–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞, –њ–Њ –Љ–љ–µ–љ–Є—О –њ–Є—Д–∞–≥–Њ—А–µ–є—Ж–µ–≤ , –Є–≥—А–∞—О—В –≤–∞–ґ–љ—Г—О —А–Њ–ї—М –≤ —Б—В—А—Г–Ї—В—Г—А–µ –Љ–Є—А–Њ–Ј–і–∞–љ–Є—П. –Я–Њ—Н—В–Њ–Љ—Г –Є—Е –Є–Ј—Г—З–µ–љ–Є–µ–Љ –Ј–∞–љ–Є–Љ–∞–ї–Є—Б—М –Љ–љ–Њ–≥–Є–µ –≤–Є–і–љ—Л–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –∞–љ—В–Є—З–љ–Њ—Б—В–Є: –≠—А–∞—В–Њ—Б—Д–µ–љ , –У–Є–њ—Б–Є–Ї–ї , –Ф–Є–Њ—Д–∞–љ—В –Р–ї–µ–Ї—Б–∞–љ–і—А–Є–є—Б–Ї–Є–є , –Ґ–µ–Њ–љ –°–Љ–Є—А–љ—Б–Ї–Є–є –Є –і—А—Г–≥–Є–µ. –У–Є–њ—Б–Є–Ї–ї (II –≤–µ–Ї –і–Њ –љ. —Н.) –і–∞–ї –Њ–±—Й–µ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ
k
{\displaystyle k}
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
n
{\displaystyle n}
–∞—А–Є—Д–Љ–µ—В–Є—З–µ—Б–Ї–Њ–є –њ—А–Њ–≥—А–µ—Б—Б–Є–Є , —Г –Ї–Њ—В–Њ—А–Њ–є –њ–µ—А–≤—Л–є —З–ї–µ–љ –µ—Б—В—М
1
{\displaystyle 1}
k
− вИТ -->
2
{\displaystyle k-2}
[ 12] [ 13]
–Х—Б–ї–Є –≤–Ј—П—В—М —Б–Ї–Њ–ї—М–Ї–Њ-–љ–Є–±—Г–і—М —З–Є—Б–µ–ї, –љ–∞—З–Є–љ–∞—П —Б –µ–і–Є–љ–Є—Ж—Л, –Є–Љ–µ—О—Й–Є—Е –Њ–і–Є–љ–∞–Ї–Њ–≤—Л–µ —А–∞–Ј–љ–Њ—Б—В–Є, —В–Њ —Б—Г–Љ–Љ–∞ –Є—Е, –µ—Б–ї–Є —А–∞–Ј–љ–Њ—Б—В—М –µ–і–Є–љ–Є—Ж–∞, –±—Г–і–µ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ, –µ—Б–ї–Є –ґ–µ –і–≤–Њ–є–Ї–∞, —В–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ, –∞ –µ—Б–ї–Є —В—А–Њ–є–Ї–∞ вАФ –њ—П—В–Є—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ. –Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ —Г–≥–ї–Њ–≤ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —А–∞–Ј–љ–Њ—Б—В—М—О, —Г–≤–µ–ї–Є—З–µ–љ–љ–Њ–є –љ–∞ –і–≤–Њ–є–Ї—Г, –∞ —Б—В–Њ—А–Њ–љ–∞ вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ–Љ –≤–Ј—П—В—Л—Е —З–Є—Б–µ–ї, —Б—З–Є—В–∞—П –Є –µ–і–Є–љ–Є—Ж—Г.
–Ю —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–ї–∞—Е –Љ–љ–Њ–≥–Њ –≥–Њ–≤–Њ—А–Є—В—Б—П –≤ –њ–Є—Д–∞–≥–Њ—А–µ–є—Б–Ї–Є—Е —Г—З–µ–±–љ–Є–Ї–∞—Е –∞—А–Є—Д–Љ–µ—В–Є–Ї–Є, —Б–Њ–Ј–і–∞–љ–љ—Л—Е –Э–Є–Ї–Њ–Љ–∞—Е–Њ–Љ –У–µ—А–∞–Ј—Б–Ї–Є–Љ –Є –Ґ–µ–Њ–љ–Њ–Љ –°–Љ–Є—А–љ—Б–Ї–Є–Љ (II –≤–µ–Ї), –Ї–Њ—В–Њ—А—Л–µ —Г—Б—В–∞–љ–Њ–≤–Є–ї–Є —А—П–і –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–µ–є –Љ–µ–ґ–і—Г —Д–Є–≥—Г—А–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є —А–∞–Ј–љ—Л—Е —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–µ–є. –С–Њ–ї—М—И–Њ–є –Є–љ—В–µ—А–µ—Б –Ї —Д–Є–≥—Г—А–љ—Л–Љ —З–Є—Б–ї–∞–Љ –њ—А–Њ—П–≤–Є–ї–Є –Є–љ–і–Є–є—Б–Ї–Є–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –Є –њ–µ—А–≤—Л–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є —Б—А–µ–і–љ–µ–≤–µ–Ї–Њ–≤–Њ–є –Х–≤—А–Њ–њ—Л (–§–Є–±–Њ–љ–∞—З—З–Є , –Я–∞—З–Њ–ї–Є , –Ъ–∞—А–і–∞–љ–Њ –Є –і—А.)[ 14] [ 4]
–Т –Э–Њ–≤–Њ–µ –≤—А–µ–Љ—П –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є –Ј–∞–љ–Є–Љ–∞–ї–Є—Б—М –§–µ—А–Љ–∞ , –Т–∞–ї–ї–Є—Б , –≠–є–ї–µ—А , –Ы–∞–≥—А–∞–љ–ґ , –У–∞—Г—Б—Б –Є –і—А—Г–≥–Є–µ. –Т —Б–µ–љ—В—П–±—А–µ 1636 –≥–Њ–і–∞[ 15] –Ь–µ—А—Б–µ–љ–љ—Г —В–µ–Њ—А–µ–Љ—Г, –Ї–Њ—В–Њ—А–∞—П —Б–µ–≥–Њ–і–љ—П –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —В–µ–Њ—А–µ–Љ–Њ–є –§–µ—А–Љ–∞ –Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–ї–∞—Е [ 14]
–ѓ –њ–µ—А–≤—Л–Љ –Њ—В–Ї—А—Л–ї –Њ—З–µ–љ—М –Ї—А–∞—Б–Є–≤—Г—О –Є —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ –Њ–±—Й—Г—О —В–µ–Њ—А–µ–Љ—Г –Њ —В–Њ–Љ, —З—В–Њ –Ї–∞–ґ–і–Њ–µ —З–Є—Б–ї–Њ —П–≤–ї—П–µ—В—Б—П –ї–Є–±–Њ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ, –ї–Є–±–Њ —Б—Г–Љ–Љ–Њ–є –і–≤—Г—Е –Є–ї–Є —В—А—С—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї; –Ї–∞–ґ–і–Њ–µ —З–Є—Б–ї–Њ –Є–ї–Є –Ї–≤–∞–і—А–∞—В–љ–Њ–µ, –Є–ї–Є —П–≤–ї—П–µ—В—Б—П —Б—Г–Љ–Љ–Њ–є –і–≤—Г—Е, —В—А—С—Е –Є–ї–Є —З–µ—В—Л—А—С—Е –Ї–≤–∞–і—А–∞—В–Њ–≤; –Є–ї–Є –њ—П—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ, –Є–ї–Є —П–≤–ї—П–µ—В—Б—П —Б—Г–Љ–Љ–Њ–є –і–≤—Г—Е, —В—А—С—Е, —З–µ—В—Л—А—С—Е –Є–ї–Є –њ—П—В–Є –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї, –Є —В. –і. –і–Њ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В–Є, –±—Г–і—М —В–Њ –і–ї—П —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л—Е, —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л—Е –Є–ї–Є –ї—О–±—Л—Е –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї. –ѓ –љ–µ –Љ–Њ–≥—Г –і–∞—В—М –Ј–і–µ—Б—М –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ, –Ї–Њ—В–Њ—А–Њ–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –Љ–љ–Њ–≥–Њ—З–Є—Б–ї–µ–љ–љ—Л—Е –Є –Ј–∞–њ—Г—В–∞–љ–љ—Л—Е —В–∞–є–љ —З–Є—Б–µ–ї, –Є–±–Њ —П –љ–∞–Љ–µ—А–µ–љ –њ–Њ—Б–≤—П—В–Є—В—М —Н—В–Њ–є —В–µ–Љ–µ —Ж–µ–ї—Г—О –Ї–љ–Є–≥—Г –Є –њ–Њ–ї—Г—З–Є—В—М –≤ —Н—В–Њ–є —З–∞—Б—В–Є –∞—А–Є—Д–Љ–µ—В–Є–Ї–Є —Г–і–Є–≤–Є—В–µ–ї—М–љ—Л–µ –і–Њ—Б—В–Є–ґ–µ–љ–Є—П –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б —А–∞–љ–µ–µ –Є–Ј–≤–µ—Б—В–љ—Л–Љ–Є –њ—А–µ–і–µ–ї–∞–Љ–Є.
–Т–Њ–њ—А–µ–Ї–Є –Њ–±–µ—Й–∞–љ–Є—О, –§–µ—А–Љ–∞ —В–∞–Ї –Є –љ–µ –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–ї –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ —Н—В–Њ–є —В–µ–Њ—А–µ–Љ—Л, –Ї–Њ—В–Њ—А—Г—О –≤ –њ–Є—Б—М–Љ–µ –Я–∞—Б–Ї–∞–ї—О (1654) –љ–∞–Ј–≤–∞–ї —Б–≤–Њ–Є–Љ –≥–ї–∞–≤–љ—Л–Љ –і–Њ—Б—В–Є–ґ–µ–љ–Є–µ–Љ –≤ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ[ 15] –Ы–∞–≥—А–∞–љ–ґ –і–Њ–Ї–∞–Ј–∞–ї —В–µ–Њ—А–µ–Љ—Г –і–ї—П –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї (—В–µ–Њ—А–µ–Љ–∞ –Ы–∞–≥—А–∞–љ–ґ–∞ –Њ —Б—Г–Љ–Љ–µ —З–µ—В—Л—А—С—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ ), –≤ 1796 –≥–Њ–і—Г –У–∞—Г—Б—Б –і–∞–ї –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е. –Я–Њ–ї–љ–Њ–µ –і–Њ–Ї–∞–Ј–∞—В–µ–ї—М—Б—В–≤–Њ —В–µ–Њ—А–µ–Љ—Л —Б—Г–Љ–µ–ї –і–∞—В—М –Ъ–Њ—И–Є –≤ 1813 –≥–Њ–і—Г[ 16] [ 17]
–Я–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї :
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210 вА¶,
n
(
n
+
1
)
2
{\textstyle {\frac {n(n+1)}{2}}}
A000217 –≤ OEIS ) –°–≤–Њ–є—Б—В–≤–∞ [ 18]
–І—С—В–љ–Њ—Б—В—М —Н–ї–µ–Љ–µ–љ—В–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є –Љ–µ–љ—П–µ—В—Б—П —Б –њ–µ—А–Є–Њ–і–Њ–Љ 4: –љ–µ—З—С—В–љ–Њ–µ, –љ–µ—З—С—В–љ–Њ–µ, —З—С—В–љ–Њ–µ, —З—С—В–љ–Њ–µ. –Э–Є–Ї–∞–Ї–Њ–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –љ–µ –Љ–Њ–ґ–µ—В (–≤ –і–µ—Б—П—В–Є—З–љ–Њ–є –Ј–∞–њ–Є—Б–Є) –Њ–Ї–∞–љ—З–Є–≤–∞—В—М—Б—П —Ж–Є—Д—А–∞–Љ–Є 2, 4, 7, 9[ 19]
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ –і–ї—П –Ї—А–∞—В–Ї–Њ—Б—В–Є
n
{\displaystyle n}
T
n
=
P
n
(
3
)
=
n
(
n
+
1
)
2
.
{\textstyle T_{n}=P_{n}^{(3)}={\frac {n(n+1)}{2}}.}
T
2
n
=
3
T
n
+
T
n
− вИТ -->
1
{\displaystyle T_{2n}=3T_{n}+T_{n-1}}
T
2
n
+
1
=
3
T
n
+
T
n
+
1
{\displaystyle T_{2n+1}=3T_{n}+T_{n+1}}
–§–Њ—А–Љ—Г–ї–∞ –С–∞—И–µ –і–µ –Ь–µ–Ј–Є—А–Є–∞–Ї–∞ : –Њ–±—Й—Г—О —Д–Њ—А–Љ—Г–ї—Г –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞ –Љ–Њ–ґ–љ–Њ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞—В—М —В–∞–Ї, —З—В–Њ –Њ–љ–∞ –њ–Њ–Ї–∞–ґ–µ—В –≤—Л—А–∞–ґ–µ–љ–Є–µ –ї—О–±–Њ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞ —З–µ—А–µ–Ј —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ:
P
n
(
k
)
=
n
+
(
k
− вИТ -->
2
)
n
(
n
− вИТ -->
1
)
2
=
(
k
− вИТ -->
2
)
T
n
− вИТ -->
1
+
n
=
(
k
− вИТ -->
3
)
T
n
− вИТ -->
1
+
T
n
{\textstyle P_{n}^{(k)}=n+(k-2){\frac {n(n-1)}{2}}=(k-2)T_{n-1}+n=(k-3)T_{n-1}+T_{n}}
(–С–∞—И–µ)
–°—Г–Љ–Љ–∞ –і–≤—Г—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Њ–±—А–∞–Ј—Г–µ—В –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ –°—Г–Љ–Љ–∞ –і–≤—Г—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –і–∞—С—В –њ–Њ–ї–љ—Л–є –Ї–≤–∞–і—А–∞—В (–Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ ):
T
n
+
T
n
+
1
=
(
n
+
1
)
2
=
P
n
+
1
(
4
)
{\displaystyle T_{n}+T_{n+1}=(n+1)^{2}=P_{n+1}^{(4)}}
–Ш–Ј —В–µ–Њ—А–µ–Љ—Л –§–µ—А–Љ–∞ –Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–ї–∞—Е —Б–ї–µ–і—Г–µ—В, —З—В–Њ –ї—О–±–Њ–µ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –њ—А–µ–і—Б—В–∞–≤–Є–Љ–Њ –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –љ–µ –±–Њ–ї–µ–µ —В—А—С—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї.
–°—Г–Љ–Љ–∞ –Ї–Њ–љ–µ—З–љ–Њ–≥–Њ —А—П–і–∞ —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –≤—Л—З–Є—Б–ї—П–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ:
S
m
− вИТ -->
1
=
1
+
3
+
6
+
⋯ вЛѓ -->
+
(
m
− вИТ -->
1
)
m
2
=
m
3
− вИТ -->
m
6
{\displaystyle S_{m-1}=1+3+6+\dots +{\frac {(m-1)m}{2}}={\frac {m^{3}-m}{6}}}
–†—П–і –Є–Ј —З–Є—Б–µ–ї, –Њ–±—А–∞—В–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ (—В–µ–ї–µ—Б–Ї–Њ–њ–Є—З–µ—Б–Ї–Є–є —А—П–і ), —Б—Е–Њ–і–Є—В—Б—П[ 20]
1
+
1
3
+
1
6
+
1
10
+
1
15
+
⋯ вЛѓ -->
=
2
∑ вИС -->
n
=
1
∞ вИЮ -->
(
1
n
− вИТ -->
1
n
+
1
)
=
2
{\displaystyle 1+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+\dots =2\sum _{n=1}^{\infty }\left({1 \over n}-{1 \over n+1}\right)=2}
–£–і–≤–Њ–µ–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –і–∞—О—В –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М (–Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л—Е –љ–Є–ґ–µвЮ§ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї .
–Э–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ
N
{\displaystyle N}
8
N
+
1
{\displaystyle 8N+1}
–Ї–≤–∞–і—А–∞—В–љ—Л–Љ вЮ§ [ 21]
–Ш–Ј–≤–µ—Б—В–љ–Њ–µ –≤ –Љ–Є—Б—В–Є–Ї–µ ¬Ђ—З–Є—Б–ї–Њ –Ј–≤–µ—А—П ¬ї (666) —П–≤–ї—П–µ—В—Б—П 36-–Љ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ. –Ю–љ–Њ —П–≤–ї—П–µ—В—Б—П –љ–∞–Є–Љ–µ–љ—М—И–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ —З–Є—Б–ї–Њ–Љ, –Ї–Њ—В–Њ—А–Њ–µ –њ—А–µ–і—Б—В–∞–≤–Є–Љ–Њ –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –Ї–≤–∞–і—А–∞—В–Њ–≤ —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї[ 22]
666
=
15
2
+
21
2
{\displaystyle 666=15^{2}+21^{2}}
–Ґ—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –Њ–±—А–∞–Ј—Г—О—В —В—А–µ—В—М—О –і–Є–∞–≥–Њ–љ–∞–ї—М–љ—Г—О –ї–Є–љ–Є—О —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Я–∞—Б–Ї–∞–ї—П вЮ§
–Ю—Б–љ–Њ–≤–љ–∞—П —Б—В–∞—В—М—П:
–Ъ–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ
0
+
1
=
1
{\displaystyle 0+\color {blue}1\color {black}=1}
1
+
3
=
4
{\displaystyle 1+\color {blue}3\color {black}=4}
4
+
5
=
9
{\displaystyle 4+\color {blue}5\color {black}=9}
9
+
7
=
16
{\displaystyle 9+\color {blue}7\color {black}=16}
–Ъ–≤–∞–і—А–∞—В–љ—Л–µ —З–Є—Б–ї–∞ –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В —Б–Њ–±–Њ–є –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –і–≤—Г—Е –Њ–і–Є–љ–∞–Ї–Њ–≤—Л—Е –љ–∞—В—Г—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї, —В–Њ –µ—Б—В—М —П–≤–ї—П—О—В—Б—П –њ–Њ–ї–љ—Л–Љ–Є –Ї–≤–∞–і—А–∞—В–∞–Љ–Є:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400 вА¶,
n
2
{\displaystyle n^{2}}
A000290 –≤ OEIS ). –Ъ–∞–ґ–і–Њ–µ –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ, –Ї—А–Њ–Љ–µ –µ–і–Є–љ–Є—Ж—Л, –µ—Б—В—М —Б—Г–Љ–Љ–∞ –і–≤—Г—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї[ 23]
n
2
=
T
n
− вИТ -->
1
+
T
n
{\displaystyle n^{2}=T_{n-1}+T_{n}}
4
=
1
+
3
;
9
=
3
+
6
;
16
=
6
+
10
{\displaystyle 4=1+3;\quad 9=3+6;\quad 16=6+10}
–°—Г–Љ–Љ–∞ –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ —З–Є—Б–ї–∞ —Б –њ—А–µ–і—И–µ—Б—В–≤—Г—О—Й–Є–Љ –µ–Љ—Г –њ–Њ –љ–Њ–Љ–µ—А—Г —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ —З–Є—Б–ї–Њ–Љ –і–∞—С—В –њ—П—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ :
n
2
+
T
n
− вИТ -->
1
=
P
n
(
5
)
{\displaystyle n^{2}+T_{n-1}=P_{n}^{(5)}}
–≠—В–∞ —В–µ–Њ—А–µ–Љ–∞ –±—Л–ї–∞ –≤–њ–µ—А–≤—Л–µ –Њ–њ—Г–±–ї–Є–Ї–Њ–≤–∞–љ–∞ –Э–Є–Ї–Њ–Љ–∞—Е–Њ–Љ (¬Ђ–Т–≤–µ–і–µ–љ–Є–µ –≤ –∞—А–Є—Д–Љ–µ—В–Є–Ї—Г ¬ї, II –≤–µ–Ї)[ 24]
–°—Г–Љ–Љ–∞ –Ї–≤–∞–і—А–∞—В–Њ–≤ –њ–µ—А–≤—Л—Е
n
{\displaystyle n}
[ 25]
1
2
+
2
2
+
3
2
+
.
.
.
+
n
2
=
n
(
n
+
1
)
(
2
n
+
1
)
6
{\textstyle 1^{2}+2^{2}+3^{2}+...+n^{2}={\frac {n(n+1)(2n+1)}{6}}}
–†—П–і –Њ–±—А–∞—В–љ—Л—Е –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї —Б—Е–Њ–і–Є—В—Б—П[ 26]
∑ вИС -->
n
=
1
∞ вИЮ -->
1
n
2
=
1
1
2
+
1
2
2
+
⋯ вЛѓ -->
+
1
n
2
+
⋯ вЛѓ -->
=
π ѕА -->
2
6
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\dots +{\frac {1}{n^{2}}}+\dots ={\frac {\pi ^{2}}{6}}}
–Ъ–∞–ґ–і–Њ–µ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Њ –Ї–∞–Ї —Б—Г–Љ–Љ–∞ –љ–µ –±–Њ–ї–µ–µ —З–µ—В—Л—А—С—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ (—В–µ–Њ—А–µ–Љ–∞ –Ы–∞–≥—А–∞–љ–ґ–∞ –Њ —Б—Г–Љ–Љ–µ —З–µ—В—Л—А—С—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ ).
–Ґ–Њ–ґ–і–µ—Б—В–≤–Њ –С—А–∞—Е–Љ–∞–≥—Г–њ—В—Л вАФ –§–Є–±–Њ–љ–∞—З—З–Є : –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ —Б—Г–Љ–Љ—Л –і–≤—Г—Е –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї –љ–∞ –ї—О–±—Г—О –і—А—Г–≥—Г—О —Б—Г–Љ–Љ—Г –і–≤—Г—Е –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї —Б–∞–Љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є–Љ–Њ –≤ –≤–Є–і–µ —Б—Г–Љ–Љ—Л –і–≤—Г—Е –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї.
(
a
2
+
b
2
)
(
c
2
+
d
2
)
=
(
a
c
− вИТ -->
b
d
)
2
+
(
a
d
+
b
c
)
2
=
(
a
c
+
b
d
)
2
+
(
a
d
− вИТ -->
b
c
)
2
.
{\displaystyle (a^{2}+b^{2})(c^{2}+d^{2})=(ac-bd)^{2}+(ad+bc)^{2}=(ac+bd)^{2}+(ad-bc)^{2}.}
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –≤—В–Њ—А–Њ–µ —Б–ї–∞–≥–∞–µ–Љ–Њ–µ —Б–њ—А–∞–≤–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М —А–∞–≤–љ–Њ –љ—Г–ї—О, –Ј–і–µ—Б—М —Б–ї–µ–і—Г–µ—В —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞—В—М —А–∞—Б—И–Є—А–µ–љ–љ—Л–є —А—П–і –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї, –љ–∞—З–Є–љ–∞—О—Й–Є–є—Б—П –љ–µ —Б 1, –∞ —Б –љ—Г–ї—П (—Б–Љ. A000290 ).
–Я—А–Є–Љ–µ—А:
(
1
2
+
4
2
)
(
2
2
+
7
2
)
=
26
2
+
15
2
=
30
2
+
1
2
{\displaystyle (1^{2}+4^{2})(2^{2}+7^{2})=26^{2}+15^{2}=30^{2}+1^{2}}
–Я–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Є–Љ–µ–µ—В –≤–Є–і:
1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590 вА¶,
n
(
3
n
− вИТ -->
1
)
2
{\textstyle {\frac {n(3n-1)}{2}}}
A000326 –≤ OEIS ). –Я—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —В–µ—Б–љ–Њ —Б–≤—П–Ј–∞–љ—Л —Б —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ–Є[ 24]
P
n
(
5
)
=
n
(
3
n
− вИТ -->
1
)
2
=
T
n
− вИТ -->
1
+
n
2
=
T
n
+
2
T
n
− вИТ -->
1
=
T
2
n
− вИТ -->
1
− вИТ -->
T
n
− вИТ -->
1
=
1
3
T
3
n
− вИТ -->
1
{\displaystyle P_{n}^{(5)}={\frac {n(3n-1)}{2}}=T_{n-1}+n^{2}=T_{n}+2T_{n-1}=T_{2n-1}-T_{n-1}={\frac {1}{3}}T_{3n-1}}
–Ъ–∞–Ї —Г–ґ–µ —Г–њ–Њ–Љ–Є–љ–∞–ї–Њ—Б—М –≤—Л—И–µ, –њ—П—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ, –љ–∞—З–Є–љ–∞—П —Б–Њ 2-–≥–Њ –љ–Њ–Љ–µ—А–∞, –Љ–Њ–ґ–љ–Њ –њ—А–µ–і—Б—В–∞–≤–Є—В—М –Ї–∞–Ї —Б—Г–Љ–Љ—Г –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ –Є —В—А–µ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞:
P
n
(
5
)
=
n
2
+
T
n
− вИТ -->
1
{\displaystyle P_{n}^{(5)}=n^{2}+T_{n-1}}
–Х—Б–ї–Є –≤ —Д–Њ—А–Љ—Г–ї–µ
n
(
3
n
− вИТ -->
1
)
2
{\textstyle {\frac {n(3n-1)}{2}}}
n
{\displaystyle n}
n
=
0
,
1
,
− вИТ -->
1
,
2
,
− вИТ -->
2
,
3
,
− вИТ -->
3
… вА¶ -->
{\displaystyle n=0,\;1,\;-1,\;2,\;-2,\;3,\;-3\dots }
—В–Њ –њ–Њ–ї—Г—З–∞—В—Б—П –Њ–±–Њ–±—Й—С–љ–љ—Л–µ –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ :
0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A001318 –≤ OEIS ). –Ы–µ–Њ–љ–∞—А–і –≠–є–ї–µ—А –Њ–±–љ–∞—А—Г–ґ–Є–ї –Њ–±–Њ–±—Й—С–љ–љ—Л–µ –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –≤ —Б–ї–µ–і—Г—О—Й–µ–Љ —В–Њ–ґ–і–µ—Б—В–≤–µ :
(
1
− вИТ -->
x
)
(
1
− вИТ -->
x
2
)
(
1
− вИТ -->
x
3
)
… вА¶ -->
=
1
− вИТ -->
x
− вИТ -->
x
2
+
x
5
+
x
7
− вИТ -->
x
12
− вИТ -->
x
15
+
x
22
+
x
26
− вИТ -->
x
35
− вИТ -->
x
40
+
… вА¶ -->
{\displaystyle (1-x)(1-x^{2})(1-x^{3})\ldots =1-x-x^{2}+x^{5}+x^{7}-x^{12}-x^{15}+x^{22}+x^{26}-x^{35}-x^{40}+\ldots }
–°—В–µ–њ–µ–љ–Є
x
{\displaystyle x}
[ 27]
–Я–µ—А–≤—Л–µ —З–µ—В—Л—А–µ —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–ї–∞. 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780 вА¶,
2
n
2
− вИТ -->
n
{\displaystyle 2n^{2}-n}
A000384 –≤ OEIS ). –Я–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –њ–Њ–ї—Г—З–∞–µ—В—Б—П –Є–Ј –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –≤—Л—З—С—А–Ї–Є–≤–∞–љ–Є–µ–Љ —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —Б —З—С—В–љ—Л–Љ–Є –љ–Њ–Љ–µ—А–∞–Љ–Є[ 28]
P
n
(
6
)
=
P
2
n
− вИТ -->
1
(
3
)
{\displaystyle P_{n}^{(6)}=P_{2n-1}^{(3)}}
–Э–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ
N
{\displaystyle N}
8
N
+
1
+
1
4
{\textstyle {\frac {{\sqrt {8N+1}}+1}{4}}}
вЮ§
–Ф–≤–µ–љ–∞–і—Ж–∞—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –≤—Л—З–Є—Б–ї—П—О—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ
5
n
2
− вИТ -->
4
n
{\displaystyle 5n^{2}-4n}
1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920 вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A051624 –≤ OEIS ). –Т –і–µ—Б—П—В–Є—З–љ–Њ–є —Б–Є—Б—В–µ–Љ–µ
n
{\displaystyle n}
n
{\displaystyle n}
—Б—А–∞–≤–љ–µ–љ–Є—П :
5
n
(
n
− вИТ -->
1
)
≡ вЙ° -->
0
(
mod
10
)
,
{\displaystyle 5n(n-1)\equiv 0{\pmod {10}},}
5
n
2
− вИТ -->
4
n
≡ вЙ° -->
n
(
mod
10
)
{\displaystyle 5n^{2}-4n\equiv n{\pmod {10}}}
вЦ†
–Ч–∞–і–∞—З–∞ 1 (–Ј–∞–і–∞—З–∞ –Ф–Є–Њ—Д–∞–љ—В–∞): –і–∞–љ–Њ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ
N
>
2
{\displaystyle N>2}
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
k
{\displaystyle k}
n
{\displaystyle n}
–≤—Л—П—Б–љ–Є—В—М, —Б–Ї–Њ–ї—М–Ї–Њ —А–∞–Ј –і–∞–љ–љ–Њ–µ —З–Є—Б–ї–Њ –≤—Б—В—А–µ—З–∞–µ—В—Б—П —Б—А–µ–і–Є –≤—Б–µ–≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї ¬ї[ 29]
–†–µ—И–µ–љ–Є–µ –Ј–∞–і–∞—З–Є —Б–≤–Њ–і–Є—В—Б—П –Ї —А–µ—И–µ–љ–Є—О ¬Ђ–і–Є–Њ—Д–∞–љ—В–Њ–≤–∞ —Г—А–∞–≤–љ–µ–љ–Є—П ¬ї (—Б–Љ. –Њ–±—Й—Г—О —Д–Њ—А–Љ—Г–ї—Г ):
N
=
P
n
(
k
)
=
(
k
− вИТ -->
2
)
n
2
− вИТ -->
(
k
− вИТ -->
4
)
n
2
,
{\displaystyle N=P_{n}^{(k)}={\frac {(k-2)n^{2}-(k-4)n}{2}},}
2
N
− вИТ -->
2
n
=
(
k
− вИТ -->
2
)
(
n
2
− вИТ -->
n
)
{\displaystyle 2N-2n=(k-2)(n^{2}-n)}
–Я–µ—А–µ–њ–Є—И–µ–Љ –њ–Њ–ї—Г—З–µ–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –≤ –≤–Є–і–µ:
k
− вИТ -->
2
=
2
N
− вИТ -->
2
n
− вИТ -->
1
− вИТ -->
2
N
n
{\displaystyle k-2={\frac {2N-2}{n-1}}-{\frac {2N}{n}}}
–Ч–љ–∞–Љ–µ–љ–∞—В–µ–ї–Є –і—А–Њ–±–µ–є —Б–њ—А–∞–≤–∞ –≤–Ј–∞–Є–Љ–љ–Њ –њ—А–Њ—Б—В—Л ; —Б—Г–Љ–Љ–∞ –Є–ї–Є —А–∞–Ј–љ–Њ—Б—В—М —В–∞–Ї–Є—Е –і—А–Њ–±–µ–є –Љ–Њ–ґ–µ—В –±—Л—В—М —Ж–µ–ї—Л–Љ —З–Є—Б–ї–Њ–Љ —В–Њ–ї—М–Ї–Њ –µ—Б–ї–Є –Ї–∞–ґ–і–∞—П –і—А–Њ–±—М –µ—Б—В—М —Ж–µ–ї–Њ–µ —З–Є—Б–ї–Њ[ 30]
2
N
− вИТ -->
2
{\displaystyle 2N-2}
n
− вИТ -->
1
{\displaystyle n-1}
2
N
{\displaystyle 2N}
n
{\displaystyle n}
–Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –∞–ї–≥–Њ—А–Є—В–Љ —А–µ—И–µ–љ–Є—П –њ—А–Є–Њ–±—А–µ—В–∞–µ—В —Б–ї–µ–і—Г—О—Й—Г—О —Д–Њ—А–Љ—Г[ 29]
–Т—Л–њ–Є—Б–∞—В—М –≤—Б–µ –љ–∞—В—Г—А–∞–ї—М–љ—Л–µ –і–µ–ї–Є—В–µ–ї–Є —З–Є—Б–ї–∞
2
N
{\displaystyle 2N}
1
{\displaystyle 1}
2
N
{\displaystyle 2N}
–Т—Л–њ–Є—Б–∞—В—М –≤—Б–µ –љ–∞—В—Г—А–∞–ї—М–љ—Л–µ –і–µ–ї–Є—В–µ–ї–Є —З–Є—Б–ї–∞
2
N
− вИТ -->
2
{\displaystyle 2N-2}
–Ю—В–Њ–±—А–∞—В—М –Є–Ј –њ–µ—А–≤–Њ–≥–Њ –љ–∞–±–Њ—А–∞ —В–µ —З–Є—Б–ї–∞, –Ї–Њ—В–Њ—А—Л–µ –љ–∞
1
{\displaystyle 1}
n
{\displaystyle n}
–Ф–ї—П –Ї–∞–ґ–і–Њ–≥–Њ –Њ—В–Њ–±—А–∞–љ–љ–Њ–≥–Њ
n
{\displaystyle n}
k
=
2
N
− вИТ -->
2
n
− вИТ -->
1
− вИТ -->
2
N
n
+
2
{\textstyle k={\frac {2N-2}{n-1}}-{\frac {2N}{n}}+2}
–Т—Л—З–µ—А–Ї–љ—Г—В—М –њ–∞—А—Л
(
n
,
k
)
{\displaystyle (n,\;k)}
k
<
3
{\displaystyle k<3}
–Ґ–Њ–≥–і–∞ –≤—Б–µ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–µ –Њ—Б—В–∞–≤—И–Є–Љ—Б—П –њ–∞—А–∞–Љ —З–Є—Б–ї–∞
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
N
{\displaystyle N}
–Я—А–Є–Љ–µ—А [ 29]
N
=
105
{\displaystyle N=105}
–Ф–µ–ї–Є—В–µ–ї–Є
2
N
=
210
: : -->
1
,
2
,
3
,
5
,
6
,
7
,
10
,
14
,
15
,
21
,
30
,
35
,
42
,
70
,
105
,
210
{\displaystyle 2N=210\colon \quad 1,\;2,\;3,\;5,\;6,\;7,\;10,\;14,\;15,\;21,\;30,\;35,\;42,\;70,\;105,\;210}
–Ф–µ–ї–Є—В–µ–ї–Є
2
N
− вИТ -->
2
=
208
: : -->
1
,
2
,
4
,
8
,
13
,
16
,
26
,
52
,
104
,
208
{\displaystyle 2N-2=208\colon \quad 1,\;2,\;4,\;8,\;13,\;16,\;26,\;52,\;104,\;208}
–Ю—В–±–Њ—А
n
=
2
,
3
,
5
,
14
,
105
{\displaystyle n=2,\;3,\;5,\;14,\;105}
–°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ
k
=
105
,
36
,
12
,
14
,
2
{\displaystyle k=105,\;36,\;12,\;14,\;2}
–Ю—В–≤–µ—В:
105
{\displaystyle 105}
P
2
(
105
)
,
P
3
(
36
)
,
P
5
(
12
)
,
P
14
(
14
)
{\displaystyle P_{2}^{(105)},\;P_{3}^{(36)},\;P_{5}^{(12)},\;P_{14}^{(14)}}
–Ч–∞–і–∞—З–∞ 2 : –і–∞–љ–Њ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ
N
>
2
,
{\displaystyle N>2,}
k
{\displaystyle k}
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
k
{\displaystyle k}
–Ф–ї—П —А–µ—И–µ–љ–Є—П –Љ–Њ–ґ–љ–Њ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М —В–Њ–ґ–і–µ—Б—В–≤–Њ –Ф–Є–Њ—Д–∞–љ—В–∞ [ 31]
8
(
k
− вИТ -->
2
)
P
n
(
k
)
+
(
k
− вИТ -->
4
)
2
=
(
2
n
(
k
− вИТ -->
2
)
− вИТ -->
(
k
− вИТ -->
4
)
)
2
{\displaystyle 8(k-2)P_{n}^{(k)}+(k-4)^{2}=(2n(k-2)-(k-4))^{2}}
–≠—В–Њ —В–Њ–ґ–і–µ—Б—В–≤–Њ –њ–Њ–ї—Г—З–∞–µ—В—Б—П –Є–Ј –њ—А–Є–≤–µ–і—С–љ–љ–Њ–є –≤—Л—И–µ –Њ–±—Й–µ–є —Д–Њ—А–Љ—Г–ї—Л –і–ї—П
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
–Є —А–∞–≤–љ–Њ—Б–Є–ї—М–љ–Њ –µ–є. –Ш–Ј —В–Њ–ґ–і–µ—Б—В–≤–∞ –≤—Л—В–µ–Ї–∞–µ—В —А–µ—И–µ–љ–Є–µ: –µ—Б–ї–Є
N
{\displaystyle N}
k
{\displaystyle k}
N
=
P
n
(
k
)
{\displaystyle N=P_{n}^{(k)}}
n
,
{\displaystyle n,}
8
(
k
− вИТ -->
2
)
N
+
(
k
− вИТ -->
4
)
2
{\displaystyle 8(k-2)N+(k-4)^{2}}
R
2
{\displaystyle R^{2}}
n
{\displaystyle n}
[ 31]
n
=
R
+
k
− вИТ -->
4
2
k
− вИТ -->
4
{\textstyle n={\frac {R+k-4}{2k-4}}}
–Я—А–Є–Љ–µ—А [ 31]
1540
{\displaystyle 1540}
8
(
k
− вИТ -->
2
)
N
+
(
k
− вИТ -->
4
)
2
{\displaystyle 8(k-2)N+(k-4)^{2}}
98596
=
314
2
,
{\displaystyle 98596=314^{2},}
n
=
20
,
{\displaystyle n=20,}
1540
{\displaystyle 1540}
–°—В–µ–њ–µ–љ–љ–Њ–є —А—П–і , –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л –Ї–Њ—В–Њ—А–Њ–≥–Њ вАФ
k
{\displaystyle k}
|
x
|
<
1
{\displaystyle |x|<1}
P
1
(
k
)
x
+
P
2
(
k
)
x
2
+
P
3
(
k
)
x
3
+
⋯ вЛѓ -->
=
x
(
1
+
(
k
− вИТ -->
3
)
x
)
(
1
− вИТ -->
x
)
3
{\textstyle P_{1}^{(k)}x+P_{2}^{(k)}x^{2}+P_{3}^{(k)}x^{3}+\dots ={\frac {x(1+(k-3)x)}{(1-x)^{3}}}}
–Т—Л—А–∞–ґ–µ–љ–Є–µ —Б–њ—А–∞–≤–∞ —П–≤–ї—П–µ—В—Б—П –њ—А–Њ–Є–Ј–≤–Њ–і—П—Й–µ–є —Д—Г–љ–Ї—Ж–Є–µ–є –і–ї—П –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є
k
{\displaystyle k}
[ 32]
–Р–њ–њ–∞—А–∞—В –њ—А–Њ–Є–Ј–≤–Њ–і—П—Й–Є—Е —Д—Г–љ–Ї—Ж–Є–є –њ–Њ–Ј–≤–Њ–ї—П–µ—В –њ—А–Є–Љ–µ–љ—П—В—М –≤ —В–µ–Њ—А–Є–Є —З–Є—Б–µ–ї –Є –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–µ –Љ–µ—В–Њ–і—Л –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞ . –Я—А–Є–≤–µ–і—С–љ–љ–∞—П —Д–Њ—А–Љ—Г–ї–∞ —В–∞–Ї–ґ–µ –Њ–±—К—П—Б–љ—П–µ—В –њ–Њ—П–≤–ї–µ–љ–Є–µ
k
{\displaystyle k}
–Я—А–Є
k
=
3
{\displaystyle k=3}
x
(
1
− вИТ -->
x
)
3
=
P
1
(
3
)
x
+
P
2
(
3
)
x
2
+
P
3
(
3
)
x
3
+
⋯ вЛѓ -->
+
P
n
(
3
)
x
n
+
… вА¶ -->
{\textstyle \qquad {\frac {x}{(1-x)^{3}}}=P_{1}^{(3)}x+P_{2}^{(3)}x^{2}+P_{3}^{(3)}x^{3}+\dots +P_{n}^{(3)}x^{n}+\dots }
–Я—А–Є
k
=
4
{\displaystyle k=4}
x
(
x
+
1
)
(
1
− вИТ -->
x
)
3
=
P
1
(
4
)
x
+
P
2
(
4
)
x
2
+
P
3
(
4
)
x
3
+
⋯ вЛѓ -->
+
P
n
(
4
)
x
n
+
… вА¶ -->
{\textstyle \qquad {\frac {x(x+1)}{(1-x)^{3}}}=P_{1}^{(4)}x+P_{2}^{(4)}x^{2}+P_{3}^{(4)}x^{3}+\dots +P_{n}^{(4)}x^{n}+\dots }
–Я—А–Є
k
=
5
{\displaystyle k=5}
x
(
2
x
+
1
)
(
1
− вИТ -->
x
)
3
=
P
1
(
5
)
x
+
P
2
(
5
)
x
2
+
P
3
(
5
)
x
3
+
⋯ вЛѓ -->
+
P
n
(
5
)
x
n
+
… вА¶ -->
{\textstyle \qquad {\frac {x(2x+1)}{(1-x)^{3}}}=P_{1}^{(5)}x+P_{2}^{(5)}x^{2}+P_{3}^{(5)}x^{3}+\dots +P_{n}^{(5)}x^{n}+\dots }
–Є —В. –і.
–Ф–ї—П –љ–µ–Ї–Њ—В–Њ—А—Л—Е –Ї–ї–∞—Б—Б–Њ–≤ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї —Б—Г—Й–µ—Б—В–≤—Г—О—В —Б–≤–Њ–Є, —Б–њ–µ—Ж–Є—Д–Є—З–µ—Б–Ї–Є–µ –њ—А–Њ–Є–Ј–≤–Њ–і—П—Й–Є–µ —Д—Г–љ–Ї—Ж–Є–Є. –Э–∞–њ—А–Є–Љ–µ—А, –і–ї—П –Ї–≤–∞–і—А–∞—В–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї
1
,
36
,
1225
,
41616
,
1413721
… вА¶ -->
{\displaystyle 1,\;36,\;1225,\;41616,\;1413721\dots }
[ 33]
x
(
1
+
x
)
(
1
− вИТ -->
x
)
(
1
− вИТ -->
34
x
+
x
2
)
=
x
+
36
x
2
+
1225
x
3
+
… вА¶ -->
{\textstyle {\frac {x(1+x)}{(1-x)(1-34x+x^{2})}}=x+36x^{2}+1225x^{3}+\dots }
|
x
|
<
17
− вИТ -->
12
2
{\displaystyle |x|<17-12{\sqrt {2}}}
–°—Г—Й–µ—Б—В–≤—Г–µ—В –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ ¬Ђ–Љ–љ–Њ–≥–Њ—Д–Є–≥—Г—А–љ—Л—Е¬ї (–Є–ї–Є ¬Ђ–Љ—Г–ї—М—В–Є–Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е¬ї)[ 34] –Ї–≤–∞–і—А–∞—В–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ ¬ї)[ 35]
1
,
36
,
1225
,
41616
,
1413721
… вА¶ -->
{\displaystyle 1,\;36,\;1225,\;41616,\;1413721\dots }
A001110 –≤ OEIS ).–Ґ—А–µ—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–µ—В —В–∞–Ї–ґ–µ –±—Л—В—М –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ
–њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A014979 –≤ OEIS ): 1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465вА¶; —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–≤—Б–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —Б –љ–µ—З—С—В–љ—Л–Љ –љ–Њ–Љ–µ—А–Њ–Љ);
—Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A046194 –≤ OEIS ): 1, 21, 11781, 203841, 113123361, 1957283461, 1086210502741, 18793835590881, 10429793134197921, 180458407386358101вА¶ –Є —В. –і. –Э–µ–Є–Ј–≤–µ—Б—В–љ–Њ, —Б—Г—Й–µ—Б—В–≤—Г—О—В –ї–Є —З–Є—Б–ї–∞, –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ, –Ї–≤–∞–і—А–∞—В–љ—Л–µ –Є –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ; –њ—А–Њ–≤–µ—А–Ї–∞ –љ–∞ –Ї–Њ–Љ–њ—М—О—В–µ—А–µ —З–Є—Б–µ–ї, –Љ–µ–љ—М—И–Є—Е
10
22166
,
{\displaystyle 10^{22166},}
[ 34]
–Ъ–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ
–њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A036353 –≤ OEIS ): 1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801вА¶, —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A046177 –≤ OEIS ): 1, 1225, 1413721, 1631432881, 1882672131025, 2172602007770041, 2507180834294496361, 2893284510173841030625вА¶, —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A036354 –≤ OEIS ): 1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449вА¶ –Є —В. –і.
–Я—П—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–µ—В –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –±—Л—В—М:
—И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A046180 –≤ OEIS ): 1, 40755, 1533776805, 57722156241751, 2172315626468283465, 81752926228785223683195, 3076689623521787481625080301вА¶, —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A048900 –≤ OEIS ): 1, 4347, 16701685, 64167869935, 246532939589097, 947179489733441251, 3639063353022941697757вА¶ –Є —В. –і.
–®–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ —П–≤–ї—П–µ—В—Б—П —В–∞–Ї–ґ–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ; –Њ–љ–Њ —В–∞–Ї–ґ–µ –Љ–Њ–ґ–µ—В –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –±—Л—В—М —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л–Љ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A48903 –≤ OEIS ):
1, 121771, 12625478965, 1309034909945503, 135723357520344181225, 14072069153115290487843091вА¶ –Т–Њ–Ј–Љ–Њ–ґ–љ—Л –Є –і—А—Г–≥–Є–µ —Б–Њ—З–µ—В–∞–љ–Є—П —В—А—С—Е –Є –±–Њ–ї–µ–µ —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–µ–є —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї. –Э–∞–њ—А–Є–Љ–µ—А, –Ї–∞–Ї –і–Њ–Ї–∞–Ј–∞–љ–Њ –≤—Л—И–µвЮ§
105
{\displaystyle 105}
P
5
(
12
)
,
P
14
(
14
)
,
P
3
(
36
)
,
P
2
(
105
)
.
{\displaystyle P_{5}^{(12)},\;P_{14}^{(14)},\;P_{3}^{(36)},\;P_{2}^{(105)}.}
A062712 –≤ OEIS .
k –†–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В—М
–Ю–±—Й–∞—П —Д–Њ—А–Љ—Г–ї–∞
n –°—Г–Љ–Љ–∞ –Њ–±—А–∞—В–љ—Л—Е –Ј–љ–∞—З–µ–љ–Є–є[ 36]
–Э–Њ–Љ–µ—А OEIS
1
2
3
4
5
6
7
8
9
10
3
—В—А–µ—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 + n )1
3
6
10
15
21
28
36
45
55
2
A000217
4
–Ї–≤–∞–і—А–∞—В–љ–Њ–µ
1 / 2 n 2 вИТ 0n ) = n 2 1
4
9
16
25
36
49
64
81
100
π ѕА -->
{\displaystyle \pi }
2 / 6 A000290
5
–њ—П—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ n )1
5
12
22
35
51
70
92
117
145
3
ln
вБ° -->
3
− вИТ -->
π ѕА -->
3
3
{\displaystyle 3\ln 3-{\frac {\pi {\sqrt {3}}}{3}}}
A000326
6
—И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 2n )1
6
15
28
45
66
91
120
153
190
2 ln 2
A000384
7
—Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 3n )1
7
18
34
55
81
112
148
189
235
π ѕА -->
3
1
− вИТ -->
2
5
{\displaystyle {\tfrac {\pi }{3}}{\sqrt {1-{\tfrac {2}{\sqrt {5}}}}}}
+
5
6
ln
вБ° -->
5
− вИТ -->
5
3
ln
вБ° -->
(
1
+
5
2
)
{\displaystyle +{\tfrac {5}{6}}\ln 5-{\tfrac {\sqrt {5}}{3}}\ln \left({\tfrac {1+{\sqrt {5}}}{2}}\right)}
A000566
8
–≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 4n )1
8
21
40
65
96
133
176
225
280
3 / 4
π ѕА -->
{\displaystyle \pi }
√ 3 / 12 A000567
9
–і–µ–≤—П—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 5n )1
9
24
46
75
111
154
204
261
325
1
5
(
2
ln
вБ° -->
14
+
4
cos
вБ° -->
π ѕА -->
7
ln
вБ° -->
cos
вБ° -->
3
π ѕА -->
14
{\displaystyle {\tfrac {1}{5}}(2\ln 14+4\cos {\tfrac {\pi }{7}}\ln \cos {\tfrac {3\pi }{14}}}
+
ln
вБ° -->
sin
вБ° -->
π ѕА -->
7
sin
вБ° -->
π ѕА -->
14
− вИТ -->
ln
вБ° -->
cos
вБ° -->
π ѕА -->
14
sin
вБ° -->
3
π ѕА -->
14
{\displaystyle +\ln \sin {\tfrac {\pi }{7}}\sin {\tfrac {\pi }{14}}-\ln \cos {\tfrac {\pi }{14}}\sin {\tfrac {3\pi }{14}}}
+
π ѕА -->
tg
вБ° -->
3
π ѕА -->
14
)
{\displaystyle +\pi \operatorname {tg} {\tfrac {3\pi }{14}})}
A001106 A244646
10
–і–µ—Б—П—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 6n )1
10
27
52
85
126
175
232
297
370
ln 2 +
π ѕА -->
{\displaystyle \pi }
/ 6
A001107
11
11-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 7n )1
11
30
58
95
141
196
260
333
415
A051682
12
12-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 8n )1
12
33
64
105
156
217
288
369
460
A051624
13
13-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 9n )1
13
36
70
115
171
238
316
405
505
A051865
14
14-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 10n )1
14
39
76
125
186
259
344
441
550
2 / 5 3 / 10
π ѕА -->
{\displaystyle \pi }
√ 3 / 10 A051866
15
15-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 11n )1
15
42
82
135
201
280
372
477
595
A051867
16
16-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 12n )1
16
45
88
145
216
301
400
513
640
A051868
17
17-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 13n )1
17
48
94
155
231
322
428
549
685
A051869
18
18-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 14n )1
18
51
100
165
246
343
456
585
730
4 / 7 √ 2 / 14 √ 2 +
π ѕА -->
{\displaystyle \pi }
√ 2 / 14
A051870
19
19-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 15n )1
19
54
106
175
261
364
484
621
775
A051871
20
–і–≤–∞–і—Ж–∞—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 16n )1
20
57
112
185
276
385
512
657
820
A051872
21
21-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 17n )1
21
60
118
195
291
406
540
693
865
A051873
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
вА¶
1000
1000-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 996n )1
1000
2997
5992
9985
14976
20965
27952
35937
44920
A195163
10000
10000-—Г–≥–Њ–ї—М–љ–Њ–µ
1 / 2 n 2 вИТ 9996n )1
10000
29997
59992
99985
149976
209965
279952
359937
449920
A167149
–¶–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ
k
{\displaystyle k}
k
⩾ в©Њ -->
3
{\displaystyle k\geqslant 3}
k -—Г–≥–Њ–ї—М–љ–Є–Ї —Б
k
{\displaystyle k}
k
{\displaystyle k}
k
{\displaystyle k}
[ 37]
–Я—А–Є–Љ–µ—А—Л –њ–Њ—Б—В—А–Њ–µ–љ–Є—П —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
–Ґ—А–µ—Г–≥–Њ–ї—М–љ—Л–µ
–Ъ–≤–∞–і—А–∞—В–љ—Л–µ
–Я—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ
–®–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–µ
–Ш–Ј –њ–Њ—Б—В—А–Њ–µ–љ–Є—П –≤–Є–і–љ–Њ, —З—В–Њ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –њ–Њ–ї—Г—З–∞—О—В—Б—П –Ї–∞–Ї —З–∞—Б—В–Є—З–љ—Л–µ —Б—Г–Љ–Љ—Л —Б–ї–µ–і—Г—О—Й–µ–≥–Њ —А—П–і–∞:
1
+
k
+
2
k
+
3
k
+
4
k
+
… вА¶ -->
{\displaystyle 1+k+2k+3k+4k+\dots }
k
=
4
,
{\displaystyle k=4,}
1
,
5
,
13
,
25
,
41
… вА¶ -->
{\displaystyle 1,5,13,25,41\dots }
1
+
k
(
1
+
2
+
3
+
4
+
… вА¶ -->
)
{\displaystyle 1+k(1+2+3+4+\dots )}
—В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї (—Б–Љ. –≤—Л—И–µвЮ§
k
{\displaystyle k}
k
T
n
− вИТ -->
1
+
1
{\displaystyle kT_{n-1}+1}
T
n
(
n
=
1
,
2
,
3
… вА¶ -->
)
{\displaystyle T_{n}~(n=1,\;2,\;3\dots )}
1
{\displaystyle 1}
1
+
4
+
8
+
12
… вА¶ -->
{\displaystyle 1+4+8+12\dots }
[ 38]
–Ш–Ј –њ—А–Є–≤–µ–і—С–љ–љ–Њ–є –≤—Л—И–µ —Д–Њ—А–Љ—Г–ї—Л –і–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Љ–Њ–ґ–љ–Њ –≤—Л—А–∞–Ј–Є—В—М –Њ–±—Й—Г—О —Д–Њ—А–Љ—Г–ї—Г –і–ї—П
n
{\displaystyle n}
k
{\displaystyle k}
C
n
(
k
)
{\displaystyle C_{n}^{(k)}}
[ 38]
C
n
(
k
)
=
1
+
k
n
(
n
− вИТ -->
1
)
2
=
k
n
2
− вИТ -->
k
n
+
2
2
;
n
=
1
,
2
,
3
… вА¶ -->
{\textstyle C_{n}^{(k)}=1+k{\frac {n(n-1)}{2}}={\frac {kn^{2}-kn+2}{2}};\ n=1,\;2,\;3\dots }
(–Ю–¶–§)
–Я—А–Њ–Є–Ј–≤–Њ–і—П—Й–∞—П —Д—Г–љ–Ї—Ж–Є—П –і–ї—П —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Є–Љ–µ–µ—В –≤–Є–і[ 39]
f
(
x
)
=
x
(
1
+
(
k
− вИТ -->
2
)
x
+
x
2
)
(
1
− вИТ -->
x
)
3
;
|
x
|
<
1
{\textstyle f(x)={\frac {x(1+(k-2)x+x^{2})}{(1-x)^{3}}};\quad |x|<1}
–¶–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞
n
{\displaystyle n}
C
n
(
3
)
=
3
n
2
− вИТ -->
3
n
+
2
2
{\textstyle C_{n}^{(3)}={\frac {3n^{2}-3n+2}{2}}}
–°–ї–µ–і—Б—В–≤–Є–µ (–њ—А–Є
n
>
1
{\displaystyle n>1}
C
n
(
3
)
=
3
T
n
− вИТ -->
1
+
1
{\textstyle C_{n}^{(3)}=3T_{n-1}+1}
–Я–µ—А–≤—Л–µ —Н–ї–µ–Љ–µ–љ—В—Л –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571 вА¶,
3
n
2
− вИТ -->
3
n
+
2
2
{\textstyle {\frac {3n^{2}-3n+2}{2}}}
A005448 –≤ OEIS ). –Э–µ–Ї–Њ—В–Њ—А—Л–µ —Б–≤–Њ–є—Б—В–≤–∞[ 40]
–Ъ–∞–ґ–і–Њ–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ–Њ–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ, –љ–∞—З–Є–љ–∞—П —Б 10, —П–≤–ї—П–µ—В—Б—П —Б—Г–Љ–Љ–Њ–є —В—А—С—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
C
n
(
3
)
=
P
n
(
3
)
+
P
n
− вИТ -->
1
(
3
)
+
P
n
− вИТ -->
2
(
3
)
.
{\displaystyle C_{n}^{(3)}=P_{n}^{(3)}+P_{n-1}^{(3)}+P_{n-2}^{(3)}.}
–Ш–Ј —Б–ї–µ–і—Б—В–≤–Є—П –Њ–±—Й–µ–є —Д–Њ—А–Љ—Г–ї—Л –≤–Є–і–љ–Њ, —З—В–Њ –Ї–∞–ґ–і–Њ–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ–Њ–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ
C
n
(
3
)
{\displaystyle C_{n}^{(3)}}
T
n
− вИТ -->
1
{\displaystyle T_{n-1}}
–Э–µ–Ї–Њ—В–Њ—А—Л–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П –њ—А–Њ—Б—В—Л–Љ–Є [ 10] A125602 –≤ OEIS ).
n
{\displaystyle n}
C
n
(
4
)
=
(
2
n
− вИТ -->
1
)
2
+
1
2
=
2
n
2
− вИТ -->
2
n
+
1
=
(
n
− вИТ -->
1
)
2
+
n
2
{\textstyle C_{n}^{(4)}={(2n-1)^{2}+1 \over 2}=2n^{2}-2n+1=(n-1)^{2}+n^{2}}
–Я–µ—А–≤—Л–µ —Н–ї–µ–Љ–µ–љ—В—Л –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї:
1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761 вА¶,
n
2
+
(
n
− вИТ -->
1
)
2
… вА¶ -->
{\displaystyle n^{2}+(n-1)^{2}\dots }
A001844 –≤ OEIS ). –Э–µ–Ї–Њ—В–Њ—А—Л–µ —Б–≤–Њ–є—Б—В–≤–∞[ 41]
–Ъ–∞–Ї –≤–Є–і–љ–Њ –Є–Ј –Њ–±—Й–µ–є —Д–Њ—А–Љ—Г–ї—Л , —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ–Њ–µ –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ –µ—Б—В—М —Б—Г–Љ–Љ–∞ –і–≤—Г—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е –Ї–≤–∞–і—А–∞—В–Њ–≤.
–Т—Б–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –Ї–≤–∞–і—А–∞—В–љ—Л–µ —З–Є—Б–ї–∞ –љ–µ—З—С—В–љ—Л, –Є –њ–Њ—Б–ї–µ–і–љ—П—П —Ж–Є—Д—А–∞ –≤ –Є—Е –і–µ—Б—П—В–Є—З–љ–Њ–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–Є –Љ–µ–љ—П–µ—В—Б—П –≤ —Ж–Є–Ї–ї–µ: 1-5-3-5-1.
–Т—Б–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –Ї–≤–∞–і—А–∞—В–љ—Л–µ —З–Є—Б–ї–∞ –Є –Є—Е –і–µ–ї–Є—В–µ–ї–Є –і–∞—О—В –Њ—Б—В–∞—В–Њ–Ї 1 –њ—А–Є –і–µ–ї–µ–љ–Є–Є –љ–∞ 4, –∞ –њ—А–Є –і–µ–ї–µ–љ–Є–Є –љ–∞ 6, 8 –Є–ї–Є 12 –і–∞—О—В –Њ—Б—В–∞—В–Њ–Ї 1 –Є–ї–Є 5.
–Т—Б–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –Ї–≤–∞–і—А–∞—В–љ—Л–µ —З–Є—Б–ї–∞, –Ј–∞ –Є—Б–Ї–ї—О—З–µ–љ–Є–µ–Љ 1, –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В –і–ї–Є–љ—Г –≥–Є–њ–Њ—В–µ–љ—Г–Ј—Л –≤ –Њ–і–љ–Њ–є –Є–Ј –њ–Є—Д–∞–≥–Њ—А–Њ–≤—Л—Е —В—А–Њ–µ–Ї (–љ–∞–њ—А–Є–Љ–µ—А, 3-4-5, 5-12-13). –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Ї–∞–ґ–і–Њ–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ–Њ–µ –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ —А–∞–≤–љ–Њ —З–Є—Б–ї—Г —В–Њ—З–µ–Ї –≤–љ—Г—В—А–Є –і–∞–љ–љ–Њ–≥–Њ —А–∞—Б—Б—В–Њ—П–љ–Є—П –≤ –Ї–≤–∞—А—В–∞–ї–∞—Е –Њ—В —Ж–µ–љ—В—А–∞–ї—М–љ–Њ–є —В–Њ—З–Ї–Є –љ–∞ –Ї–≤–∞–і—А–∞—В–љ–Њ–є —А–µ—И—С—В–Ї–µ.
–†–∞–Ј–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л–Љ–Є –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ–Є –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є –µ—Б—В—М —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ–Њ–µ –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ.
–Э–µ–Ї–Њ—В–Њ—А—Л–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –Ї–≤–∞–і—А–∞—В–љ—Л–µ —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П –њ—А–Њ—Б—В—Л–Љ–Є (–Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –≤—Л—И–µ, –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–µ –Ї–≤–∞–і—А–∞—В–љ—Л–µ —З–Є—Б–ї–∞, –љ–∞—З–Є–љ–∞—П —Б —В—А–µ—В—М–µ–≥–Њ –њ–Њ –њ–Њ—А—П–і–Ї—Г, –Ј–∞–≤–µ–і–Њ–Љ–Њ —Б–Њ—Б—В–∞–≤–љ—Л–µ). –Я—А–Є–Љ–µ—А—Л –њ—А–Њ—Б—В—Л—Е —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї: 5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613 вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A027862 –≤ OEIS ).
–¶–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞
n
{\displaystyle n}
C
n
(
5
)
=
5
(
n
− вИТ -->
1
)
2
+
5
(
n
− вИТ -->
1
)
+
2
2
{\textstyle C_{n}^{(5)}={\frac {5(n-1)^{2}+5(n-1)+2}{2}}}
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л—Е —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951 вА¶,
5
(
n
− вИТ -->
1
)
2
+
5
(
n
− вИТ -->
1
)
+
2
2
{\textstyle {\frac {5(n-1)^{2}+5(n-1)+2}{2}}}
A005891 –≤ OEIS ) –І—С—В–љ–Њ—Б—В—М —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Љ–µ–љ—П–µ—В—Б—П –њ–Њ –њ—А–∞–≤–Є–ї—Г: —З—С—В–љ–Њ–µ-—З—С—В–љ–Њ–µ-–љ–µ—З—С—В–љ–Њ–µ-–љ–µ—З—С—В–љ–Њ–µ, –Є –њ–Њ—Б–ї–µ–і–љ—П—П –і–µ—Б—П—В–Є—З–љ–∞—П —Ж–Є—Д—А–∞ –Љ–µ–љ—П–µ—В—Б—П –≤ —Ж–Є–Ї–ї–µ: 6-6-1-1.
–Э–µ–Ї–Њ—В–Њ—А—Л–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –њ—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П –њ—А–Њ—Б—В—Л–Љ–Є [ 10] A145838 –≤ OEIS ).
–Я—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ —Д–Њ—А–Љ—Г–ї—Л –≤ –≤–Є–і–µ
1
+
6
(
n
(
n
− вИТ -->
1
)
2
{\textstyle 1+{\frac {6(n(n-1)}{2}}}
n
{\displaystyle n}
(
n
− вИТ -->
1
)
{\displaystyle (n-1)}
n
{\displaystyle n}
C
n
(
6
)
=
n
3
− вИТ -->
(
n
− вИТ -->
1
)
3
=
3
n
(
n
− вИТ -->
1
)
+
1
{\displaystyle C_{n}^{(6)}=n^{3}-(n-1)^{3}=3n(n-1)+1}
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л—Е —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919 вА¶
1
+
3
n
(
n
− вИТ -->
1
)
{\displaystyle 1+3n(n-1)}
A003215 –≤ OEIS ). –Э–µ–Ї–Њ—В–Њ—А—Л–µ —Б–≤–Њ–є—Б—В–≤–∞[ 42]
–Я–Њ—Б–ї–µ–і–љ–Є–є –і–µ—Б—П—В–Є—З–љ—Л–є –Ј–љ–∞–Ї —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Љ–µ–љ—П–µ—В—Б—П –≤ —Ж–Є–Ї–ї–µ 1-7-9-7-1.
–°—Г–Љ–Љ–∞ –њ–µ—А–≤—Л—Е n —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї —А–∞–≤–љ–∞ ¬Ђ–Ї—Г–±–Є—З–µ—Б–Ї–Њ–Љ—Г —З–Є—Б–ї—Г ¬ї
n
3
{\displaystyle n^{3}}
–°–њ—А–∞–≤–µ–і–ї–Є–≤–Њ —А–µ–Ї—Г—А—А–µ–љ—В–љ–Њ–µ —А–∞–≤–µ–љ—Б—В–≤–Њ:
C
n
(
6
)
=
2
C
n
− вИТ -->
1
(
6
)
− вИТ -->
C
n
− вИТ -->
2
(
6
)
+
6
{\displaystyle C_{n}^{(6)}=2C_{n-1}^{(6)}-C_{n-2}^{(6)}+6}
–Э–µ–Ї–Њ—В–Њ—А—Л–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П –њ—А–Њ—Б—В—Л–Љ–Є[ 10] A002407 –≤ OEIS ).
n
{\displaystyle n}
7
n
2
− вИТ -->
7
n
+
2
2
{\textstyle {\frac {7n^{2}-7n+2}{2}}}
(
n
− вИТ -->
1
)
{\displaystyle (n-1)}
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л—Е —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953 вА¶,
7
n
2
− вИТ -->
7
n
+
2
2
{\textstyle {\frac {7n^{2}-7n+2}{2}}}
A069099 –≤ OEIS ). –І—С—В–љ–Њ—Б—В—М —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Љ–µ–љ—П–µ—В—Б—П –≤ —Ж–Є–Ї–ї–µ –љ–µ—З—С—В–љ—Л–є-—З—С—В–љ—Л–є-—З—С—В–љ—Л–є-–љ–µ—З—С—В–љ—Л–є.
–Э–µ–Ї–Њ—В–Њ—А—Л–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П –њ—А–Њ—Б—В—Л–Љ–Є[ 10]
43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697 вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A144974 –≤ OEIS ). –°—Г—Й–µ—Б—В–≤—Г—О—В —В–∞–Ї–ґ–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ —Б–µ–Љ–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞, –≤—Е–Њ–і—П—Й–Є–µ –≤ –њ–∞—А—Л –њ—А–Њ—Б—В—Л—Е —З–Є—Б–µ–ї-–±–ї–Є–Ј–љ–µ—Ж–Њ–≤ :
43, 71, 197, 463, 1933, 5741, 8233, 9283, 11173, 14561, 34651 вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A144975 –≤ OEIS ).
n
{\displaystyle n}
(
2
n
− вИТ -->
1
)
2
=
4
n
2
− вИТ -->
4
n
+
1
{\displaystyle (2n-1)^{2}=4n^{2}-4n+1}
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л—Е —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089. –Э–µ–Ї–Њ—В–Њ—А—Л–µ —Б–≤–Њ–є—Б—В–≤–∞[ 43]
–Т—Б–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –љ–µ—З—С—В–љ—Л, –Є –Є—Е –њ–Њ—Б–ї–µ–і–љ—П—П –і–µ—Б—П—В–Є—З–љ–∞—П —Ж–Є—Д—А–∞ –Љ–µ–љ—П–µ—В—Б—П –≤ —Ж–Є–Ї–ї–µ 1-9-5-9-1.
–¶–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ–Њ–µ –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ —Б–Њ–≤–њ–∞–і–∞–µ—В —Б –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ –Ї–≤–∞–і—А–∞—В–љ—Л–Љ —З–Є—Б–ї–Њ–Љ —Б –љ–µ—З—С—В–љ—Л–Љ –љ–Њ–Љ–µ—А–Њ–Љ:
C
n
(
6
)
=
P
2
n
− вИТ -->
1
(
4
)
.
{\displaystyle C_{n}^{(6)}=P_{2n-1}^{(4)}.}
–Ш–Ј –њ—А–µ–і—Л–і—Г—Й–µ–≥–Њ —Б–≤–Њ–є—Б—В–≤–∞ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –≤—Б–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞, –Ї—А–Њ–Љ–µ 1, —Б–Њ—Б—В–∞–≤–љ—Л–µ.
n
{\displaystyle n}
(
3
n
− вИТ -->
2
)
(
3
n
− вИТ -->
1
)
2
{\displaystyle {\frac {(3n-2)(3n-1)}{2}}}
–£–Љ–љ–Њ–ґ–∞—П
(
n
− вИТ -->
1
)
{\displaystyle (n-1)}
n
{\displaystyle n}
C
n
(
9
)
=
P
3
n
− вИТ -->
2
(
3
)
{\displaystyle C_{n}^{(9)}=P_{3n-2}^{(3)}}
–Я–µ—А–≤—Л–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –і–µ–≤—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞:
1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946 вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A060544 –≤ OEIS ). –Ч–∞ –Є—Б–Ї–ї—О—З–µ–љ–Є–µ–Љ 6, –≤—Б–µ —З—С—В–љ—Л–µ —Б–Њ–≤–µ—А—И–µ–љ–љ—Л–µ —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П —В–∞–Ї–ґ–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є –і–µ–≤—П—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є. –Т 1850-–Љ –≥–Њ–і—Г –Љ–∞—В–µ–Љ–∞—В–Є–Ї-–ї—О–±–Є—В–µ–ї—М –§—А–µ–і–µ—А–Є–Ї –Я–Њ–ї–ї–Њ–Ї –≤—Л—Б–Ї–∞–Ј–∞–ї –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ , –Ї–Њ—В–Њ—А–Њ–µ –і–Њ —Б–Є—Е –њ–Њ—А –љ–µ –і–Њ–Ї–∞–Ј–∞–љ–Њ –Є –љ–µ –Њ–њ—А–Њ–≤–µ—А–≥–љ—Г—В–Њ, —З—В–Њ –ї—О–±–Њ–µ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –µ—Б—В—М —Б—Г–Љ–Љ–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ –Њ–і–Є–љ–љ–∞–і—Ж–∞—В–Є —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –і–µ–≤—П—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї[ 44]
–Ш–Ј –Њ–±—Й–µ–є —Д–Њ—А–Љ—Г–ї—Л —Б–ї–µ–і—Г–µ—В, —З—В–Њ –≤—Б–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –і–µ–≤—П—В–Є—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞, –Ї—А–Њ–Љ–µ 1, —Б–Њ—Б—В–∞–≤–љ—Л–µ.
n
{\displaystyle n}
5
(
n
2
− вИТ -->
n
)
+
1
{\displaystyle 5(n^{2}-n)+1}
–Я–µ—А–≤—Л–µ –њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї–Є —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –і–µ—Б—П—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051 вА¶
5
(
n
2
− вИТ -->
n
)
+
1
{\displaystyle 5(n^{2}-n)+1}
A062786 –≤ OEIS ). –Я–Њ–і–Њ–±–љ–Њ –і—А—Г–≥–Є–Љ k -—Г–≥–Њ–ї—М–љ—Л–Љ —З–Є—Б–ї–∞–Љ,
n
{\displaystyle n}
(
n
− вИТ -->
1
)
{\displaystyle (n-1)}
k
{\displaystyle k}
–І–∞—Б—В—М —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л—Е –і–µ—Б—П—В–Є—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї —П–≤–ї—П—О—В—Б—П –њ—А–Њ—Б—В—Л–Љ–Є, –љ–∞–њ—А–Є–Љ–µ—А:
11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A090562 –≤ OEIS ).
–Э–µ–Ї–Њ—В–Њ—А—Л–µ —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —Б–Њ–≤–њ–∞–і–∞—О—В —Б –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ–Є, –љ–∞–њ—А–Є–Љ–µ—А:
1
,
10
,
25
,
51
{\displaystyle 1,\;10,\;25,\;51}
–і–≤–Њ–є–љ—Л–Љ–Є .
1. –Ф–≤–Њ–є–љ—Л–µ —З–Є—Б–ї–∞ —Б –Њ–±—Й–Є–Љ –њ–∞—А–∞–Љ–µ—В—А–Њ–Љ
k
{\displaystyle k}
[ 45]
C
k
(
k
)
=
P
k
+
1
(
k
)
{\displaystyle C_{k}^{(k)}=P_{k+1}^{(k)}\quad }
2. –Ф–≤–Њ–є–љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —Б —А–∞–Ј–љ—Л–Љ–Є
k
.
{\displaystyle k.}
1
,
10
,
136
,
1891
,
26335
… вА¶ -->
{\displaystyle 1,\;10,\;136,\;1891,\;26335\dots }
A128862 –≤ OEIS ). –Ф–ї—П –Є—Е –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –љ–∞–і–Њ —А–µ—И–Є—В—М –і–Є–Њ—Д–∞–љ—В–Њ–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ :
m
2
+
m
=
3
n
2
− вИТ -->
3
n
+
2
,
{\displaystyle m^{2}+m=3n^{2}-3n+2,}
P
m
(
3
)
=
C
n
(
3
)
{\displaystyle P_{m}^{(3)}=C_{n}^{(3)}}
m
=
1
,
4
,
16
,
61
,
229
… вА¶ -->
{\displaystyle m=1,\;4,\;16,\;61,\;229\dots }
A133161 –≤ OEIS ), —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ:
n
=
1
,
3
,
10
,
36
,
133
… вА¶ -->
{\displaystyle n=1,\;3,\;10,\;36,\;133\dots }
A102871 –≤ OEIS ).
3. –Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–µ –Ї–≤–∞–і—А–∞—В–љ—Л–µ, —П–≤–ї—П—О—Й–Є–µ—Б—П —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є. –Ш—Е –Њ–њ—А–µ–і–µ–ї—П–µ—В –і–Є–Њ—Д–∞–љ—В–Њ–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ:
m
2
=
3
n
2
− вИТ -->
3
n
+
2
2
.
{\textstyle m^{2}={\frac {3n^{2}-3n+2}{2}}.\quad }
C
m
(
3
)
=
P
n
(
4
)
{\displaystyle C_{m}^{(3)}=P_{n}^{(4)}}
–†–µ—И–µ–љ–Є—П:
m
=
1
,
2
,
8
,
19
,
79
… вА¶ -->
{\displaystyle m=1,\;2,\;8,\;19,\;79\dots }
A129445 –≤ OEIS ), —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ
n
=
1
,
2
,
7
,
16
,
65
… вА¶ -->
{\displaystyle n=1,2,7,16,65\dots }
–Я–µ—А–≤—Л–µ —В–∞–Ї–Є–µ —З–Є—Б–ї–∞:
1
,
4
,
64
,
361
,
6241
… вА¶ -->
{\displaystyle 1,\;4,\;64,\;361,\;6241\dots }
4. –Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ, —П–≤–ї—П—О—Й–Є–µ—Б—П —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є. –Я–µ—А–≤—Л–µ —В–∞–Ї–Є–µ —З–Є—Б–ї–∞:
1
,
91
,
8911
,
873181
,
85562821
… вА¶ -->
{\displaystyle 1,\;91,\;8911,\;873181,\;85562821\dots }
A006244 –≤ OEIS ). –Ш—Е –Њ–њ—А–µ–і–µ–ї—П–µ—В –і–Є–Њ—Д–∞–љ—В–Њ–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ:
m
(
m
+
1
)
2
=
3
n
2
+
3
n
+
1.
{\displaystyle {\frac {m(m+1)}{2}}=3n^{2}+3n+1.\quad }
P
m
(
3
)
=
C
n
+
1
(
6
)
{\displaystyle P_{m}^{(3)}=C_{n+1}^{(6)}}
–†–µ—И–µ–љ–Є—П:
m
=
1
,
13
,
133
,
1321
,
13081
… вА¶ -->
{\displaystyle m=1,13,133,1321,13081\dots }
A031138 –≤ OEIS );
n
=
0
,
5
,
54
,
539
,
5340
… вА¶ -->
{\displaystyle n=0,\;5,\;54,\;539,\;5340\dots }
A087125, –≤ OEIS ).
5. –Ъ–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–µ –Ї–≤–∞–і—А–∞—В–љ—Л–µ, —П–≤–ї—П—О—Й–Є–µ—Б—П —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є. –Я–µ—А–≤—Л–µ —В–∞–Ї–Є–µ —З–Є—Б–ї–∞:
1
,
169
,
32761
,
6355441
,
1232922769
… вА¶ -->
{\displaystyle 1,\;169,\;32761,\;6355441,\;1232922769\dots }
A006051 –≤ OEIS ). –Ш—Е –Њ–њ—А–µ–і–µ–ї—П–µ—В –і–Є–Њ—Д–∞–љ—В–Њ–≤–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ:
m
2
=
3
n
2
+
3
n
+
1.
{\displaystyle m^{2}=3n^{2}+3n+1.\quad }
P
m
(
4
)
=
C
n
+
1
(
6
)
{\displaystyle P_{m}^{(4)}=C_{n+1}^{(6)}}
–†–µ—И–µ–љ–Є—П:
m
=
1
,
13
,
181
,
2521
,
35113
… вА¶ -->
{\displaystyle m=1,\;13,\;181,\;2521,\;35113\dots }
A001570 –≤ OEIS );
n
=
0
,
7
,
104
,
1455
,
20272
… вА¶ -->
{\displaystyle n=0,\;7,\;104,\;1455,\;20272\dots }
A001921, –≤ OEIS ).
–Э–∞—А—П–і—Г —Б —А–∞—Б—Б–Љ–Њ—В—А–µ–љ–љ—Л–Љ–Є –≤—Л—И–µ —Д–Є–≥—Г—А–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є –і–ї—П –њ–ї–Њ—Б–Ї–Є—Е —Д–Є–≥—Г—А, –Љ–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Л–µ –Є–ї–Є –і–∞–ґ–µ –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л–µ –Є—Е –∞–љ–∞–ї–Њ–≥–Є. –£–ґ–µ –∞–љ—В–Є—З–љ—Л–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –Є—Б—Б–ї–µ–і–Њ–≤–∞–ї–Є —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–µ –Є –Ї–≤–∞–і—А–∞—В–љ—Л–µ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞. –Э–µ—Б–ї–Њ–ґ–љ–Њ –Њ–њ—А–µ–і–µ–ї–Є—В—М —З–Є—Б–ї–∞, —Б–≤—П–Ј–∞–љ–љ—Л–µ —Б –њ–Є—А–∞–Љ–Є–і–∞–Љ–Є , –≤ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А—Л—Е –ї–µ–ґ–Є—В –ї—О–±–Њ–є –і—А—Г–≥–Њ–є –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї, –љ–∞–њ—А–Є–Љ–µ—А:
–Ф—А—Г–≥–Є–µ —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–љ—Л—Е —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї —Б–≤—П–Ј–∞–љ—Л —Б –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Є–Љ–Є –Љ–љ–Њ–≥–Њ–≥—А–∞–љ–љ–Є–Ї–∞–Љ–Є .
–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞:
Π ќ† -->
4
(
4
)
=
1
+
4
+
9
+
16
=
30
{\displaystyle \Pi _{4}^{(4)}=1+4+9+16=30}
–Я–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –Њ–њ—А–µ–і–µ–ї—П—О—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ
Π ќ† -->
n
(
k
)
{\displaystyle \Pi _{n}^{(k)}}
n
{\displaystyle n}
P
n
(
k
)
{\displaystyle P_{n}^{(k)}}
–Я–Њ –Є–љ–і—Г–Ї—Ж–Є–Є –љ–µ—В—А—Г–і–љ–Њ –і–Њ–Ї–∞–Ј–∞—В—М –Њ–±—Й—Г—О —Д–Њ—А–Љ—Г–ї—Г –і–ї—П –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞, –Є–Ј–≤–µ—Б—В–љ—Г—О –µ—Й—С –Р—А—Е–Є–Љ–µ–і—Г [ 46]
Π ќ† -->
n
(
k
)
=
n
(
n
+
1
)
(
(
k
− вИТ -->
2
)
n
− вИТ -->
k
+
5
)
6
{\displaystyle \Pi _{n}^{(k)}={\frac {n(n+1)((k-2)n-k+5)}{6}}}
(–Ю–Я–§)
–Я—А–∞–≤—Г—О —З–∞—Б—В—М —Н—В–Њ–є —Д–Њ—А–Љ—Г–ї—Л –Љ–Њ–ґ–љ–Њ —В–∞–Ї–ґ–µ –≤—Л—А–∞–Ј–Є—В—М —З–µ—А–µ–Ј –њ–ї–Њ—Б–Ї–Є–µ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞:
Π ќ† -->
n
(
k
)
=
(
k
− вИТ -->
2
)
n
− вИТ -->
k
+
5
3
P
n
(
3
)
=
n
+
1
6
(
2
P
n
(
k
)
+
n
)
{\displaystyle \Pi _{n}^{(k)}={\frac {(k-2)n-k+5}{3}}P_{n}^{(3)}={\frac {n+1}{6}}(2P_{n}^{(k)}+n)}
–°—Г—Й–µ—Б—В–≤—Г–µ—В —В—А—С—Е–Љ–µ—А–љ—Л–є –∞–љ–∞–ї–Њ–≥ —Д–Њ—А–Љ—Г–ї—Л –Э–Є–Ї–Њ–Љ–∞—Е–∞ –і–ї—П –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї[ 47]
Π ќ† -->
n
(
k
+
1
)
=
Π ќ† -->
n
(
k
)
+
Π ќ† -->
n
− вИТ -->
1
(
3
)
{\displaystyle \Pi _{n}^{(k+1)}=\Pi _{n}^{(k)}+\Pi _{n-1}^{(3)}}
–Я—А–Њ–Є–Ј–≤–Њ–і—П—Й–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Є–Љ–µ–µ—В –≤–Є–і[ 48]
f
(
x
)
=
x
(
1
+
(
k
− вИТ -->
3
)
x
)
(
1
− вИТ -->
x
)
4
;
|
x
|
<
1
{\displaystyle f(x)={\frac {x(1+(k-3)x)}{(1-x)^{4}}};\quad |x|<1}
–Ґ–µ—В—А–∞—Н–і—А —Б –і–ї–Є–љ–Њ–є —Б—В–Њ—А–Њ–љ—Л 5 —Б–Њ–і–µ—А–ґ–Є—В 35 —Б—Д–µ—А. –Ъ–∞–ґ–і—Л–є —Б–ї–Њ–є –њ—А–µ–і—Б—В–∞–≤–ї—П–µ—В –Њ–і–љ–Њ –Є–Ј –њ–µ—А–≤—Л—Е –њ—П—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Ґ—А–µ—Г–≥–Њ–ї—М–љ—Л–µ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞, –љ–∞–Ј—Л–≤–∞–µ–Љ—Л–µ —В–∞–Ї–ґ–µ —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–Љ–Є вАФ —Н—В–Њ —Д–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞, –Ї–Њ—В–Њ—А—Л–µ –њ—А–µ–і—Б—В–∞–≤–ї—П—О—В —В–µ—В—А–∞—Н–і—А , —В–Њ –µ—Б—В—М –њ–Є—А–∞–Љ–Є–і—Г, –≤ –Њ—Б–љ–Њ–≤–∞–љ–Є–Є –Ї–Њ—В–Њ—А–Њ–є –ї–µ–ґ–Є—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї. –°–Њ–≥–ї–∞—Б–љ–Њ –њ—А–Є–≤–µ–і–µ–љ–љ–Њ–Љ—Г –≤—Л—И–µ –Њ–±—Й–µ–Љ—Г –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї,
n
− вИТ -->
{\displaystyle n-}
n
{\displaystyle n}
—В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї :
Π ќ† -->
n
(
3
)
=
T
1
+
T
2
+
⋯ вЛѓ -->
+
T
n
{\displaystyle \Pi _{n}^{(3)}=T_{1}+T_{2}+\dots +T_{n}}
–Ю–±—Й–∞—П —Д–Њ—А–Љ—Г–ї–∞ –і–ї—П —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞:
Π ќ† -->
n
(
3
)
=
n
(
n
+
1
)
(
n
+
2
)
6
{\displaystyle \Pi _{n}^{(3)}={\frac {n(n+1)(n+2)}{6}}}
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л—Е —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї:
1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969 вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A000292 –≤ OEIS ). –Ш–љ—В–µ—А–µ—Б–љ–Њ, —З—В–Њ –њ—П—В–Њ–µ —З–Є—Б–ї–Њ —А–∞–≤–љ–Њ —Б—Г–Љ–Љ–µ –≤—Б–µ—Е –њ—А–µ–і—Л–і—Г—Й–Є—Е.
–°—Г—Й–µ—Б—В–≤—Г–µ—В —В—А—С—Е–Љ–µ—А–љ—Л–є –∞–љ–∞–ї–Њ–≥ —Д–Њ—А–Љ—Г–ї—Л –С–∞—И–µ –і–µ –Ь–µ–Ј–Є—А–Є–∞–Ї–∞ , –∞ –Є–Љ–µ–љ–љ–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ–≥–Њ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞ –њ–Њ —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–Љ[ 47]
Π ќ† -->
n
(
k
)
=
Π ќ† -->
n
(
3
)
+
(
k
− вИТ -->
3
)
Π ќ† -->
n
− вИТ -->
1
(
3
)
{\displaystyle \Pi _{n}^{(k)}=\Pi _{n}^{(3)}+(k-3)\Pi _{n-1}^{(3)}}
–Я—П—В—М —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ —П–≤–ї—П—О—В—Б—П —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ–Є (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A027568 –≤ OEIS ):
1, 10, 120, 1540, 7140. –Ґ–Њ–ї—М–Ї–Њ —В—А–Є —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л—Е —З–Є—Б–ї–∞ —П–≤–ї—П—О—В—Б—П –Ї–≤–∞–і—А–∞—В–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A003556 –≤ OEIS ):
1
2
=
1
{\displaystyle 1^{2}=1}
2
2
=
4
{\displaystyle 2^{2}=4}
140
2
=
19
600
{\displaystyle 140^{2}=19\,600}
–Ю–і–љ–∞ –Є–Ј ¬Ђ–≥–Є–њ–Њ—В–µ–Ј –Я–Њ–ї–ї–Њ–Ї–∞ ¬ї (1850 –≥–Њ–і): –Ї–∞–ґ–і–Њ–µ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –њ—А–µ–і—Б—В–∞–≤–Є–Љ–Њ –Ї–∞–Ї —Б—Г–Љ–Љ–∞ –љ–µ –±–Њ–ї–µ–µ –њ—П—В–Є —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї. –Ф–Њ —Б–Є—Е –њ–Њ—А –љ–µ –і–Њ–Ї–∞–Ј–∞–љ–∞, —Е–Њ—В—П –њ—А–Њ–≤–µ—А–µ–љ–∞ –і–ї—П –≤—Б–µ—Е —З–Є—Б–µ–ї, –Љ–µ–љ—М—И–Є—Е 10 –Љ–Є–ї–ї–Є–∞—А–і–Њ–≤[ 49] [ 50]
–Ъ–≤–∞–і—А–∞—В–љ—Л–µ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞ —З–∞—Б—В–Њ –Ї—А–∞—В–Ї–Њ –љ–∞–Ј—Л–≤–∞—О—В –њ—А–Њ—Б—В–Њ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–Љ–Є. –Ф–ї—П –љ–Є—Е –њ–Є—А–∞–Љ–Є–і–∞ –Є–Љ–µ–µ—В –Ї–≤–∞–і—А–∞—В–љ–Њ–µ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ. –Э–∞—З–∞–ї—М–љ–∞—П –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М:
1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819вА¶ (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A000330 –≤ OEIS ). –Ю–±—Й–∞—П —Д–Њ—А–Љ—Г–ї–∞ –і–ї—П –Ї–≤–∞–і—А–∞—В–љ–Њ–≥–Њ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ–Њ–≥–Њ —З–Є—Б–ї–∞:
Π ќ† -->
n
(
4
)
=
n
(
n
+
1
)
(
2
n
+
1
)
6
{\displaystyle \Pi _{n}^{(4)}={\frac {n(n+1)(2n+1)}{6}}}
–Ъ–≤–∞–і—А–∞—В–љ–Њ–µ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ
Π ќ† -->
n
(
4
)
{\displaystyle \Pi _{n}^{(4)}}
[ 51]
n
× √Ч -->
n
{\displaystyle n\times n}
–Ь–µ–ґ–і—Г –Ї–≤–∞–і—А–∞—В–љ—Л–Љ–Є –Є —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ–Є –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є —Б—Г—Й–µ—Б—В–≤—Г–µ—В —Б–ї–µ–і—Г—О—Й–∞—П –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М[ 52]
4
Π ќ† -->
n
(
4
)
=
Π ќ† -->
2
n
(
3
)
{\displaystyle 4\Pi _{n}^{(4)}=\Pi _{2n}^{(3)}}
–Т—Л—И–µ –±—Л–ї–Њ –Њ—В–Љ–µ—З–µ–љ–Њ, —З—В–Њ —Б—Г–Љ–Љ–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –µ—Б—В—М –Ї–≤–∞–і—А–∞—В–љ–Њ–µ —З–Є—Б–ї–Њ; –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ —Б—Г–Љ–Љ–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї –µ—Б—В—М –Ї–≤–∞–і—А–∞—В–љ–Њ–µ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ[ 52]
Π ќ† -->
n
(
4
)
=
Π ќ† -->
n
(
3
)
+
Π ќ† -->
n
− вИТ -->
1
(
3
)
{\displaystyle \Pi _{n}^{(4)}=\Pi _{n}^{(3)}+\Pi _{n-1}^{(3)}}
–Я–Њ –∞–љ–∞–ї–Њ–≥–Є–Є —Б –Ї–≤–∞–і—А–∞—В–љ—Л–Љ–Є –Љ–Њ–ґ–љ–Њ –≤–≤–µ—Б—В–Є ¬Ђ–Ї—Г–±–Є—З–µ—Б–Ї–Є–µ —З–Є—Б–ї–∞¬ї
Q
n
=
n
3
,
{\displaystyle Q_{n}=n^{3},}
–њ–ї–∞—В–Њ–љ–Њ–≤—Л–Љ —В–µ–ї–∞–Љ :
–Я—А–µ–і—Г—Б–Љ–Њ—В—А–µ–љ—Л —В–∞–Ї–ґ–µ –Є—Е —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–µ –≤–∞—А–Є–∞–љ—В—Л.
–Ю—Б–љ–Њ–≤–љ–∞—П —Б—В–∞—В—М—П:
–Ъ—Г–± (–∞–ї–≥–µ–±—А–∞) –Ъ—Г–±–Є—З–µ—Б–Ї–Є–µ —З–Є—Б–ї–∞
Q
n
{\displaystyle Q_{n}}
Q
n
=
n
3
.
{\displaystyle Q_{n}=n^{3}.}
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000 . . . (–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A000578 –≤ OEIS ). –Ъ—Г–±–Є—З–µ—Б–Ї–Њ–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–љ–Њ –≤—Л—А–∞–Ј–Є—В—М –Ї–∞–Ї —А–∞–Ј–љ–Њ—Б—В—М –Ї–≤–∞–і—А–∞—В–Њ–≤ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї[ 53]
Q
n
=
(
T
n
)
2
− вИТ -->
(
T
n
− вИТ -->
1
)
2
{\displaystyle Q_{n}=(T_{n})^{2}-(T_{n-1})^{2}}
n
⩾ в©Њ -->
2
{\displaystyle n\geqslant 2}
–°–ї–µ–і—Б—В–≤–Є–µ: —Б—Г–Љ–Љ–∞ –њ–µ—А–≤—Л—Е
n
{\displaystyle n}
n
{\displaystyle n}
Q
1
+
Q
2
+
Q
3
+
⋯ вЛѓ -->
+
Q
n
=
(
T
n
)
2
{\displaystyle Q_{1}+Q_{2}+Q_{3}+\dots +Q_{n}=(T_{n})^{2}}
–†–∞–Ј–љ–Њ—Б—В—М –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П —Б–Њ—Б–µ–і–љ–Є–Љ–Є –Ї—Г–±–Є—З–µ—Б–Ї–Є–Љ–Є —З–Є—Б–ї–∞–Љ–Є –µ—Б—В—М —Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ–Њ–µ —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ. –°–ї–µ–і—Б—В–≤–Є–µ: —Б—Г–Љ–Љ–∞ –њ–µ—А–≤—Л—Е
n
{\displaystyle n}
Q
n
{\displaystyle Q_{n}}
[ 53]
–Т—Л—А–∞–ґ–µ–љ–Є–µ –Ї—Г–±–Є—З–µ—Б–Ї–Њ–≥–Њ —З–Є—Б–ї–∞ —З–µ—А–µ–Ј —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–µ[ 53]
Q
n
=
Π ќ† -->
n
(
3
)
+
4
Π ќ† -->
n
− вИТ -->
1
(
3
)
+
Π ќ† -->
n
− вИТ -->
2
(
3
)
{\displaystyle Q_{n}=\Pi _{n}^{(3)}+4\Pi _{n-1}^{(3)}+\Pi _{n-2}^{(3)}}
n
>
2
{\displaystyle n>2}
–Ю–і–љ–∞ –Є–Ј ¬Ђ–≥–Є–њ–Њ—В–µ–Ј –Я–Њ–ї–ї–Њ–Ї–∞ ¬ї (1850 –≥–Њ–і): –Ї–∞–ґ–і–Њ–µ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ –њ—А–µ–і—Б—В–∞–≤–Є–Љ–Њ –Ї–∞–Ї —Б—Г–Љ–Љ–∞ –љ–µ –±–Њ–ї–µ–µ –і–µ–≤—П—В–Є –Ї—Г–±–Є—З–µ—Б–Ї–Є—Е —З–Є—Б–µ–ї. –Ф–Њ–Ї–∞–Ј–∞–љ–∞ –≤ –љ–∞—З–∞–ї–µ XX –≤–µ–Ї–∞. –Ю–±—Л—З–љ–Њ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ —Б–µ–Љ–Є –Ї—Г–±–Њ–≤, –љ–Њ 15 —З–Є—Б–µ–ї —В—А–µ–±—Г—О—В –≤–Њ—Б—М–Љ–Є (15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454, –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A018889 –≤ OEIS ), –∞ –і–≤—Г–Љ —З–Є—Б–ї–∞–Љ –љ—Г–ґ–љ—Л –≤—Б–µ –і–µ–≤—П—В—М: 23 –Є 239. –Х—Б–ї–Є, –Ї—А–Њ–Љ–µ —Б–ї–Њ–ґ–µ–љ–Є—П, –і–Њ–њ—Г—Б–Ї–∞—В—М –≤—Л—З–Є—В–∞–љ–Є–µ, —В–Њ –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –Є –њ—П—В–Є –Ї—Г–±–Њ–≤ (–≤–Њ–Ј–Љ–Њ–ґ–љ–Њ, —З—В–Њ –і–∞–ґ–µ —З–µ—В—Л—А—С—Е, –љ–Њ —Н—В–Њ –њ–Њ–Ї–∞ –љ–µ –і–Њ–Ї–∞–Ј–∞–љ–Њ)[ 54]
–Я—А–Њ–Є–Ј–≤–Њ–і—П—Й–∞—П —Д—Г–љ–Ї—Ж–Є—П –Ї—Г–±–Є—З–µ—Б–Ї–Є—Е —З–Є—Б–µ–ї –Є–Љ–µ–µ—В –≤–Є–і[ 53]
f
(
x
)
=
x
(
x
2
+
4
x
+
1
)
(
x
− вИТ -->
1
)
4
{\displaystyle f(x)={\frac {x(x^{2}+4x+1)}{(x-1)^{4}}}}
|
x
|
<
1
{\displaystyle |x|<1}
–Ю–њ–Є—Б–∞–љ–љ—Л–µ –≤—Л—И–µ —В—А—С—Е–Љ–µ—А–љ—Л–µ –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–Є –Љ–Њ–ґ–љ–Њ –Њ–±–Њ–±—Й–Є—В—М –љ–∞ —З–µ—В—Л—А–µ –Є –±–Њ–ї–µ–µ –Є–Ј–Љ–µ—А–µ–љ–Є–є. –Р–љ–∞–ї–Њ–≥–Њ–Љ —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л—Е —З–Є—Б–µ–ї –≤
d
{\displaystyle d}
—Б–Є–Љ–њ–ї–µ–Ї—Б–љ—Л–µ —З–Є—Б–ї–∞¬ї, –љ–∞–Ј—Л–≤–∞–µ–Љ—Л–µ —В–∞–Ї–ґ–µ –≥–Є–њ–µ—А—В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–Љ–Є [ 55]
S
n
[
d
]
=
(
n
− вИТ -->
1
+
d
)
!
(
n
− вИТ -->
1
)
!
d
!
{\displaystyle S_{n}^{[d]}={\frac {(n-1+d)!}{(n-1)!\ d!}}}
–Ш—Е —З–∞—Б—В–љ—Л–Љ —Б–ї—Г—З–∞–µ–Љ –≤—Л—Б—В—Г–њ–∞—О—В:
–Ф—А—Г–≥–Є–µ —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–Є –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е —З–Є—Б–µ–ї вАФ –≥–Є–њ–µ—А–Ї—Г–±–Є—З–µ—Б–Ї–Є–µ :
Q
n
[
d
]
=
n
d
{\displaystyle Q_{n}^{[d]}=n^{d}}
(
d
=
4
)
{\displaystyle (d=4)}
–±–Є–Ї–≤–∞–і—А–∞—В–љ—Л–Љ–Є [ 55]
–Э–µ–Ї–Њ—В–Њ—А—Л–µ —Д–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞ –Љ–Њ–≥—Г—В –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—В—М –±–Њ–ї–µ–µ —З–µ–Љ –Њ–і–љ–Њ–є —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–Є –њ–ї–Њ—Б–Ї–Є—Е –Є/–Є–ї–Є –Љ–љ–Њ–≥–Њ–Љ–µ—А–љ—Л—Е —З–Є—Б–µ–ї, –њ—А–Є–Љ–µ—А—Л –і–ї—П –њ–ї–Њ—Б–Ї–Є—Е —З–Є—Б–µ–ї —Г–ґ–µ –њ—А–Є–≤–Њ–і–Є–ї–Є—Б—М –≤—Л—И–µвЮ§ вЮ§ [ 56]
–Я—П—В—М —З–Є—Б–µ–ї
1
,
10
,
120
,
1540
,
7140
{\displaystyle 1,10,120,1540,7140}
A027568 –≤ OEIS ).
–І–µ—В—Л—А–µ —З–Є—Б–ї–∞
1
,
55
,
91
,
208335
{\displaystyle 1,55,91,208335}
A039596 –≤ OEIS ).
–Ґ—А–Є —З–Є—Б–ї–∞
1
,
4
,
19600
{\displaystyle 1,4,19600}
A003556 –≤ OEIS ).
–Ф–≤–∞ —З–Є—Б–ї–∞
1
,
4900
{\displaystyle 1,4900}
–Ы—О–Ї–∞ ¬ї –Є–ї–Є ¬Ђ–Ј–∞–і–∞—З–∞ –Њ –њ—Г—И–µ—З–љ—Л—Е —П–і—А–∞—Е ¬ї (1875 –≥–Њ–і). –Я–Њ–ї–љ–Њ–µ —А–µ—И–µ–љ–Є–µ –і–∞–ї –≤ 1918 –≥–Њ–і—Г –Ф–ґ–Њ—А–і–ґ –Э–µ–≤–Є–ї–ї –Т–∞—В—Б–Њ–љ [ 57] –Э–Є–Ї–∞–Ї–Њ–µ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–µ —З–Є—Б–ї–Њ, –Ї—А–Њ–Љ–µ 1, –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ[ 58] [ 56]
—В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ –Є –Ї—Г–±–Є—З–µ—Б–Ї–Є–Љ;
—В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ –Є –±–Є–Ї–≤–∞–і—А–∞—В–љ—Л–Љ [ 59]
—В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ –Є –њ—П—В–Њ–є —Б—В–µ–њ–µ–љ—М—О —Ж–µ–ї–Њ–≥–Њ —З–Є—Б–ї–∞[ 58]
—Ж–µ–љ—В—А–Є—А–Њ–≤–∞–љ–љ—Л–Љ —И–µ—Б—В–Є—Г–≥–Њ–ї—М–љ—Л–Љ –Є –Ї—Г–±–Є—З–µ—Б–Ї–Є–Љ. –Т 1988 –≥–Њ–і—Г –§. –С–µ–є–Ї–µ—А—Б –Є –Ф–ґ. –Ґ–Њ–њ –і–Њ–Ї–∞–Ј–∞–ї–Є, —З—В–Њ –љ–Є–Ї–∞–Ї–Њ–µ —З–Є—Б–ї–Њ, –Ї—А–Њ–Љ–µ 1, –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–Љ –Є –Ї–≤–∞–і—А–∞—В–љ—Л–Љ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–Љ[ 60] [ 56]
—В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–µ –Є –Ї—Г–±–Є—З–µ—Б–Ї–Є–µ;
–Ї–≤–∞–і—А–∞—В–љ—Л–µ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–µ –Є –Ї—Г–±–Є—З–µ—Б–Ї–Є–µ;
—В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–µ –Є –±–Є–Ї–≤–∞–і—А–∞—В–љ—Л–µ;
–Ї–≤–∞–і—А–∞—В–љ—Л–µ –њ–Є—А–∞–Љ–Є–і–∞–ї—М–љ—Л–µ –Є –±–Є–Ї–≤–∞–і—А–∞—В–љ—Л–µ.
–Т –∞–љ—В–Є—З–љ—Л–µ –≤—А–µ–Љ–µ–љ–∞, –Ї–Њ–≥–і–∞ –∞—А–Є—Д–Љ–µ—В–Є–Ї–∞ –љ–µ –Њ—В–і–µ–ї—П–ї–∞—Б—М –Њ—В –≥–µ–Њ–Љ–µ—В—А–Є–Є, –њ–Є—Д–∞–≥–Њ—А–µ–є—Ж—Л (VI –≤–µ–Ї –і–Њ –љ. —Н.) —А–∞–Ј–ї–Є—З–∞–ї–Є –µ—Й—С –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –≤–Є–і–Њ–≤ —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї[ 61]
–Ы–Є–љ–µ–є–љ—Л–µ —З–Є—Б–ї–∞ вАФ —З–Є—Б–ї–∞, ¬Ђ–Є–Ј–Љ–µ—А—П–µ–Љ—Л–µ —В–Њ–ї—М–Ї–Њ –µ–і–Є–љ–Є—Ж–µ–є¬ї, —В–Њ –µ—Б—В—М, –≤ —Б–Њ–≤—А–µ–Љ–µ–љ–љ–Њ–є —В–µ—А–Љ–Є–љ–Њ–ї–Њ–≥–Є–Є, –њ—А–Њ—Б—В—Л–µ —З–Є—Б–ї–∞ (—Г –Х–≤–Ї–ї–Є–і–∞ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П —В–µ—А–Љ–Є–љ ¬Ђ–њ–µ—А–≤—Л–µ —З–Є—Б–ї–∞ ¬ї, –і—А.-–≥—А–µ—З. ѕАѕБѕОѕДќњќє ќ±ѕБќєќЄќЉќњќѓ –Я–ї–Њ—Б–Ї–Є–µ (–Є–ї–Є –њ–ї–Њ—Б–Ї–Њ—Б—В–љ—Л–µ) —З–Є—Б–ї–∞ вАФ —З–Є—Б–ї–∞, –њ—А–µ–і—Б—В–∞–≤–Є–Љ—Л–µ –≤ –≤–Є–і–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –і–≤—Г—Е —Б–Њ–Љ–љ–Њ–ґ–Є—В–µ–ї–µ–є, –±–ЊћБ–ї—М—И–Є—Е –µ–і–Є–љ–Є—Ж—Л, —В–Њ –µ—Б—В—М —Б–Њ—Б—В–∞–≤–љ—Л–µ .
–І–∞—Б—В–љ—Л–Љ —Б–ї—Г—З–∞–µ–Љ —П–≤–ї—П—О—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞ (–≤ –Є—Б—В–Њ—З–љ–Є–Ї–∞—Е –Є–љ–Њ–≥–і–∞ –љ–∞–Ј—Л–≤–∞—О—В—Б—П ¬Ђ–њ—А–Њ–і–Њ–ї–≥–Њ–≤–∞—В—Л–Љ–Є ¬ї, –∞–љ–≥–ї. oblong ), –њ—А–µ–і—Б—В–∞–≤–ї—П—О—Й–Є–µ —Б–Њ–±–Њ–є –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –і–≤—Г—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л—Е —Ж–µ–ї—Л—Е —З–Є—Б–µ–ї[ 62]
n
(
n
+
1
)
,
n
⩾ в©Њ -->
0.
{\displaystyle n(n+1),n\geqslant 0.}
–Ґ–µ–ї–µ—Б–љ—Л–µ —З–Є—Б–ї–∞ вАФ —З–Є—Б–ї–∞, –њ—А–µ–і—Б—В–∞–≤–Є–Љ—Л–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ–Љ —В—А—С—Е —Б–Њ–Љ–љ–Њ–ґ–Є—В–µ–ї–µ–є, –±–ЊћБ–ї—М—И–Є—Е –µ–і–Є–љ–Є—Ж—Л.–Ъ–Њ–Љ–Љ–µ–љ—В–∞—В–Њ—А –Х–≤–Ї–ї–Є–і–∞ –Ф. –Ф. –Ь–Њ—А–і—Г—Е–∞–є-–С–Њ–ї—В–Њ–≤—Б–Ї–Њ–є –њ–Њ—П—Б–љ—П–µ—В[ 63]
–Ґ–µ—А–Љ–Є–љ—Л ¬Ђ–њ–ї–Њ—Б–Ї–Њ—Б—В–љ–Њ–µ¬ї –Є ¬Ђ—В–µ–ї–µ—Б–љ–Њ–µ¬ї —З–Є—Б–ї–Њ —П–≤–ї—П—О—В—Б—П, –≤–µ—А–Њ—П—В–љ–Њ, –њ–µ—А–µ–ґ–Є—В–Ї–Њ–Љ –±–Њ–ї–µ–µ —А–∞–љ–љ–µ–≥–Њ –њ–µ—А–Є–Њ–і–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є –Љ—Л—Б–ї–Є, –Ї–Њ–≥–і–∞ —З–Є—Б–ї–Њ –Є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є –Њ–±—А–∞–Ј –±—Л–ї–Є –µ—Й—С —В–µ—Б–љ–µ–µ —Б–≤—П–Ј–∞–љ—Л, –Ї–Њ–≥–і–∞ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ —З–Є—Б–ї–∞
a
{\displaystyle a}
b
{\displaystyle b}
b
{\displaystyle b}
a
{\displaystyle a}
–Т –љ–∞—Б—В–Њ—П—Й–µ–µ –≤—А–µ–Љ—П –њ—А–Њ—Б—В—Л–µ —З–Є—Б–ї–∞ –љ–µ –Њ—В–љ–Њ—Б—П—В –Ї —Д–Є–≥—Г—А–љ—Л–Љ, –∞ —В–µ—А–Љ–Є–љ—Л ¬Ђ–њ–ї–Њ—Б–Ї–Њ–µ —З–Є—Б–ї–Њ¬ї –Є ¬Ђ—В–µ–ї–µ—Б–љ–Њ–µ —З–Є—Б–ї–Њ¬ї –≤—Л—И–ї–Є –Є–Ј —Г–њ–Њ—В—А–µ–±–ї–µ–љ–Є—П[ 63]
–І–Є—Б–ї–∞ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Я–∞—Б–Ї–∞–ї—П –Њ–±–љ–∞—А—Г–ґ–Є–≤–∞—О—В —Б–≤—П–Ј—М —Б–Њ –Љ–љ–Њ–≥–Є–Љ–Є —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В—П–Љ–Є —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї.
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
{\displaystyle {\begin{array}{c}1\\1\quad 1\\1\quad 2\quad 1\\{\color {red}1}\quad 3\quad 3\quad 1\\1\quad {\color {red}4}\quad 6\quad 4\quad 1\\1\quad 5\quad {\color {red}10}\quad 10\quad 5\quad 1\\1\quad 6\quad 15\quad {\color {red}20}\quad 15\quad 6\quad 1\\1\quad 7\quad 21\quad 35\quad {\color {red}35}\quad 21\quad 7\quad 1\\\end{array}}}
–Ґ–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ –Я–∞—Б–Ї–∞–ї—П (–≤—Л–і–µ–ї–µ–љ—Л –Ї—А–∞—Б–љ—Л–Љ)
–Э–∞ —В—А–µ—В—М–µ–є –ї–Є–љ–Є–Є –≤ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ –Я–∞—Б–Ї–∞–ї—П –љ–∞—Е–Њ–і—П—В—Б—П —В—А–µ—Г–≥–Њ–ї—М–љ—Л–µ —З–Є—Б–ї–∞, –∞ –љ–∞ —З–µ—В–≤—С—А—В–Њ–є вАФ —В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞ (—Б–Љ. —А–Є—Б—Г–љ–Њ–Ї). –≠—В–Њ –Њ–±—К—П—Б–љ—П–µ—В—Б—П —В–µ–Љ, —З—В–Њ
n
{\displaystyle n}
n
{\displaystyle n}
–њ–µ–љ—В–∞—В–Њ–њ–љ—Л–µ —З–Є—Б–ї–∞ –Є —В. –і. –Т—Б–µ –Њ–љ–Є, –Ї–∞–Ї –Є –њ—А–Њ—З–Є–µ —З–Є—Б–ї–∞ –≤–љ—Г—В—А–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Я–∞—Б–Ї–∞–ї—П, —П–≤–ї—П—О—В—Б—П –±–Є–љ–Њ–Љ–Є–∞–ї—М–љ—Л–Љ–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є .
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –≤—Б–µ –≤–љ—Г—В—А–µ–љ–љ–Є–µ —Н–ї–µ–Љ–µ–љ—В—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Я–∞—Б–Ї–∞–ї—П —П–≤–ї—П—О—В—Б—П —Д–Є–≥—Г—А–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є, –њ—А–Є—З—С–Љ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л —А–∞–Ј–ї–Є—З–љ—Л–µ –Є—Е —А–∞–Ј–љ–Њ–≤–Є–і–љ–Њ—Б—В–Є. –Т–і–Њ–ї—М –Ї–∞–ґ–і–Њ–є —Б—В—А–Њ–Ї–Є, —Б–ї–µ–≤–∞ –љ–∞–њ—А–∞–≤–Њ, –Є–і—Г—В –≥–Є–њ–µ—А—В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –≤–Њ–Ј—А–∞—Б—В–∞—О—Й–µ–є —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ —Б—Г–Љ–Љ–∞ –≤—Б–µ—Е —З–Є—Б–µ–ї
n
{\displaystyle n}
2
n
,
{\displaystyle 2^{n},}
n
{\displaystyle n}
—З–Є—Б–ї—Г –Ь–µ—А—Б–µ–љ–љ–∞
M
n
.
{\displaystyle M_{n}.}
[ 64]
–Ь–љ–Њ–≥–Є–µ —В–µ–Њ—А–µ–Љ—Л —В–µ–Њ—А–Є–Є —З–Є—Б–µ–ї –і–Њ–њ—Г—Б–Ї–∞—О—В —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–Ї—Г –≤ —В–µ—А–Љ–Є–љ–∞—Е —Д–Є–≥—Г—А–љ—Л—Е —З–Є—Б–µ–ї. –Э–∞–њ—А–Є–Љ–µ—А, –≥–Є–њ–Њ—В–µ–Ј–∞ –Ъ–∞—В–∞–ї–∞–љ–∞ —Г—В–≤–µ—А–ґ–і–∞–µ—В, —З—В–Њ —Б—А–µ–і–Є –≥–Є–њ–µ—А–Ї—Г–±–Є—З–µ—Б–Ї–Є—Е —З–Є—Б–µ–ї –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ—Л—Е —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–µ–є —В–Њ–ї—М–Ї–Њ –Њ–і–љ–∞ –њ–∞—А–∞ –Њ—В–ї–Є—З–∞–µ—В—Б—П –љ–∞ 1:
3
2
=
2
3
+
1
{\displaystyle 3^{2}=2^{3}+1}
[ 65]
–Т—Б—П–Ї–Њ–µ —З—С—В–љ–Њ–µ —Б–Њ–≤–µ—А—И–µ–љ–љ–Њ–µ —З–Є—Б–ї–Њ —П–≤–ї—П–µ—В—Б—П —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ[ 66] [ 67]
–У–Є–њ–Њ—В–µ–Ј–∞ –Ы–µ–ґ–∞–љ–і—А–∞ (1808 –≥–Њ–і, –Њ–љ–∞ –ґ–µ —В—А–µ—В—М—П –њ—А–Њ–±–ї–µ–Љ–∞ –≠–і–Љ—Г–љ–і–∞ –Ы–∞–љ–і–∞—Г ): –Љ–µ–ґ–і—Г –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л–Љ–Є –Ї–≤–∞–і—А–∞—В–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є –≤—Б–µ–≥–і–∞ –љ–∞–є–і—С—В—Б—П –њ—А–Њ—Б—В–Њ–µ —З–Є—Б–ї–Њ . –Ф–Њ —Б–Є—Е –њ–Њ—А –љ–µ –і–Њ–Ї–∞–Ј–∞–љ–∞.
–°—Г–Љ–Љ–∞ –њ–µ—А–≤—Л—Е
n
{\displaystyle n}
(
n
>
2
)
{\displaystyle (n>2)}
–Љ–∞–≥–Є—З–µ—Б–Ї–Њ–≥–Њ –Ї–≤–∞–і—А–∞—В–∞ —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В–Є
n
× √Ч -->
n
{\displaystyle n\times n}
T
n
2
n
{\displaystyle {\frac {T_{n^{2}}}{n}}}
T
n
− вИТ -->
1
{\displaystyle T_{n-1}}
T
n
{\displaystyle T_{n}}
[ 68]
–І–Є—Б–ї–Њ –Ь–µ—А—Б–µ–љ–љ–∞ , –±–Њ–ї—М—И–µ–µ 1, –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Ї–≤–∞–і—А–∞—В–љ—Л–Љ, –Ї—Г–±–Є—З–µ—Б–Ї–Є–Љ –Є–ї–Є –Є–љ—Л–Љ –≥–Є–њ–µ—А–Ї—Г–±–Є—З–µ—Б–Ї–Є–Љ, –љ–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ. –Ґ—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–µ–ї –Ь–µ—А—Б–µ–љ–љ–∞ –≤—Б–µ–≥–Њ —З–µ—В—Л—А–µ:
1
,
3
,
15
,
4095
{\displaystyle 1,3,15,4095}
—Г—А–∞–≤–љ–µ–љ–Є—П –†–∞–Љ–∞–љ—Г–і–ґ–∞–љ–∞ вАФ –Э–∞–≥–µ–ї—П :
2
n
− вИТ -->
7
=
x
2
{\displaystyle 2^{n}-7=x^{2}}
n
=
3
,
4
,
5
,
7
,
15
{\displaystyle n=3,4,5,7,15}
A060728 –≤ OEIS ), –Є –њ—А–Є
n
>
3
{\displaystyle n>3}
M
n
− вИТ -->
3
{\displaystyle M_{n-3}}
[ 64]
–Я–Њ–ї—Г—З–µ–љ–Є–µ —З–Є—Б–µ–ї –§–Є–±–Њ–љ–∞—З—З–Є –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Я–∞—Б–Ї–∞–ї—П –І–Є—Б–ї–Њ –§–µ—А–Љ–∞ —В–∞–Ї–ґ–µ –љ–µ –Љ–Њ–ґ–µ—В –±—Л—В—М –Ї–≤–∞–і—А–∞—В–љ—Л–Љ, –Ї—Г–±–Є—З–µ—Б–Ї–Є–Љ –Є–ї–Є –Є–љ—Л–Љ –≥–Є–њ–µ—А–Ї—Г–±–Є—З–µ—Б–Ї–Є–Љ, –љ–Њ –≤ –µ–і–Є–љ—Б—В–≤–µ–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ –Љ–Њ–ґ–µ—В –±—Л—В—М —В—А–µ—Г–≥–Њ–ї—М–љ—Л–Љ:
F
0
=
3
{\displaystyle F_{0}=3}
[ 64]
–°—А–µ–і–Є —З–Є—Б–µ–ї –§–Є–±–Њ–љ–∞—З—З–Є –Є–Љ–µ—О—В—Б—П —В–Њ–ї—М–Ї–Њ —В—А–Є –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–ї–∞ (0, 1 –Є 144) –Є —З–µ—В—Л—А–µ —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е (1, 3, 21, 55, –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М A039595 –≤ OEIS ). –Х—Б–ї–Є –њ–Њ–≤–µ—А–љ—Г—В—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –Я–∞—Б–Ї–∞–ї—П, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ, —В–Њ —З–Є—Б–ї–∞ –§–Є–±–Њ–љ–∞—З—З–Є –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –Ї–∞–Ї —Б—Г–Љ–Љ—Л –≤–і–Њ–ї—М –≤–Њ—Б—Е–Њ–і—П—Й–Є—Е –і–Є–∞–≥–Њ–љ–∞–ї–µ–є; —Н—В–Њ—В —Д–∞–Ї—В –і–∞—С—В —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ —З–Є—Б–ї–∞ –§–Є–±–Њ–љ–∞—З—З–Є –њ–Њ –≥–Є–њ–µ—А—В–µ—В—А–∞—Н–і—А–∞–ї—М–љ—Л–Љ —З–Є—Б–ї–∞–Љ[ 69]
–°—А–µ–і–Є —З–Є—Б–µ–ї –Ы—О–Ї–∞ –Ї–≤–∞–і—А–∞—В–љ—Л—Е —З–Є—Б–µ–ї –і–≤–∞ (1 –Є 4), –∞ —В—А–µ—Г–≥–Њ–ї—М–љ—Л—Е —В—А–Є (1, 3, 5778)[ 69]
–І–Є—Б–ї–∞ –Ъ–∞—В–∞–ї–∞–љ–∞
C
a
t
n
{\displaystyle Cat_{n}}
[ 70]
C
a
t
n
=
S
n
+
1
[
n
]
− вИТ -->
S
n
+
2
[
n
− вИТ -->
1
]
{\displaystyle Cat_{n}=S_{n+1}^{[n]}-S_{n+2}^{[n-1]}}
–Х—Й—С –Њ–і–Є–љ –Ї–ї–∞—Б—Б —З–Є—Б–µ–ї, —В–µ—Б–љ–Њ —Б–≤—П–Ј–∞–љ–љ—Л—Е —Б —Д–Є–≥—Г—А–љ—Л–Љ–Є вАФ —З–Є—Б–ї–∞ –°—В–Є—А–ї–Є–љ–≥–∞ –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞
S
(
n
,
m
)
{\displaystyle S(n,m)}
T
n
=
S
(
n
+
1
,
n
)
{\displaystyle T_{n}=S(n+1,n)}
S
(
n
,
2
)
+
1
{\displaystyle S(n,2)+1}
n
{\displaystyle n}
Q
2
[
n
]
{\displaystyle Q_{2}^{[n]}}
n
{\displaystyle n}
S
(
n
,
m
)
{\displaystyle S(n,m)}
[ 70]
Q
n
[
d
]
=
∑ вИС -->
m
=
0
d
S
(
d
,
m
)
n
(
n
− вИТ -->
1
)
… вА¶ -->
(
n
− вИТ -->
m
+
1
)
{\displaystyle Q_{n}^{[d]}=\sum _{m=0}^{d}{S(d,m)n(n-1)\dots (n-m+1)}}
вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 9.вЖС –Ш—Б—В–Њ—А–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є. –° –і—А–µ–≤–љ–µ–є—И–Є—Е –≤—А–µ–Љ–µ–љ –і–Њ –љ–∞—З–∞–ї–∞ –Э–Њ–≤–Њ–≥–Њ –≤—А–µ–Љ–µ–љ–Є // –Ш—Б—В–Њ—А–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є / –Я–Њ–і —А–µ–і–∞–Ї—Ж–Є–µ–є –Р. –Я. –Ѓ—И–Ї–µ–≤–Є—З–∞ , –≤ —В—А—С—Е —В–Њ–Љ–∞—Е. вАФ –Ь. : –Э–∞—Г–Ї–∞, 1970. вАФ –Ґ. I. вАФ –°. 68. вАФ 352 —Б.вЖС –§–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞ // –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є —Н–љ—Ж–Є–Ї–ї–Њ–њ–µ–і–Є—З–µ—Б–Ї–Є–є —Б–ї–Њ–≤–∞—А—М . вАФ –Ь. : –°–Њ–≤–µ—В—Б–Ї–∞—П —Н–љ—Ж–Є–Ї–ї–Њ–њ–µ–і–Є—П, 1988. вАФ –°. 607 . вАФ 847 —Б.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 10.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 12вАФ13.вЖС –Ю–ґ–Є–≥–Њ–≤–∞ –Х. –Я. –І—В–Њ —В–∞–Ї–Њ–µ —В–µ–Њ—А–Є—П —З–Є—Б–µ–ї. вАФ –Ь. : –Ч–љ–∞–љ–Є–µ, 1970. вАФ –°. 56вАФ57.вЖС –Р—А–Є—Д–Љ–µ—В–Є—З–µ—Б–Ї–Є–є —А—П–і // –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—П —Н–љ—Ж–Є–Ї–ї–Њ–њ–µ–і–Є—П (–≤ 5 —В–Њ–Љ–∞—Е) . вАФ –Ь. : –°–Њ–≤–µ—В—Б–Ї–∞—П –≠–љ—Ж–Є–Ї–ї–Њ–њ–µ–і–Є—П , 1982. вАФ –Ґ. 1. –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ 13 –љ–Њ—П–±—А—П 2013 –≥–Њ–і–∞.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 15.вЖС –Ч–∞ —Б—В—А–∞–љ–Є—Ж–∞–Љ–Є —Г—З–µ–±–љ–Є–Ї–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є, 1996 , —Б. 50.вЖС 1 2 3 4 5 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 217.вЖС Sameen Ahmed Khan. Sums of the powers ofreciprocals of polygonal numbers (—Д–Њ—А–Љ—Г–ї–∞ 23)вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 14.вЖС –Ф–Є–Њ—Д–∞–љ—В –Р–ї–µ–Ї—Б–∞–љ–і—А–Є–є—Б–Ї–Є–є .–Р—А–Є—Д–Љ–µ—В–Є–Ї–∞ –Є –Ъ–љ–Є–≥–∞ –Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ—Л—Е —З–Є—Б–ї–∞—Е / –Я–µ—А. –Ш. –Э. –Т–µ—Б–µ–ї–Њ–≤—Б–Ї–Њ–≥–Њ; –†–µ–і. –Є –Ї–Њ–Љ–Љ–µ–љ—В. –Ш. –У. –С–∞—И–Љ–∞–Ї–Њ–≤–Њ–є. вАФ –Ь. : –Э–∞—Г–Ї–∞, 1974. вАФ –°. 48. вАФ 328 —Б. –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ 24 –∞–њ—А–µ–ї—П 2007 –≥–Њ–і–∞.вЖС 1 2 –Ь–∞—В–≤–Є–µ–≤—Б–Ї–∞—П –У. –Я. –£—З–µ–љ–Є–µ –Њ —З–Є—Б–ї–µ –љ–∞ —Б—А–µ–і–љ–µ–≤–µ–Ї–Њ–≤–Њ–Љ –С–ї–Є–ґ–љ–µ–Љ –Є –°—А–µ–і–љ–µ–Љ –Т–Њ—Б—В–Њ–Ї–µ. вАФ –Ґ–∞—И–Ї–µ–љ—В: –§–Р–Э, 1967. вАФ –°. 22вАФ23. вАФ 344 —Б.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 237.вЖС –Т–Є–ї–µ–љ–Ї–Є–љ –Э. –ѓ. –Я–Њ–њ—Г–ї—П—А–љ–∞—П –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–∞ . вАФ –Ь. : –Э–∞—Г–Ї–∞, 1975. вАФ –°. 10вАФ11. вАФ 208 —Б. –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ 5 –Є—О–љ—П 2016 –≥–Њ–і–∞.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 10.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 19вАФ24.вЖС Dickson, 2005 , p. 27.вЖС Weisstein, Eric W. Telescoping Sum (–∞–љ–≥–ї.) –љ–∞ —Б–∞–є—В–µ Wolfram MathWorld .вЖС Dickson, 2005 , p. 3.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 225.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 19.вЖС 1 2 Dickson, 2005 , p. 2.вЖС –Э–µ–Ї–Њ—В–Њ—А—Л–µ –Ї–Њ–љ–µ—З–љ—Л–µ —З–Є—Б–ї–Њ–≤—Л–µ —А—П–і—Л (—А—Г—Б.) . Math24.ru . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 14 –Є—О–љ—П 2019. –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ 14 –Є—О–љ—П 2019 –≥–Њ–і–∞.вЖС –Ъ–Њ—Е–∞—Б—М –Ъ. –Я. –°—Г–Љ–Љ–∞ –Њ–±—А–∞—В–љ—Л—Е –Ї–≤–∞–і—А–∞—В–Њ–≤ // –Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –њ—А–Њ—Б–≤–µ—Й–µ–љ–Є–µ. вАФ 2004. вАФ –Т—Л–њ. 8 . вАФ –°. 142вАФ163 .вЖС –Т–∞–є–љ—И—В–µ–є–љ –§. –Т. –†–∞–Ј–±–Є–µ–љ–Є–µ —З–Є—Б–µ–ї. : [–∞—А—Е. 9 –∞–≤–≥—Г—Б—В–∞ 2019вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 22.вЖС 1 2 3 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 37вАФ38.вЖС –Т —Б–∞–Љ–Њ–Љ –і–µ–ї–µ, –њ—Г—Б—В—М
a
n
1
+
b
n
2
{\displaystyle {\frac {a}{n_{1}}}+{\frac {b}{n_{2}}}}
K
{\displaystyle K}
n
1
{\displaystyle n_{1}}
n
2
{\displaystyle n_{2}}
n
1
{\displaystyle n_{1}}
b
n
1
n
2
=
K
n
1
− вИТ -->
a
{\displaystyle {\frac {bn_{1}}{n_{2}}}=Kn_{1}-a}
n
2
{\displaystyle n_{2}}
b
n
1
{\displaystyle bn_{1}}
–Њ–±–Њ–±—Й—С–љ–љ–Њ–є –ї–µ–Љ–Љ–µ –Х–≤–Ї–ї–Є–і–∞ ,
n
2
{\displaystyle n_{2}}
b
{\displaystyle b}
вЖС 1 2 3 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 38вАФ39.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 17вАФ19.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 33.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 34вАФ37.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 25вАФ34.вЖС Lawrence Downey, Boon W. Ong . Beyond the Basel Problem: Sums ofReciprocals of Figurate Numbers –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 29 –і–µ–Ї–∞–±—А—П 2019 –љ–∞ Wayback Machine вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 39вАФ40.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 40вАФ41.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 42.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 43.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 44вАФ46.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 45вАФ46.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 46.вЖС Dickson, 2005 , p. 23.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 48.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 70вАФ71.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 76.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 74вАФ75.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 239.вЖС Frederick Pollock. On the extension of the principle of Fermat's theorem on the polygonal numbers to the higher order of series whose ultimate differences are constant. With a new theorem proposed, applicable to all the orders (–∞–љ–≥–ї.) // Abstracts of the Papers Communicated to the Royal Society of London : journal. вАФ 1850. вАФ Vol. 5 . вАФ P. 922вАФ924 . вАФ JSTOR 111069 вЖС Robitaille, David F. Mathematics and chess // The Arithmetic Teacher. вАФ 1974. вАФ Vol. 21, no. 5 (–Љ–∞–є). вАФ P. 396вАФ400. вАФ JSTOR 41190919 вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 75.вЖС 1 2 3 4 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 78вАФ81.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 231вАФ232.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 126вАФ134.вЖС 1 2 3 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 77вАФ78.вЖС Watson G. N. The Problem of the Square Pyramid // Messenger. Math. 1918. Vol. 48. P. 1-16.вЖС 1 2 The Penguin Dictionary of Curious and Interesting Numbers (–∞–љ–≥–ї.) . –Ф–∞—В–∞ –Њ–±—А–∞—Й–µ–љ–Є—П: 9 –Љ–∞—А—В–∞ 2021.вЖС Dickson, 2005 , p. 8.вЖС Beukers F., Top J. On oranges and integral points on certain plane cubic curves // Nieuw Archief voor Wiskunde (4). вАФ 1988. вАФ Vol. 6, no. 3. вАФ P. 203вАФ210.вЖС –У–∞–є–і–µ–љ–Ї–Њ –Я. –Я. –≠–≤–Њ–ї—О—Ж–Є—П –њ–Њ–љ—П—В–Є—П –љ–∞—Г–Ї–Є (—Б—В–∞–љ–Њ–≤–ї–µ–љ–Є–µ –Є —А–∞–Ј–≤–Є—В–Є–µ –њ–µ—А–≤—Л—Е –љ–∞—Г—З–љ—Л—Е –њ—А–Њ–≥—А–∞–Љ–Љ) –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 19 –∞–≤–≥—Г—Б—В–∞ 2014 –љ–∞ Wayback Machine , –≥–ї–∞–≤–∞ 1. –Ь.: –Э–∞—Г–Ї–∞, 1980.вЖС Ben-Menahem, Ari. Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1 : [–∞—А—Е. 11 –љ–Њ—П–±—А—П 2021ISBN 9783540688310 .вЖС 1 2 –Э–∞—З–∞–ї–∞ –Х–≤–Ї–ї–Є–і–∞ / –Я–µ—А–µ–≤–Њ–і —Б –≥—А–µ—З–µ—Б–Ї–Њ–≥–Њ –Є –Ї–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є –Ф. –Ф. –Ь–Њ—А–і—Г—Е–∞–є-–С–Њ–ї—В–Њ–≤—Б–Ї–Њ–≥–Њ –њ—А–Є —А–µ–і–∞–Ї—Ж–Є–Њ–љ–љ–Њ–Љ —Г—З–∞—Б—В–Є–Є –Ь. –ѓ. –Т—Л–≥–Њ–і—Б–Ї–Њ–≥–Њ –Є –Ш. –Э. –Т–µ—Б–µ–ї–Њ–≤—Б–Ї–Њ–≥–Њ. вАФ –Ь. вАФ–Ы. : –У–Ґ–Ґ–Ш, 1948. вАФ –Ґ. 2. вАФ –°. 10, 268вАФ270. вАФ (–Ъ–ї–∞—Б—Б–Є–Ї–Є –µ—Б—В–µ—Б—В–≤–Њ–Ј–љ–∞–љ–Є—П). вЖС 1 2 3 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 203вАФ205.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 196вАФ197.вЖС –Ч–∞ —Б—В—А–∞–љ–Є—Ж–∞–Љ–Є —Г—З–µ–±–љ–Є–Ї–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є, 1996 , —Б. 51.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 200вАФ201.вЖС –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 222вАФ223.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 208.вЖС 1 2 –Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь., 2016 , —Б. 214вАФ215.
–Т–Є–ї–µ–љ–Ї–Є–љ –Э. –ѓ., –®–Є–±–∞—Б–Њ–≤ –Ы. –Я. –®–Є–±–∞—Б–Њ–≤–∞ 3. –§. –Ч–∞ —Б—В—А–∞–љ–Є—Ж–∞–Љ–Є —Г—З–µ–±–љ–Є–Ї–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є: –Р—А–Є—Д–Љ–µ—В–Є–Ї–∞. –Р–ї–≥–µ–±—А–∞. –У–µ–Њ–Љ–µ—В—А–Є—П . вАФ –Ь. : –Я—А–Њ—Б–≤–µ—Й–µ–љ–Є–µ, 1996. вАФ –°. 48 вАФ52. вАФ 320 —Б. вАФ ISBN 5-09-006575-6 .–У–ї–µ–є–Ј–µ—А –У. –Ш. –Ь. : –Я—А–Њ—Б–≤–µ—Й–µ–љ–Є–µ, 1964. вАФ –°. 84вАФ86. вАФ 376 —Б.–Ф–µ–Ј–∞ –Х. –°–њ–µ—Ж–Є–∞–ї—М–љ—Л–µ —З–Є—Б–ї–∞ –љ–∞—В—Г—А–∞–ї—М–љ–Њ–≥–Њ —А—П–і–∞: –£—З–µ–±–љ–Њ–µ –њ–Њ—Б–Њ–±–Є–µ.. вАФ –Ь. : –Ъ–љ–Є–ґ–љ—Л–є –і–Њ–Љ ¬Ђ–Ы–Ш–С–†–Ю–Ъ–Ю–Ь¬ї, 2011. вАФ 240 —Б. вАФ ISBN 978-5-397-01750-3 .–Ф–µ–Ј–∞ –Х., –Ф–µ–Ј–∞ –Ь. –§–Є–≥—Г—А–љ—Л–µ —З–Є—Б–ї–∞. вАФ –Ь. : –Ь–¶–Э–Ь–Ю, 2016. вАФ 349 —Б. вАФ ISBN 978-5-4439-2400-7 .–Ф–µ–њ–Љ–∞–љ –Ш. –ѓ. –Ш—Б—В–Њ—А–Є—П –∞—А–Є—Д–Љ–µ—В–Є–Ї–Є. –Я–Њ—Б–Њ–±–Є–µ –і–ї—П —Г—З–Є—В–µ–ї–µ–є . вАФ –Ш–Ј–і. –≤—В–Њ—А–Њ–µ. вАФ –Ь. : –Я—А–Њ—Б–≤–µ—Й–µ–љ–Є–µ, 1965. вАФ –°. 150вАФ155.–Ь–∞—В–≤–Є–µ–≤—Б–Ї–∞—П –У. –Я. –Ш—Б—В–Њ—А–Є–Ї–Њ-–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П . вАФ –Ь. : –Э–∞—Г–Ї–∞ , 1983. вАФ вДЦ 27 . вАФ –°. 27вАФ49 .–°–µ—А–њ–Є–љ—Б–Ї–Є–є –Т. –Ь. : –£—З–њ–µ–і–≥–Є–Ј, 1959. вАФ 111 —Б.–°—В–Є–ї–ї–≤–µ–ї–ї –Ф. –У–ї–∞–≤–∞ 3. –У—А–µ—З–µ—Б–Ї–∞—П —В–µ–Њ—А–Є—П —З–Є—Б–µ–ї // –Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞ –Є –µ—С –Є—Б—В–Њ—А–Є—П. вАФ –Ь–Њ—Б–Ї–≤–∞-–Ш–ґ–µ–≤—Б–Ї: –Ш–љ—Б—В–Є—В—Г—В –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л—Е –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є, 2004.Dickson L. E. History of the Theory of Numbers . вАФ New York : Dover, 2005. вАФ Vol. 2: Diophantine Analysis. вАФ P. 22вАФ23.
–°—Б—Л–ї–Ї–Є –љ–∞ –≤–љ–µ—И–љ–Є–µ —А–µ—Б—Г—А—Б—Л
–Ґ–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ —Б–∞–є—В—Л
–°–ї–Њ–≤–∞—А–Є –Є —Н–љ—Ж–Є–Ї–ї–Њ–њ–µ–і–Є–Є –Т –±–Є–±–ї–Є–Њ–≥—А–∞—Д–Є—З–µ—Б–Ї–Є—Е –Ї–∞—В–∞–ї–Њ–≥–∞—Е








































































































































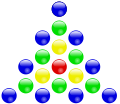
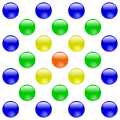
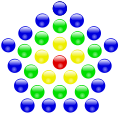
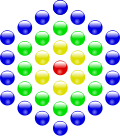































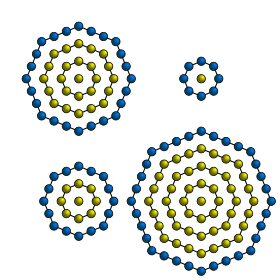




























































![{\displaystyle S_{n}^{[d]}={\frac {(n-1+d)!}{(n-1)!\ d!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28a47962c7f0baec91883adc82aeda56e4695839)
![{\displaystyle S_{n}^{[2]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75baa5e8e4f48950b9f95e7ea0835c86332aead5)
![{\displaystyle S_{n}^{[3]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f84359e60c6739fcab45e20313d1a9c15fb08fd1)
![{\displaystyle S_{n}^{[4]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d44ef89cadef001a85fd17138679ec391a436e2d)
![{\displaystyle Q_{n}^{[d]}=n^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/994da48a0b29edfff10ede51a2387ff370b62a11)























![{\displaystyle Cat_{n}=S_{n+1}^{[n]}-S_{n+2}^{[n-1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e303a9fc2b2d32f4a8e53599babb6e2ada6ef0e9)



![{\displaystyle Q_{2}^{[n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8afaed0172274299d068445d247c03a3c1c16c9a)
![{\displaystyle Q_{n}^{[d]}=\sum _{m=0}^{d}{S(d,m)n(n-1)\dots (n-m+1)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d9f9637833e09aa2d6a5d27d278891ea9a0ee9)






