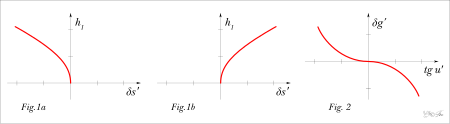
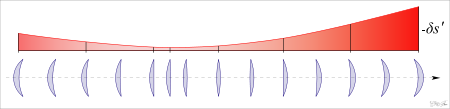
Сферическая аберрация
|
Read other articles:

Restaurant chain in the U.S. state of Washington Bok a BokExterior of the restaurant on Capitol Hill, Seattle, 2022Restaurant informationStateWashingtonCountryUnited States Bok a Bok Fried Chicken, or simply Bok a Bok, is a restaurant chain in the U.S. state of Washington.[1][2] The business specializes in Korean-style fried chicken; the menu has also included chicken sandwiches (including one with yuzu aioli and charred chiles), kimchi mac and cheese, and tots with Chile salt...

Легка атлетика на Літній універсіаді 2013 Дисципліни на доріжці стадіону 100 метрів чоловіки жінки 200 метрів чоловіки жінки 400 метрів чоловіки жінки 800 метрів чоловіки жінки 1500 метрів чоловіки жінки 5000 метрів чоловіки жінки 10 000 метрів чоловіки жінки 100 метрів з бар'єрами жі

اضغط هنا للاطلاع على كيفية قراءة التصنيف ببغاء أنواع مختلفة من الببغاوات. المرتبة التصنيفية رتبة[1][2] التصنيف العلمي فوق النطاق حيويات مملكة عليا حقيقيات النوى مملكة حيوان عويلم ثنائيات التناظر مملكة فرعية ثانويات الفم شعبة حبليات شعيبة&...

القتل خارج نطاق القضاء (ويُسمى أيضًا الإعدام خارج نطاق القضاء) هو قتل شخص على أيدي سلطات حكومية أو أفراد دون موافقة قضائية مسبقة أو إجراء قانوني. تعتبر الإنسانية العقوبةَ خارج عن نطاق القانون عملًا غير أخلاقي غالبًا، لأنها تتجاوز قانون ضمان الحقوق الذي تكفله الولاية التي تح
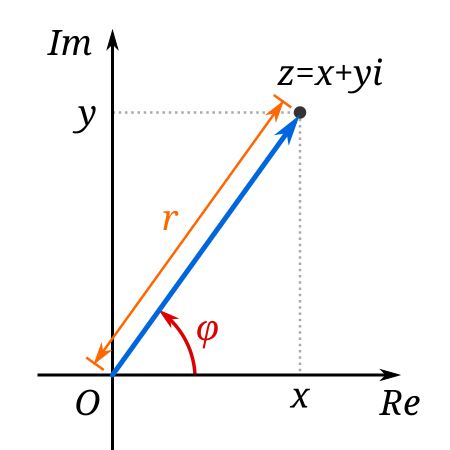
Un número complejo puede ser visualmente representado como un punto localizado en el plano complejo. El valor del ángulo φ {\displaystyle \varphi } es el argumento del número complejo z = x + i y {\displaystyle z=~x~+~iy} . El argumento, abreviado como «arg», de un número complejo z {\displaystyle z} es el ángulo comprendido entre el eje real positivo del plano complejo y la línea que une z {\displaystyle z} con el origen de dicho plano. Definición Geomét...

Religion including traditional Iroquois beliefs and Christian elements Onondaga longhouse on the Six Nations Reservation in the early 1900s The Longhouse Religion is the popular name of the religious movement also known as The Code of Handsome Lake or Gaihwi:io/Kaliwihyo (Good Message), founded in 1799 by the Seneca prophet Handsome Lake (Sganyodaiyoˀ). This movement combines and reinterprets elements of traditional Iroquois religious beliefs with elements adopted from Christianity, primaril...

Hampshire County Cricket Club was formed in 1864, and first appeared in the County Championship in 1895. They played their first List A match in the 1963 Gillette Cup against Derbyshire. The players in this list have all played at least one List A match for Hampshire. Hampshire cricketers who have not represented the county in List A cricket are excluded from the list. Hampshire play their matches at the Rose Bowl (also known as the Ageas Bowl) Players are listed in order of appearance, where...

2012 studio album by Hey! Say! JUMPJUMP WorldStudio album by Hey! Say! JUMPReleasedJune 6, 2012 (Japan)Recorded2012GenreJ-popLabelJ Storm, Johnny & AssociatesProducerJulie K.Hey! Say! JUMP chronology JUMP No. 1(2010) JUMP World(2012) S3ART(2014) Singles from JUMP World Arigatō (Sekai no Doko ni Itemo)Released: December 15, 2010 OVERReleased: May 29, 2011 Magic PowerReleased: September 21, 2011 SUPER DELICATEReleased: February 22, 2012 JUMP World is the second studio album by Hey!...

Michael Jürgs, 2011 Michael Jürgs (* 4. Mai 1945 in Ellwangen; † 4. Juli 2019 in Hamburg) war ein deutscher Journalist und Buchautor. Inhaltsverzeichnis 1 Leben 2 Ehrungen 3 Bibliografie (Auswahl) 4 Literatur 5 Weblinks 6 Einzelnachweise Leben Jürgs studierte Politikwissenschaft, Geschichte und Germanistik in München, brach das Studium jedoch ab und volontierte stattdessen bei der Münchner Abendzeitung, für die er schon während seines Studiums schrieb. Mit 23 Jahren wurde er Che...

此條目需要补充更多来源。 (2014年6月7日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:可移植操作系统接口 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 可移植操作系统接口 (IEEE 1003)状态Published开始年1988最新版本IEEE Std 100...

View that medical treatment is futile This article is about pessimism regarding therapy. For other uses, see Nihilism (disambiguation). Some of this article's listed sources may not be reliable. Please help this article by looking for better, more reliable sources. Unreliable citations may be challenged or deleted. (December 2021) (Learn how and when to remove this template message) In the 19th century, there was a lack of confidence in the remedies of the day. Oliver Wendell Holmes said, ......

Historical fiction novel by Leslie Feinberg Stone Butch Blues Front cover of 2004 Alyson Books paperback editionAuthorLeslie FeinbergCountryUnited StatesLanguageEnglishGenrehistorical fictionPublisherFirebrand BooksPublication dateMarch 1993Media typePrint (hardcover and paperback)ISBN1-56341-030-3OCLC27336208Dewey Decimal813/.54 20LC ClassPS3556.E427 S7 1993 Stone Butch Blues is a historical fiction novel written by Leslie Feinberg about life as a butch lesbian in 1970s America. Wh...

『サムソンとデリラ』ドイツ語: Samson und Delilah英語: Samson and Delilah作者レンブラント・ファン・レイン製作年1629-1630年素材板上に油彩寸法61.3 cm × 61.4 cm (24.1 in × 24.2 in)所蔵絵画館 (ベルリン) 『サムソンとデリラ』(独: Samson und Delilah、英: Samson and Delilah)は、17世紀オランダ黄金時代の巨匠レンブラント・ファン・レインが1629-1630年に�...

Infinite discographyStudio albums6Live albums2Compilation albums2Video albums17Music videos47EPs6Singles29Soundtrack albums4Single albums2 South Korean boy group Infinite has released six studio albums, two compilation albums, two live albums, two reissues, six extended plays, two single albums, and twenty-nine singles. The group debuted in South Korea in June 2010 with the mini album First Invasion and in Japan in November 2011 with a Japanese version of the song BTD (Before the Dawn) releas...

Escudo de Cataluña InformaciónTerritorio CataluñaDescripciónCorona Corona real cerrada[editar datos en Wikidata] El escudo de Cataluña es el símbolo heráldico de la comunidad autónoma catalana, en España, cuyo origen está en las armas hereditarias de los monarcas de la Corona de Aragón. Su derivado, la señera de Cataluña es un símbolo oficializado por la Generalidad de Cataluña incluido en el Estatuto de Autonomía de Cataluña. El escudo, sin embargo, no está regula...

El incidente fronterizo militar entre fuerzas peruanas y ecuatorianas fue un choque armado ocurrido en enero de 1978 en la frontera de ambo países, originados por el avance de un destacamento ecuatoriano en territorio peruano. Incidente fronterizo Perú Ecuador 1978 Parte de Conflicto limítrofe entre el Perú y el Ecuador Mapa donde demuestra el choque armado.Fecha 12 al 20 de enero de 1978Lugar Sub sector del Alto Cenepa - Cordillera del CóndorResultado Victoria del Perú.[1]Consec...

Municipality and town in Valencian Community, SpainBorriolMunicipality and townBorriol Castle FlagSealBorriolLocation of Borriol in the Province of CastellónShow map of Province of CastellónBorriolLocation of Borriol in the Valencian CommunityShow map of Valencian CommunityBorriolLocation of Borriol in SpainShow map of SpainCoordinates: 40°2′32″N 0°4′17″W / 40.04222°N 0.07139°W / 40.04222; -0.07139Country SpainAutonomous community Valencian Comm...

AnalisaMembangkitkan Partisipasi Rakyat dalam PembangunanTipeSurat kabar harianFormatLembar lebarPendiriHarta SusantoSupandi KusumaSoffyanPenerbitYayasan Sikap Press (1972–2007)PT Media Warta Kencana(2007–sekarang)Pemimpin redaksiWar Djamilsejak Agustus 2023Diterbitkan23 Maret 1972; 51 tahun lalu (1972-03-23)BahasaBahasa IndonesiaPusatJl. Jend. A. Yani No. 35–49, Medan, Sumatera Utara 20111Sirkulasi surat kabar35.000 (2015)[1]Pembaca160.000 (2022)[2]Situs webanalisa...

1985 children's fantasy novel by Eiko Kadono This article is about the novels. For other uses, see Kiki's Delivery Service (disambiguation). Majo no TakkyūbinKiki's Delivery Service Japanese book coverAuthorEiko KadonoOriginal title魔女の宅急便Majo no TakkyūbinTranslatorLynne E. Riggs (first edition) Emily Balistrieri (second edition)IllustratorAkiko HayashiCover artistAkiko HayashiCountryJapanLanguageJapaneseSeriesMajo no TakkyūbinGenreChildren's, Fantasy novelPublisherFuk...

2020 filmKill PinochetTheatrical release posterSpanishMatar a Pinochet Directed byJuan Ignacio SabatiniWritten byJuan Ignacio SabatiniEnrique VidelaPablo ParedesStarring Daniela Ramírez Cristián Carvajal Juan Martín Gravina Gastón Salgado Julieta Zylberberg Gabriel Cañas Mario Horton Luis Gnecco Alejandro Goic Productioncompanies Villano DDRio Estudio Leyenda Cine Potenza Producciones Fusileros la película AIE Release dates 12 November 2020 (2020-11-12) (Punto Play) 1...