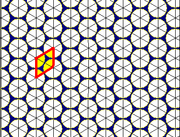
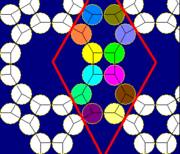
Упаковка кругов
|
Read other articles:

David CasaMEPMember of the European Parliamentfor MaltaIncumbentAssumed office 20 July 2004 Personal detailsBorn (1968-11-16) November 16, 1968 (age 54)VallettaNationalityMaltesePolitical partyPartit NazzjonalistaOther politicalaffiliationsEuropean's People PartyKnown forSocial rights, rule of law and anti-corruption activism, media freedomCommitteesCommittee on Employment and Social Rights, Committee on Economic and Monetary AffairsWebsitedavidcasa.eu David Casa (born 16 November 19...

موبيج شعار الاسم الرسمي (بالفرنسية: Maubeuge) الإحداثيات 50°16′37″N 3°58′21″E / 50.276944444444°N 3.9725°E / 50.276944444444; 3.9725[1] [2] تاريخ التأسيس 661 تقسيم إداري البلد فرنسا[3][4] التقسيم الأعلى نور خصائص جغرافية المساحة 18.85 كيلومتر مربع...

Maurice Carême, Sommer 1970, Margny, bei d’OrvalFoto: Jeannine Burny, La Fondation Maurice Carême Maurice Carême (* 12. Mai 1899 in Wavre; † 13. Januar 1978 in Anderlecht) war ein belgischer Schriftsteller. Carême stammte aus einfachen Verhältnissen; sein Vater war Maler, seine Mutter betrieb einen kleinen Laden. Er war ein sehr guter Schüler und erhielt daher ein Stipendium, das ihm den Besuch der École normale primaire von Tirlemont ermöglichte. 1918 erhielt er eine Stelle als L...

لمعانٍ أخرى، طالع تايلر ويلسون (توضيح). هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2018) تايلر ويلسون معلومات شخصية الميلاد 26 مايو 1989 (34 سنة) تشينو هيلس، سان بيرناردينو، كاليفورنيا الطول 5 قد...

Artikel ini mendokumentasikan suatu wabah penyakit terkini. Informasi mengenai hal itu dapat berubah dengan cepat jika informasi lebih lanjut tersedia; laporan berita dan sumber-sumber primer lainnya mungkin tidak bisa diandalkan. Pembaruan terakhir untuk artikel ini mungkin tidak mencerminkan informasi terkini mengenai wabah penyakit ini untuk semua bidang. Artikel ini memerlukan pemutakhiran informasi. Harap perbarui artikel dengan menambahkan informasi terbaru yang tersedia. Pembaruan tera...

لمعانٍ أخرى، طالع الجرن (توضيح). الجرن - قرية مصرية - تقسيم إداري البلد مصر المحافظة محافظة البحيرة المركز أبو حمص المسؤولون السكان التعداد السكاني 7041 نسمة (إحصاء 2006) معلومات أخرى التوقيت ت ع م+02:00 تعديل مصدري - تعديل قرية الجرن هي إحدى القرى التاب...

Science during the 16th-19th century Table of astronomy, from the 1728 Cyclopaedia The history of science during the Age of Enlightenment traces developments in science and technology during the Age of Reason, when Enlightenment ideas and ideals were being disseminated across Europe and North America. Generally, the period spans from the final days of the 16th and 17th-century Scientific Revolution until roughly the 19th century, after the French Revolution (1789) and the Napoleonic era (1799...

Amusement park in Ohio For other uses, see King's Island (disambiguation). Kings IslandPreviously known as Paramount's Kings Island (1993–2006)Kings Island's original fountains with Eiffel TowerLocationMason, Ohio, U.S.Coordinates39°20′41.23″N 84°16′06.99″W / 39.3447861°N 84.2686083°W / 39.3447861; -84.2686083StatusOperatingOpenedApril 29, 1972 (1972-04-29)OwnerCedar FairGeneral managerMichael KoontzSloganIt's Amazing In Here[1]Oper...

Trotskyite, Left-wing organization in Pakistan The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (November 2018) (Learn how and when to remove this template message) The Struggle طبقاتی جدوجہدFounderLal KhanFounded1980HeadquartersKarachi, PakistanIdeologyCommunismTrotskyism[1]Political positionLeftColors Red Black WhiteWebsitehttp://struggl...

В Википедии есть статьи о других людях с именем Людвиг. Людвиг X Баварскийнем. Ludwig X. von Bayern герцог Баварии Предшественник Вильгельм IV Преемник Вильгельм IV (герцог Баварии) Рождение 18 сентября 1495Грюнвальд, Мюнхен, Верхняя Бавария, Бавария Смерть 22 апреля 1545 (49 лет)Ландсху�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. How Democracies Die PengarangSteven Levitsky, Daniel ZiblattPerancang sampulChristopher BrandNegaraAmerika SerikatSubjekPolitikTeori politikPenerbitCrown (penerbit)Tanggal terbit16 Januari 2018 (2018-01-16)Jenis mediaPrint (sampul k...

Constituency of the Kerala legislative assembly in India KayamkulamConstituency for theCoconut tree orchard near KayamkulamConstituency detailsCountryIndiaDistrictAlappuzhaEstablished1957 - presentTotal electors2,03,308 (2016)ReservationNoneMember of Legislative AssemblyIncumbent U. Prathibha PartyCPI(M)Alliance LDFElected year2021 Kayamkulam State assembly constituency is one of the 140 state legislative assembly constituencies at the state Kerala in southern India. It is also one...

Piano Quartet in C minorPiano quartet by Richard StraussCover page of first editionKeyC minorCatalogueTrV 137Opus13Composed1884–1885DedicationGeorg II, Duke of Saxe-MeiningenPublished1886 (1886)Duration37–40 minutesMovementsfourScoringpianoviolinviolacelloPremiereDate8 December 1885 (1885-12-08)LocationWeimarPerformersRichard Strauss (piano)Karel Halíř (violin)Hagel (viola)Leopold Grützmacher (cello) Strauss in 1886 The Piano Quartet in C minor, Op. 13, TrV 137, was...

MyraΜύρα (Yunani Kuno)Teater Myra, dengan makam batu-batuan Lykia nekropolis di atas tebing sebagai latar belakangnya.Lokasi di TurkiLokasiDemre, Provinsi Antalya, TurkiWilayahLykiaKoordinat36°15′32.62″N 29°59′6.63″E / 36.2590611°N 29.9851750°E / 36.2590611; 29.9851750Koordinat: 36°15′32.62″N 29°59′6.63″E / 36.2590611°N 29.9851750°E / 36.2590611; 29.9851750JenisSettlement Myra (bahasa Yunani Kuno: Μύρα, Mýra)...

Fourth season of the AMC crime drama television series Season of television series Breaking BadSeason 4Season 4 DVD coverStarring Bryan Cranston Anna Gunn Aaron Paul Dean Norris Betsy Brandt RJ Mitte Bob Odenkirk Giancarlo Esposito Jonathan Banks Country of originUnited StatesNo. of episodes13ReleaseOriginal networkAMCOriginal releaseJuly 17 (2011-07-17) –October 9, 2011 (2011-10-09)Season chronology← PreviousSeason 3Next →Season 5List of episodes The fourth sea...

River StreetRiver Street station in 2010, focusing on the former staircase to the platform.General informationLocationRiver Street & Putnam Street, Paterson, New JerseyCoordinates40°55′44″N 74°09′45″W / 40.9288°N 74.1624°W / 40.9288; -74.1624Owned byErie Railroad (1883–1960)Erie-Lackawanna Railway (1960–1976)Conrail (1976–1977)Line(s)Erie Railroad Main Line (until 1963)Tracks2 main lineConstructionPlatform levels1Other informationStati...

Karkur redirects here. For the village in northern Syria, see Qarqur. Local council in IsraelPardes Hanna-Karkur פַּרְדֵּס חַנָּה-כַּרְכּוּרLocal councilHebrew transcription(s) • ISO 259Pardes Ḥanna - KarkurPardes Hanna-KarkurShow map of Haifa region of IsraelPardes Hanna-KarkurShow map of IsraelCoordinates: 32°28′16″N 34°58′03″E / 32.47111°N 34.96750°E / 32.47111; 34.96750Country IsraelDistrict H...

12th/13th-century Danish historian Saxo, drawn by the Norwegian illustrator Louis Moe. Saxo Grammaticus (c. 1150 – c. 1220), also known as Saxo cognomine Longus, was a Danish historian, theologian and author. He is thought to have been a clerk or secretary to Absalon, Archbishop of Lund, the main advisor to Valdemar I of Denmark. He is the author of the Gesta Danorum, the first full history of Denmark, from which the legend of Amleth would come to inspire the story of Hamle...

Indian actress (born 2001) This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. See Wikipedia's guide to writing better articles for suggestions. (March 2022) (Learn how and when to remove this template message) Avneet KaurKaur in 2022Born (2001-10-13) 13 October 2001 (age 22)Jalandhar, Punjab, IndiaOccupationsActressdancerYears active2010–presentKnown forDance India Dance Li'l MastersChandra NandiniAladdin – Naam Toh Suna Hoga Avneet Kaur (...

Soviet military personnel Andrei SnesarevAndrei Snesarev, inspecting the 7th fighter squadron on the eastern front, approximately March 1917, during the First World War. Ivan Orlov on the rightBorn13 December 1865Staraya Kalitva, Russian EmpireDied4 December 1937 (aged 71)Moscow, Soviet UnionAllegiance Russian Empire (1888–17) Soviet Russia (1918–22) Soviet Union(1922–1928)Service/branch Russian Imperial Army (1888–1917) Red Army (1918–28)RankLieutenant GeneralUnit2nd Combined Cossa...