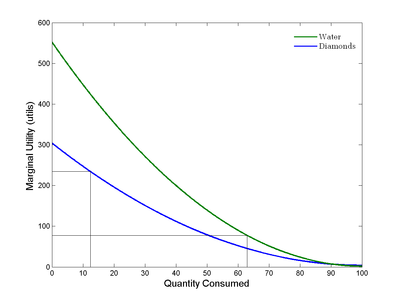
Предельная полезность
|
Read other articles:

Shire of Warren Local Government Area van Australië Ligging van Shire of Warren in Nieuw-Zuid-Wales Situering Staat Nieuw-Zuid-Wales Hoofdplaats Warren Coördinaten 31°42'ZB, 147°50'OL Algemene informatie Oppervlakte 10.760,3[1] km² Inwoners 2833 (juni 2009)[2] Overig Wards 4 Portaal Australië Shire of Warren is een Local Government Area (LGA) in Australië in de staat Nieuw-Zuid-Wales. Shire of Warren telt 2833 inwoners. De hoofdplaats is Warren. Plaatsen Sh...

Hàm Minh Xã Xã Hàm Minh Hành chínhQuốc gia Việt NamVùngDuyên hải Nam Trung BộTỉnhBình ThuậnHuyệnHàm Thuận NamĐịa lýTọa độ: 10°51′17″B 107°55′13″Đ / 10,85472°B 107,92028°Đ / 10.85472; 107.92028 Hàm Minh Vị trí xã Hàm Minh trên bản đồ Việt Nam Diện tích81,18 km²[1]Dân số (1999)Tổng cộng7531 người[1]Mật độ93 người/km²KhácMã hành chính23137[2]xts Hàm Minh là m

Vous lisez un « article de qualité » labellisé en 2012. Pour les articles homonymes, voir Ringo, Starr et Starkey. Ringo Starr Ringo Starr en 2019.Informations générales Surnom Ring', Richie Nom de naissance Richard Starkey Naissance 7 juillet 1940 (83 ans) Liverpool, Royaume-Uni Activité principale Musicien, chanteur, auteur-compositeur-interprète, acteur, producteur de cinéma Genre musical Pop rock, rock ’n’ roll, country Instruments Batterie, percussions, chant,...

Annual college football game between the two largest Kentucky universities See also: Kentucky–Louisville rivalry Kentucky–Louisville football rivalry Kentucky Wildcats Louisville Cardinals SportFootballFirst meetingOctober 26, 1912Kentucky, 41–0Latest meetingNovember 25, 2023Kentucky, 38–31Next meetingNovember 30, 2024 (Lexington)StadiumsKentucky - Kroger FieldLouisville - Cardinal StadiumTrophyThe Governor's CupStatisticsMeetings total35All-time seriesKentucky, 20–15[1]Larg...

Series of protests, mostly in Madrid This article needs to be updated. Please help update this article to reflect recent events or newly available information. (December 2023) 2023 Spanish protestsPart of 2023 Spanish government formationDemonstration in Plaza de Colón on 29 October 2023 (top); protest against the amnesty in Calle de Ferraz on 6 November (bottom)Date29 October 2023 – present(1 month and 5 days)LocationSpain, primarily MadridCaused by Negotiations to form a new go...

Motor racing championship held in 2023 2023 FIA Formula 3 Championship Drivers' Champion: Gabriel BortoletoTeams' Champion: Prema Racing Previous 2022 Next 2024 Parent series:Formula One World ChampionshipFormula 2 Championship Support series:Porsche Supercup The 2023 FIA Formula 3 Championship was a motor racing championship for Formula 3 cars sanctioned by the Fédération Internationale de l'Automobile (FIA). The championship was the fourteenth season of Formula 3 racing and the fifth seas...

Jane FromanInformasi latar belakangNama lahirEllen Jane FromanLahir(1907-11-10)10 November 1907University City, MissouriMeninggal22 April 1980(1980-04-22) (umur 72)Columbia, MissouriPekerjaanPenyanyi, pemeranSitus webwww.janefroman.com Ellen Jane Froman (10 November 1907 – 22 April 1980) adalah seorang penyanyi dan pemeran Amerika Serikat. Pada masa karirnya selama tiga puluh tahun , Froman pentas di panggung, radio dan televisi meskipun mengalami masalah kesehatan kronis...

For the album, see Friday on My Mind (album). For the television series, see Friday on My Mind (miniseries). 1966 single by The EasybeatsFriday on My MindCover of the 1966 Australian singleSingle by The Easybeatsfrom the album Good Friday B-sideMade My Bed, Gonna Lie in ItReleased 14 October 1966 (UK) 17 November 1966 (Australia) Recorded8 September 1966StudioIBC Studios, LondonGenre Garage rock[1] proto-punk[2] psychedelia[3] power pop[4] Length2:47LabelUnited...

French royal chapel in Paris, France Sainte-ChapelleSainte-Chapelle, upper level interiorReligionAffiliationCatholic ChurchProvinceArchdiocese of ParisRegionÎle-de-FranceRiteRoman RiteStatusSecularized since French RevolutionLocationLocation10, boulevard du Palais, 1st arrondissementMunicipalityParisCountryFranceGeographic coordinates48°51′19″N 2°20′42″E / 48.85528°N 2.34500°E / 48.85528; 2.34500ArchitectureTypeParish churchStyleFrench GothicGroundbreaking...

Jurisdictional speed limits in the U.S. Main article: Speed limits in the United States This article may be too long to read and navigate comfortably. Please consider splitting content into sub-articles, condensing it, or adding subheadings. Please discuss this issue on the article's talk page. (January 2021) Maximum speed limits in the U.S. states (or counties in the case of Minnesota and Texas) Maximum speed limits in the U.S. territories Speed limits in the United States vary depending on ...

Protein-coding gene in the species Homo sapiens ZNF365IdentifiersAliasesZNF365, Su48, UAN, ZNF365D, zinc finger protein 365External IDsOMIM: 607818 MGI: 2143676 HomoloGene: 8975 GeneCards: ZNF365 Gene location (Human)Chr.Chromosome 10 (human)[1]Band10q21.2Start62,374,192 bp[1]End62,480,288 bp[1]Gene location (Mouse)Chr.Chromosome 10 (mouse)[2]Band10|10 B5.1Start67,721,933 bp[2]End67,748,492 bp[2]RNA expression patternBgeeHumanMouse (ortholo...

American basketball player (1904–1966) Jack CobbPersonal informationBorn(1904-08-04)August 4, 1904Durham, North CarolinaDiedSeptember 9, 1966(1966-09-09) (aged 62)Greenville, North CarolinaNationalityAmericanListed height6 ft 2 in (1.88 m)Listed weight175 lb (79 kg)Career informationHigh schoolWoodberry Forest(Woodberry Forest, Virginia)CollegeNorth Carolina (1923–1926)PositionForwardCareer highlights and awards 3× Consensus All-American (1924–1926) 3× Al...

Unhabitable areas around Christchurch, New Zealand Map of residential red zone in and around Christchurch, New Zealand A residential red zone is any of several areas of land in and around Christchurch, New Zealand, that experienced severe damage in the 2010 and 2011 Christchurch earthquakes and were deemed infeasible to rebuild on. Through voluntary buyouts, the Crown acquired and demolished or removed over 8,000 properties.[1]: 5 The majority were located in a broad ...

Disparaging term used by opponents of gay rights activism Gay propaganda redirects here. For the 2013 Russian law, see Russian gay propaganda law. Gay agenda or homosexual agenda is a term used by sectors of the Christian religious right as a disparaging way to describe the advocacy of cultural acceptance and normalization of non-heterosexual sexual orientations and relationships. The term originated among social conservatives in the United States and has been adopted in nations with active a...

Indian startup business reality television series Shark Tank IndiaGenreReality televisionBased onShark TankPresented byRannvijay Singh(season 1) Rahul Dua(season 2 - present)Starring Ashneer Grover (season 1) Anupam Mittal (season 1–present) Ghazal Alagh (season 1) Namita Thapar (season 1–present) Peyush Bansal (season 1–present) Vineeta Singh (season 1–present) Aman Gupta (season 1–present) Amit Jain (season 2–present) Country of originIndiaOriginal languageHindiNo. of seasons2No...

1964 novel by Leigh Brackett The Secret of Sinharat Cover of first edition.AuthorLeigh BrackettCountryUnited StatesLanguageEnglishGenreScience fictionPublisherAce BooksPublication date1964Media typePrint (Paperback)Pages95Followed byPeople of the Talisman The Secret of Sinharat is a science fantasy novel by American writer Leigh Brackett, set on the planet Mars, whose protagonist is Eric John Stark. The novel is expanded from the novella Queen of the Martian Catacombs, publish...

1989 studio album by Loudon Wainwright IIITherapyStudio album by Loudon Wainwright IIIReleased1989RecordedSeptember–October 1988StudioElephant Studios, Wapping, LondonGenreFolkLength46:11LabelSilvertoneProducerChaim Tannenbaum,Loudon Wainwright IIILoudon Wainwright III chronology More Love Songs(1986) Therapy(1989) History(1992) Professional ratingsReview scoresSourceRatingAllMusic[1]Robert ChristgauB+[2] Therapy is a 1989 album by Loudon Wainwright III. It followed ...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (April 2020) Najah Al-Masa’eedنجاح المساعيدBorn (1977-10-16) 16 October 1977 (age 46)Al-Mafraq, JordanNationalityEmiratiEducationB.A. of Sociology (Mu'tah University)OrganizationHonorary member in the “Poets of the Homeland” groupKnown forAdvocate for human rights, peace and justice, author, Arms Trade Treaty...

Mitrailleuse Hotchkiss de 13,2 mm modèle 1929 Тип Крупнокалиберный пулемёт Страна Франция История службы Годы эксплуатации с 1930 Войны и конфликты Вторая мировая война История производства Производитель Hotchkiss et Cie Годы производства 1930 Характеристики Масса, кг 40 кг (на станке — 97 кг) Длина, мм...

Annual observance, October 4–10 World Space WeekWorld Space Week logoObserved byWorldwideTypeUnited NationsObservancesmore than 95 countriesBeginsOctober 4EndsOctober 10DateOctober 4Frequencyannual World Space Week (WSW) is an annual holiday observed from October 4 to 10 in over 95 nations throughout the world. World Space Week is officially defined as an international celebration of science and technology, and their contribution to the betterment of the human condition.[1] Wor...