![]() –Ď–į–Ľ–į–Ľ–į—Ä–ī—č –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź“ď—č “Į–Ļ—Ä–Ķ—ā—Ė–Ņ –ĺ—ā—č—Ä“ď–į–Ĺ ”ô–Ļ–Ķ–Ľ. –≠–≤–ļ–Ľ–ł–ī—ā—č“£ ¬ę–Ď–į—Ā—ā–į–ľ–į¬Ľ –į—ā—ā—č –ļ—Ė—ā–į–Ī—č–Ĺ–ī–į“ď—č (XIV “ď.) —Ā—É—Ä–Ķ—ā
–Ď–į–Ľ–į–Ľ–į—Ä–ī—č –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź“ď—č “Į–Ļ—Ä–Ķ—ā—Ė–Ņ –ĺ—ā—č—Ä“ď–į–Ĺ ”ô–Ļ–Ķ–Ľ. –≠–≤–ļ–Ľ–ł–ī—ā—č“£ ¬ę–Ď–į—Ā—ā–į–ľ–į¬Ľ –į—ā—ā—č –ļ—Ė—ā–į–Ī—č–Ĺ–ī–į“ď—č (XIV “ď.) —Ā—É—Ä–Ķ—ā
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź (–ļ”©–Ĺ–Ķ –≥—Ä–Ķ–ļ—ą–Ķ: ő≥őĶŌČőľőĶŌĄŌĀőĮőĪ; –ļ”©–Ĺ–Ķ –≥—Ä–Ķ–ļ—ą–Ķ: ő≥ŠŅÜ ‚ÄĒ –∂–Ķ—Ä –ł –ļ”©–Ĺ–Ķ –≥—Ä–Ķ–ļ—ą–Ķ: őľőĶŌĄŌĀő≠ŌČ ‚ÄĒ ¬ę”©–Ľ—ą–Ķ—ɬĽ) ‚ÄĒ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į–Ĺ—č“£ –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ –Ņ—Ė—ą—Ė–Ĺ–ī–Ķ—Ä (—Ą–ĺ—Ä–ľ–į–Ľ–į—Ä) –ľ–Ķ–Ĺ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä–ī—č, —Ā–ĺ–Ĺ–ī–į–Ļ-–į“õ, –ĺ–Ľ–į—Ä“ď–į “Ī“õ—Ā–į—Ā –Ī–į—Ā“õ–į –ī–į –Ņ—Ė—ą—Ė–Ĺ–ī–Ķ—Ä –ľ–Ķ–Ĺ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä–ī—č –∑–Ķ—Ä—ā—ā–Ķ–Ļ—ā—Ė–Ĺ —Ā–į–Ľ–į—Ā—č. “í—č–Ľ—č–ľ —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ –ē–∂–Ķ–Ľ–≥—Ė –ď—Ä–Ķ–ļ–ł—Ź–ī–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į–Ĺ—č“£ –Ī—Ė—Ä –Ī”©–Ľ—Ė–≥—Ė –Ī–ĺ–Ľ—č–Ņ “õ–į–Ľ—č–Ņ—ā–į—Ā“õ–į–Ĺ, –ĺ–Ĺ—č“£ –į–Ľ“ď–į—ą“õ—č –į–ļ—Ā–ł–ĺ–ľ–į–Ľ–į—Ä—č –ē–≤–ļ–Ľ–ł–ī—ā—Ė“£ ¬ę–Ě–Ķ–≥—Ė–∑–ī–Ķ—Ä—Ė¬Ľ –ļ—Ė—ā–į–Ī—č–Ĺ–ī–į —Ā–ł–Ņ–į—ā—ā–į–Ľ“ď–į–Ĺ.
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —ā–į–Ī–ł“ď–į—ā—ā—č –∑–Ķ—Ä—ā—ā–Ķ—É–ī–Ķ, —ā–Ķ—Ö–Ĺ–ł–ļ–į–Ĺ—č –ī–į–ľ—č—ā—É–ī–į “õ—É–į—ā—ā—č “õ“Ī—Ä–į–Ľ –Ī–ĺ–Ľ—č–Ņ —ā–į–Ī—č–Ľ–į–ī—č. –ě–Ľ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į–Ľ—č“õ –į–Ĺ–į–Ľ–ł–∑–≥–Ķ, –ľ–Ķ—Ö–į–Ĺ–ł–ļ–į“ď–į, —Ą–ł–∑–ł–ļ–į“ď–į, –į—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ–ł—Ź“ď–į, –≥–Ķ–ĺ–ī–Ķ–∑–ł—Ź“ď–į, –ļ–į—Ä—ā–ĺ–≥—Ä–į—Ą–ł—Ź“ď–į, –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–ĺ–≥—Ä–į—Ą–ł—Ź“ď–į, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į “ď—č–Ľ—č–ľ–ī–į—Ä“ď–į –Ķ–Ľ–Ķ—É–Ľ—Ė —č“õ–Ņ–į–Ľ –Ķ—ā–Ķ–ī—Ė.
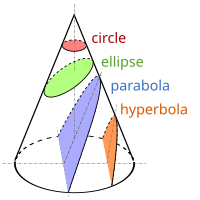 –ö–ĺ–Ĺ—É—Ā—ā—č“£ “õ–ł–ľ–į–Ľ–į—Ä—č: —ą–į—Ä, —ć–Ľ–Ľ–ł–Ņ—Ā, –Ņ–į—Ä–į–Ī–ĺ–Ľ–į, –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–į
–ö–ĺ–Ĺ—É—Ā—ā—č“£ “õ–ł–ľ–į–Ľ–į—Ä—č: —ą–į—Ä, —ć–Ľ–Ľ–ł–Ņ—Ā, –Ņ–į—Ä–į–Ī–ĺ–Ľ–į, –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–į
–§–ł–≥—É—Ä–į–Ľ–į—Ä - –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ –Ņ—Ė—ą—Ė–Ĺ–ī–Ķ—Ä –Ī–ĺ–Ľ—č–Ņ –Ķ—Ā–Ķ–Ņ—ā–Ķ–Ľ–Ķ–ī—Ė. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —ā“Ī—Ä“ď—č—Ā—č–Ĺ–į–Ĺ —Ā—č–∑—č“õ ‚ÄĒ ‚Äú—Ā—č–ľ‚ÄĚ –Ķ–ľ–Ķ—Ā, —ą–į—Ä ‚ÄĒ ‚Äú–ī–ĺ–ľ–į–Ľ–į“õ –ī–Ķ–Ĺ–Ķ‚ÄĚ –Ķ–ľ–Ķ—Ā, –ĺ–Ľ–į—Ä–ī—č“£ –Ī–į—Ä–Ľ—č“ď—č –ī–į ‚ÄĒ –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ –Ņ—Ė—ą—Ė–Ĺ–ī–Ķ—Ä. –ź–Ľ –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä ‚ÄĒ —Ą–ł–≥—É—Ä–į–Ľ–į—Ä–ī—č“£ –ľ”©–Ľ—ą–Ķ—Ä—Ė –ľ–Ķ–Ĺ –ĺ—Ä–Ĺ–į–Ľ–į—Ā—É—č–Ĺ –į–Ĺ—č“õ—ā–į–Ļ–ī—č. –ú—č—Ā–į–Ľ—č, —Ü–Ķ–Ĺ—ā—Ä–Ľ–Ķ—Ä—Ė –ĺ—Ä—ā–į“õ, —Ä–į–ī–ł—É—Ā—ā–į—Ä—č 3 —Ā–ľ –∂”ô–Ĺ–Ķ 5 —Ā–ľ —ą–Ķ“£–Ī–Ķ—Ä–Ľ–Ķ—Ä “õ–ł—č–Ľ—č—Ā–Ņ–į–Ļ–ī—č, ‚Äú–Ī—Ė—Ä—Ė–Ĺ—ą—Ė—Ā—Ė –Ķ–ļ—Ė–Ĺ—ą—Ė—Ā—Ė–Ĺ—Ė“£ —Ė—ą—Ė–Ĺ–ī–Ķ –∂–į—ā–į–ī—č‚ÄĚ –ī–Ķ–≥–Ķ–Ĺ–ī–Ķ ‚ÄĒ —ą–Ķ“£–Ī–Ķ—Ä–Ľ–Ķ—Ä–ī—Ė“£ –ľ”©–Ľ—ą–Ķ—Ä—Ė –ľ–Ķ–Ĺ –ĺ—Ä–Ĺ–į–Ľ–į—Ā—É—č –∂”©–Ĺ—Ė–Ĺ–ī–Ķ –į–Ļ—ā—č–Ľ—č–Ņ —ā“Ī—Ä. –ú“Ī–Ĺ–ī–į –Ī—Ė—Ä—Ė–Ĺ—ą—Ė —ą–Ķ“£–Ī–Ķ—Ä ‚ÄĒ –ļ—Ė—ą—Ė—Ā—Ė, –Ķ–ļ—Ė–Ĺ—ą—Ė—Ā—Ė ‚ÄĒ “Į–Ľ–ļ–Ķ–Ĺ—Ė, –Ī—Ė—Ä—Ė–Ĺ—ą—Ė—Ā—Ė –Ķ–ļ—Ė–Ĺ—ą—Ė—Ā—Ė–Ĺ—Ė“£ —Ė—ą—Ė–Ĺ–ī–Ķ –ĺ—Ä–Ĺ–į–Ľ–į—Ā“õ–į–Ĺ. –ě—Ā—č“ď–į–Ĺ –ĺ—Ä–į–Ļ –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä ‚Äú“Į–Ľ–ļ–Ķ–Ĺ‚ÄĚ, ‚Äú–ļ—Ė—ą—Ė‚ÄĚ, ‚Äú—Ė—ą—Ė–Ĺ–ī–Ķ‚ÄĚ, ‚Äú—Ā—č—Ä—ā—č–Ĺ–ī–į‚ÄĚ —Ā”©–∑–ī–Ķ—Ä—Ė –į—Ä“õ—č–Ľ—č –į–Ĺ—č“õ—ā–į–Ľ“ď–į–Ĺ. ‚Äú–Ę–Ķ“£‚ÄĚ, ‚Äú–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć‚ÄĚ, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į —Ā”©–∑–ī–Ķ—Ä –ī–Ķ –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä–ī—č —Ā–ł–Ņ–į—ā—ā–į–Ļ–ī—č.[1]
–Ē–Ķ–Ĺ–Ķ–Ĺ—Ė“£ —ą–Ķ–ļ–į—Ä–į—Ā—č ‚ÄĒ –Ī–Ķ—ā. –ě–Ľ –ī–Ķ–Ĺ–Ķ–Ĺ—Ė “õ–į–Ņ—ā–į–Ņ, “õ–ĺ—Ä—ą–į–Ņ, —ą–Ķ–ļ—ā–Ķ–Ņ, –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ–Ĺ –Ī”©–Ľ—Ė–Ņ —ā“Ī—Ä–į–ī—č. –Ď–Ķ—ā —ą–Ķ–ļ—ā–Ķ—É—Ā—Ė–∑ –∂“Ī“õ–į –Ī–ĺ–Ľ—č–Ņ –Ķ—Ā–Ķ–Ņ—ā–Ķ–Ľ–Ķ–ī—Ė. –Ė—Ė“£—Ė—ą–ļ–Ķ –∂—Ė–Ņ, –Ī—Ė—Ä —ā–į–Ľ “õ—č–Ľ, —Ā”ô—É–Ľ–Ķ, —Ā—č–ľ, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į –Ĺ–Ķ–≥—Ė–∑—Ė–Ĺ–ī–Ķ —ą–Ķ–ļ—ā–Ķ—É—Ā—Ė–∑ –∂—Ė“£—Ė—ą–ļ–Ķ —Ā—č–∑—č“õ “Ī“ď—č–ľ—č —ą—č“õ“õ–į–Ĺ. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ—č“õ –ī–Ķ–Ĺ–Ķ–Ľ–Ķ—Ä–ī—Ė –ĺ–Ļ—ą–į —ā–ĺ–Ņ—ą—č–Ľ–į–Ņ, —ą–Ķ–ļ—ā–Ķ—É—Ā—Ė–∑ –ļ—Ė—ą—Ė—Ä–Ķ–Ļ—ā–Ķ –Ī–Ķ—Ä—É–≥–Ķ –Ī–ĺ–Ľ–į–ī—č. –ě—Ā—č–ī–į–Ĺ –Ĺ“Į–ļ—ā–Ķ “Ī“ď—č–ľ—č —ą—č“ď–į–ī—č. –Ě“Į–ļ—ā–Ķ –ī–Ķ–Ĺ–Ķ–Ĺ—Ė“£ ”ô–Ī–ī–Ķ–Ĺ –ļ—Ė—ą—Ė—Ä–Ķ–Ļ—Ė–Ņ, —ā–ĺ“õ—ā–į“ď–į–Ĺ —ą–Ķ–ļ—ā—Ė–ļ –∂–į“ď–ī–į–Ļ—č –ī–Ķ–Ņ –Ķ—Ā–Ķ–Ņ—ā–Ķ–Ľ–Ķ–ī—Ė. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —ā“Ī—Ä“ď—č—Ā—č–Ĺ–į–Ĺ –į–Ľ“ď–į–Ĺ–ī–į –Ĺ“Į–ļ—ā–Ķ–Ĺ—Ė –ĺ–ī–į–Ĺ ”ô—Ä—Ė –ļ—Ė—ą—Ė—Ä–Ķ–Ļ—ā—É–≥–Ķ –Ī–ĺ–Ľ–ľ–į–Ļ–ī—č. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ—č“õ –ī–Ķ–Ĺ–Ķ–Ľ–Ķ—Ä–ī—Ė“£, –Ī–Ķ—ā—ā–Ķ—Ä–ī—Ė“£, —Ā—č–∑—č“õ—ā–į—Ä–ī—č“£ –∂”ô–Ĺ–Ķ –Ĺ“Į–ļ—ā–Ķ–Ľ–Ķ—Ä–ī—Ė“£ –ļ–Ķ–∑ –ļ–Ķ–Ľ–≥–Ķ–Ĺ –∂–ł—č–Ĺ—č —Ą–ł–≥—É—Ä–į –ī–Ķ–Ņ –į—ā–į–Ľ–į–ī—č. –ź–Ļ—ā—č–Ľ—č–Ņ –ĺ—ā—č—Ä“ď–į–Ĺ –Ĺ–Ķ–≥—Ė–∑–≥—Ė “Ī“ď—č–ľ–ī–į—Ä ‚ÄĒ –Ĺ“Į–ļ—ā–Ķ, —Ā—č–∑—č“õ, –Ī–Ķ—ā, –ī–Ķ–Ĺ–Ķ –ī“Į–Ĺ–ł–Ķ–ī–Ķ–≥—Ė –∑–į—ā—ā–į—Ä–ī–į–Ĺ (—Ź“ď–Ĺ–ł, –ľ–į—ā–Ķ—Ä–ł—Ź–ī–į–Ĺ) –į–Ľ—č–Ĺ“ď–į–Ĺ. –Ď—Ė—Ä–į“õ –ľ–į—ā–Ķ—Ä–ł—Ź–Ĺ—č“£ —Ą–ł–∑–ł–ļ–į–Ľ—č“õ “õ–į—Ā–ł–Ķ—ā—ā–Ķ—Ä—Ė–Ĺ–Ķ–Ĺ –į–Ī—Ā—ā—Ä–į–ļ—Ü–ł—Ź–Ľ–į–Ĺ“ď–į–Ĺ. –ú—č—Ā–į–Ľ—č, –Ņ—Ä–ł–∑–ľ–į –∂”©–Ĺ—Ė–Ĺ–ī–Ķ–≥—Ė —ā–Ķ–ĺ—Ä–Ķ–ľ–į–Ľ–į—Ä–ī—č –į“ď–į—ą—ā–į–Ĺ, —ā–į—Ā—ā–į–Ĺ, –ľ–Ķ—ā–į–Ľ–ī–į–Ĺ –∂–į—Ā–į–Ľ“ď–į–Ĺ –Ņ—Ä–ł–∑–ľ–į–Ľ–į—Ä–ī—č“£ –Ī”ô—Ä—Ė–Ĺ–Ķ –ī–Ķ –∂”ô–Ĺ–Ķ ”ô—Ä–ī–į–Ļ—č–ľ “õ–ĺ–Ľ–ī–į–Ĺ–į –Ī–Ķ—Ä—É–≥–Ķ –Ī–ĺ–Ľ–į–ī—č. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –į–Ľ“ď–į—ą“õ—č –ļ–Ķ–∑–ī–Ķ —Ą–ł–≥—É—Ä–į–Ľ–į—Ä–ī—č“£ –ľ”©–Ľ—ą–Ķ—Ä–Ľ–Ķ—Ä—Ė–Ĺ, ”©–∑–į—Ä–į –ĺ—Ä–Ĺ–į–Ľ–į—Ā—É —ā”ô—Ä—ā—Ė–Ī—Ė–Ĺ, –Ī—Ė—Ä —ā“Į—Ä–ī–Ķ–Ĺ –Ķ–ļ—Ė–Ĺ—ą—Ė —ā“Į—Ä–≥–Ķ –ļ”©—ą—É –∂–ĺ–Ľ–ī–į—Ä—č–Ĺ –∑–Ķ—Ä—ā—ā–Ķ–Ļ—ā—Ė–Ĺ “ď—č–Ľ—č–ľ –Ī–ĺ–Ľ–ī—č. –ě–Ĺ–ī–į —Ą–ł–≥—É—Ä–į–Ľ–į—Ä–ī—č“£ —ā“Į—Ä–Ľ–Ķ–Ĺ–ī—Ė—Ä—Ė–Ľ—É—Ė –Ī–Ķ—Ä—Ė–Ľ–≥–Ķ–Ĺ —Ą–ł–≥—É—Ä–į –ľ–Ķ–Ĺ –ļ–Ķ–Ļ—Ė–Ĺ –Ņ–į–Ļ–ī–į –Ī–ĺ–Ľ“ď–į–Ĺ —Ą–ł–≥—É—Ä–į–Ĺ—č“£ –į—Ä–į—Ā—č–Ĺ–ī–į“ď—č –Ī–Ķ–Ľ–≥—Ė–Ľ—Ė –Ī—Ė—Ä “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ —ā“Į—Ā—Ė–Ĺ–ī—Ė—Ä—Ė–Ľ–ī—Ė. –ú“Ī–Ĺ–ī–į–Ļ —ā“Į—Ā—Ė–Ĺ—Ė–ļ –ĺ—Ā—č –ļ“Į–Ĺ–≥—Ė –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–ī–į –ī–į –Ī–į—Ä. –ź–Ľ–į–Ļ–ī–į “õ–į–∑—Ė—Ä–≥—Ė –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ī–į–Ļ—č—Ä“ď—č —ā“Į—Ā—Ė–Ĺ—Ė–ļ—ā–Ķ—Ä —ą–Ķ–Ī—Ė–Ĺ–Ķ–Ĺ “Ī–∑–į–Ņ —ą—č“ď—č–Ņ –ļ–Ķ—ā—ā—Ė. –°–ĺ“£“ď—č “ď–į—Ā—č—Ä–Ľ–į—Ä–ī–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ “Į–Ļ—Ä–Ķ–Ĺ—ą—Ė–ļ—ā—Ė “Ī“ď—č–ľ–ī–į—Ä—č –ľ–Ķ–Ĺ “õ–į“ď–ł–ī–į–Ľ–į—Ä—č–Ĺ —ā–į–Ľ–ī–į—É, –∂–į–Ľ–Ņ—č–Ľ–į—É, –∂–į—Ä—ā—č–Ľ–į–Ļ ”©–∑–≥–Ķ—Ä—ā—É –∂”ô–Ĺ–Ķ –ĺ–ī–į–Ĺ ”ô—Ä—Ė –į–Ī—Ā—ā—Ä–į–ļ—Ü–ł—Ź–Ľ–į—É –Ĺ”ô—ā–ł–∂–Ķ—Ā—Ė–Ĺ–ī–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į–Ĺ—č“£ –Ī—Ė—Ä—ā–į–Ľ–į–Ļ –∂–Ķ–ľ—Ė—Ā—ā—Ė —ā–Ķ–ĺ—Ä–ł—Ź–Ľ–į—Ä—č —ą—č“õ—ā—č. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –∂–į“£–į —Ā–į–Ľ–į–Ľ–į—Ä—č–Ĺ—č“£ –ļ”©–Ņ—ą—Ė–Ľ—Ė–≥—Ė –Ķ—Ä—ā–Ķ–ī–Ķ “õ–į–Ľ—č–Ņ—ā–į—Ā“õ–į–Ĺ –ī”ô—Ā—ā“Į—Ä–Ľ—Ė —Ā–į–Ľ–į–Ľ–į—Ä—č–Ĺ–į –ľ“Į–Ľ–ī–Ķ–ľ “Ī“õ—Ā–į–ľ–į–Ļ–ī—č. –ú—č—Ā–į–Ľ—č, –ď–Ķ–ĺ—Ä–≥ –§—Ä–ł–ī—Ä–ł—Ö –Ď–Ķ—Ä–Ĺ—Ö–į—Ä–ī –†–ł–ľ–į–Ĺ –ļ–Ķ“£—Ė—Ā—ā—Ė–≥—Ė–Ĺ–ī–Ķ–≥—Ė ‚Äú–į—Ä–į “õ–į—ą—č“õ—ā—č“õ‚ÄĚ, –ď–ł–Ľ—Ć–Ī–Ķ—Ä—ā –ļ–Ķ“£—Ė—Ā—ā—Ė–≥—Ė–Ĺ–ī–Ķ–≥—Ė ‚Äú–Ņ—Ä–ł–∑–ľ–į‚ÄĚ “Ī“ď—č–ľ–ī–į—Ä—č–Ĺ, –∂–į–Ľ–Ņ—č —ā“Į—Ä–ī–Ķ –į–Ľ“ď–į–Ĺ–ī–į, –Ķ—ą“õ–į–Ĺ–ī–į–Ļ —Ā—É—Ä–Ķ—ā, –ľ–ĺ–ī–Ķ–Ľ—Ć –Ī–ĺ–Ļ—č–Ĺ—ą–į —Ā–ł–Ņ–į—ā—ā–į—É“ď–į –Ī–ĺ–Ľ–ľ–į–Ļ–ī—č. –ě–Ľ–į—Ä–ī—č –ī“Į–Ĺ–ł–Ķ–ī–Ķ –ļ–Ķ–∑–ī–Ķ—Ā–Ķ—ā—Ė–Ĺ –Ĺ–į“õ—ā—č –Ĺ”ô—Ä—Ā–Ķ–Ľ–Ķ—Ä–ī—Ė“£ –Ņ—Ė—ą—Ė–Ĺ–ī–Ķ—Ä—Ė –ľ–Ķ–Ĺ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä—č –į—Ä“õ—č–Ľ—č —ā“Į—Ā—Ė–Ĺ–ī—Ė—Ä—É ”©—ā–Ķ “õ–ł—č–Ĺ. –°”©–Ļ—ā—Ā–Ķ –ī–Ķ, –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –Ī–į–Ļ—č—Ä“ď—č —Ā–į–Ľ–į–Ľ–į—Ä—č –∂–į“£–į —Ā–į–Ľ–į–Ľ–į—Ä—č–Ĺ—č“£ “õ–į—Ä–į–Ņ–į–Ļ—č–ľ –ī–Ķ—Ä–Ī–Ķ—Ā –ļ”©—Ä—Ė–Ĺ—Ė—Ā—ā–Ķ—Ä—Ė –Ī–ĺ–Ľ—č–Ņ —ā–į–Ī—č–Ľ–į–ī—č. –°”©–∑ –Ī–ĺ–Ľ—č–Ņ –ĺ—ā—č—Ä“ď–į–Ĺ –∂–į“£–į —ā–Ķ–ĺ—Ä–ł—Ź–Ľ–į—Ä–ī—č“£ “õ–į–Ļ—ą—č–Ľ—č“õ—Ā—č–∑–ī—č“ď—č –ľ“Ī“õ–ł—Ź—ā –ī”ô–Ľ–Ķ–Ľ–ī–Ķ–Ĺ–≥–Ķ–Ĺ –∂”ô–Ĺ–Ķ –ĺ–Ľ–į—Ä –ļ“Į–ľ”ô–Ĺ—Ā—Ė–∑. –°–ĺ“£“ď—č —Ā–į–Ľ–į–Ľ–į—Ä –ī–į, —ā–į—Ä–ł—Ö–ł –∂–į“ď—č–Ĺ–į–Ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —ą–į“£—č—Ä–į“ď—č–Ĺ—č“£ –į—Ā—ā—č–Ĺ–ī–į —ā—É“ď–į–Ĺ–ī—č“õ—ā–į–Ĺ –∂”ô–Ĺ–Ķ –ĺ–Ľ–į—Ä–ī—č“£ –∑–į“£–ī–į—Ä—č –Ī“Ī—Ä—č–Ĺ“ď—č –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –∑–į“£–ī–į—Ä—č–Ĺ–į —Ā—č—Ä—ā—ā–į–Ļ “Ī“õ—Ā–į—Ā –Ī–ĺ–Ľ“ď–į–Ĺ–ī—č“õ—ā–į–Ĺ, –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź“ď–į –∂–į—ā“õ—č–∑—č–Ľ–į–ī—č. –°”©–Ļ—ā—Ė–Ņ, –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ ”©—Ä—Ė—Ā—Ė –ľ“Į–Ľ–ī–Ķ–ľ –ļ–Ķ“£–Ķ–Ļ—Ė–Ņ –ļ–Ķ—ā—ā—Ė. –ě–Ĺ—č“£ –∂–ĺ“ď–į—Ä—č–ī–į –ļ–Ķ–Ľ—ā—Ė—Ä—Ė–Ľ–≥–Ķ–Ĺ –į–Ĺ—č“õ—ā–į–ľ–į—Ā—č–Ĺ–į ‚Äú—Ā–ĺ–Ĺ–ī–į–Ļ-–į“õ, –ĺ–Ľ–į—Ä“ď–į “Ī“õ—Ā–į—Ā –Ī–į—Ā“õ–į –ī–į –Ņ—Ė—ą—Ė–Ĺ–ī–Ķ—Ä –ľ–Ķ–Ĺ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä–ī—č –∑–Ķ—Ä—ā—ā–Ķ–Ļ—ā—Ė–Ĺ‚ÄĚ –ī–Ķ–≥–Ķ–Ĺ —Ā”©–∑–ī–Ķ—Ä —Ā–ĺ–Ĺ–ī—č“õ—ā–į–Ĺ “õ–ĺ—Ā—č–Ľ“ď–į–Ĺ. –ě—Ā—č–Ľ–į–Ļ –ļ–Ķ“£ –ľ–į“ď—č–Ĺ–į–ī–į —ā“Į—Ā—Ė–Ĺ–≥–Ķ–Ĺ –∂–į“ď–ī–į–Ļ–ī–į “ď–į–Ĺ–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į–Ĺ—č“£ –ļ”©–Ņ—ā–Ķ–≥–Ķ–Ĺ —Ā–į–Ľ–į—Ā—č–ľ–Ķ–Ĺ –į—Ā—ā–į—Ā—č–Ņ –∂–į—ā–į–ī—č.
–Ę–į—Ä–ł—Ö—č
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź ‚ÄĒ –Ķ—Ä—ā–Ķ –∑–į–ľ–į–Ĺ–ī–į—Ä–ī–į —ą—č“õ“õ–į–Ĺ “ď—č–Ľ—č–ľ–ī–į—Ä–ī—č“£ –Ī—Ė—Ä—Ė, –ĺ–Ĺ—č“£ —ā–į—Ä–ł—Ö—č –ī–į ”ô—Ä—Ė—Ä–Ķ–ļ—ā–Ķ–Ĺ –Ī–į—Ā—ā–į–Ľ–į–ī—č. –°–į–Ņ–į–Ľ—č“õ ”©–∑–≥–Ķ—Ä—Ė—Ā—ā–Ķ—Ä–≥–Ķ “Ī—ą—č—Ä–į–Ņ, –∂–į“£–į —Ā–į—ā—č–Ľ–į—Ä“ď–į –ļ”©—ā–Ķ—Ä—Ė–Ľ—É –ī”ô—Ä–Ķ–∂–Ķ—Ā—Ė–Ĺ–Ķ “õ–į—Ä–į–Ļ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –ī–į–ľ—É –∂–ĺ–Ľ—č–Ĺ 4 –ī”ô—É—Ė—Ä–≥–Ķ –Ī”©–Ľ—É–≥–Ķ –Ī–ĺ–Ľ–į–ī—č.

–Ď—Ė—Ä—Ė–Ĺ—ą—Ė –ī”ô—É—Ė—Ä ”©—ā–Ķ –Ķ—Ä—ā–Ķ –∑–į–ľ–į–Ĺ –ľ–Ķ–Ĺ –Ī—Ė–∑–ī—Ė“£ –∑–į–ľ–į–Ĺ—č–ľ—č–∑–ī–į–Ĺ –Ī“Ī—Ä—č–Ĺ 5 “ď–į—Ā—č—Ä –į—Ä–į–Ľ—č“ď—č–Ĺ “õ–į–ľ—ā–ł–ī—č. –Ď“Ī–Ľ –ī”ô—É—Ė—Ä–ī—Ė“£ –Ī–į—Ā—ā–į–Ľ“ď–į–Ĺ —É–į“õ—č—ā—č–Ĺ –ļ–Ķ—Ā—Ė–Ņ –į–Ļ—ā—É“ď–į –Ī–ĺ–Ľ–ľ–į–Ļ–ī—č. “ö–į—Ä–į–Ņ–į–Ļ—č–ľ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ—č“õ “Ī“ď—č–ľ–ī–į—Ä ”ô—Ä –ļ–Ķ–∑–ī–Ķ –∂”ô–Ĺ–Ķ ”ô—Ä –∂–Ķ—Ä–ī–Ķ —ą—č“õ“õ–į–Ĺ. –ź–Ľ“ď–į—ą“õ—č –ľ”ô–Ľ—Ė–ľ–Ķ—ā—ā–Ķ—Ä –ē–∂–Ķ–Ľ–≥—Ė –®—č“ď—č—Ā –Ķ–Ľ–ī–Ķ—Ä—Ė–Ĺ–ī–Ķ ‚ÄĒ –ú—č—Ā—č—Ä –ľ–Ķ–Ĺ –í–į–≤–ł–Ľ–ĺ–Ĺ–ī–į, –ď—Ä–Ķ–ļ–ł—Ź–ī–į, –ļ–Ķ–Ļ—Ė–Ĺ—Ė—Ä–Ķ–ļ “ģ–Ĺ–ī—Ė—Ā—ā–į–Ĺ–ī–į –Ņ–į–Ļ–ī–į –Ī–ĺ–Ľ“ď–į–Ĺ. –ē—Ä—ā–Ķ–ī–Ķ–≥—Ė –ľ—č—Ā—č—Ä–Ľ—č“õ—ā–į—Ä –Ě—Ė–Ľ–ī—Ė“£ –∂–į“ď–į—Ā—č–Ĺ–ī–į“ď—č “õ“Ī–Ĺ–į—Ä–Ľ—č —ā–ĺ–Ņ—č—Ä–į“õ“õ–į –Ī–ł–ī–į–Ļ –Ķ–≥—Ė–Ņ –ļ“Į–Ĺ–Ķ–Ľ—ā–ļ–Ķ–Ĺ. –Ě—Ė–Ľ –∂—č–Ľ —Ā–į–Ļ—č–Ĺ —ā–į—Ā—č–Ņ, –∂–į“ď–į–ī–į“ď—č –∂–Ķ—Ä —ā—Ė–Ľ—Ė–ľ–ī–Ķ—Ä—Ė–Ĺ—Ė“£ –Ī–Ķ–Ľ–≥—Ė–Ľ–Ķ–Ĺ–≥–Ķ–Ĺ —ą–Ķ–ļ–į—Ä–į–Ľ–į—Ä—č–Ĺ –Ī“Ī–∑—č–Ņ –ļ–Ķ—ā—Ė–Ņ –ĺ—ā—č—Ä“ď–į–Ĺ. –ź–Ľ —ą–į—Ä—É–į–Ľ–į—Ä —Ā—É “õ–į–Ļ—ā“õ–į–Ĺ —Ā–į–Ļ—č–Ĺ ”©–∑ –∂–Ķ—Ä–Ľ–Ķ—Ä—Ė–Ĺ ”©–Ľ—ą–Ķ–Ņ –Ī–į—Ä—č–Ņ, –į–Ļ—č—Ä—č–Ņ –į–Ľ–į—ā—č–Ĺ –Ī–ĺ–Ľ“ď–į–Ĺ. –£—á–į—Ā–ļ–Ķ–Ľ–Ķ—Ä–ī—Ė“£ “Ī–∑—č–Ĺ–ī—č“ď—č–Ĺ, –Ķ–Ĺ—Ė–Ĺ, –∂–ł–Ķ–ļ —Ā—č–∑—č“ď—č–Ĺ “Į–Ĺ–Ķ–ľ—Ė ”©–Ľ—ą–Ķ—É –Ĺ”ô—ā–ł–∂–Ķ—Ā—Ė–Ĺ–ī–Ķ “õ–į—Ä–į–Ņ–į–Ļ—č–ľ –Ķ—Ä–Ķ–∂–Ķ–Ľ–Ķ—Ä –Ņ–į–Ļ–ī–į –Ī–ĺ–Ľ“ď–į–Ĺ. –Ě—Ė–Ľ–ī—Ė“£ —ā–į—Ā–ł—ā—č–Ĺ –∂”ô–Ĺ–Ķ “õ–į–Ļ—ā–į—ā—č–Ĺ —É–į“õ—č—ā—ā–į—Ä—č–Ĺ –Ī–į“õ—č–Ľ–į—É –Ĺ”ô—ā–ł–∂–Ķ—Ā—Ė–Ĺ–ī–Ķ –ú—č—Ā—č—Ä –ļ“Į–Ĺ—ā—Ė–∑–Ī–Ķ—Ā—Ė —ą—č“õ“õ–į–Ĺ. –£–į“õ—č—ā –Ķ—Ā–Ķ–Ī—Ė –∂“Ī–Ľ–ī—č–∑–ī–į—Ä–ī—č“£ ”©–∑–į—Ä–į –∂”ô–Ĺ–Ķ –ļ”©–ļ–∂–ł–Ķ–ļ–Ņ–Ķ–Ĺ –∂–į—Ā–į–Ļ—ā—č–Ĺ –Ī“Ī—Ä—č—ą—ā–į—Ä—č–Ĺ (–Ī“Ī–Ľ –Ī“Ī—Ä—č—ą—ā–į—Ä–ī—č“£ —ā”©–Ī–Ķ–Ľ–Ķ—Ä—Ė –Ī–į“õ—č–Ľ–į—É—ą—č —ā“Ī—Ä“ď–į–Ĺ –∂–Ķ—Ä–ī–Ķ –Ī–ĺ–Ľ–į–ī—č) ”©–Ľ—ą–Ķ—É–ī—Ė “õ–į–∂–Ķ—ā –Ķ—ā–Ķ–ī—Ė. –ú—č—Ā—č—Ä –Ņ–į—ā—ą–į–Ľ–į—Ä—č ‚ÄĒ –Ņ–Ķ—Ä“ď–į—É—č–Ĺ–ī–į—Ä (—Ą–į—Ä–į–ĺ–Ĺ–ī–į—Ä) ”©–∑–ī–Ķ—Ä—Ė–Ĺ–Ķ –Ķ—Ā–ļ–Ķ—Ä—ā–ļ—Ė—ą –∂”ô–Ĺ–Ķ –∑–ł—Ä–į—ā —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ, —ā—Ė—Ä—Ė –ļ“Į–Ĺ–ī–Ķ—Ä—Ė–Ĺ–ī–Ķ, –∑”ô—É–Ľ—Ė–ľ “õ“Ī—Ä—č–Ľ—č—Ā—ā–į—Ä ‚ÄĒ –Ņ–ł—Ä–į–ľ–ł–ī–į–Ľ–į—Ä —Ā–į–Ľ–ī—č—Ä“ď–į–Ĺ. –ü–ł—Ä–į–ľ–ł–ī–į —Ā–į–Ľ—É –∂“Ī–ľ—č—Ā—ā–į—Ä—č ”©–Ľ—ą–Ķ—É ”ô–ī—Ė—Ā—ā–Ķ—Ä—Ė–Ĺ –Ī—Ė—Ä—Ā—č–ī—č—Ä“ď—č –∂“Į–Ļ–Ķ–≥–Ķ –ļ–Ķ–Ľ—ā—Ė—Ä–Ķ –ĺ—ā—č—Ä—č–Ņ, –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –ľ–Ķ–Ĺ –ľ–Ķ—Ö–į–Ĺ–ł–ļ–į–Ĺ—č“£ –ī–į–ľ—É—č–Ĺ–į —č“õ–Ņ–į–Ľ –Ķ—ā—ā—Ė. –Ď—Ė–∑–≥–Ķ –∂–Ķ—ā–ļ–Ķ–Ĺ –ľ–į—ā–Ķ–ľ. –Ņ–į–Ņ–ł—Ä—É—Ā—ā–į—Ä –ē–∂–Ķ–Ľ–≥—Ė –ú—č—Ā—č—Ä –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—Ā—č–Ĺ—č“£ –Ī–Ķ—Ä—ā—Ė–Ĺ–≥—Ė “ď–į—Ā—č—Ä–Ľ–į—Ä—č–Ĺ–į –∂–į—ā–į–ī—č. –ü–į–Ņ–ł—Ä—É—Ā—ā–į—Ä–ī–į“ď—č –į—É–ī–į–Ĺ –ľ–Ķ–Ĺ –ļ”©–Ľ–Ķ–ľ –∂”©–Ĺ—Ė–Ĺ–ī–Ķ–≥—Ė –Ķ—Ā–Ķ–Ņ—ā–Ķ—Ä–ī—Ė“£ –ļ”©–Ņ—ą—Ė–Ľ—Ė–≥—Ė –ī“Ī—Ä—č—Ā —ą—č“ď–į—Ä—č–Ľ“ď–į–Ĺ. –Ď—Ė—Ä–į“õ –Ķ—Ä–Ķ–∂–Ķ–Ľ–Ķ—Ä–ī—Ė“£ –Ķ—ą“õ–į–Ļ—Ā—č—Ā—č –ī”ô–Ľ–Ķ–Ľ–ī–Ķ–Ĺ–Ī–Ķ–≥–Ķ–Ĺ. “ģ—ą–Ī“Ī—Ä—č—ą—ā—č“£, —ā—Ä–į–Ņ–Ķ—Ü–ł—Ź–Ĺ—č“£, –ī”©“£–≥–Ķ–Ľ–Ķ–ļ—ā—Ė“£ –į—É–ī–į–Ĺ—č –∂—É—č“õ —ā“Į—Ä–ī–Ķ –Ķ—Ā–Ķ–Ņ—ā–Ķ–Ľ–≥–Ķ–Ĺ, —ā–į–Ī–į–Ĺ–ī–į—Ä—č –ļ–≤–į–ī—Ä–į—ā –Ī–ĺ–Ľ—č–Ņ –ļ–Ķ–Ľ–≥–Ķ–Ĺ “õ–ł—č“õ –Ņ–ł—Ä–į–ľ–ł–ī–į–Ĺ—č“£ –ļ”©–Ľ–Ķ–ľ—Ė –ī”ô–Ľ —ā–į–Ī—č–Ľ“ď–į–Ĺ. –ē–∂–Ķ–Ľ–≥—Ė –í–į–≤–ł–Ľ–ĺ–Ĺ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č–Ĺ—č“£ –ī–Ķ—Ä–Ķ–ļ—ā–Ķ—Ä—Ė –Ī–į–Ľ—ą—č“õ—ā–į–Ĺ –ł–Ľ–Ķ–Ĺ—Ė–Ņ –∂–į—Ā–į–Ľ“ď–į–Ĺ —ā–į“õ—ā–į—ą–į–Ľ–į—Ä“ď–į –∂–į–∑—č–Ľ—č–Ņ “õ–į–Ľ“ď–į–Ĺ. –ě–Ľ–į—Ä“ď–į “õ–į—Ä–į“ď–į–Ĺ–ī–į “Ī–∑—č–Ĺ–ī—č“õ, –į—É–ī–į–Ĺ, –ļ”©–Ľ–Ķ–ľ –∂”©–Ĺ—Ė–Ĺ–ī–Ķ–≥—Ė –ľ—č—Ā—č—Ä–Ľ—č“õ—ā–į—Ä –Ī—Ė–Ľ–≥–Ķ–Ĺ –Ķ—Ā–Ķ–Ņ—ā–Ķ—Ä–ī—Ė –≤–į–≤–ł–Ľ–ĺ–Ĺ–ī—č“õ—ā–į—Ä –ī–į —ą—č“ď–į—Ä–į –Ī—Ė–Ľ–≥–Ķ–Ĺ. –í–į–≤–ł–Ľ–ĺ–Ĺ–ī—č“õ—ā–į—Ä –ļ–Ķ–Ļ–Ī—Ė—Ä –ī“Ī—Ä—č—Ā –ļ”©–Ņ–Ī“Ī—Ä—č—ą—ā–į—Ä–ī—č, “õ–ł—č“õ –ļ–ĺ–Ĺ—É—Ā—ā—č, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į “õ–į—Ä–į—Ā—ā—č—Ä“ď–į–Ĺ, —ą–Ķ“£–Ī–Ķ—Ä–ī—Ė 360 –≥—Ä–į–ī—É—Ā“õ–į –Ī”©–Ľ—É–ī—Ė —ą—č“ď–į—Ä“ď–į–Ĺ, –Ķ—Ā–Ķ–Ņ—ā–Ķ—Ä–ī—Ė —ā–Ķ“£–ī–Ķ—É–Ľ–Ķ—Ä–≥–Ķ –ļ–Ķ–Ľ—ā—Ė—Ä—É–ī—Ė –∂–į“õ—Ā—č –Ī—Ė–Ľ–≥–Ķ–Ĺ, –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č –į—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ–ł—Ź“ď–į “õ–ĺ–Ľ–ī–į–Ĺ–į –Ī–į—Ā—ā–į“ď–į–Ĺ. –í–į–≤–ł–Ľ–ĺ–Ĺ–ī—č“õ—ā–į—Ä“ď–į –ü–ł—Ą–į–≥–ĺ—Ä —ā–Ķ–ĺ—Ä–Ķ–ľ–į—Ā—č –ī–į –Ī–Ķ–Ľ–≥—Ė–Ľ—Ė –Ī–ĺ–Ľ“ď–į–Ĺ. –ö–Ķ–Ļ–Ī—Ė—Ä –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ—č“õ –ī–Ķ—Ä–Ķ–ļ—ā–Ķ—Ä –ē–∂–Ķ–Ľ–≥—Ė “ģ–Ĺ–ī—Ė—Ā—ā–į–Ĺ –ľ–Ķ–Ĺ “ö—č—ā–į–Ļ–ī–į –ī–į –ļ–Ķ–∑–ī–Ķ—Ā–Ķ–ī—Ė. –Ī—Ė–∑–ī—Ė“£ –∑–į–ľ–į–Ĺ—č–ľ—č–∑–ī–į–Ĺ –Ī“Į—Ä—č–Ĺ 7‚ÄĒ6 “ď–į—Ā—č—Ä–Ľ–į—Ä–ī–į –≥—Ä–Ķ–ļ—ā–Ķ—Ä–ī—Ė“£ –į—Ä–į—Ā—č–Ĺ–į–Ĺ “ď—č–Ľ—č–ľ–ľ–Ķ–Ĺ –į—Ä–Ĺ–į–Ļ—č —ą“Ī“ď—č–Ľ–ī–į–Ĺ–į—ā—č–Ĺ, —ā–į–Ī–ł“ď–į—ā “õ“Ī–Ī—č–Ľ—č—Ā—ā–į—Ä—č–Ĺ –∑–Ķ—Ä—ā—ā–Ķ–Ļ—ā—Ė–Ĺ –ĺ“õ—č–ľ—č—Ā—ā—č–Ľ–į—Ä —ą—č“õ—ā—č. –ě–Ľ–į—Ä–ī—č“£ –ļ–Ķ–Ļ–Ī—Ė—Ä–Ķ—É—Ė –Ī—Ė–Ľ—Ė–ľ —Ė–∑–ī–Ķ–Ņ, –Ķ–Ľ –ļ–Ķ–∑—Ė–Ņ, –ļ”©—Ä—ą—Ė —Ö–į–Ľ—č“õ—ā–į—Ä–ī—č“£ —ā“Ī—Ä–ľ—č—Ā—č–ľ–Ķ–Ĺ, “ď—č–Ľ.-–ľ”ô–ī–Ķ–Ĺ–ł —ā–į–Ī—č—Ā—ā–į—Ä—č–ľ–Ķ–Ĺ —ā–į–Ĺ—č—Ā—č–Ņ, —Ā–į—Ź—Ö–į—ā—ā–į—Ä –∂–į—Ā–į–ī—č, –ú—č—Ā—č—Ä –ľ–Ķ–Ĺ –í–į–≤–ł–Ľ–ĺ–Ĺ“ď–į –Ī–į—Ä—č–Ņ –∂“Į—Ä–ī—Ė. ”®–Ĺ–ī—Ė—Ä–≥—Ė—ą –ļ“Į—ą—ā–Ķ—Ä–ī—Ė“£ –ī–į–ľ—É—č, –Ĺ–į“õ—ā—č —Ą–į–ļ—ā—Ė–Ľ–Ķ—Ä–ī—Ė“£ –ľ–ĺ–Ľ–į—é—č, –ĺ“õ—č–ľ—č—Ā—ā—č–Ľ–į—Ä–ī—č“£ –ĺ–Ļ ”©—Ä—Ė—Ā—Ė–Ĺ—Ė“£ ”©—Ā—É—Ė –ľ–į—ā–Ķ–ľ. —Ā”©–Ļ–Ľ–Ķ–ľ–ī–Ķ—Ä–ī—Ė —ā–Ķ–ļ—Ā–Ķ—Ä—É –∂”ô–Ĺ–Ķ –ī”ô–Ľ–Ķ–Ľ–ī–Ķ—É ”ô–ī—Ė—Ā—ā–Ķ—Ä—Ė–Ĺ —ā—É–ī—č—Ä–ī—č. –ú—č—Ā–į–Ľ—č, —Ä–į–ī–ł—É—Ā—č r-–≥–Ķ —ā–Ķ“£ –ī”©“£–≥–Ķ–Ľ–Ķ–ļ—ā—Ė“£ –į—É–ī–į–Ĺ—č–Ĺ –ľ—č—Ā—č—Ä–Ľ—č“õ—ā–į—Ä 256 r2 : 81 –ī–Ķ–Ņ, –≤–į–≤–ł–Ľ–ĺ–Ĺ–ī—č“õ—ā–į—Ä 3 r2 –ī–Ķ–Ņ –Ķ—Ā–Ķ–Ņ—ā–Ķ–≥–Ķ–Ĺ. –ě—Ā—č–Ľ–į—Ä–ī—č“£ –ī“Ī—Ä—č—Ā—č–Ĺ —ā–į“£–ī–į–Ņ –į–Ľ—É “Į—ą—Ė–Ĺ —ā–ł—Ė—Ā—ā—Ė —Ā”©–Ļ–Ľ–Ķ–ľ–ī—Ė ‚ÄĒ —ā–Ķ–ĺ—Ä–Ķ–ľ–į–Ĺ—č –ī”ô–Ľ–Ķ–Ľ–ī–Ķ—É –ļ–Ķ—Ä–Ķ–ļ –Ī–ĺ–Ľ–ī—č. –Ď—Ė—Ä—ā–į–Ľ–į–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ–į–Ľ–į—Ä–ī—č –§–į–Ľ–Ķ—Ā, –ü–ł—Ą–į–≥–ĺ—Ä, –ď–ł–Ņ–Ņ–ĺ–ļ—Ä–į—ā, –Ē–Ķ–ľ–ĺ–ļ—Ä–ł—ā –ī”ô–Ľ–Ķ–Ľ–ī–Ķ–ī—Ė. –Ē”ô–Ľ–Ķ–Ľ-–ī–Ķ–ľ–Ķ–Ľ–Ķ—Ä–ī—Ė“£ –ī“Ī—Ä—č—Ā “õ–į–Ľ—č–Ņ—ā–į—Ā—É—č–Ĺ–į —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą–ł—Ź “ď—č–Ľ—č–ľ—č–Ĺ—č“£ –ī–į —č“õ–Ņ–į–Ľ—č –Ī–ĺ–Ľ–ī—č. –°”©–Ļ—ā—Ė–Ņ, –Ī—Ė–∑–ī—Ė“£ –∑–į–ľ–į–Ĺ—č–ľ—č–∑–ī–į–Ĺ –Ī“Ī—Ä—č–Ĺ 5 “ď–į—Ā—č—Ä–ī–į –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź ”©–∑—Ė–Ĺ–Ķ —ā”ô–Ĺ “Ī“ď—č–ľ–ī–į—Ä—č –ľ–Ķ–Ĺ ”ô–ī—Ė—Ā—ā–Ķ—Ä—Ė –Ī–į—Ä –∂“Į–Ļ–Ķ–Ľ—Ė “ď—č–Ľ—č–ľ –ī”ô—Ä–Ķ–∂–Ķ—Ā—Ė–Ĺ–Ķ –ļ”©—ā–Ķ—Ä—Ė–Ľ–ī—Ė. –ě—Ā—č –ī”ô—É—Ė—Ä–ī—Ė“£ –į—Ź“ď—č–Ĺ–ī–į –ď–ł–Ņ–Ņ–ĺ–ļ—Ä–į—ā, –§–Ķ–ĺ–ī–Ķ—Ā–ł–Ļ, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į ‚Äú–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ĺ–Ķ–≥—Ė–∑–ī–Ķ—Ä—Ė‚ÄĚ –ī–Ķ–≥–Ķ–Ĺ –į—ā–Ņ–Ķ–Ĺ –ļ”©–Ľ–Ķ–ľ–ī—Ė –ļ—Ė—ā–į–Ņ—ā–į—Ä –∂–į–∑–ī—č. –ē–ļ—Ė–Ĺ—ą—Ė –ī”ô—É—Ė—Ä–ī—Ė“£ –Ī–į—Ā—č –Ī–ĺ–Ľ“ď–į–Ĺ –ē–≤–ļ–Ľ–ł–ī –Ķ“£–Ī–Ķ–ļ—ā–Ķ—Ä—Ė —ą—č“õ“õ–į–Ĺ–ī–į –Ī“Ī–Ľ –ļ—Ė—ā–į–Ņ—ā–į—Ä –ļ–Ķ–Ļ—Ė–Ĺ —č—Ā—č—Ä—č–Ľ—č–Ņ, –į“õ—č—Ä—č –ľ“Į–Ľ–ī–Ķ –Ķ—Ā–ļ–Ķ—Ä—É—Ā—Ė–∑ “õ–į–Ľ—č–Ņ “õ–ĺ–Ļ–ī—č.

–ē–ļ—Ė–Ĺ—ą—Ė –ī”ô—É—Ė—Ä ‚ÄĒ –ē–≤–ļ–Ľ–ł–ī—ā–Ķ–Ĺ –†. –Ē–Ķ–ļ–į—Ä—ā“õ–į –ī–Ķ–Ļ—Ė–Ĺ–≥—Ė –ļ–Ķ–∑–Ķ“£; –ĺ–Ľ 2 –ľ—č“£ –∂—č–Ľ“ď–į —Ā–ĺ–∑—č–Ľ–ī—č. –ē–≤–ļ–Ľ–ł–ī –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ ”©–∑—Ė–Ĺ–Ķ –ī–Ķ–Ļ—Ė–Ĺ–≥—Ė —ā–į–Ī—č—Ā—ā–į—Ä—č–Ĺ –∂–ł–Ĺ–į–Ņ, —ā–į–Ľ–ī–į–Ņ, “õ–ĺ—Ä—č—ā—č–Ņ, –Ī—Ė—Ä —Ė–∑–≥–Ķ —ā“Į—Ā—Ė—Ä—Ė–Ņ, –Ī—Ė–∑–ī—Ė“£ –∑–į–ľ–į–Ĺ—č–ľ—č–∑–ī–į–Ĺ –Ī“Ī—Ä—č–Ĺ 300 –∂—č–Ľ—č —ą–į–ľ–į—Ā—č–Ĺ–ī–į ‚Äú–Ě–Ķ–≥—Ė–∑–ī–Ķ—Ä‚ÄĚ –į—ā—ā—č, 13 –Ī”©–Ľ—Ė–ľ–Ĺ–Ķ–Ĺ “õ“Ī—Ä–į–Ľ“ď–į–Ĺ —ą—č“ď–į—Ä–ľ–į –∂–į–∑–ī—č. –ě–Ĺ–ī–į –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –į–ļ—Ā–ł–ĺ–ľ–į–Ľ–į—Ä –ľ–Ķ–Ĺ “õ–į“ď–ł–ī–į–Ľ–į—Ä (–Ņ–ĺ—Ā—ā—É–Ľ–į—ā—ā–į—Ä) –Ĺ–Ķ–≥—Ė–∑—Ė–Ĺ–ī–Ķ –Ľ–ĺ–≥–ł–ļ–į–Ľ—č“õ –∂–ĺ–Ľ–ľ–Ķ–Ĺ “õ“Ī—Ä—č–Ľ“ď–į–Ĺ –∂“Į–Ļ–Ķ–Ľ—Ė –ī–Ķ–ī—É–ļ—ā–ł–≤—ā—Ė–ļ “ď—č–Ľ—č–ľ (–ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ –Ņ—Ė—ą—Ė–Ĺ–ī–Ķ—Ä –ľ–Ķ–Ĺ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —ā—É—Ä–į–Ľ—č “ď—č-–Ľ—č–ľ) –ī”ô—Ä–Ķ–∂–Ķ—Ā—Ė–Ĺ–ī–Ķ –Ī–į—Ź–Ĺ–ī–į–Ľ–ī—č. ‚Äú–Ě–Ķ–≥—Ė–∑–ī–Ķ—Ä–ī–Ķ‚ÄĚ 121 –į–Ĺ—č“õ—ā–į–ľ–į, 5 “õ–į“ď–ł–ī–į, 9 –į–ļ—Ā–ł–ĺ–ľ–į, 373 —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ļ–Ķ–Ľ—ā—Ė—Ä—Ė–Ľ–≥–Ķ–Ĺ. –ě—Ā—č –ļ“Į–Ĺ–≥—Ė —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź, –∂–į–Ľ–Ņ—č –į–Ľ“ď–į–Ĺ–ī–į, –ē–≤–ļ–Ľ–ł–ī “õ–į–Ľ—č–Ī—č–Ĺ–į–Ĺ —ą—č“õ“õ–į–Ĺ. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź“ď–į –ź—Ä—Ö–ł–ľ–Ķ–ī –Ņ–Ķ–Ĺ –ź–Ņ–ĺ–Ľ–Ľ–ĺ–Ĺ–ł–Ļ –ī–Ķ —Ė—Ä—Ė “Į–Ľ–Ķ—Ā “õ–ĺ—Ā—ā—č. –Ď“Ī–Ľ–į—Ä–ī—č“£ –Ī—Ė—Ä—Ė–Ĺ—ą—Ė—Ā—Ė ‚ÄĒ –ī”©“£–≥–Ķ–Ľ–Ķ–ļ—ā—Ė“£, –Ņ–į—Ä–į–Ī–ĺ–Ľ–į —Ā–Ķ–≥–ľ–Ķ–Ĺ—ā—Ė–Ĺ—Ė“£ –į—É–ī–į–Ĺ—č, –Ņ–ł—Ä–į–ľ–ł–ī–į–Ĺ—č“£, –ļ–ĺ–Ĺ—É—Ā—ā—č“£ –∂”ô–Ĺ–Ķ —ą–į—Ä–ī—č“£ –ļ”©–Ľ–Ķ–ľ—Ė –∂”©–Ĺ—Ė–Ĺ–ī–Ķ–≥—Ė —ā–Ķ–ĺ—Ä–Ķ–ľ–į–Ľ–į—Ä–ī—č, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į —ā“Ī–∂—č—Ä—č–ľ–ī–į–ī—č, –į–Ľ –Ķ–ļ—Ė–Ĺ—ą—Ė—Ā—Ė ‚ÄĒ –ļ–ĺ–Ĺ—É—Ā—ā—č“õ “õ–ł–ľ–į–Ľ–į—Ä–ī—č –ľ“Ī“õ–ł—Ź—ā –∑–Ķ—Ä—ā—ā–Ķ–Ņ, “õ“Ī–Ĺ–ī—č “ď—č–Ľ. –ľ“Ī—Ä–į “õ–į–Ľ–ī—č—Ä–ī—č. –ź—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ–ł—Ź–ľ–Ķ–Ĺ —ą“Ī“ď—č–Ľ–ī–į–Ĺ“ď–į–Ĺ ‚ÄĒ –ď–ł–Ņ–Ņ–į—Ä—Ö, –ö. –ü—ā–ĺ–Ľ–Ķ–ľ–Ķ–Ļ, –ú–Ķ–Ĺ–Ķ–Ľ–į–Ļ, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į —Ā—Ą–Ķ—Ä–į–Ľ—č“õ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –ľ–Ķ–Ĺ —ā—Ä–ł–≥–ĺ–Ĺ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č “õ–į–Ľ—č–Ņ—ā–į—Ā—ā—č—Ä–ī—č. –ē–≤–ļ–Ľ–ł–ī, –ź—Ä—Ö–ł–ľ–Ķ–ī, –ź–Ņ–ĺ–Ľ–Ľ–ĺ–Ĺ–ł–Ļ –∑–į–ľ–į–Ĺ—č –≥—Ä–Ķ–ļ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č–Ĺ—č“£ ‚Äú–į–Ľ—ā—č–Ĺ “ď–į—Ā—č—Ä—č‚ÄĚ –Ī–ĺ–Ľ“ď–į–Ĺ –Ķ–ī—Ė. –ě–ī–į–Ĺ –ļ–Ķ–Ļ—Ė–Ĺ –ď—Ä–Ķ–ļ–ł—Ź–Ĺ—č“£ “ď—č–Ľ—č–ľ—č –ľ–Ķ–Ĺ –ľ”ô–ī–Ķ–Ĺ–ł–Ķ—ā—Ė “õ“Ī–Ľ–ī—č—Ä–į–Ļ –Ī–į—Ā—ā–į–ī—č. –ě—Ä—ā–į “ď–į—Ā—č—Ä–Ľ–į—Ä–ī–į —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź “ģ–Ĺ–ī—Ė—Ā—ā–į–Ĺ–ī–į, –ě—Ä—ā–į –ź–∑–ł—Ź–ī–į, –į—Ä–į–Ī –Ķ–Ľ–ī–Ķ—Ä—Ė–Ĺ–ī–Ķ –ī–į–ľ—č–ī—č. –ě—Ä—ā–į –ź–∑–ł—Ź –ľ–Ķ–Ĺ “ö–į–∑–į“õ—Ā—ā–į–Ĺ –ĺ“õ—č–ľ—č—Ā—ā—č–Ľ–į—Ä—č–Ĺ–į–Ĺ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–ľ–Ķ–Ĺ —ą“Ī“ď—č–Ľ–ī–į–Ĺ“ď–į–Ĺ–ī–į—Ä: “í–į–Ī–Ī–į—Ā ”ô–Ľ-–Ė–į—É—ó–į—Ä–ł, ”ė–Ī—É –Ě–į—Ā—Ä ”ô–Ľ-–§–į—Ä–į–Ī–ł, ”ė–Ī—É –†–į–Ļ—Ö–į–Ĺ ”ô–Ľ-–Ď–ł—Ä—É–Ĺ–ł, “í–ł–Ļ–į—Ā ”ô–ī-–Ē–ł–Ĺ –Ė”ô–ľ—ą–ł–ī ”ô–Ľ-–ö”ô—ą–ł, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į –Ī–ĺ–Ľ–ī—č. –ē–ļ—Ė–Ĺ—ą—Ė –ī”ô—É—Ė—Ä–ī—Ė“£ –į—Ź“ď—č–Ĺ–ī–į –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ď–į—ā—č—Ā –ē—É—Ä–ĺ–Ņ–į–ī–į –∂–į–Ĺ–ī–į–Ĺ–į –Ī–į—Ā—ā–į–ī—č. –Ď“Ī–Ľ –ļ–Ķ–∑–ī–Ķ –ė. –ö–Ķ–Ņ–Ľ–Ķ—Ä –ľ–Ķ–Ĺ –ł—ā–į–Ľ—Ć—Ź–Ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –Ď. –ö–į–≤–į–Ľ—Ć–Ķ—Ä–ł–ī—Ė“£ (1598 ‚ÄĒ 1647) –Ķ“£–Ī–Ķ–ļ—ā–Ķ—Ä—Ė —ā–į—Ä–ł—Ö–ł –Ī–Ķ–Ľ–Ķ—Ā –Ī–ĺ–Ľ–ī—č.
“ģ—ą—Ė–Ĺ—ą—Ė –ī”ô—É—Ė—Ä –†. –Ē–Ķ–ļ–į—Ä—ā—ā–į–Ĺ –Ě.–ė. –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ–≥–Ķ –ī–Ķ–Ļ—Ė–Ĺ–≥—Ė 200 –∂—č–Ľ–ī—č “õ–į–ľ—ā–ł–ī—č. –Ď“Ī–Ľ –ī”ô—É—Ė—Ä–ī–Ķ –į–Ĺ–į–Ľ–ł—ā., –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤—ā—Ė–ļ –∂”ô–Ĺ–Ķ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ī—č“õ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ–į—Ä –Ņ–į–Ļ–ī–į –Ī–ĺ–Ľ–ī—č. –ź–Ĺ–į–Ľ–ł—ā–ł–ļ–į–Ľ—č“õ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—ā–į—Ä ”ô–ī—Ė—Ā—Ė–Ĺ–Ķ —Ā“Į–Ļ–Ķ–Ĺ–Ķ–ī—Ė. –ě–Ĺ–ī–į –Ĺ“Į–ļ—ā–Ķ–Ĺ—Ė“£ –ĺ—Ä–Ĺ—č —Ā–į–Ĺ–ī–į—Ä –į—Ä“õ—č–Ľ—č, –į–Ľ —Ā—č–∑—č“õ—ā–į—Ä –ľ–Ķ–Ĺ –Ī–Ķ—ā—ā–Ķ—Ä —ā–Ķ“£–ī–Ķ—É–Ľ–Ķ—Ä –į—Ä“õ—č–Ľ—č –į–Ĺ—č“õ—ā–į–Ľ–į–ī—č. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –Ī“Ī–Ľ —Ā–į–Ľ–į—Ā—č–Ĺ—č“£ —Ė—Ä–≥–Ķ—Ā—Ė–Ĺ –Ē–Ķ–ļ–į—Ä—ā –Ņ–Ķ–Ĺ —Ą—Ä–į–Ĺ—Ü—É–∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –ü. –§–Ķ—Ä–ľ–į (1601 ‚ÄĒ 65) “õ–į–Ľ–į–ī—č, –į–Ľ –ĺ–Ĺ—č —Ą—Ä–į–Ĺ—Ü—É–∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –ź. –ö–Ľ–Ķ—Ä–ĺ (1713 ‚ÄĒ 65) –ľ–Ķ–Ĺ –õ. –≠–Ļ–Ľ–Ķ—Ä –ļ–Ķ–ľ–Ķ–Ľ–ī–Ķ–Ĺ–ī—Ė—Ä–ī—Ė. –§–ł–≥—É—Ä–į–Ľ–į—Ä–ī—č –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź–Ľ–į—Ä –į—Ä“õ—č–Ľ—č —ā“Į—Ä–Ľ–Ķ–Ĺ–ī—Ė—Ä—É –∂–ĺ–Ľ–ī–į—Ä—č–Ĺ –∑–Ķ—Ä—ā—ā–Ķ—É –Ĺ”ô—ā–ł–∂–Ķ—Ā—Ė–Ĺ–ī–Ķ –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤—ā—Ė–ļ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź “õ–į–Ľ—č–Ņ—ā–į—Ā—ā—č. –Ď“Ī–Ľ –Ī–į“ď—č—ā—ā–į —Ą—Ä–į–Ĺ—Ü—É–∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –Ė. –Ē–Ķ–∑–į—Ä–≥ (1593 ‚ÄĒ 1662), –Ď. –ü–į—Ā–ļ–į–Ľ—Ć, —Ą—Ä–į–Ĺ—Ü—É–∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –Ė. –ü–ĺ–Ĺ—Ā–Ķ–Ľ–Ķ (1788 ‚ÄĒ 1867), –Ĺ–Ķ–ľ—Ė—Ā –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –ö. –®—ā–į—É–ī—ā (1798 ‚ÄĒ 1867), —ą–≤–Ķ–Ļ—Ü–į—Ä –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –Į. –®—ā–Ķ–Ļ–Ĺ–Ķ—Ä (1796 ‚ÄĒ 1863) –∂–Ķ–ľ—Ė—Ā—ā—Ė –Ķ“£–Ī–Ķ–ļ –Ķ—ā—ā—Ė. –ö–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ–≥—Ė —Ą–ł–≥—É—Ä–į–Ĺ—č –∂–į–∑—č“õ—ā—č“õ—ā–į –ļ–Ķ—Ā–ļ—Ė–Ĺ–ī–Ķ—É –∂–ĺ–Ľ–ī–į—Ä—č–Ĺ —ā–į–Ľ–ī–į–Ņ, —Ą—Ä–į–Ĺ—Ü—É–∑ –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –ď. –ú–ĺ–Ĺ–∂ (1746 ‚ÄĒ 1811) —Ā—č–∑–Ī–į –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č –∂–į—Ā–į–ī—č. –°—č–∑–Ī–į –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤—ā—Ė–ļ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ —ā–į—Ä–į—É—č –Ī–ĺ–Ľ—č–Ņ —Ā–į–Ĺ–į–Ľ–į–ī—č. –≠–Ļ–Ľ–Ķ—Ä –ľ–Ķ–Ĺ –ú–ĺ–Ĺ–∂ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ī—č“õ –Ķ—Ā–Ķ–Ņ—ā–Ķ—É ”ô–ī—Ė—Ā—ā–Ķ—Ä—Ė–Ĺ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź“ď–į “õ–ĺ–Ľ–ī–į–Ĺ–į –Ī–į—Ā—ā–į“ď–į–Ĺ –Ī–ĺ–Ľ–į—ā—č–Ĺ. –ö. –ď–į—É—Ā—Ā –Ī“Ī–Ľ –ľ”ô—Ā–Ķ–Ľ–Ķ–Ĺ—Ė –ĺ–ī–į–Ĺ ”ô—Ä—Ė –ī–į–ľ—č—ā—č–Ņ, –ļ–Ľ–į—Ā—Ā–ł–ļ–į–Ľ—č“õ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ī—č“õ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č “õ–į–Ľ—č–Ņ—ā–į—Ā—ā—č—Ä–ī—č. –Ē–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ī—č“õ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —Ā—č–∑—č“õ—ā–į—Ä –ľ–Ķ–Ĺ –Ī–Ķ—ā—ā–Ķ—Ä–ī—Ė“£ “õ–į—Ā–ł–Ķ—ā—ā–Ķ—Ä—Ė–Ĺ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ī–į—Ä –į—Ä“õ—č–Ľ—č –∑–Ķ—Ä—ā—ā–Ķ–Ļ–ī—Ė.
–Ę”©—Ä—ā—Ė–Ĺ—ą—Ė –ī”ô—É—Ė—Ä –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ –Ķ“£–Ī–Ķ–ļ—ā–Ķ—Ä—Ė–Ĺ–Ķ–Ĺ –Ī–į—Ā—ā–į–Ľ–į–ī—č. ”®–∑ –∑–Ķ—Ä—ā—ā–Ķ—É–Ľ–Ķ—Ä—Ė–Ĺ–ī–Ķ –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ “Į—ą –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ļ–Ķ —Ā“Į–Ļ–Ķ–Ĺ–ī—Ė. –ě–Ľ–į—Ä: –ē–≤–ļ–Ľ–ł–ī –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č –Ī–ĺ–Ľ—É“ď–į —ā–ł—Ė—Ā –∂”ô–Ĺ–Ķ –ĺ–Ľ –Ī—Ė—Ä–ī–Ķ–Ĺ-–Ī—Ė—Ä –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ķ–ľ–Ķ—Ā; –į–ļ—Ā–ł–ĺ–ľ–į–Ľ–į—Ä–ī—č ”©–∑–≥–Ķ—Ä—ā—Ė–Ņ, –∂–į“£–į –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–∂–į—Ā–į—É“ď–į –Ī–ĺ–Ľ–į–ī—č; –Ĺ–į“õ—ā—č –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ–ļ–Ķ “õ–į–Ĺ–ī–į–Ļ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —Ā”ô–Ļ–ļ–Ķ—Ā –ļ–Ķ–Ľ–Ķ—ā—Ė–Ĺ–ī—Ė–≥—Ė–Ĺ —ā”ô–∂—Ė—Ä–ł–Ī–Ķ –ļ”©—Ä—Ā–Ķ—ā–Ķ–ī—Ė. –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ –ē–≤–ļ–Ľ–ł–ī—ā—Ė“£ 5-“õ–į“ď–ł–ī–į—Ā—č–Ĺ (–Ņ–ĺ—Ā—ā—É–Ľ–į—ā—č–Ĺ) ”©–∑—Ė–Ĺ—Ė“£ –Ī–į—Ā“õ–į –į–ļ—Ā–ł–ĺ–ľ–į—Ā—č–ľ–Ķ–Ĺ (–õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ –į–ļ—Ā–ł–ĺ–ľ–į—Ā—č –ī–Ķ–Ņ –į—ā–į–Ľ–į—ā—č–Ĺ) –į—É—č—Ā—ā—č—Ä—č–Ņ, –∂–į“£–į –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –∂–į—Ā–į–ī—č. –Ď“Ī–Ľ –ď-“ď–į –ď–į—É—Ā—Ā –Ņ–Ķ–Ĺ –≤–Ķ–Ĺ–≥—Ä –ľ–į—ā–Ķ–ľ–į—ā–ł–≥—Ė –Į. –Ď–ĺ–Ľ—Ć—Ź–Ļ (1802 ‚ÄĒ 60) –ī–į –∂–į“õ—č–Ĺ –ļ–Ķ–Ľ–ī—Ė. 5-“õ–į“ď–ł–ī–į –ĺ—Ä–Ĺ—č–Ĺ–į ”©–∑ –į–ļ—Ā–ł–ĺ–ľ–į—Ā—č–Ĺ (–†–ł–ľ–į–Ĺ –į–ļ—Ā–ł–ĺ–ľ–į—Ā—č –ī–Ķ–Ņ –į—ā–į–Ľ–į—ā—č–Ĺ) –į–Ľ—č–Ņ, –§.–Ď. –†–ł–ľ–į–Ĺ —ć–Ľ–Ľ–ł–Ņ—Ā—ā—Ė–ļ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –Ĺ–Ķ–≥—Ė–∑—Ė–Ĺ —Ā–į–Ľ–ī—č. –†–ł–ľ–į–Ĺ –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė –ļ–Ķ–∑ –ļ–Ķ–Ľ–≥–Ķ–Ĺ –Ī—Ė—Ä—ā–Ķ–ļ—ā–Ķ—Ā –ĺ–Ī—ä–Ķ–ļ—ā—Ė–Ľ–Ķ—Ä –ľ–Ķ–Ĺ “õ“Ī–Ī—č–Ľ—č—Ā—ā–į—Ä–ī—č“£ “Į–∑–ī—Ė–ļ—Ā—Ė–∑ –∂–ł—č–Ĺ—č —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ —ā“Į—Ā—Ė–Ĺ—É “õ–į–∂–Ķ—ā—ā—Ė–≥—Ė–Ĺ –ļ”©—Ä—Ā–Ķ—ā—ā—Ė. –Ď“Ī–Ľ –ł–ī–Ķ—Ź–Ĺ—č“£ “õ“Ī–Ľ–į—ą—č –ļ–Ķ“£ –Ī–ĺ–Ľ–ī—č. –°–ĺ–Ĺ—č“£ –į—Ä“õ–į—Ā—č–Ĺ–ī–į –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė“£ –ļ”©–Ņ—ā–Ķ–≥–Ķ–Ĺ –ľ–į—ā–Ķ–ľ. —ā–Ķ–ĺ—Ä–ł—Ź–Ľ–į—Ä—č –∂–į—Ā–į–Ľ–ī—č. –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ –ł–ī–Ķ—Ź–Ľ–į—Ä—č –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ĺ–Ķ–≥—Ė–∑–ī–Ķ–ľ–Ķ–Ľ–Ķ—Ä—Ė–Ĺ—Ė“£ —ą—č“ď—É—č–Ĺ–į, –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ–į—Ä–ī—č“£ –∂–į–Ľ–Ņ—č–Ľ–į–Ĺ—É—č–Ĺ–į –∂”ô–Ĺ–Ķ –ĺ–Ľ–į—Ä–ī—č“£ –ĺ–ī–į–Ĺ ”ô—Ä—Ė –ī–į–ľ—É—č–Ĺ–į –∂–ĺ–Ľ –į—ą—ā—č. –ü—Ä–ĺ–Ķ–ļ—ā–ł–≤—ā—Ė–ļ-–ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ī—č“õ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź, —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź, –ļ”©–Ņ ”©–Ľ—ą–Ķ–ľ–ī—Ė –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ—Ä –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č, –ļ”©–Ņ–Ī–Ķ–Ļ–Ĺ–Ķ–Ľ—Ė–ļ—ā–Ķ—Ä –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į –ĺ—Ā—č –ī”ô—É—Ė—Ä–ī–Ķ —ą—č“õ—ā—č. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ–į—Ä –Ī—Ė—Ä“õ–į—ā–į—Ä –į—Ä–Ĺ–į—É–Ľ—č —Ā–į–Ľ–į–Ľ–į—Ä“ď–į –Ī”©–Ľ—Ė–Ĺ—Ė–Ņ –ļ–Ķ—ā—ā—Ė.
  
|
| –†–Ķ–Ĺ–Ķ –Ē–Ķ–ļ–į—Ä—ā, –≠–≤–ļ–Ľ–ł–ī, –Ě.–ė.–õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ
|
“ö–į–∑—Ė—Ä–≥—Ė –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź, –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ –Ņ–Ķ–Ĺ —Ą–ł–≥—É—Ä–į–Ĺ—č –∂–ł—č–Ĺ “Ī“ď—č–ľ—č –į—Ä“õ—č–Ľ—č –į–Ĺ—č“õ—ā–į–Ļ–ī—č. –ě–Ĺ–ī–į –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ ”ô–ī–Ķ—ā—ā–Ķ–≥—Ė “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —Ā–ł—Ź“õ—ā—č, –ī”ô–Ļ–Ķ–ļ—ā—Ė “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —ā–į“ď–į–Ļ—č–Ĺ–ī–į–Ľ“ď–į–Ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā—ā–Ķ—Ä–ī—Ė“£ (‚Äú–Ĺ“Į–ļ—ā–Ķ–Ľ–Ķ—Ä–ī—Ė“£‚ÄĚ) –∂–ł—č–Ĺ—č —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ “õ–į—Ä–į—Ā—ā—č—Ä—č–Ľ–į–ī—č. –Ę–ł—Ė—Ā—ā—Ė “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —ā–į“ď–į–Ļ—č–Ĺ–ī–į–Ľ“ď–į–Ĺ –∂–į“ď–ī–į–Ļ–ī–į, —Ā”ô—É–Ľ–Ķ —ā“Į—Ā—ā–Ķ—Ä—Ė–Ĺ—Ė“£ –∂–ł—č–Ĺ—č, [0; 1] –ļ–Ķ—Ā—Ė–Ĺ–ī—Ė—Ā—Ė–Ĺ–ī–Ķ–≥—Ė “Į–∑–ī—Ė–ļ—Ā—Ė–∑ —Ą—É–Ĺ–ļ—Ü–ł—Ź–Ľ–į—Ä–ī—č“£ –∂–ł—č–Ĺ—č, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į ‚Äú–ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ—Ä‚ÄĚ “õ“Ī—Ä–į—Ā—ā—č—Ä–į –į–Ľ–į–ī—č. –°”ô—É–Ľ–Ķ —ā“Į—Ā—ā–Ķ—Ä—Ė, –ļ“Į–Ļ–Ľ–Ķ—Ä, —Ą—É–Ĺ–ļ—Ü–ł—Ź–Ľ–į—Ä —Ā–ĺ–Ľ —Ā”ô–Ļ–ļ–Ķ—Ā ‚Äú–ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ—Ä–ī—Ė“£‚ÄĚ ‚Äú–Ĺ“Į–ļ—ā–Ķ–Ľ–Ķ—Ä—Ė‚ÄĚ —Ä”©–Ľ—Ė–Ĺ –į—ā“õ–į—Ä–į–ī—č. –Ě–Ķ–≥—Ė–∑–≥—Ė –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ ‚Äú–į—Ä–į “õ–į—ą—č“õ—ā—č“õ‚ÄĚ, ‚Äú—Ė–Ľ—Ė–ļ—ā–Ķ—Ā—ā—Ė–ļ‚ÄĚ, ‚Äú–Ĺ“Į–ļ—ā–Ķ –į–Ļ–ľ–į“ď—č‚ÄĚ, ‚Äú—Ā”ô–Ļ–ļ–Ķ—Ā—ā—Ė–ļ‚ÄĚ, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į “Ī“ď—č–ľ–ī–į—Ä –į–Ľ—č–Ĺ–į–ī—č. –Ė–ł—č–Ĺ–ī–į—Ä –ľ–Ķ–Ĺ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä–ī—č ”ô—Ä —ā“Į—Ä–Ľ—Ė –Ķ—ā—Ė–Ņ –į–Ľ—č–Ņ, ”ô—Ä —ā“Į—Ä–Ľ—Ė –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ–į—Ä–ī—č “õ“Ī—Ä–į—Ā—ā—č—Ä—É“ď–į –Ī–ĺ–Ľ–į–ī—č. –°–ĺ“£“ď—č –ļ–Ķ–∑–ī–Ķ ”©–Ľ—ą–Ķ–ľ–ī–Ķ—Ä—Ė–Ĺ—Ė“£ —Ā–į–Ĺ—č —ą–Ķ–ļ—ā–Ķ—É–Ľ—Ė –Ī–ĺ–Ľ–į—ā—č–Ĺ –ļ–Ķ“£—Ė—Ā-—ā—Ė–ļ—ā—Ė“£ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č “õ–į–Ľ—č–Ņ—ā–į—Ā—ā—č. –ě–Ľ —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ–ī—č“õ –į–Ĺ–į–Ľ–ł–∑ –ļ—É—Ä—Ā—č–Ĺ–ī–į –Ī–į—Ź–Ĺ–ī–į–Ľ–į–ī—č.
“ö–į–∑—Ė—Ä–≥—Ė –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź, –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ –Ņ–Ķ–Ĺ —Ą–ł–≥—É—Ä–į–Ĺ—č –∂–ł—č–Ĺ “Ī“ď—č–ľ—č –į—Ä“õ—č–Ľ—č –į–Ĺ—č“õ—ā–į–Ļ–ī—č. –ě–Ĺ–ī–į –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ ”ô–ī–Ķ—ā—ā–Ķ–≥—Ė “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —Ā–ł—Ź“õ—ā—č, –ī”ô–Ļ–Ķ–ļ—ā—Ė “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —ā–į“ď–į–Ļ—č–Ĺ–ī–į–Ľ“ď–į–Ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā—ā–Ķ—Ä–ī—Ė“£ (‚Äú–Ĺ“Į–ļ—ā–Ķ–Ľ–Ķ—Ä–ī—Ė“£‚ÄĚ) –∂–ł—č–Ĺ—č —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ “õ–į—Ä–į—Ā—ā—č—Ä—č–Ľ–į–ī—č. –Ę–ł—Ė—Ā—ā—Ė “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —ā–į“ď–į–Ļ—č–Ĺ–ī–į–Ľ“ď–į–Ĺ –∂–į“ď–ī–į–Ļ–ī–į, —Ā”ô—É–Ľ–Ķ —ā“Į—Ā—ā–Ķ—Ä—Ė–Ĺ—Ė“£ –∂–ł—č–Ĺ—č, [0; 1] –ļ–Ķ—Ā—Ė–Ĺ–ī—Ė—Ā—Ė–Ĺ–ī–Ķ–≥—Ė “Į–∑–ī—Ė–ļ—Ā—Ė–∑ —Ą—É–Ĺ–ļ—Ü–ł—Ź–Ľ–į—Ä–ī—č“£ –∂–ł—č–Ĺ—č, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į ‚Äú–ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ—Ä‚ÄĚ “õ“Ī—Ä–į—Ā—ā—č—Ä–į –į–Ľ–į–ī—č. –°”ô—É–Ľ–Ķ —ā“Į—Ā—ā–Ķ—Ä—Ė, –ļ“Į–Ļ–Ľ–Ķ—Ä, —Ą—É–Ĺ–ļ—Ü–ł—Ź–Ľ–į—Ä —Ā–ĺ–Ľ —Ā”ô–Ļ–ļ–Ķ—Ā ‚Äú–ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ—Ä–ī—Ė“£‚ÄĚ ‚Äú–Ĺ“Į–ļ—ā–Ķ–Ľ–Ķ—Ä—Ė‚ÄĚ —Ä”©–Ľ—Ė–Ĺ –į—ā“õ–į—Ä–į–ī—č. –Ě–Ķ–≥—Ė–∑–≥—Ė –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā—Ė–ļ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ ‚Äú–į—Ä–į “õ–į—ą—č“õ—ā—č“õ‚ÄĚ, ‚Äú—Ė–Ľ—Ė–ļ—ā–Ķ—Ā—ā—Ė–ļ‚ÄĚ, ‚Äú–Ĺ“Į–ļ—ā–Ķ –į–Ļ–ľ–į“ď—č‚ÄĚ, ‚Äú—Ā”ô–Ļ–ļ–Ķ—Ā—ā—Ė–ļ‚ÄĚ, —ā–į“ď—č–ī–į –Ī–į—Ā“õ–į “Ī“ď—č–ľ–ī–į—Ä –į–Ľ—č–Ĺ–į–ī—č. –Ė–ł—č–Ĺ–ī–į—Ä –ľ–Ķ–Ĺ “õ–į—ā—č–Ĺ–į—Ā—ā–į—Ä–ī—č ”ô—Ä —ā“Į—Ä–Ľ—Ė –Ķ—ā—Ė–Ņ –į–Ľ—č–Ņ, ”ô—Ä —ā“Į—Ä–Ľ—Ė –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ľ–į—Ä–ī—č “õ“Ī—Ä–į—Ā—ā—č—Ä—É“ď–į –Ī–ĺ–Ľ–į–ī—č. –°–ĺ“£“ď—č –ļ–Ķ–∑–ī–Ķ ”©–Ľ—ą–Ķ–ľ–ī–Ķ—Ä—Ė–Ĺ—Ė“£ —Ā–į–Ĺ—č —ą–Ķ–ļ—ā–Ķ—É–Ľ—Ė –Ī–ĺ–Ľ–į—ā—č–Ĺ –ļ–Ķ“£—Ė—Ā-—ā—Ė–ļ—ā—Ė“£ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č “õ–į–Ľ—č–Ņ—ā–į—Ā—ā—č. –ě–Ľ —Ą—É–Ĺ–ļ—Ü–ł–ĺ–Ĺ–į–Ľ–ī—č“õ –į–Ĺ–į–Ľ–ł–∑ –ļ—É—Ä—Ā—č–Ĺ–ī–į –Ī–į—Ź–Ĺ–ī–į–Ľ–į–ī—č.
“ö–į–∑–į“õ—Ā—ā–į–Ĺ–ī–į“ď—č –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź “ď—č–Ľ—č–ľ—č–Ĺ—č“£ –∑–Ķ—Ä—ā—ā–Ķ—É –∂“Ī–ľ—č—Ā—ā–į—Ä—č
“ö–į–∑–į“õ—Ā—ā–į–Ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ—ā–Ķ—Ä—Ė–Ĺ—Ė“£ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–ī–į–Ĺ –∂“Į—Ä–≥—Ė–∑–≥–Ķ–Ĺ –∑–Ķ—Ä—ā—ā–Ķ—É –∂“Ī–ľ—č—Ā—ā–į—Ä—č (“ö–į–∑–ú–£-–ī–Ķ 1950 –∂—č–Ľ–ī–į—Ä—č) –į–ļ–į–ī. –ź.–Ē. –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī—Ä–ĺ–≤—ā—č“£ —č“õ–Ņ–į–Ľ—č–Ĺ–į –Ī–į–Ļ–Ľ–į–Ĺ—č—Ā—ā—č –Ī–ĺ–Ľ–ī—č. –ě–Ľ –Ī–Ķ—ā—ā–Ķ—Ä —ā–Ķ–ĺ—Ä–ł—Ź—Ā—č–Ĺ ”ô—Ä—Ė “õ–į—Ä–į–Ļ –ī–į–ľ—č—ā—É –ľ”ô—Ā–Ķ–Ľ–Ķ—Ā—Ė–Ĺ “õ–ĺ–Ļ–ī—č. –°”©–Ļ—ā—Ė–Ņ –Ī–Ķ—ā—ā–Ķ—Ä–ī—Ė“£ –ļ–Ķ“£ –ļ–Ľ–į—Ā—č–Ĺ –Ķ–ļ—Ė –ī”©“£–Ķ—Ā –Ī–Ķ—ā—ā—Ė“£ –į–Ļ—č—Ä–ľ–į—Ā—č —Ä–Ķ—ā—Ė–Ĺ–ī–Ķ “õ–į—Ä–į—Ā—ā—č—Ä—É“ď–į –Ī–ĺ–Ľ–į—ā—č–Ĺ—č–Ĺ –ļ”©—Ä—Ā–Ķ—ā—ā—Ė. –í.–í. –°—ā—Ä–Ķ–Ľ—Ć—Ü–ĺ–≤—ā—č“£ –Ķ“£–Ī–Ķ–ļ—ā–Ķ—Ä—Ė –Ī–Ķ—ā—ā–Ķ—Ä–ī—Ė“£ –∂–į–Ľ–Ņ—č —ā–Ķ–ĺ—Ä–ł—Ź—Ā—č–Ĺ–į –į—Ä–Ĺ–į–Ľ–ī—č. –Ē.–®. –ģ—Ā—É–Ņ–ĺ–≤—ā—č“£ –∑–Ķ—Ä—ā—ā–Ķ—É –∂“Ī–ľ—č—Ā—ā–į—Ä—č –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ –∂”ô–Ĺ–Ķ —ć–ļ–≤–ł–į—Ą—Ą–ł–Ĺ–ī—Ė–ļ –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ—Ä–ī–Ķ —ą–Ķ–ļ—ā—Ė –Ī“Ī—Ä—č–Ľ—č—Ā—č –∂”ô–Ĺ–Ķ —ą–Ķ–ļ—ā—Ė —ā–ĺ–Ľ—č“õ –Ī“Ī—Ä–į–Ľ—É—č –Ī–į—Ä —Ä–Ķ—ā—ā–Ķ–Ľ–ľ–Ķ–≥–Ķ–Ĺ —Ā—č–∑—č“õ—ā–į—Ä–ī—č“£ –∂–į–Ľ–Ņ—č —ā–Ķ–ĺ—Ä–ł—Ź—Ā—č–Ĺ–į –Ī–į–Ļ–Ľ–į–Ĺ—č—Ā—ā—č –Ī–ĺ–Ľ–ī—č. –ö.–ü. –ü–Ķ—Ä—Ā–ł–ī—Ā–ļ–ł–Ļ ”©–∑ –Ķ“£–Ī–Ķ–≥—Ė–Ĺ–ī–Ķ –ē–≤–ļ–Ľ–ł–ī –ļ–Ķ“£—Ė—Ā—ā—Ė–≥—Ė–Ĺ–ī–Ķ–≥—Ė –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č–Ĺ—č“£ —ā“Į—Ā—Ė–Ĺ–ī—Ė—Ä–ľ–Ķ—Ā—Ė–Ĺ –Ī–Ķ—Ä–ī—Ė. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –Ī–į—Ā“õ–į –Ī”©–Ľ—Ė–ľ–ī–Ķ—Ä—Ė–Ĺ–Ķ –∂–į—ā–į—ā—č–Ĺ –∂“Ī–ľ—č—Ā—ā–į—Ä–ī–į–Ĺ: –∂–į–Ľ–Ņ—č –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ľ–į—Ä—č –ď–ł—ą–į—Ä –ļ–ĺ–Ĺ–≥—Ä—É—ć–Ĺ—Ü–ł—Ź—Ā—č –Ī–ĺ–Ľ–į—ā—č–Ĺ “õ–į–Ī–į—ā—ā–į—Ā “õ–ĺ—Ā –ļ–ĺ–Ĺ–≥—Ä—É—ć–Ĺ—Ü–ł—Ź–Ľ–į—Ä –∑–Ķ—Ä—ā—ā–Ķ–Ľ–ī—Ė (–ź.–Ě”ô—É–Ī–Ķ—ā–ĺ–≤); –į—Ą—Ą–ł–Ĺ–ī—Ė–ļ –Ī–į–Ļ–Ľ–į–Ĺ—č—Ā—ā–į“ď—č —Ā—č–∑—č“õ—ā—č“õ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā—ā–Ķ—Ä –ļ–Ķ“£—Ė—Ā—ā—Ė–≥—Ė–Ĺ–ī–Ķ –Ĺ–ĺ—Ä–ľ–į–Ľ—Ć –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—ā–į—Ä–ī—č“£ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ī–į–Ĺ—É —ā”ô—Ä—ā—Ė–Ī—Ė “õ–į—Ä–į—Ā—ā—č—Ä—č–Ľ–ī—č (–≠.–ė. –•–ľ–Ķ–Ľ–Ķ–≤—Ā–ļ–ł–Ļ); –ļ–Ķ“£—Ė—Ā—ā—Ė–ļ—ā–Ķ–≥—Ė —ā”©—Ä—ā-“Ī–Ľ–Ņ–į “õ–ł—Ā—č“õ—ā—č“£ 11 —ā“Į—Ä—Ė —ā–į–Ī—č–Ľ–ī—č (–Ę.–ö. –Ě”ô–∑—Ė—Ä–ĺ–≤); –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ –∂–į–∑—č“õ—ā—č“ď—č–Ĺ–ī–į —ā–ĺ—Ä –Ī“Ī—Ä—č—ą—č–ľ–Ķ–Ĺ –į–Ĺ—č“õ—ā–į–Ľ–ľ–į–Ļ—ā—č–Ĺ —ā“Į–∑—É —Ā—č–∑—č“õ—ā—č —ā–ĺ—Ä–Ľ–į—Ä–ī—č“£ “õ–į—Ā–ł–Ķ—ā—ā–Ķ—Ä—Ė –∑–Ķ—Ä—ā—ā–Ķ–Ľ–ī—Ė (–ü.–ė.–Ę–ĺ–ļ–į—Ä–Ķ–≤); —ą–Ķ–ļ–į—Ä–į–Ľ–į—Ä—č–Ĺ–ī–į –Ī–į–Ļ–Ľ–į–Ĺ—č—Ā—ā–į—Ä—č –Ī–į—Ä “õ–ł—Ā—č“õ—ā—č“ď—č —ā–Ķ—Ä—Ė—Ā –į–Ļ–Ĺ–į–Ľ—É –Ī–Ķ—ā—ā–Ķ—Ä—Ė–Ĺ—Ė“£ —ą–Ķ–ļ—Ā—Ė–∑ –į–∑ –ł—Ė–Ľ—Ė–ľ—Ė “õ–į—Ä–į—Ā—ā—č—Ä—č–Ľ–ī—č (–Ė. ”®—ā–Ķ—É–Ľ–ł–Ķ–≤); –Ī—Ė—Ä“õ–į—ā–į—Ä –∂“Ī–ľ—č—Ā—ā–į—Ä –≤–Ķ–ļ—ā–ĺ—Ä–Ľ—č“õ –Ķ—Ā–Ķ–Ņ—ā–Ķ—É-–Ľ–Ķ—Ä–ī—Ė“£ —ą—č“ď—É —ā–į—Ä–ł—Ö—č –ľ–Ķ–Ĺ –∂–Ķ–ļ–Ķ –ī–į–ľ—É—č–Ĺ–į –į—Ä–Ĺ–į–Ľ–ī—č (–§.–Ē. –ö—Ä–į–ľ–į—Ä).[2]
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —ā“Į—Ä–Ľ–Ķ—Ä—Ė
–§–Ķ–Ľ–ł–ļ—Ā –ö–Ľ–Ķ–Ļ–Ĺ 1872 –∂—č–Ľ—č –≠—Ä–Ľ–į–Ĺ–≥–Ķ–Ĺ –Ņ—Ä–ĺ–≥—Ä–į–ľ–ľ–į—Ā—č–Ĺ–ī–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —ā“Į—Ä–Ľ–Ķ—Ä—Ė–Ĺ –į–Ľ“ď–į—ą“õ—č —Ä–Ķ—ā –∑–Ķ—Ä—ā—ā–Ķ—É –Ĺ—č—Ā–į–Ĺ–ī–į—Ä—č–Ĺ–į –Ī–į–Ļ–Ľ–į–Ĺ—č—Ā—ā—č –∑–Ķ—Ä—ā—ā–Ķ–≥–Ķ–Ĺ. –ě—Ā—č“ď–į–Ĺ –Ī–į–Ļ–Ľ–į–Ĺ—č—Ā—ā—č –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –ļ–Ķ–Ľ–Ķ—Ā—Ė —ā“Į—Ä–Ľ–Ķ—Ä—Ė –į–Ļ“õ—č–Ĺ–ī–į–Ľ–į–ī—č:
 –°—Ą–Ķ—Ä–į–Ľ—č“õ “Į—ą–Ī“Ī—Ä—č—ą
–°—Ą–Ķ—Ä–į–Ľ—č“õ “Į—ą–Ī“Ī—Ä—č—ą
“ö–į–∑—Ė—Ä–≥—Ė –∑–į–ľ–į–Ĺ–Ĺ—č“£ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—Ā—č–Ĺ–į —ā–į“ď—č –Ī”©–Ľ—Ė–ľ—ą–Ķ–Ľ–Ķ—Ä “õ–ĺ—Ā—č–Ľ–ī—č:.
–ü–į–Ļ–ī–į–Ľ–į–Ĺ“ď–į–Ĺ ”ô–ī—Ė—Ā—ā–Ķ—Ä—Ė–Ĺ–Ķ –Ī–į–Ļ–Ľ–į–Ĺ—č—Ā—ā—č:
“ö–į—Ä–į–Ņ–į–Ļ—č–ľ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź ‚ÄĒ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –ļ–į—Ä–į–Ņ–į–Ļ—č–ľ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į“ď–į –Ķ–Ĺ–Ķ—ā—Ė–Ĺ –Ī”©–Ľ—Ė–ľ—Ė. “ö–į—Ä–į–Ņ–į–Ļ—č–ľ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –ľ–Ķ–Ĺ –ļ–į—Ä–į–Ņ–į–Ļ—č–ľ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ —ą–Ķ–ļ–į—Ä–į—Ā—č “õ–į—ā–į“£ —ą–Ķ–ļ—ā–Ķ–Ľ–ľ–Ķ–≥–Ķ–Ĺ. “ö–į—Ä–į–Ņ–į–Ļ—č–ľ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ĺ–Ķ–≥—Ė–∑—Ė–Ĺ–Ķ–Ĺ –∂–į–Ľ–Ņ—č –Ī—Ė–Ľ—Ė–ľ –Ī–Ķ—Ä–Ķ—ā—Ė–Ĺ –ľ–Ķ–ļ—ā–Ķ–Ņ—ā—Ė“£ –ĺ“õ—č—ā—É –Ī–į“ď–ī–į—Ä–Ľ–į–ľ–į—Ā—č–Ĺ–į —Ā”ô–Ļ–ļ–Ķ—Ā –ļ–Ķ–Ľ–≥–Ķ–Ĺ—Ė–ľ–Ķ–Ĺ –Ņ”ô–Ĺ–ī—Ė–ļ –į—É“õ—č–ľ—č –ľ“Ī–Ĺ—č–ľ–Ķ–Ĺ —ą–Ķ–ļ—ā–Ķ–Ľ–ľ–Ķ–Ļ–ī—Ė.[3]
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą–ł—Ź–ī–į –∂”ô–Ĺ–Ķ ”©–Ĺ–Ķ—Ä–ī–Ķ
 –ú–į—Ä—ā–ł–Ĺ –ī–Ķ –í–ĺ—Ā. –Ė–Ķ—ā—Ė –į–Ņ–į–Ľ—č-—Ā—Ė“£—Ė–Ľ—Ė–Ľ–Ķ—Ä. 1590
–ú–į—Ä—ā–ł–Ĺ –ī–Ķ –í–ĺ—Ā. –Ė–Ķ—ā—Ė –į–Ņ–į–Ľ—č-—Ā—Ė“£—Ė–Ľ—Ė–Ľ–Ķ—Ä. 1590
–ē–∂–Ķ–Ľ–≥—Ė –ď—Ä–Ķ–ļ–ł—Ź–ī–į–Ĺ-–į“õ “õ–į–Ľ—č–Ņ—ā–į—Ā“õ–į–Ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ –Ĺ–Ķ–≥—Ė–∑—Ė–Ĺ–ī–Ķ —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą–ł—Ź–Ľ—č“õ “Ī“ď—č–ľ–ī–į—Ä –∂–į—ā“õ–į–Ĺ. –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –∂–Ķ—ā—Ė –Ķ—Ä–ļ—Ė–Ĺ ”©–Ĺ–Ķ—Ä–Ľ–Ķ—Ä–ī—Ė“£ –Ī–Ķ—Ā—Ė–Ĺ—ą—Ė—Ā—Ė –Ī–ĺ–Ľ—č–Ņ —Ā–į–Ĺ–į–Ľ–į–ī—č. –ě–Ĺ—č“£ –į–Ľ–ī—č–Ĺ–ī–į –ď—Ä–į–ľ–ľ–į—ā–ł–ļ–į, –†–ł—ā–ĺ—Ä–ł–ļ–į –∂”ô–Ĺ–Ķ –Ē–ł–į–Ľ–Ķ–ļ—ā–ł–ļ–į–ī–į–Ĺ —ā“Ī—Ä–į—ā—č–Ĺ –Ę—Ä–ł–≤–ł—É–ľ –∂”ô–Ĺ–Ķ –ö–≤–į–ī—Ä–ł—É–ľ–Ĺ—č“£ “Į–Ľ–ļ–Ķ–Ĺ “ď—č–Ľ—č–ľ—č - –ź—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ–į –Ī–į—Ä (–ö–≤–į–ī—Ä–ł—É–ľ–ī–į –ź—Ä–ł—Ą–ľ–Ķ—ā–ł–ļ–į –ľ–Ķ–Ĺ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–ī–į–Ĺ –Ī–į—Ā“õ–į - –ú—É–∑—č–ļ–į –∂”ô–Ĺ–Ķ –ź—Ā—ā—Ä–ĺ–Ĺ–ĺ–ľ–ł—Ź –Ī–į—Ä).
¬ę–§–ł–Ľ–ĺ—Ā–ĺ—Ą–ł—Ź –ľ–Ķ–Ĺ –ē—Ä–ļ—Ė–Ĺ–ī—Ė–ļ—ā—Ė“£ “Į–Ļ–Ľ–Ķ–Ĺ—É—Ė¬Ľ —ā—Ä–į–ļ—ā–į—ā—č–Ĺ–ī–į –ú–į—Ä—Ü–ł–į–Ĺ –ö–į–Ņ–Ķ–Ľ–Ľ–į –ĺ—Ā—č –∂–Ķ—ā—Ė ”©–Ĺ–Ķ—Ä–ī—Ė –∂–Ķ—ā—Ė ”ô–Ļ–Ķ–Ľ –ļ–Ķ–Ļ—Ė–Ņ—Ė–Ĺ–ī–Ķ –Ī–Ķ–Ļ–Ĺ–Ķ–Ľ–Ķ–≥–Ķ–Ĺ. “ö–ĺ–Ľ—č–Ĺ–ī–į –≥–Ľ–ĺ–Ī—É—Ā –Ņ–Ķ–Ĺ —Ü–ł—Ä–ļ—É–Ľ—Ć “Ī—Ā—ā–į–Ņ —ā“Ī—Ä“ď–į–Ĺ –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź–Ĺ—č“£ “õ–į—Ā—č–Ĺ–į –≠–≤–ļ–Ľ–ł–ī—ā—č –ļ”©—Ä—Ā–Ķ—ā–ļ–Ķ–Ĺ.
1893 –∂—č–Ľ—č –Ī“Ī–Ľ “ď—č–Ľ—č–ľ–Ĺ—č“£ “õ“Ī—Ä–ľ–Ķ—ā—Ė–Ĺ–Ķ –į—Ā—ā–Ķ—Ä–ĺ–ł–ī—ā—č –į—ā–į“ď–į–Ĺ: –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź.
–Ē–Ķ—Ä–Ķ–ļ–ļ”©–∑–ī–Ķ—Ä
- ‚ÜĎ –Ď–į–Ľ–į–Ľ–į—Ä —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź—Ā—č, III-—ā–ĺ–ľ
- ‚ÜĎ –†–į—Ö–ł–ľ–Ī–Ķ–ļ–ĺ–≤–į –ó.–ú. –ú–į—ā–Ķ—Ä–ł–į–Ľ–ī–į—Ä –ľ–Ķ—Ö–į–Ĺ–ł–ļ–į—Ā—č —ā–Ķ—Ä–ľ–ł–Ĺ–ī–Ķ—Ä—Ė–Ĺ—Ė“£ –į“ď—č–Ľ—ą—č–Ĺ—ą–į-–ĺ—Ä—č—Ā—ą–į-“õ–į–∑–į“õ—ą–į —ā“Į—Ā—Ė–Ĺ–ī—Ė—Ä–ľ–Ķ —Ā”©–∑–ī—Ė–≥—Ė ISBN 9965-769-67-2
- ‚ÜĎ "–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į–Ľ—č“õ –ĺ–Ļ–į—ą–į—Ä", "“ö–į–∑–į“õ —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź—Ā—č" –ź–Ľ–ľ–į—ā—č, 2009 ISBN 9965-893-25-X