Principio di Pontryagin
|
Read other articles:

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) بيت نمير - قرية - تقسيم إداري البلد اليمن المحافظة محافظة أمانة العاصمة (صنعاء) المديرية مدي
Dieser Artikel wurde aufgrund von inhaltlichen Mängeln auf der Qualitätssicherungsseite des Portals Diskriminierung eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Diskriminierung auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die trotz erheblicher Defizite nicht signifikant verbessert werden können. Bitte hilf mit, das Lemma zu verbessern, und beteilige dich bitte an der Diskussion! Der Bundesverband Caritas Behindertenhilfe und Psych...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 10月 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2015年6月) 「十月」はこの項目へ転送されています。雑誌につい...

Hobbes ist eine Weiterleitung auf diesen Artikel. Weitere Bedeutungen sind unter Hobbes (Begriffsklärung) aufgeführt. Thomas Hobbes (Ausschnitt aus einem Gemälde von John Michael Wright, circa 1669–1670) Thomas Hobbes [hɔbz] (geboren am 5. April 1588 in Westport, Wiltshire; gestorben am 4. Dezember 1679 in Hardwick Hall, Derbyshire) war ein englischer Mathematiker, Staatstheoretiker und Philosoph. Er wurde durch sein Hauptwerk Leviathan bekannt, in dem er vor dem Hintergrund des englisc...

Vice President of South Vietnam from 1967 to 1971 In this Vietnamese name, the surname is Nguyễn, but is often simplified to Nguyen in English-language text. In accordance with Vietnamese custom, this person should be referred to by the given name, Kỳ. Nguyễn Cao KỳKỳ in 19662nd Vice President of South VietnamIn office31 October 1967 – 29 October 1971PresidentNguyễn Văn ThiệuPrime Minister Nguyễn Văn Lộc (1967–1968) Trần Văn Hương (1968–1969) Trần...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (يونيو 2023) رئيس الاتحاد السويسري إجنازيو كاسيس البلد سويسرا عن المنصب مقر الإقامة �...

Mobil peliputan di Medan Merdeka, Monumen Nasional, Jakarta. Jakartasentrisme atau Jakartasentris adalah istilah untuk menyebut dominasi budaya, ekonomi dan politik Jakarta terhadap wilayah-wilayah lain di Indonesia. Gagasan Jakartasentrisme mulanya muncul sebagai salah satu permasalahan jurnalisme di Indonesia. Media massa cenderung memberitakan dan menampilkan apa yang terjadi di Jakarta dan karakteristik demografi Jakarta sehingga permasalahan-permasalahan dan masyarakat dari luar kelompok...

Blue Chip Blue chip adalah sebuah istilah dalam pasar modal yang mengacu pada saham dari perusahaan besar yang memiliki pendapatan stabil dan liabilitas dalam jumlah yang tidak terlalu banyak. Istilah ini berasal dari istilah di kasino, di mana blue chips mengacu pada chip yang memiliki nilai paling besar. Saham blue chip biasanya memberikan dividen secara reguler, bahkan ketika bisnis berjalan lebih buruk dari biasanya. Referensi Artikel bertopik keuangan, uang, atau mata uang ini adalah seb...

Overview of television in the Republic of Turkey Part of a series on theCulture of Turkey History Anatolian peoples Genetic history Migration of Turks into Anatolia Constitutional history Diplomatic history Economic history LGBT history Military history Cultural history Jewish history People Abazins Abkhazians Afghans Africans Albanians Arabs Arab Christians Antiochian Greek Christians Bidri Mhallami Armenians Hemşinli Hidden Armenians Assyrians Australians Bosniaks Brazilians Britons Bulgar...
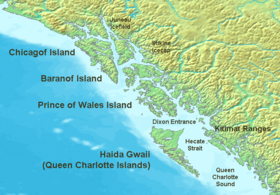
جزيرة ميتكوف معلومات جغرافية المنطقة أرخبيل ألكسندر الإحداثيات 56°35′54″N 132°48′33″W / 56.598333333333°N 132.80916666667°W / 56.598333333333; -132.80916666667 [1] [2] الأرخبيل أرخبيل ألكسندر المسطح المائي المحيط الهادئ المساحة 546 كيلومتر مربع الطول 28 كيلومتر العرض...

Hoax character claimed to be from The Simpsons Fan art of Graggle/Gumbly, which mimics the art style of The Simpsons promotional art. Graggle Simpson or Gumbly is a metafictional character purported to be from the American animated sitcom The Simpsons. He is the subject of an internet meme and hoax in which users online satirically claim that the character was a real member of the series' cast of characters (as well as the Simpson family) that had been removed through retroactive continuity.&...

For the personage from the Ramayana, see Shabari. 2011 Indian filmShabriShabri promotion posterDirected byLalit MaratheWritten byLalit MaratheScreenplay byLalit MaratheStory byLalit MaratheProduced byRam Gopal VarmaStarringIsha KoppikarCinematographyAmit RoyEdited byAvinash WalzadeMusic byRaju SinghDistributed byReliance EntertainmentRelease date 26 August 2011 (2011-08-26) [1]CountryIndiaLanguageHindi Shabri is a 2011 Indian Hindi-language action film directed by Lalit...
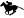
この記事は「旧馬齢表記」が採用されており、国際的な表記法や2001年以降の日本国内の表記とは異なっています。詳しくは馬齢#日本における馬齢表記を参照してください。 ダイワテキサス 第74回中山記念パドック(2000年2月27日)欧字表記 Daiwa Texas[1]品種 サラブレッド[1]性別 牡[1]毛色 栗毛[1]生誕 1993年4月2日[1]死没 2021年11月28日(28歳没)...

Franciscan friary in England – dissolved 1538 Greyfriars LeicesterGreyfriars site superimposed on a modern map of the area. Richard III's burial site is shown by a small dot.Location within LeicestershireMonastery informationOther namesLeicester Franciscan FriaryOrderOrder of Friars MinorEstablishedBefore 1230[1]Disestablished1538[1]Dedicated toUnclear: Possibly Saint Francis of Assisi[2] or Saint Mary Magdalene[3]DioceseLincolnPeopleFounder(s)Unclear Traditi...

The music of the Heroes television series was composed by Wendy Melvoin and Lisa Coleman of the duo, Wendy & Lisa. Some of the scores feature the voice of L. Shankar (credited as Shenkar).[1] The score album and the soundtrack album were released via La-La Land Records. The soundtrack of the series contains some songs, including old ones. Heroes: Original Soundtrack Heroes: Original SoundtrackSoundtrack album by Various artistsReleasedMarch 18, 2008RecordedVarious datesGenrePo...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada.Este aviso fue puesto el 21 de abril de 2019. Las Bibliotecas Municipales de La Coruña están formadas por un servicio central de coordinación y ocho bibliotecas municipales de la ciudad española de La Coruña.Bibliotecas Municipales de La Coruña Estructura Biblioteca Municipal de Estudios Locales (La Coruña)Las Bibliotecas Municipales de La Coruña están constituidas por 8 centros, de los cuales...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2002–03 LEN Champions League – news · newspapers · books · scholar · JSTOR (June 2015) (Learn how and when to remove this template message) Sports season2002–03 LEN Champions LeagueLeagueLEN Champions LeagueSportWater PoloDuration16 October 2002 to17 May 2003Number of teams8...

Italian footballer (born 1987) Andrea Consigli Consigli with Sassuolo in 2014Personal informationDate of birth (1987-01-27) 27 January 1987 (age 36)Place of birth Cormano, ItalyHeight 1.89 m (6 ft 2 in)[1]Position(s) GoalkeeperTeam informationCurrent team SassuoloNumber 47Youth career2004–2006 AtalantaSenior career*Years Team Apps (Gls)2006–2014 Atalanta 193 (0)2006–2007 → Sambenedettese (loan) 32 (0)2007–2008 → Rimini (loan) 35 (0)2014– Sassuolo 331 ...

Island in the Palmer Archipelago, Antarctica Location of Anvers Island in the Antarctic Peninsula region. Gerlache Island is the largest of the Rosenthal Islands lying off Gerlache Point[1] on the west coast of Anvers Island, in the Palmer Archipelago of Antarctica. It was first roughly charted and named Pointe de Gerlache by the French Antarctic Expedition, 1903–05, under Jean-Baptiste Charcot, for Lieutenant Adrien de Gerlache. As a result of surveys by the Falkland Islands Depend...

You can help expand this article with text translated from the corresponding article in Japanese. (2023-10-04) Click [show] for important translation instructions. View a machine-translated version of the Japanese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wiki...


![{\displaystyle H(x^{*}(t),u^{*}(t),\lambda ^{*}(t),t)\leq H(x^{*}(t),u,\lambda ^{*}(t),t),\quad \forall u\in {\mathcal {U}},\quad t\in [t_{0},t_{f}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0467eb8a0973507cff602c16d33efe618bc11120)
![{\displaystyle x^{*}\in C^{1}[t_{0},t_{f}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5e6a1df6192aa4652f258c3b323ebbcfb7d3072)
![{\displaystyle \lambda ^{*}\in BV[t_{0},t_{f}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d2ab7a1e7090f45b74c9f37280f8d2c4b5bd28f)











![{\displaystyle {\dot {x}}=f(x,u),\quad x(0)=x_{0},\quad u(t)\in {\mathcal {U}},\quad t\in [0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ace09d9ccc09a44d71e8dbfb7ba810c9d954ca35)


![{\displaystyle t\in [0,T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7ea7b28971838e52f450c48053939e81daa26f)















