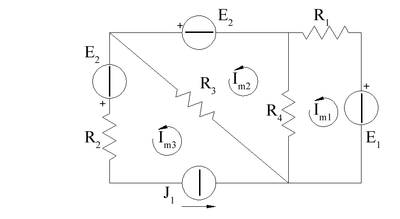
Metodo delle maglie
|
Read other articles:

此生者传记没有列出任何参考或来源。 (2021年8月13日)请协助補充可靠来源,针对在世人物的无法查证的内容将被立即移除。 竹中直人竹中直人在《Ken and Mary》的拍攝現場男演员罗马拼音Naoto Takenaka国籍 日本出生 (1956-03-20) 1956年3月20日(67歲) 日本神奈川縣橫濱市金澤區富岡出道日期1977年活跃年代1977年至今经纪公司From 1st Pro网站官方網站互联网电影数据库(IMDb)信息

Selección de fútbol de las Islas Vírgenes Británicas Datos generalesPaís Islas Vírgenes BritánicasCódigo FIFA VGBFederación Asociación de Fútbol de las Islas Vírgenes BritánicasConfederación CONCACAFSeudónimo(s) The Nature BoyzSeleccionador Chris Kiwomya[1] (desde 2021-)Capitán Troy Caesar[2] Más goles Avondale Williams (5)Más partidos Carlos Septus (24)Clasificación FIFA 207.º (noviembre de 2023)Estadio(s) Campo recreativo A.O. ShirleyEquipaciones Prim...

Field of bodywork emphasizing internal sensation This article is about sensation-based movement practices. For the matter-bound beings in Gnosticism, see hylics. For other uses, see Somatic. Somatic educator Moshe Feldenkrais in 1978, teaching how to rise from a chair Somatics is a field within bodywork and movement studies which emphasizes internal physical perception and experience. The term is used in movement therapy to signify approaches based on the soma, or the body as perceived from w...

Частково визнана держава Турецька Республіка Північного Кіпрутур. Kuzey Kıbrıs Türk Cumhuriyeti Прапор Герб Девіз: national_anthem = İstiklâl Marşı Розташування Турецької Республіки Північного Кіпру Столиця Лефкоша (Нікосія) 35°08′ пн. ш. 33°28′ сх. д.country H G O Найбільше місто Нікосія Виз�...

American think tank National Center for Policy AnalysisAbbreviationNCPAFormation1983Dissolved2017TypePublic policy think tankChief executive officerAllen West (as of 2015)[1]Budget Revenue: $2,629,925Expenses: $3,562,505(FYE September 2015)[2] The National Center for Policy Analysis (NCPA) was a non-profit American think tank[3] whose goals were to develop and promote private alternatives to government regulation and control. Topics it addressed include reforms in heal...

This article is about the Bilal album. For the Active Child album, see Active Child. 2015 studio album by BilalIn Another LifeStudio album by BilalReleasedJune 30, 2015GenreSoulR&Bneo soulhip hop soulfunkpsychedelic soulLength38:28LabeleOneProducerAdrian YoungeBilal chronology A Love Surreal(2013) In Another Life(2015) Voyage-19(2020) In Another Life is the fifth[1] studio album by American singer and songwriter Bilal. It was released on June 30, 2015, by Entertainment One...

Comedy Central UK Fernsehsender (Privatrechtlich) Programmtyp Spartenprogramm (Unterhaltung) Empfang Kabel, Satellit & IPTV Bildauflösung (Eintrag fehlt) Sendestart 6. April 2009 um 21:00 Uhr Sprache Englisch Eigentümer ViacomCBS Website Comedy Central UK & Ireland ist ein Ableger des US-Senders Comedy Central, der bis zum 6. April 2009 noch Paramount Comedy hieß. Weitere Ableger im Vereinigten Königreich und Irland sind Comedy Central Extra, Comedy Central +1 und Comedy Central E...

Ini adalah nama Jepang, nama keluarganya adalah Yoshizawa. Kenkichi Yoshizawa Kenkichi Yoshizawa (芳沢 謙吉code: ja is deprecated , Yoshizawa Kenkichi, 24 Januari 1874 – 5 Januari 1965) adalah seorang diplomat di kekaisaran Jepang, yang menjabat sebagai Menteri Luar Negeri Jepang ke-26 pada 1932. Ia adalah kakek pihak ibu dari Sadako Ogata. Biografi Yoshizawa berasal dari tempat yang sekarang berada di kota Joetsu, prefektur Niigata. Ia adalah lulusan dari departemen sastr...

Chennai Metro's Blue Line metro station Saidapet Chennai Metro stationSaidapet metro station with City Union BankGeneral informationLocationAnna Salai, Todd Hunter Nagar, Nandanam, Chennai, Tamil Nadu 600015IndiaCoordinates13°01′17″N 80°13′32″E / 13.0214141°N 80.2254362°E / 13.0214141; 80.2254362Owned byChennai MetroOperated byChennai Metro Rail Limited (CMRL)Line(s)Blue LinePlatformsIsland platform Platform-1 → Chennai International Airport (to be extend...

Airport in Konya, TurkeyKonya AirportKonya HavalimanıIATA: KYAICAO: LTANSummaryAirport typePublic / militaryOperatorDHMİ (State Airports Administration) Turkish Air ForceLocationKonya, TurkeyElevation AMSL3,381 ft / 1,031 mCoordinates37°58′44.40″N 032°33′42.70″E / 37.9790000°N 32.5618611°E / 37.9790000; 32.5618611Websitekonyahavalimani.comMapKYALocation of airport in TurkeyShow map of TurkeyKYAKYA (Asia)Show map of AsiaRunways Direction Len...

Territory of Canada This article is about the Canadian territory. For other uses, see Yukon (disambiguation). Territory in CanadaYukonTerritory FlagCoat of arms BC AB SK MB ON QC NB PE NS NL YT NT NU Coordinates: 63°N 135°W / 63°N 135°W / 63; -135[1]CountryCanadaBefore confederationDistrict of YukonConfederationJune 13, 1898 (9th)Capital(and largest city)WhitehorseLargest metroWhitehorseGovernment • TypeParliamentary system • Commiss...

American outlaw biker and gangster (1949–1989) Michael O'FarrellO'Farrell in 1984BornMichael Vincent O'Farrell(1949-06-02)June 2, 1949Los Angeles County, California, U.S.DiedJune 6, 1989(1989-06-06) (aged 40)San Leandro, California, U.S.Cause of deathGunshot and stab woundsResting placeEvergreen CemeteryOther namesIrishOccupation(s)Outlaw biker, gangsterKnown forPresident of the Oakland Hells Angels chapterAllegianceNight Riders MC Hells Angels MCConviction(s)Conspiracy ...

Sri Lankan state-owned broadcaster For the British Independent Television network, see ITV (TV network). ITN Ltd redirects here. For the British Independent Television News Limited, see ITN. ITN channel redirects here. For the former British ITN News Channel, see ITV News Channel. This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Independent Television Network – news · new...

French-born Togolese footballer Gilles Sunu Sunu with Lorient in 2013Personal informationFull name Gilles Christ Sunu[1]Date of birth (1991-03-30) 30 March 1991 (age 32)[2]Place of birth Châteauroux, FranceHeight 1.81 m (5 ft 11 in)[2]Position(s) WingerYouth career1997–2007 Châteauroux2007–2009 ArsenalSenior career*Years Team Apps (Gls)2009–2011 Arsenal 0 (0)2009–2010 → Derby County (loan) 9 (1)2010–2011 → Lorient (loan) 9 (0)2011 �...

هيئة البث العامة الأوكرانية(بالأوكرانية: Національна суспільна телерадіокомпанія України) (باختصار NSTU) هي هيئة لخدمة البث العامة، والتي تشمل قناتي تلفزيون وطنيين وقنوات الراديو، و 24 فرعا إقليميا، فضلا عن منصات رقمية.[1] هيئة البث العامة الأوكرانيةالشعارمعلومات عامةا...

2003 studio album by Dianne ReevesA Little MoonlightStudio album by Dianne ReevesReleasedAugust 19, 2003RecordedDecember 4–10, 2002GenreVocal jazzLabelBlue NoteProducerArif MardinDianne Reeves chronology The Calling: Celebrating Sarah Vaughan(2001) A Little Moonlight(2003) Christmas Time Is Here(2004) Professional ratingsReview scoresSourceRatingAllmusic link A Little Moonlight is an album by Dianne Reeves released in 2003. A Little Moonlight won Reeves her third consecutive Grammy ...

State Legislative Assembly Constituency in Tamil Nadu For other places with same/similar name, see Paramathi-Velur (disambiguation). Paramathi-VelurConstituency for the Tamil Nadu Legislative AssemblyConstituency detailsCountryIndiaRegionSouth IndiaStateTamil NaduDistrictNamakkalLS constituencyNamakkalTotal electors2,21,602[1]Member of Legislative Assembly16th Tamil Nadu Legislative AssemblyIncumbent Sekar S Party AIADMKElected year2021 Paramathi-Velur is a state assembly c...

Not to be confused with Realms (video game). 1996 video gameRealmNorth American box artDeveloper(s)Titus FrancePublisher(s)Titus FranceFlair Software Ltd.Platform(s)Super NESReleaseNA: December 1996EU: February 27, 1997Genre(s)2D action platformerMode(s)Single-player Realm is a platform video game with shooting elements that was released exclusively for the Super Nintendo Entertainment System in 1996. Story Firing red energy shots at a bunch of enemies that resemble fireballs. Realms takes pl...

Period of Polish history King of Poland and Grand Duke of Lithuania – Sigismund II Augustus and Queen of Poland, Grand Duchess consort of Lithuania – Barbara Radziwiłł in Vilnius by Jan Matejko. The Polish Golden Age (Polish: Złoty Wiek Polski) was the Renaissance period in Poland and the Grand Duchy of Lithuania, roughly corresponding to the period of rule of the King Sigismund I the Old (1506–1548) and his son, Sigismund II Augustus, the last of the Jagiellonian Dynasty monarchs, u...

Aubrey Plaza nel 2019 Aubrey Christina Plaza (Wilmington, 26 giugno 1984) è un'attrice, comica e cabarettista statunitense. È nota per aver recitato nella serie comica Parks and Recreation dal 2009 al 2015, e nella serie drammatica Legion dal 2017 al 2019. Nel 2022 ha recitato nella serie The White Lotus, per la quale si è aggiudicata uno Screen Actors Guild Award. Nel 2023 la rivista Time l'ha nominata una delle 100 persone più influenti al mondo.[1] Indice 1 Biografia 2 Filmogra...