צבר מיקרוקנוני
| |||||||||||||||||||
Read other articles:

ميكرون موناستيريون الإحداثيات 40°42′18″N 22°32′30″E / 40.705°N 22.5417°E / 40.705; 22.5417 تقسيم إداري البلد اليونان[1] خصائص جغرافية ارتفاع 11 متر عدد السكان عدد السكان 1306 (2011) معلومات أخرى منطقة زمنية ت ع م+02:00 (توقيت قياسي)، وت ع م+03:00 (توقيت صيفي) 570 ...

Vrije Universiteit AmsterdamVrije Universiteit Amsterdam[1] Latijnse naam Universitas Libera (Reformata Amstelodamensis) Motto Auxilium nostrum in nomine Domini Locatie Amsterdam, Nederland Opgericht 1880 Type bijzonder onderwijs Rector Prof. dr. Jeroen Geurts[2] Studenten 24.517 (2012)[3] Personeel 4669 (2012)[3] Lid van EUA, SAE, Santander, Aurora Website Portaal Onderwijs De Vrije Universiteit Amsterdam (afgekort VU) is een brede onderzoeks- en ...

Stasiun Kassemba合戦場駅Pintu keluar timur Stasiun Kassemba pada Agustus 2021Lokasi513 Kassemba Tsuga-machi, Tochigi, Tochigi(栃木県栃木市都賀町合戦場513)JepangKoordinat36°24′28″N 139°44′28″E / 36.4079°N 139.7412°E / 36.4079; 139.7412Koordinat: 36°24′28″N 139°44′28″E / 36.4079°N 139.7412°E / 36.4079; 139.7412Pengelola Tobu RailwayJalur Jalur Tobu NikkoLetak dari pangkal50.0 km dari Tōbu-Dōbutsu-Kōen...

Кримська татарка. Картина французького художника, 1920 рік Етикет кримських татар — норми і правила поведінки, принципи моралі і моральності кримських татар. Протягом століть у кримських татар, одночасно з їх етногенезом у Криму, під впливом Ісламу формувалася особлива с�...

هيجة عبادي على (محلة) تقسيم إداري البلد اليمن المحافظة محافظة إب المديرية مديرية العدين العزلة عزلة قصل القرية قرية الزائدة السكان التعداد السكاني 2004 السكان 20 • الذكور 11 • الإناث 9 • عدد الأسر 5 • عدد المساكن 5 معلومات أخرى التوقيت توقيت اليمن (+3 غرينيتش) �...

Bupati TambrauwLambang Kabupaten TambrauwPetahanaEngelbertus Gabriel Kocusejak 22 Mei 2023Masa jabatan5 tahunDibentuk15 April 2009Pejabat pertamaGabriel AsemSitus webtambrauwkab.go.id Berikut ini adalah Daftar Bupati Tambrauw dari masa ke masa. No. Bupati Awal Menjabat Akhir Menjabat Periode Wakil Bupati Ket. — Drs.Menase Paa,M.Si. 15 April 2009 29 Oktober 2011 — — [Ket. 1] 1 Gabriel AsemS.E., M.Si. 29 Oktober 2011 29 Oktober 2016 1 Yohanes Yembra [2] — tidak dike...

Branchwork on the baptismal font of Worms Cathedral Branchwork tracery at Ulm Minster, c. 1475 Branchwork portal of the former monastery church of Chemnitz (1525) Branchwork or branch tracery (German: Astwerk, Dutch: Lofwerk of Loofwerk) is a type of architectural ornament often used in late Gothic architecture and the Northern Renaissance, consisting of knobbly, intertwined and leafless branches. Branchwork was particularly widespread in Central European art between 1480 and 1520 and can be ...

RANBP3 التراكيب المتوفرة بنك بيانات البروتينOrtholog search: PDBe RCSB قائمة رموز معرفات بنك بيانات البروتين 2CRF, 2Y8F, 2Y8G المعرفات الأسماء المستعارة RANBP3, RAN binding protein 3 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 603327 MGI: MGI:1919060 HomoloGene: 136516 GeneCards: 8498 علم الوجود الجيني الوظيفة الجزيئية • ...

Wiess School of Natural SciencesMottoThe Frontiers of KnowledgeTypePrivateEstablished1912DeanThomas C. KillianLocationHouston, Texas, United States29°43′09″N 95°24′05″W / 29.7191°N 95.4013°W / 29.7191; -95.4013AffiliationsRice UniversityWebsite[1] [2] The Wiess School of Natural Sciences is an academic school at Rice University in Houston, Texas. It comprises the departments of BioSciences (a merging of Biochemistry and Cell Biology and Ecology and Evolutio...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2023) غزوان الزركلي معلومات شخصية تاريخ الميلاد 4 يناير 1954 (العمر 69 سنة) الحياة العملية المهنة عازف بيانو تع�...

Gaya atau nada penulisan artikel ini tidak mengikuti gaya dan nada penulisan ensiklopedis yang diberlakukan di Wikipedia. Bantulah memperbaikinya berdasarkan panduan penulisan artikel. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapat memahami maksud dari Bupati Kraksaan. Contoh paragraf pembuka Bupati Kraksaan adalah .... (Pelaj...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2021) خط سكة حديد بوتين-فيينتيان البلد لاوس تاريخ الافتتاح الرسمي 3 ديسمبر 2021[1] طول الخط 414 كيلومتر مقياس السكة سكة حديد قياس 1435 ملم تعديل مصد�...

Municipality in Kyustendil, BulgariaNevestino Municipality Община НевестиноMunicipalityNevestinoCoordinates: 42°15′N 22°51′E / 42.250°N 22.850°E / 42.250; 22.850CountryBulgariaProvinceKyustendilMunicipalityNevestinoArea • Total439.69 km2 (169.77 sq mi)Population (1-Feb-2011) • Total2,821 • Density6.4/km2 (17/sq mi)Time zoneUTC+2 (EET) • Summer (DST)UTC+3 (EEST)Websitewww.obs...

Antoninian des Numerian Numerian (* 253; † 284), mit vollständigem Namen Marcus Aurelius Numerius Numerianus, war ein römischer Kaiser. Er regierte von 283 bis 284 zusammen mit seinem älteren Bruder Carinus das Römische Reich, wobei ihm die Verwaltung der Ostprovinzen oblag. Leben Numerian wurde als jüngster Sohn des späteren Kaisers Carus 253 an einem unbekannten Ort geboren. Nachdem sein Vater den Thron bestiegen hatte, erhob er zunächst Carinus, bald darauf auch Numerian in den Ra...

Dutch pole vaulter Christian Tamminga in 2008. Christian Tamminga (born 30 April 1974 in Leiden) is a retired Dutch athlete who specialised in the pole vault.[1] His biggest success was the sixth place at the 2001 World Championships. His personal bests in the event are 5.76 metres outdoors (1998) and 5.60 metres indoors (2002).[citation needed] After retiring, he started a company manufacturing athletics equipment.[2] Competition record Year Competition Venue Position...

Johann Heinrich von Thünen (Canarienhausen (bij Waddewarden), 24 juni 1783 - Tellow (in Warnkenhagen), 22 september 1850) was een Duits econoom. Leven en werk Von Thünen studeerde landbouwwetenschap en wiskunde in Celle en Göttingen. Daarna vestigde hij zich op het landgoed Tellow in Warnkenhagen in de buurt van Rostock. Baanbrekend was zijn wiskundige benadering van economische kwesties, gecombineerd met empirische toetsing van zijn modellen. Hij bood systematische verklaringen voor de ho...

Head of the Catholic Church from 1878 to 1903 PopeLeo XIIIBishop of RomeOfficial photograph, 1898[a]ChurchCatholic ChurchPapacy began20 February 1878Papacy ended20 July 1903PredecessorPius IXSuccessorPius XOrdersOrdination31 December 1837by Carlo OdescalchiConsecration19 February 1843by Luigi LambruschiniCreated cardinal19 December 1853by Pius IXPersonal detailsBornGioacchino Vincenzo Raffaele Luigi Pecci2 March 1810Carpineto Romano, département of Rome, French EmpireDied20...

Species of bird African harrier-hawk Adult, settled on sand bank and in flight Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Accipitriformes Family: Accipitridae Genus: Polyboroides Species: P. typus Binomial name Polyboroides typusSmith, 1829 Subspecies[2] P. t. typus - Smith, A, 1829 P. t. pectoralis - Sharpe, 1903 The African harrier-hawk, harrier hawk or gymnogene ...

Lighthouse in New Zealand LighthouseKātiki Point LighthouseMoeraki LocationKātiki Point, South Island New ZealandCoordinates45°23′30.7″S 170°51′58.2″E / 45.391861°S 170.866167°E / -45.391861; 170.866167TowerConstructed1878Constructionwooden towerAutomated1975Height8 metres (26 ft)Shapehexagonal tower with balcony and lanternMarkingswhite tower, red trim, black lanternPower sourcemains electricity OperatorMaritime New ZealandLightFirst lit187...
Part of a series onPizza Main articles History of pizza Pizza delivery List of pizza varieties by country Pizza varieties Al taglio Altoona-style Beach California-style Capricciosa Chicago-style Chocolate Colorado-style Dayton-style Detroit-style Focaccia al rosmarino Fugazza Grandma Greek Happy Hawaiian Iranian Kebab Lazio Margherita Marinara Matzah Meatball Mexican Neapolitan New Haven–style New York–style Ohio Valley-style Pan Pictou County Pizzetta Pugliese Quad City–style Quattro f...















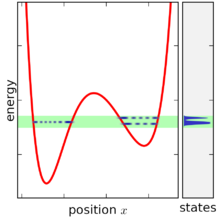












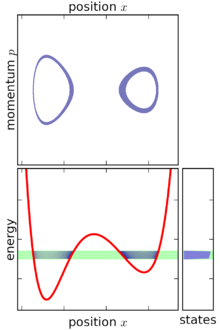













![{\displaystyle h=1_{[energy\ unit]\times [time\ unit]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc47ca73d9f2919c7df276d4630ec5f4755c9bd)


