Théorie de la calculabilité
|
Read other articles:

Australian rules footballer and cricketer This article is about the Australian rules football player. For other people, see Charles Baker (disambiguation). Australian rules footballer Charlie Baker Personal informationFull name Charles Michael BakerDate of birth (1880-06-18)18 June 1880Place of birth Ballarat East, VictoriaDate of death 4 May 1962(1962-05-04) (aged 81)Place of death Ballarat, VictoriaOriginal team(s) St Pats, BallaratHeight 175 cm (5 ft 9 in)Playing c...

Logo des OF Das Občanské fórum (OF; deutsch: Bürgerforum) war eine politische Bewegung im tschechischen Landesteil der damaligen Tschechoslowakei in der Zeit der Samtenen Revolution. Es entstand am 19. November 1989, zwei Tage nach Beginn der Revolution, in Prag als eine spontane Plattform für diverse bürgerliche Aktivitäten. Das OF lehnte das totalitäre kommunistische Regime ab. Es war ab Dezember 1989 an der „Regierung der nationalen Verständigung“ beteiligt und wurde bei ...
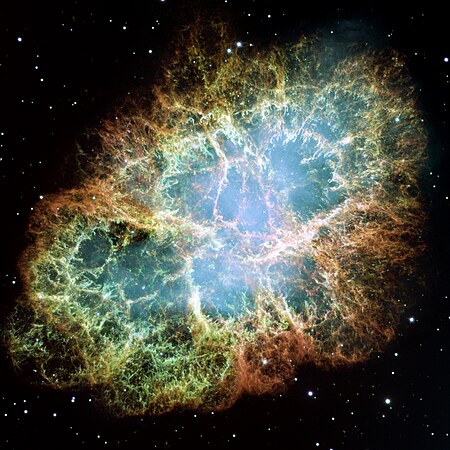
4625 ЩедрінВідкриттяВідкривач Карачкіна Людмила ГеоргіївнаМісце відкриття КрАОДата відкриття 20 жовтня 1982ПозначенняНазвана на честь Щедрін Родіон КостянтиновичТимчасові позначення 1982 UG6 1975 BO 1982 XR4 1986 RC17Категорія малої планети Астероїд головного поясуОрбітальні характ�...
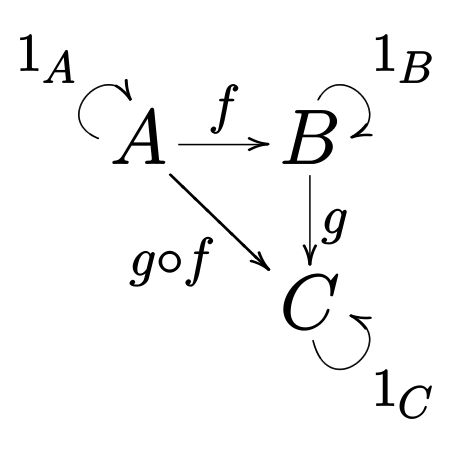
Untuk kegunaan lain, lihat Kategori (disambiguasi) § Matematika. Artikel ini bukan mengenai Kategori:Matematika. Kategori dengan kumpulan objek A, B, C dan kumpulan morfisme yang dilambangkan dengan f, g, g ∘ f, dan loop adalah panah identitas. Kategori ini biasanya dilambangkan dengan huruf tebal 3. Dalam matematika, kategori (terkadang disebut kategori abstrak untuk membedakannya dari kategori konkret) adalah kumpulan objek yang dihubungkan oleh panah. Kategori memiliki dua properti...

This is a list of Japanese snacks (お菓子, okashi) and finger foods. It includes both brand name and generic snacks. Types Anko, or sweet bean paste Anko is a kind of sweet bean paste.[1] Anko is mainly eaten during the afternoon green tea time in Japan. School students eat it after school, at home. Botamochi Daifuku Ichigodaifuku [ja] - Daifuku with strawberry Dorayaki Manjū Monaka Imagawayaki Kusa mochi Taiyaki Yōkan Botamochi Daifuku Ichigo daifuku Dorayaki Imag...

1923 film Other Men's DaughtersLobby cardDirected byBen F. WilsonWritten byEvelyn CampbellFrank SullivanProduced byBen F. WilsonStarringBryant WashburnKathleen KirkhamWheeler OakmanCinematographyEdward LindenJack StevensProductioncompanyBryant Washburn ProductionsDistributed byGrand Asher Distributing CorporationRelease date October 1923 (1923-10) Running time60 minutesCountryUnited StatesLanguageSilent (English intertitles) Other Men's Daughters is a 1923 American silent drama film...

Indian political party Indian political party Telugu Desam Party AbbreviationTDPPresidentN. Chandrababu NaiduGeneral SecretaryNara LokeshParliamentary ChairpersonGalla JayadevLok Sabha LeaderRam Mohan Naidu KinjarapuRajya Sabha LeaderKanakamedala Ravindra KumarFounderN. T. Rama RaoFounded29 March 1982; 41 years ago (1982-03-29)HeadquartersNTR Bhavan, Mangalagiri, Amaravati, Andhra Pradesh, IndiaStudent wingTelugu Nadu Students Federation[1]Youth w...

Uhelná Uhelná (Hrádek nad Nisou) (Tschechien) Basisdaten Staat: Tschechien Tschechien Region: Liberecký kraj Bezirk: Liberec Gemeinde: Hrádek nad Nisou Geographische Lage: 50° 52′ N, 14° 54′ O50.86583333333314.898888888889336Koordinaten: 50° 51′ 57″ N, 14° 53′ 56″ O Höhe: 336 m n.m. Einwohner: 33 (1. März 2001) Postleitzahl: 463 34 Kfz-Kennzeichen: L Verkehr Straße: Václavice – Uhelná historische Lith...

Evil character or person Several terms redirect here. For other uses, see Villain (disambiguation), Villainy (disambiguation), Bad Guy (disambiguation), and Badman (disambiguation). Not to be confused with the feudal term Villein. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article b...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر مغاير للذي أنشأها؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (يناير 2021) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فض�...

Milanese noble family Not to be confused with Visconti of Pisa and Sardinia. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Visconti of Milan – news · newspapers · books · scholar · JSTOR (September 2010) (Learn how and when to remove this template message) ViscontiVicecomesCoat of arms of the Visconti of M...

Research carried out for the children's TV shows In 1969, the children's television show Sesame Street premiered on the National Educational Television network (later succeeded by PBS) in the United States. Unlike earlier children's programming, the show's producers used research and over 1,000 studies and experiments to create the show and test its impact on its young viewers' learning. By the end of the program's first season, Children's Television Workshop (CTW), the organization founded t...

This article is about the district. For its eponymous headquarters, see Shahdol. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Shahdol district – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) District of Madhya Pradesh in IndiaShahdol distr...

Hip-hop duo This article is about the hip hop duo. For their eponymous debut album, see Run the Jewels (album). For the JPEGMafia and Danny Brown song, see Scaring the Hoes. Run the JewelsKiller Mike (left) and El-P in 2014Background informationAlso known asRTJYankee and the BraveOriginUnited StatesGenres Hip hop political hip hop Years active2013–presentLabels Jewel Runners RBC/BMG Mass Appeal Fool's Gold Big Dada Definitive Jux Seeker Music Members El-P Killer Mike Websiterunthejewels.com...

КоммунаЛузиньякLouzignac 45°50′00″ с. ш. 0°14′00″ з. д.HGЯO Страна Франция Регион Пуату — Шаранта Департамент Шаранта Приморская Кантон Мата История и география Площадь 6,13 км²[1] Часовой пояс UTC+1:00, летом UTC+2:00 Население Население 161 человек (2010) Цифровые иден�...

1919 American filmThe Stronger VowAd featuring Geraldine FarrarDirected byReginald BarkerWritten byIzola ForresterProduced bySamuel GoldwynStarringGeraldine FarrarCinematographyPercy Hilburn (French)Distributed byGoldwyn PicturesRelease dateApril 27, 1919Running time6 reelsCountryUnited StatesLanguageSilent (English intertitles) The Stronger Vow is a 1919 American silent melodrama film directed by Reginald Barker and distributed by Samuel Goldwyn.[1][2] It is not known whether...

Tiziano Ferro discographyFerro performing in 2006Studio albums8Compilation albums1Video albums1Music videos28Singles29Box sets1 The discography of Italian pop singer-songwriter Tiziano Ferro consists of eight studio albums, a greatest hits album, one video album, thirty-one singles as lead singer, twelve singles as a featured artist and a box set. Albums Studio albums List of albums, with selected chart positions, sales, and certifications Title Album details Peak chart positions Sales Certif...

BC AB SK MB ON QC NB PE NS NL YT NT NU List of premiers by province Canada is a federation that comprises ten provinces and three territories. Its government is structured as a parliamentary democracy, with a Prime Minister as its head of government; and a constitutional monarchy, with King Charles III as its sovereign. Each of the country's provinces and territories has a head of government, called premier in English and premier ministre—the same term used for the federal leader�...

Lingua guarani Lingua extincte Nomine native: Avañe'ẽ instantia de: lingua[*], macrolanguage[*], lingua moderne[*] subclasse de: Tupi–Guarani[*] Create per: {{{creator}}} in {{{data}}} Contexto: {{{contexto}}} Parlate in: {{{statos}}} Regiones:Parlate in: {{{region}}} Periodo: {{{periodo}}} Personas: Scriptura: alphabeto latin Typologia: {{{typologia}}} Phylogenese: ...

Advanced Technology CollegeEstablished2001LocationDaytona Beach, Florida, USAWebsitehttp://www.daytonastate.edu/catalog/facts/atc.html The Advanced Technology College (ATC) is a four-year technical college located in Daytona Beach, Florida in the United States. This technical college carries courses such as computer technology, construction, manufacturing, engineering, and automotive services. The ATC is involved in a joint-partnership program with Volusia County and Flagler County school dis...




