Preuve ontologique de Gödel
|
Read other articles:

Rikuzen-Takata陸前高田Stasiun Rikuzen-Takata pada Desember 2018LokasiTakata-cho Naruishi 42-5, Rikuzentakata-shi, Iwate-ken 029-2205JepangKoordinat39°00′46″N 141°37′33″E / 39.012737°N 141.625889°E / 39.012737; 141.625889Pengelola JR EastJalur■ Jalur ŌfunatoLetak dari pangkal85.4 km dari IchinosekiJumlah peron2 peron sampingKonstruksiJenis strukturAtas tanahInformasi lainStatusMemiliki stafSitus webSitus web resmiSejarahDibuka15 Desember 1933Ditutup11...

Märchenerzählungen (Cuentos de hadas) en si bemol mayor, Op. 132 es un pieza camerística para trío de clarinete (violín ad libitum), viola y piano compuesta por Robert Schumann entre el 9 y el 11 de octubre de 1853 y publicada en 1854 por Breitkopf & Härtel. La obra está dedicada a su alumno Albert Dietrich.[1][2] Historia Clara Schumann, pianista de la primera interpretación, fotografiada en 1853, el año de la composición. La composición de esta pieza se llevó a...

Лєна Ендре Дата народження 8 липня 1955(1955-07-08)[1][2][3] (68 років)Місце народження Lidingö församlingd, Лідінґе, лен Стокгольм, Швеція[3]Громадянство ШвеціяAlma mater Swedish National Academy of Mime and Actingd[4]Професія акторкаНагороди премія Юджина О'Нілаd Amanda Award for Best Actressd (2003) A...

No debe confundirse con Ogiges. Ogigia Odisea Hermes dice a Calipso que ha de dejar partir a Odiseo.InformaciónTipo Isla míticaNombre original Ὠγυγία[editar datos en Wikidata] Ogigia (en griego antiguo: Ὠγυγίη, Ὠγυγία) es una isla mencionada en la Odisea de Homero, donde habitaba la ninfa Calipso, quien retuvo al héroe griego Odiseo a su regreso de la Guerra de Troya. Etimología Ὠγυγίη parece la forma femenina de un adjetivo ὀγύγιος, de sentid...

محرك أوتو محرك أوتو أو محرك بنزين هو مصطلح يستعمل للدلالة على محرك الاحتراق الداخلي الذي يتم فيه إشعال خليط الوقود والهواء بواسطة شرارة.[1][2][3] يختلف هذا المحرك عن محرك الديزل الذي تتم عملية الإشعال فيه نتيجة للضغط. قد يكون المحرك ذو مشواران (شوطان) أو ذو أربعة مشا

Portion of the US Constitution regarding the executive branch This article is part of a series on theConstitutionof the United States Preamble and Articles Preamble I II III IV V VI VII Amendments to the Constitution I II III IV V VI VII VIII IX X XI XII XIII XIV XV XVI XVII XVIII XIX XX XXI XXII XXIII XXIV XXV XXVI XXVII Unratified Amendments: Congressional Apportionment Titles of Nobility Corwin Child Labor Equal Rights D.C. Voting Rights History Drafting and ratification timeline Conventio...

Норвезьке товариство охорони природи Оригінальна назва бук. Norges NaturvernforbundДата заснування 1914Тип Громадська організаціяГолова Truls GulowsendКількість членів 35 000[1]Адреса ОслоДжерела фінансування членські внески, пожертви, грантиОфіційний сайт www.naturvernforbundet.no Норвезьке �...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (novembre 2022). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références » En pratique : Quelles sources sont attendues ? C...

Sporting event delegationChinese Taipei at the1988 Summer OlympicsChinese Taipei Olympic flagIOC codeTPENOCChinese Taipei Olympic CommitteeWebsitewww.tpenoc.net (in Chinese and English)in SeoulCompetitors61 (43 men, 18 women) in 13 sportsFlag bearer Lee Fu-anMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)195619601964196819721976–198019841988199219962000200420082012201620202024Other related appearances Republic of China (1924–1948) The Republic...

The door of the vault of Milntown Castle, in the grounds of the later Tarbat House, as described by Alexander Mackenzie in 1898: The only remains of the old castle still extant are the door of the vault and the high terraces Milntown Castle was an early 16th-century castle which was situated near Milton, in Easter Ross, in the Scottish Highlands. History The castle was built by the Munro of Milntown family, a cadet branch of the Clan Munro. In 1656, the castle and estate was sold to George Ma...

Перше зображення надмасивної чорної діри M87, зроблене за допомогою телескопа горизонту подій, опубліковане в квітні 2019 року. Інформаційний парадокс чорної діри Стівена Гокінга — це фізична проблема, що виникає з теоретичного розгляду взаємодії квантової механіки та ...

1940 film Texas Rangers Ride AgainTheatrical release posterDirected byJames P. HoganScreenplay byWilliam R. LipmanHorace McCoyProduced byWilliam LeBaronStarringEllen DrewJohn HowardAkim TamiroffMay RobsonBroderick CrawfordCharley GrapewinJohn MiljanCinematographyArchie StoutEdited byArthur P. SchmidtMusic byJohn LeipoldProductioncompanyParamount PicturesDistributed byParamount PicturesRelease date December 13, 1940 (1940-12-13) Running time68 minutesCountryUnited StatesLanguage...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (February 2018) (Learn how and when to remove this template message) 2005 Japanese filmReincarnationTheatrical release posterDirected byTakashi ShimizuScreenplay by Takashi Shimizu Masaki Adachi[1] Produced byTakashige Ichise[1]Starring Yūka Karina Kippei Shiina Tetta Sugimoto[1] Cinemato...

2023 Korean film directed by Lee Won-suk Killing RomanceDirected byLee Won-sukWritten byPark Jeong-yeStarring Lee Hanee (Honey Lee) Lee Sun-kyun Gong Myoung ProductioncompanyWarner BrothersRelease date April 14, 2023 (2023-04-14) (South Korea) Running time106 minutesCountrySouth KoreaLanguageKorean Killing Romance (Korean: 킬링 로맨스) is a 2023 South Korean musical romance comedy film by director Lee Won-suk, starring Lee Hanee (Honey Lee), Lee Sun-kyun, and Gong Myou...

Indian Army regiment 6 LancersActive1984 – presentCountry IndiaAllegianceIndiaBranch Indian ArmyTypeArmourSizeRegimentMotto(s)Dridhta Shaurya Sada Buland (Determination and Valour, always to the fore)ColorsMaroon, French Grey and Forest Green.EquipmentT-90[1]CommandersColonel ofthe RegimentLieutenant General Vivek Kashyap[2]InsigniaAbbreviation6LMilitary unit The 6th Lancers is an armoured regiment of the Indian Army. Formation 6 Lancers was raised on 1 Februa...

Whyalla Football League Inc.Current season, competition or edition: 2021SportAustralian rules footballFounded1920; 103 years ago (1920)No. of teams7Country AustraliaConfederationSANFLMost recentchampion(s)Central Whyalla (2021)Most titlesCentral Whyalla (28)Official websitewhyallafootball.com.au The Whyalla Football League Inc. is an Australian rules football competition based in the town of Whyalla on the east coast of the Eyre Peninsula region of South Australia. It i...

Doug DuceyGubernur Arizona ke-23PetahanaMulai menjabat 5 Januari 2015PendahuluJan BrewerBendahara Arizona ke-42Masa jabatan3 Januari 2011 – 5 Januari 2015GubernurJan BrewerPendahuluDean MartinPenggantiJeff DeWit Informasi pribadiLahirDouglas Anthony Roscoe Jr.9 April 1964 (umur 59)Toledo, Ohio, ASPartai politikRepublikSuami/istriAngela Ducey (m. 1992)Anak3PendidikanArizona State University, Tempe (BS)Situs webSitus web pemerintahanSunting kot...

Sporting event delegationHungary at theOlympicsIOC codeHUNNOCHungarian Olympic CommitteeWebsitewww.olimpia.hu (in Hungarian and English)Medals Gold 183 Silver 156 Bronze 182 Total 521 Summer appearances189619001904190819121920192419281932193619481952195619601964196819721976198019841988199219962000200420082012201620202024Winter appearances192419281932193619481952195619601964196819721976198019841988199219941998200220062010201420182022Other related appearances1906 Intercalated Games This is...

Welsh judge and Member of Parliament SirWilliam JonesSir William Jones in a 1675 engraving by William SherwinMember of the 1597, 1604 and 1614 Parliamentfor BeaumarisMember of the 1601 Parliamentfor Caernarvonshire Personal detailsBorn1566Died(1640-12-09)9 December 1640 Sir William Jones (1566–1640) was a Welsh judge, and a Member of Parliament (MP) for the Welsh Borough of Beaumaris.[1] Life From a family settled in North Wales, he was eldest son of William Jones of Castellmarch, C...
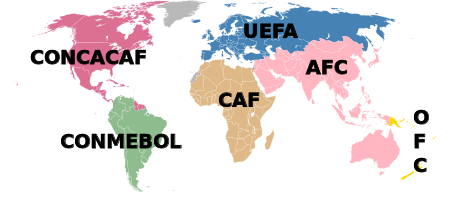
Eliminatórias da Copa do Mundo FIFA de 2010 Dados Período 25 de agosto de 2007 – 18 de novembro de 2009 ◄◄ 2006 2014 ►► As eliminatórias da Copa do Mundo FIFA de 2010 consistiram em uma série de torneios organizados pelas seis confederações afiliadas à FIFA para definir 31 vagas de acordo com critérios estabelecidos por cada região para a máxima competição de futebol. As disputas iniciaram-se no dia 25 de agosto de 2007, e encerraram-se em 18 de novembro de 2009. A distr...
![{\displaystyle {\begin{array}{rl}{\mbox{Ax. 1.}}&P(\varphi )\land \Box \;\forall x[\varphi (x)\rightarrow \psi (x)]\rightarrow P(\psi )\\{\mbox{Ax. 2.}}&P(\neg \varphi )\iff \neg P(\varphi )\\{\mbox{Th. 1.}}&P(\varphi )\rightarrow \Diamond \;\exists x\;[\varphi (x)]\\{\mbox{Df. 1.}}&G(x)\iff \forall \varphi [P(\varphi )\rightarrow \varphi (x)]\\{\mbox{Ax. 3.}}&P(G)\\{\mbox{Th. 2.}}&\Diamond \;\exists x\;G(x)\\{\mbox{Df. 2.}}&\varphi \;\operatorname {ess} \;x\iff \varphi (x)\land \forall \psi \lbrace \psi (x)\rightarrow \Box \;\forall y[\varphi (y)\rightarrow \psi (y)]\rbrace \\{\mbox{Ax. 4.}}&P(\varphi )\rightarrow \Box \;P(\varphi )\\{\mbox{Th. 3.}}&G(x)\rightarrow G\;\operatorname {ess} \;x\\{\mbox{Df. 3.}}&E(x)\iff \forall \varphi [\varphi \;\operatorname {ess} \;x\rightarrow \Box \;\exists y\;\varphi (y)]\\{\mbox{Ax. 5.}}&P(E)\\{\mbox{Th. 4.}}&\Box \;\exists x\;G(x)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83f6445e29b47f2207249afc67826826ff8c2930)







