Geometría proyectiva
|
Read other articles:

У Вікіпедії є статті про інші значення цього терміна: полк імені Богдана Хмельницького (значення). Окрема президентська бригада(з 2022) Окремий президентський полк(1999—2022) Нарукавний знак бригади, 2016 р.Засновано 2 січня 1992 рокуКраїна УкраїнаВид Сухопутні військаТип піхот

Pitres Sombowadile (lahir 28 Mei 1966) adalah seorang penyair, penulis, aktivis, jurnalis dan budayawan Indonesia kelahiran Manado. Ia merupakan lulusan sarjana teknik kelautan ITM Tomohon. Sejak 1991, ia aktif dalam banyak kegiatan kebudayaan. Ia menaungi Majalah Kristen Narwastu (Jakarta 1993); Majalah Pengembangan SDM Sukma (Jakarta 1994); Tabloid Kabar (Manado, 1999-2003); Media Perbatasan Sasahara (2015-2016) dan lain sebagainya.[1] Ia membuat beberapa buku baik sendiri maupun be...

Anton I. von Aldenburg Anton I. von Aldenburg, (* 1. Februar 1633 in Kirchhatten; † 27. Oktober 1680 in Varel) war ein deutscher Reichsgraf und als illegitimer Sohn von Anton Günther von Oldenburg (1583–1667) nach dessen Tod Statthalter der Grafschaften Oldenburg und Delmenhorst für den dänischen König. Inhaltsverzeichnis 1 Leben 1.1 Eltern 1.2 Frühe Jahre 1.3 Statthalter von Oldenburg und Delmenhorst 2 Familie 3 Auszeichnungen 4 Literatur 5 Weblinks 6 Einzelnachweise Leben Elte...

Jacopo Amigoni: Marquis de Ensenada, 1750Zenón de Somodevilla y Bengoechea, Marqués de la Ensenada (* 2. Juni 1702 in Alesanco bei Logroño, Spanien; † 2. Dezember 1781 in Medina del Campo) war ein spanischer Staatsmann, der unter drei Königen von Spanien – Philipp V. (1700–1746), Ferdinand VI. (1713–1756) und Karl III. (1756–88) – eine durchgreifende, erfolgreiche Reformpolitik im Sinn des aufgeklärten Absolutismus verfolgte, die auf innenpolitische Festigung und militärisch...

Supermercados Teloloapan logo Supermercado Teloloapan #7 in Gulfton, Houston Supermercados Teloloapan (Teloloapan Supermarkets) is a chain of supermarkets located in Texas, with its headquarters in Houston,[1] and with locations in Greater Houston and Dallas-Fort Worth. As of 2008 there are nine supermarkets, with most of them being located in Hispanic neighborhoods.[2] Patricia Pedraza, in the Hablando entre Lenguas (Speaking between languages) column of Hoy Tamaulipas (Tamau...

Lihat I, i di Wiktionary, kamus gratis. Alfabet Latindasar ISO AaBbCcDdEeFfGgHhIiJjKkLlMmNnOoPpQqRrSsTtUuVvWwXxYyZz lbs Halaman ini memuat artikel tentang huruf I dalam alfabet Latin. Untuk penggunaan lainnya, lihat I (disambiguasi). Huruf I atau j adalah huruf ke-9 dalam alfabet Latin. I merupakan lambang angka 1 (satu) atau tahun 1 dalam angka Romawi. Sejarah Hieroglif Mesirlengan →Proto-Semitikyad →Fenisiayodh →Yunani Kunoiota →EtruriaI →Latin ModernI Dal...

The Spy First edition (US)AuthorClive Cussler & Justin ScottCountryUnited StatesLanguageEnglishSeriesIsaac Bell talesGenreThriller novelPublisherG. P. Putnam's Sons (US)Michael Joseph (UK)Publication dateJune 1, 2010Media typePrint (hardcover)Pages448 pp (first edition, hardcover)ISBN0-399-15643-7 (first edition, hardcover)Preceded byThe Wrecker (2009) Followed byThe Race (2011) The Spy is an Isaac Bell adventure tale, the third in that series. The hardcover edit...

Road bridge in Manila, Philippines MacArthur BridgeMacArthur Bridge towards Santa Cruz, ManilaCoordinates14°35′41″N 120°58′53″E / 14.5947°N 120.9813°E / 14.5947; 120.9813CarriesFour lanes of N150, pedestrians and vehiclesCrossesPasig RiverLocaleManila, PhilippinesNamed forDouglas MacArthurMaintained byDepartment of Public Works and Highways – North Manila District Engineering OfficePreceded byJones BridgeFollowed byQuezon BridgeCharacteristicsDesignBeam b...

2013 British TV comedy-drama series AmbassadorsAlso known asOur MenGenreComedy-dramaWritten by James Wood Rupert Walters Directed byJeremy WebbStarring David Mitchell Robert Webb Keeley Hawes Matthew Macfadyen Velibor Topic Yigal Naor Susan Lynch Amara Karan Shivani Ghai Natalia Tena Debbie Chazen ComposerDaniel PembertonCountry of originUnited KingdomOriginal languagesEnglishRussian[1]TazbekNo. of series1No. of episodes3 (list of episodes)ProductionExecutive producers Kenton Allen Lu...

Fictional character appearing in American comic books published by Marvel Comics Not to be confused with Modem, Modum, Sodam, or Sodam Yat. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's general notability guideline. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the to...

Shopping centre in Selangor, MalaysiaJaya Shopping CentreGeneral informationTypeShopping centreLocationSection 14,Petaling Jaya, Selangor, MalaysiaConstruction started2008Completed2014Opening28 April 2014[1]OwnerMapletree InvestmentsTechnical detailsFloor area260,000 square feet (24,000 m2)Websitewww.jayashoppingcentre.my Jaya Shopping Centre was redeveloped supermarket into an approximately 260,000 square feet lifestyle mall in 2014.[2] It is located at Section 14, Petal...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2023) (Learn how and when to remove this template message) Takeover RecordsFounded1997 (1997)FounderBen HarperGenreAlternative rockPunk rockPop punkPost-hardcoreCountry of originU.S.LocationLong Beach, California Takeover Records is a punk rock record label based in Long Beach, California, United State...

Disused railway station in Shropshire, England DonningtonSite of the station in 1991General informationLocationDonnington, TelfordEnglandCoordinates52°43′32″N 2°26′05″W / 52.7256°N 2.4348°W / 52.7256; -2.4348Grid referenceSJ708143Platforms2Other informationStatusDisusedHistoryOriginal companyShropshire Union Railways and Canal CompanyPre-groupingLondon and North Western RailwayPost-groupingLondon, Midland and Scottish RailwayKey dates1 June 1849Opened1 Janu...

2016 studio album by SiaThis Is ActingStandard edition coverStudio album by SiaReleased29 January 2016Studio Echo Studio, Los Angeles, California Harmony Recording Studios, Los Angeles, California Hot Closet Studios, Los Angeles, California Kingslanding Studios, Hamptons, New York City Magical Thinking Studios, Los Angeles, California The Rib Cage, Los Angeles, California Wizard Tone Studios, Adelaide, South Australia GenrePop[1]Length46:32Label Monkey Puzzle RCA Producer Greg...

Grupo de la isla James Ross James Ross Island group Imagen fusionada de una imagen Landsat 8 OLI, y una imagen SAR Sentinel-1, adquiridas en febrero de 2017.Ubicación geográficaMar Mar de Weddell (océano Antártico)Continente AntártidaRegión península AntárticaEcorregión Ecorregión marina península antárticaCoordenadas 64°10′00″S 57°45′00″O / -64.1667, -57.75Ubicación administrativaPaís Tratado Antártico Reclamada por Argentina, Chile Chile y...

2021 single by Billie Eilish This article is about the Billie Eilish song. For the Megan Thee Stallion song, see Traumazine. NDAPromotional picture on InstagramSingle by Billie Eilishfrom the album Happier Than Ever ReleasedJuly 9, 2021Genre Alternative pop dark pop electropop industrial progressive pop Length3:16Label Darkroom Interscope Songwriter(s) Billie Eilish Finneas O'Connell Producer(s)FinneasBillie Eilish singles chronology Lost Cause (2021) NDA (2021) Happier Than Ever (2021) Music...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Knights Point – news · newspapers · books · scholar · JSTOR (October 2020) (Learn how and when to remove this template message) Knights PointPointView from Knights Point lookout to Arnott PointKnights PointLocation of Knights PointCoordinates: 43°42′45.9″S...

Makam Muhammad Saleh di kompleks Masjid Raya Air PampanMuhammad Saleh gelar Datuk Orang Kaya Besar adalah seorang pedagang Minangkabau terkemuka pada peralihan abad ke-19 dan ke-20. Muhammad Saleh lahir di Pasir Baru, Pariaman, Sumatera Barat pada tahun 1841 dan wafat pada tahun 1922.[1][2] Asal usul Mek Saleh, demikian sapaan akrabnya, lahir pada tanggal 13 Rabiul Awal 1257 Hijriyah (sekitar tahun 1841) di Dusun Pasir Baru, kini Nagari Pilubang, Kabupaten Padang Pariaman seka...

Casa de Estridsson País(es) Dinamarca, Noruega y Suecia Fundación 1047MiembrosFundador Svend II de DinamarcaÚltimo gobernante Margarita I de DinamarcaJefe actual Extinto, última monarca fue Margarita I de Dinamarca[editar datos en Wikidata] La Casa de Estridsson[1][2] fue una dinastía monárquica de Dinamarca que reinó desde 1047 hasta 1412. La dinastía lleva el nombre de su antepasado Estrid Svendsdatter. La dinastía a veces se llama el “Ulfinger”, en nomb...
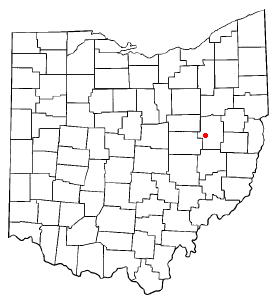
ستون كريك الإحداثيات 40°23′51″N 81°33′32″W / 40.3975°N 81.5589°W / 40.3975; -81.5589 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة تسكاراواس خصائص جغرافية المساحة 1.112634 كيلومتر مربع1.112633 كيلومتر مربع (1 أبريل 2010)[3] ارتفاع 287 مت�...




























![{\displaystyle [(8,{\frac {\pi }{3}},0,2^{-15},{\sqrt {7}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04262be6be11f68257e0dd89f45026bba3dcef03)
![{\displaystyle [(1,{\frac {\pi }{24}},0,2^{-18},{\frac {\sqrt {7}}{8}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d67cab9825d7c34e3671373f20e7b5e0b92fee66)

![{\displaystyle [({\frac {8}{\sqrt {7}}},{\frac {\pi }{3{\sqrt {7}}}},0,{\frac {2^{-15}}{\sqrt {7}}},1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/551062d88cc3c9486f1f5c7d2cba25507bce453c)






