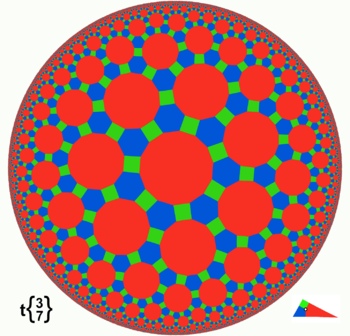
Geometría hiperbólica
|
Read other articles:

Football aux Jeux olympiques d'été de 1924 Généralités Sport Football Édition 4e Lieu(x) Paris Participants 280 (22 équipes) Épreuves 1 Palmarès Tenant du titre Belgique Vainqueur Uruguay Finaliste Suisse Troisième Suède Meilleur(s) buteur(s) Pedro Petrone (8 buts) Navigation Anvers 1920 Amsterdam 1928 modifier Le tournoi de football aux Jeux olympiques d'été de 1924 s'est déroulé du 25 mai au 9 juin 1924. Les matchs se jouent notamment au Stade Pershing à Paris. Palmarès...

WildflowerPoster resmiSutradara Matt Smukler Produser Ethan Lazar Billie Lourd Katie McNeill Kyle Owens Chris Parker Jamie Patricof Austen Rydell Dylan Sellers Ditulis oleh Jana Savage SkenarioJana SavageCerita Matt Smukler Jana Savage Pemeran Kiernan Shipka Dash Mihok Charlie Plummer Alexandra Daddario Brad Garrett Reid Scott Samantha Hyde Jacki Weaver Jean Smart Penata musikChad FischerSinematograferJeff CutterPenyuntingJC BondPerusahaanproduksi eOne Limelight Morning Moon Hunting Lan...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2023) (Learn how and when to remove this template message) 1985 sports video game 1985 video gameFinal Four College BasketballPublisher(s)Lance Haffner GamesPlatform(s)Apple II, Commodore 64, Atari 8-bit familyRelease1985Genre(s)SportsFinal Four College Basketball is a video game published in 1985 by L...

This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Bizou TV series – news · newspapers · books · scholar · JSTOR (January 2011) (Learn how and when to remove this template message) Bizou is a 2007 Canadian Flash animated preschool television series. It teaches children about animals and Aboriginal life through the eyes of an Aboriginal princess named ...

Village and civil parish in the East Lindsey district of Lincolnshire, England This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chapel St Leonards – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Human settlement in EnglandChapel St LeonardsThe...

2012 promotional single by Nicki Minaj featuring Lil WayneRoman ReloadedPromotional single by Nicki Minaj featuring Lil Waynefrom the album Pink Friday: Roman Reloaded ReleasedFebruary 24, 2012Recorded2011GenreHardcore hip hopLength3:14LabelYoung MoneyCash MoneyUniversal RepublicSongwriter(s)Onika MarajDwayne CarterRicardo LamarreProducer(s)Rico Beats Roman Reloaded is a song by rapper Nicki Minaj featuring Lil Wayne, from Minaj's second studio album Pink Friday: Roman Reloaded. After being p...

Season of television series Strike the Blood IVThe cover of the first Blu-ray compilation of the fourth season released by Warner Home Video.Country of originJapanNo. of episodes12ReleaseOriginal releaseApril 8, 2020 (2020-04-08) –June 30, 2021 (2021-06-30)Season chronology← PreviousStrike the Blood III Next →Strike the Blood Final List of episodes Strike the Blood is an anime series adapted from the light novel series of the same title written by Gakuto Mikumo ...

У Вікіпедії є статті про інших людей із прізвищем Герберт.Браян ГербертBrian Herbert Браян ГербертІм'я при народженні Браян Патрік ГербертНародився 29 червня 1947(1947-06-29) (76 років)Сієтл, штат ВашингтонГромадянство СШАДіяльність прозаїк-романіст, письменник, письменник на�...

Archaic conception of Earth's shape This article is about the disproven cosmological model. For modern-day beliefs that the Earth is flat, see Modern flat Earth beliefs. For the historical misconception that people during the Middle Ages believed that the Earth was flat, see Myth of the flat Earth. For other uses, see Flat Earth (disambiguation). The examples and perspective in this article deal primarily with Europe in the lede and do not represent a worldwide view of the subject. You may im...

Wales based men's choir Members of the choir in blazer and tie awaiting a bus (2008) Treorchy Male Choir, also known as Treorchy Male Voice Choir, is a choir based in Treorchy in the Rhondda Valley, Wales, United Kingdom. History Choirs have existed in the Rhondda Valley for more than a 150 years and Treorchy is one of the best known from the area. One of its first male choirs was formed in the Red Cow Hotel in the summer of 1883[1] and developed into a National Eisteddfod winner, cul...

Spanish cyclist Joan LlanerasLlaneras in 2011Personal informationFull nameJoan Llaneras RossellóBorn (1969-05-17) 17 May 1969 (age 54)Porreres, SpainHeight5 ft 11 in (1.80 m)Weight143 lb (65 kg)[1]Team informationDisciplineTrackRoleRiderRider typeMadison and pointsProfessional teams1991–1995ONCE1998U.S. Postal Service Medal record Representing Spain Men's track cycling Olympic Games 2000 Sydney Points race 2008 Beijing Points race 2...

Major highway in Brazil BR-230 Trans-Amazonian HighwayMap of BR-230 (paved portion shown in red)[1]Trans-Amazonian highway within the city of Pombal, Paraíba.LocationCountryBrazil Highway system Highways in Brazil Federal The Trans-Amazonian Highway (official designation BR-230, official name Rodovia Transamazônica), was introduced on September 27, 1972. It is 4,000 km long, making it the third longest highway in Brazil. It runs through the Amazon forest and the Brazilian state...

American actor Eric CloseClose at the 16th Annual MovieGuide Faith and Values Awards in 2008BornEric Randolph Close (1967-05-24) May 24, 1967 (age 56)Staten Island, New York, United StatesAlma materUniversity of Southern California (BA)OccupationActorYears active1991–presentSpouseKeri Close (m. 1995)Children2 Eric Randolph Close (born May 24, 1967) is an American actor, best known for his roles in television series, particularly as FBI agent Martin Fitzgerald in the CBS m...

Portable vault first featured in The Da Vinci Code This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cryptex – news · newspapers · books · scholar · JSTOR (February 2019) (Learn how and when to remove this template message) Replica cryptex: prize from Google Da Vinci Code Quest Contest The word cryptex is a ne...

Questa voce sull'argomento hockeisti su ghiaccio svedesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Henry Johansson Nazionalità Svezia Hockey su ghiaccio Palmarès Competizione Ori Argenti Bronzi Giochi olimpici 0 1 0 Per maggiori dettagli vedi qui Modifica dati su Wikidata · Manuale Henry Johan Johansson (Södertälje, 23 settembre 1897 – Södertälje, 28 maggio 1979) è stato un hockeista su ghiaccio svedese. Palmarès Olim...

Эта статья написана в рекламном стиле. Это не соответствует правилам Википедии. Вы можете помочь проекту, исправив текст согласно стилистическим рекомендациям Википедии. Tizen Разработчик Linux Foundation, Tizen Association, Intel, Samsung[1] Семейство ОС Linux Исходный код открытое программн�...

Jaime Lannister Personaje de Canción de hielo y fuego Cosplayer interpretando al personaje derrotando a un enemigo.Primera aparición A Game of Thrones (libro)Winter is Coming (serie)Última aparición The Iron Throne (serie)Creado por George R. R. MartinInterpretado por Nikolaj Coster-WaldauDoblador en España Miguel Ángel MonteroDoblador en Hispanoamérica Ricardo MéndezEpisodios 55Temporada(s) 1, 2, 3, 4, 5, 6, 7, 8Información personalEstatus actual Vivo (libros) Muerto (serie)Alias Ma...

For broader coverage of this topic, see Rotation group SO(3). This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Charts on SO(3) – news · newspapers · books · scholar · JSTOR (May 2021) In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO(3), is a ...

This article is about the cancelled sequel to Prey (2006 video game). For the 2017 game, see Prey (2017 video game). Video gamePrey 2Developer(s)Human Head StudiosPublisher(s)Bethesda SoftworksDirector(s)Chris RhinehartDesigner(s)Ben GokeyTed HalstedNathan CheeverProgrammer(s)Paul MacArthurArtist(s)James SumwaltRandy RedetzkeWriter(s)Jason L. BlairComposer(s)Jason GravesMark MorganEngineid Tech 4Platform(s)Microsoft Windows, PlayStation 3, Xbox 360ReleaseCancelledGenre(s)First-person shooterM...

У этого термина существуют и другие значения, см. Сале (значения). Жами Сале Сале в 2010 году. Персональные данные Гражданство Канада Дата рождения 21 апреля 1977(1977-04-21) (46 лет) Место рождения Калгари Рост 155 см Партнёр Давид Пеллетье Бывшиепартнёры Джейсон Тёрнер Тренер Ришар Г�...