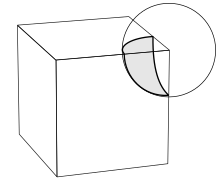
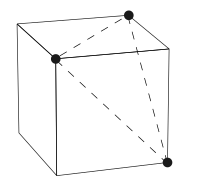
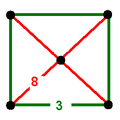
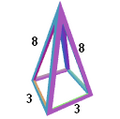
Vertex figure
|
Read other information related to :Vertex figure/
Vertex Vertex cover Vertex (geometry) Vertex (graph theory) Vertex operator algebra Vertex Pharmaceuticals Vertex figure Vertex configuration Vertex (company) Eight-vertex model Universal vertex Vertex (computer graphics) Vertex normal Vertex Holdings Vertex (album) Vertex Resource Group Vertex, Inc. Four-vertex theorem Vertex-transitive graph Vertex separator Vertex function Vertex buffer object Vertex enumeration problem K-vertex-connected graph Table of vertex-symmetric digraphs 110-vertex Iofinova–Ivanov graph Vertex arrangement Vertex cycle cover Vertex angle Edge and vertex spaces Vert…
ex (anatomy) Vertex model Vertex distance Vertex United Vertex Railcar Edge contraction Vértex Vinter Isogonal figure Vertex painting Ice-type model Vertex (curve) Vertex cover in hypergraphs Vertex (band) Biconnected component Vertex pipeline Newest vertex bisection Monster vertex algebra List of uniform polyhedra by vertex figure Feedback vertex set Morph target animation Shader Link (simplicial complex) National Arts Holdings Degree (graph theory) Slow vertex response Adjacent-vertex-distinguishing-total coloring Graph labeling Vertex k-center problem Independent set (graph theory) Prototroctes vertex Neighbourhood (graph theory) Graph coloring Pancyclic graph Distance (graph theory) Glossary of graph theory Handshaking lemma Vertex of a representation Abstract polytope Path (graph theory) Cycle rank Cephalic presentation Lie-* algebra N-dimensional polyhedron Maximal independent set Expander graph List of small polyhedra by vertex count Line graph Vertexguy Interaction point Matching (graph theory) Graph operations Lunar swirls Glossary of computer graphics Graphics pipeline Cut (graph theory) Steiner tree problem Feynman diagram Completing the square Greedoid Fjällmaraton Po
Read other articles:

Details of the trade planning and execution by India Part of a series onWorld trade Policy Import Export Balance of trade Trade law Trade pact Trade bloc Trade creation Trade diversion Export orientation Import substitution Trade finance Trade facilitation Trade route Domestic trade Tax Restrictions Trade barriers Tariffs Non-tariff barriers Import quotas Tariff-rate quotas Import licenses Customs duties Export subsidies Technical barriers Bribery Exchange rate controls Embargo Safeguards Counte…

Існує декілька осіб з таким іменем та прізвищем. Ця сторінка значень містить посилання на статті про кожну з них.Якщо ви потрапили сюди за внутрішнім посиланням, будь ласка, поверніться та виправте його так, щоб воно вказувало безпосередньо на потрібну статтю.@ пошук посил

View of Egmond aan ZeeArtistJacob van RuisdaelYear1650sDimensions31 cm × 35 cm (12 in × 14 in)LocationNationalmuseum, Stockholm View of Egmond aan Zee (c. 1650s) is an oil on canvas painting by the Dutch landscape painter Jacob van Ruisdael.[1] It is an example of Dutch Golden Age painting and is now in the collection of the Nationalmuseum in Stockholm. This painting was documented by Hofstede de Groot in 1911, who wrote; 50. VIEW OF EGMOND AAN…

Olga SafronovaSafronova pada Kejuaraan Asia 2017Informasi pribadiLahir5 November 1991 (umur 32)Karaganda, Kazakhstan[1]PendidikanPelatihanAlma materUniversitas Negeri Karaganda[2]Tinggi172 m (564 ft 4 in)[2]Berat65 kg (143 pon) OlahragaDilatih olehYury MashtakovAlexander Denisko (personal)[2][3]Prestasi dan gelarOlimpiadeLondon 2012 (semifinal)Peringkat pribadi terbaik100 m – 11.09 (2016)200 m – 22.85 (2014)[4] Rek…

German chemist (1892-1969) Walter ReppeBorn29 July 1892Göringen, German EmpireDied26 July 1969(1969-07-26) (aged 76)Heidelberg, West GermanyAlma materUniversity of JenaUniversity of MunichKnown forchemistry of acetyleneAwardsWerner von Siemens Ring (1960)Scientific careerFieldsChemistryInstitutionsBASFUniversity of MainzTH Darmstadt Walter Julius Reppe (29 July 1892 in Göringen – 26 July 1969 in Heidelberg) was a German chemist. He is notable for his contributions to the chemi…

神明社 所在地 東京都世田谷区祖師谷5-1-7主祭神 天照皇大神社格等 村社創建 不詳別名 下祖師谷神明社テンプレートを表示 神明社(しんめいしゃ)は、東京都世田谷区の神社。 歴史 創建年代は不明である。喜多見氷川神社が所有する当社の由緒によれば、新田義興・義宗兄弟が当社で戦勝祈願したという[1]。 1873年(明治6年)、近代社格制度における「村社」とな�…

Hotel and casino in Atlantic city For the village in Hungary, see Borgáta. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Borgata – news · newspapers · books · scholar · JSTOR (January 2018) (Learn how and when to remove this template message) Borgata Hotel Casino & SpaBorgata and The Water Club Location …

1919 silent film HeartseaseTrade advertisementDirected byHarry BeaumontWritten byEdfrid A. BinghamBased onHeartseaseby Joseph I.C. Clarke and Charles KleinStarringTom MooreHelene ChadwickLarry SteersCinematographySam LandersProductioncompanyGoldwyn PicturesDistributed byGoldwyn DistributingRelease date August 24, 1919 (1919-08-24) Running time50 minutesCountryUnited StatesLanguageSilent (English intertitles) Heartsease is a 1919 American silent drama film directed by Harry Beaumon…

إم بي دي إيهالشعارمعلومات عامةالجنسية فرنسا[1] التأسيس 2001النوع منظمة الشكل القانوني شركة بأسهم مبسطة[2] المقر الرئيسي المملكة المتحدة، باريس، فرنسا، روما، إيطاليا، شروبنهاوزن، ألمانياموقع الويب mbda-systems.com المنظومة الاقتصاديةالشركات التابعة MBDA (United Kingdom) (en) MBDA Deutschland…

Studio album by Nena Feuer und FlammeStudio album by NenaReleased24 June 1985 (1985-06-24)Recorded1984–1985StudioSpliff Studio, West BerlinGenreNDW, pop rock, popLength46:11 (CD)44:08 (LP)LanguageGermanLabelCBSProducerReinhold HeilNena chronology 99 Luftballons(1984) Feuer und Flamme(1985) It's All in the Game(1985) Singles from Feuer und Flamme Irgendwie, irgendwo, irgendwannReleased: 1984 Feuer und FlammeReleased: 1985 Haus der drei SonnenReleased: 1985 Jung wie duReleased…

Antoninian des Aemilianus, auf dem der Kriegsgott Mars als Friedensstifter dargestellt wird. Marcus Aemilius Aemilianus (kurz Aemilian; * 207 oder 213 in Djerba; † 253) war im Jahr 253 römischer Kaiser. Inhaltsverzeichnis 1 Leben 2 Literatur 3 Weblinks 4 Anmerkungen Leben Cornelia Supera, Gattin des Aemilianus Aemilianus wurde entweder 207 oder 213 im afrikanischen Djerba geboren; nach dem mittelbyzantinischen Historiker Johannes Zonaras war er ein Libyer. Seine Frau hieß Cornelia Supera, ü…

Swiss woman executed for witchcraft This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (October 2022) You can help expand this article with text translated from the corresponding article in French. (September 2022) Click [show] for i…

For other films of this title, see Bloodsucker (disambiguation). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2010) (Learn how and when to remove this template message) Canadian TV series or program BloodsuckersWritten byMatthew HastingsDirected byMatthew HastingsStarringDominic ZamprognaA.J. CookNatassia MaltheTheme music composerDavor VulamaCountr…

Oliver E. WilliamsonOliver Eaton Williamson (2009)Kebangsaan Amerika SerikatInstitusiUniversity of California, BerkeleyBidangEkonomi mikroMazhabEkonomiAlma materStanfordMITCarnegie Mellon UniversityDipengaruhiRonald CoaseHerbert SimonRichard CyertIan Roderick MacneilPenghargaanPenghargaan Nobel dalam Ekonomi (2009) Oliver E. Williamson (lahir 27 September 1932) adalah seorang ahli ekonomi dari University of California, Berkeley, Amerika Serikat yang diumumkan sebagai penerima Pengharga…

وسط الاستوائية علم الاسم الرسمي (بالإنجليزية: Central Equatoria) الإحداثيات 4°20′47″N 31°12′04″E / 4.346389°N 31.201111°E / 4.346389; 31.201111 [1] تقسيم إداري البلد جنوب السودان[2] التقسيم الأعلى جنوب السودان العاصمة جوبا خصائص جغرافية المساحة 43033.00 �…

List of events ← 1917 1916 1915 1918 in Australia → 1919 1920 1921 Decades: 1890s 1900s 1910s 1920s 1930s See also: Other events of 1918 Timeline of Australian history 1918 in AustraliaMonarchGeorge VGovernor-GeneralRonald Munro-FergusonPrime ministerBilly HughesPopulation5,029,403ElectionsSouth Australia, Queensland 1918 in Australia was dominated by national participation in World War I. The Australian Corps, formed at the beginning of the year from the five divisions of the First …

British folklorist Dr. Agnes Murgoci (1875 – 7 May 1929), was an Australian born, English zoologist and folklorist. Agnes Kelly (later Murgoci) was born in Adelaide, South Australia in 1875, the daughter of Adam Kelly, formerly of Glasgow, and Helen Beveridge. Her parents returned to England with Agnes, when she was three years old. Kelly attended school at Dollar Academy and entered Bedford College in 1892. She graduated in 1896, obtaining her B.Sc. with first class honours in zoology. She mo…

Japanese video game developer For other uses, see Omega Force (disambiguation). Omega ForceNative nameオメガフォースTypeDivisionIndustryVideo gamesFounded1996; 27 years ago (1996)FounderAkihiro SuzukiKenichi OgasawaraHeadquartersAshikaga, Tochigi, JapanKey peopleTomohiko Sho (president)[1]ProductsDynasty Warriors series Samurai Warriors series One Piece: Pirate Warriors seriesParentKoei (1996–2010)Koei Tecmo (2010–present) Omega Force (Japanese: オメガフ�…

Ospedale di San Giacomo in AugustaLato sud della struttura, lungo via Canova (già via San Giacomo, fino al 1914). A fronte dell'edificio è situato l'atelier dell'omonimo scultore.LocalizzazioneStato Italia RegioneLazio LocalitàRoma IndirizzoVia Canova 29, via del Corso tra 493 e 497 Coordinate41°54′26.68″N 12°28′37.67″E / 41.90741°N 12.47713°E41.90741; 12.47713Coordinate: 41°54′26.68″N 12°28′37.67″E / 41.90741°N 12.47713°E41.90741; …

Modern English translation of the Bible Not to be confused with Legacy Standard Bible or Literal English Version. Literal Standard VersionFull nameLiteral Standard VersionAbbreviationLSVComplete Biblepublished2020Online asLiteral Standard Version at WikisourceDerived fromYLTTextual basisMasoretic Text, Septuagint, Dead Sea Scrolls, Textus Receptus, other New Testament manuscripts consultedTranslation typeFormal EquivalenceReading levelHigh SchoolPublisherCovenant PressCopyrightRegister…