Geordnete abelsche Gruppe
|
Read other articles:

Talsperre Neustadt / Neustädter Talsperre(Nordhäuser Talsperre) Luftseite der Staumauer (2007) Luftseite der Staumauer (2007) Lage Harz, Landkreis Nordhausen, Thüringen, Deutschland Zuflüsse Krebsbach Abfluss Krebsbach → Thyra Größere Orte in der Nähe Neustadt/Harz Talsperre Neustadt / Neustädter Talsperre(Nordhäuser Talsperre) (Thüringen) Thüringen, Deutschland Koordinaten 51° 34′ 50″ N, 10° 52′ 2″ O51.58055555555610.867222222222Koordinate...

Hanjin Shipping Co. LtdNama asli한진해운IndustriPeti kemas, pengapalan, transportasi kargo lautNasibKebangkrutan, likuidasiDidirikan16 Mei 1977 (1977-05-16)Ditutup17 Februari 2017 (2017-2-17)KantorpusatKorea SelatanJasaPengapalan, bongkar muat, manajemen terminal peti kemasPemilikHanjinIndukKorean Air (43,26%)Situs webhanjin.com Hanjin Shipping Co., Ltd. dulunya adalah sebuah perusahaan transportasi peti kemas dan logistik terintegrasi asal Korea Selatan. Sebelum mengalami masal...

Burosse-Mendousse Burosse-Mendousse (Frankreich) Staat Frankreich Region Nouvelle-Aquitaine Département (Nr.) Pyrénées-Atlantiques (64) Arrondissement Pau Kanton Terres des Luys et Coteaux du Vic-Bilh Gemeindeverband Luys en Béarn Koordinaten 43° 31′ N, 0° 13′ W43.5128-0.210555555556Koordinaten: 43° 31′ N, 0° 13′ W Höhe 142–283 m Fläche 5,62 km² Einwohner 72 (1. Januar 2020) Bevölkerungsdichte 13 Einw./km² Postleitz...

Колодіївка Коростенська дирекція Південно-Західна залізниця зупинний пунктРозташуванняРозташування 1 км від с.ЯсногіркаКоординати 50°21′54″ пн. ш. 28°21′34″ сх. д. / 50.36500000002777711° пн. ш. 28.359700000028° сх. д. / 50.36500000002777711; 28.359700000028Координати: 50°21′54�...

「ラプターズ」はこの項目へ転送されています。日本のベースボール・チャレンジ・リーグに所属する野球チームについては「福井ワイルドラプターズ」をご覧ください。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: トロント・ラプター

MuskovitMuskovit dengan albit dari lembahDoce , Minas Gerais, Brazil (dimensi: 6×5.3×3.9 cm)UmumKategorimineral filosilikatRumus kimiaKAl2(AlSi3O10)(F,OH)2Klasifikasi Strunz09.EC.15Klasifikasi Dana71.02.02a.01Simetri kristal2/m – prismatikSel unita = 5.199 Å, b = 9.027 Å, c = 20.106 Å, β = 95.78°; Z = 4IdentifikasiWarnaPutih, abu-abu, silverPerawakanMasif hingga lempengSistem kristalMonoclinic (2/m), space group C 2/mBentuk kembaranCommon on the [310], less common on the {001}Belahan...

CatshuisCatshuisInformasi umumKotaDen HaagNegaraBelandaMulai dibangun6 Mei 1651; 372 tahun lalu (1651-05-06)KlienJacob CatsDesain dan konstruksiArsitekPieter Post dari Lodewijk HuygensTeknisiJacob Cats Catshuis adalah kediaman resmi Perdana Menteri Kerajaan Belanda sejak 1963. Bangunan ini terletak di ibu kota pemerintahan Den Haag, tepatnya di tengah jalan menuju Scheveningen. Rumah ini digunakan untuk menyambut tamu resmi. Sejarah Rumah ini dulunya bernama Huis Sorgvliet dan dibangun d...

Академія медичних наук СРСР Основні дані Засновано 1944 Країна СРСРТип академія наук і організаціяМатеринськаорганізація Академія наук СРСР Акаде́мія меди́чних нау́к СРСР — вища наукова медична установа в СРСР. Створена в 1944 році. ЇЇ приємниками є Російська А�...

Defunct American soccer club Soccer clubCalifornia SurfFull nameCalifornia SurfNickname(s)The SurfFounded1978Dissolved1981StadiumAnaheim Stadium 69,008 Indoor:Anaheim Convention Center 5,400 (1979–80)Long Beach Arena 10,600 (1980–81)LeagueNorth American Soccer League Home colors Away colors The California Surf was an American soccer team that competed in the North American Soccer League (NASL) from 1978 to 1981. The team was based in Anaheim, California and played their home games at Anah...
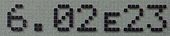
Method of writing numbers with a large amount of digits This article is about a numeric notation. For the musical notation, see Scientific pitch notation. E notation redirects here. For the series of preferred numbers, see E series. For the food additive codes, see E number. Scientific notation is a way of expressing numbers that are too large or too small to be conveniently written in decimal form, since to do so would require writing out an inconveniently long string of digits. It may be re...

You can help expand this article with text translated from the corresponding article in Bulgarian. (June 2023) Click [show] for important translation instructions. View a machine-translated version of the Bulgarian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wik...

The Gurkha divisions are preparing defensive positions, July 1915 A defensive zone is a previously prepared area of terrain allocated for defense to a military formation, where its forces and means are located, a fire system is organized, engineering barriers and fortifications are erected.[1][2] The defensive zone from the front is limited by the front line, from the flanks – by demarcation lines with neighboring units, and from the rear – by the depth of the battle forma...

غيسلين ماكسويل (بالفرنسية: Ghislaine Maxwell) معلومات شخصية اسم الولادة (بالفرنسية: Ghislaine Noelle Marion Maxwell) الميلاد 25 ديسمبر 1961 (62 سنة)[1] ميزون-لافيت الإقامة بلغرافيا مواطنة المملكة المتحدة[2] الولايات المتحدة (2002–)[2] فرنسا[2] العشير جيفري إبستاي...

Bang và lãnh thổ liên bang của Ấn Độ Andhra Pradesh Arunachal Pradesh Assam Bihar Chhattisgarh Lãnh thổ Thủ đô Quốc gia Delhi Goa Gujarat Haryana Himachal Pradesh Jammu và Kashmir Jharkhand Karnataka Kerala Madhya Pradesh Maharashtra Manipur Meghalaya Mizoram Nagaland Orissa Punjab Rajasthan Sikkim Tamil Nadu Tripura Uttarakhand Uttar Pradesh Tây Bengal Quần đảoAndamanvàNicobar Chandigarh Dadra và Nagar Haveli Daman và Diu Lakshadweep Puducherry <maplink>:...

Tail of an ox Raw oxtail Southern oxtail soup Oxtail (occasionally spelled ox tail or ox-tail) is the culinary name for the tail of cattle. While the word once meant only the tail of an ox, today it can also refer to the tails of other cattle.[1] An oxtail typically weighs around 3.5 kilograms (8 pounds) and is skinned and cut into shorter lengths for sale. Oxtail is a gelatin-rich meat, which is usually slow-cooked as a stew[2] or braised. It is a traditional stock base for o...

American basketball player (born 1993) Treveon GrahamGraham with the Brooklyn Nets in 2018No. 21 – Motor City CruisePositionShooting guard / small forwardLeagueNBA G LeaguePersonal informationBorn (1993-10-28) October 28, 1993 (age 30)Washington, D.C., U.S.Listed height6 ft 5 in (1.96 m)Listed weight219 lb (99 kg)Career informationHigh schoolSt. Mary's Ryken(Leonardtown, Maryland)CollegeVCU (2011–2015)NBA draft2015: undraftedPlaying career2015–prese...

Type of priest For other uses, see Vicar (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vicar – news · newspapers · books · scholar · JSTOR (December 2008) (Learn how and when to remove this template message) A vicar (/ˈvɪkər/; Latin: vicarius) is a representative, deputy or substitute;...

Questa voce sull'argomento ciclisti italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Mario Lusiani Nazionalità Italia Ciclismo Specialità Strada, Pista Termine carriera 1934 Carriera Squadre di club 1927 Bianchi1928-1932Individuale1933U.S. Ausonia Torino1934C. Battisti Milano Nazionale 1928 Italiapista Palmarès Giochi olimpici Oro Amsterdam 1928 Ins. a squadre Statistiche agg...

1940 film ArgilaDirected byHumberto MauroScreenplay byHumberto MauroProduced byCarmen SantosCinematographyHumberto Mauro, Manoel RibeiroEdited byHippólito Collomb, Watson MacedoMusic byRadamés Gnatalli, Edgar Roquette-Pinto, Heckel TavaresProductioncompanyBrasil Vita FilmesRelease date1940Running time103 minutesCountryBrazilLanguagePortuguese Argila is a 1940 Brazilian romantic drama film directed by Humberto Mauro and starring Carmen Santos, Celso Guimarães, and Lídia Mattos.[1] ...

Census-designated place in Pennsylvania, United StatesBroomall, PennsylvaniaCensus-designated placeThomas Massey HouseLocation in Delaware County and the U.S. state of Pennsylvania.Coordinates: 39°58′18″N 75°21′17″W / 39.97167°N 75.35472°W / 39.97167; -75.35472CountryUnited StatesStatePennsylvaniaCountyDelawareTownshipMarpleArea[1] • Total3.17 sq mi (8.21 km2) • Land3.17 sq mi (8.21 km2) •...



































































































![{\displaystyle [x]\leq [y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a78f45c685464633e52a4ca73a1bbc7e7f0ca480)

