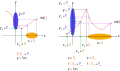Surjective function
|
Read other articles:

徳島県立富岡西高等学校 北緯33度55分8.53秒 東経134度39分0.58秒 / 北緯33.9190361度 東経134.6501611度 / 33.9190361; 134.6501611座標: 北緯33度55分8.53秒 東経134度39分0.58秒 / 北緯33.9190361度 東経134.6501611度 / 33.9190361; 134.6501611過去の名称 徳島県尋常中学校第二分校徳島県富岡中学校徳島県立富岡中学校徳島県富岡第一高等学校徳島県富岡西高等学校国公私

2001 studio album by Secret Chiefs 3Book MStudio album by Secret Chiefs 3Released11 September 2001 (2001-09-11)Recorded2001 (2001)Studio Various Coast Recorders (San Francisco, CA) Feast or Famine (San Francisco, CA) Littlefield Pipe Organ Chamber (San Diego, CA) Mills College (Oakland, CA) Rohypnol Studios (London, UK) Found Sound (San Francisco, CA) GenreExperimental rockLength54:58LabelWeb of MimicryProducerTrey SpruanceSecret Chiefs 3 chronology Eyes of Flesh, ...

Existen dudas o desacuerdos sobre la exactitud de la información en este artículo o sección. Consulta el debate al respecto en la página de discusión.Uso de esta plantilla: {{Discutido|t={{sust:CURRENTTIMESTAMP}}}} o {{sust:Discutido}} Mapa indicando la corriente Ecuatorial del Norte en el Atlántico, Pacífico, pero variable en el Índico debido al monzón. La corriente Ecuatorial del Norte o corriente Norecuatorial es una significativa corriente marina cálida de los océanos Pacífico...

The Electric BoyEpisode Cosmos: A Spacetime OdysseyNomor episodeEpisode 10SutradaraBrannon BragaPenulisAnn DruyanSteven SoterNaratorNeil deGrasse TysonProduserLivia HanichSteven HoltzmanMusikAlan SilvestriPenyuntingJohn DuffyMichael O'HalloranEric LeaTanggal siar11 Mei 2014 (2014-05-11)Durasi42 menitBintang tamu Kronologi episode ← SebelumnyaThe Lost Worlds of Planet Earth Selanjutnya →The Immortals Daftar episode Cosmos: A Spacetime Odyssey The Electric Boy adalah episode ...

Questa voce sugli argomenti Nazionali di football americano e sport negli Stati Uniti d'America è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Stati Uniti d'America Campione del mondo in carica Uniformi di gara Divisa casalinga Sport Football americano Federazione USA Football/USFAF Confederazione IFAF Americas Soprannome Team USA Head coach John Mackovic Top scorer Craig Coffin (28) Sito www.usafootball.com Esordio internazionale Francia 0 - 28 Stati...

الحديقة أو الحدائق اليابانية (باليابانية: 日本庭園) هي البساتين التي يتم العناية بها في اليابان حسب الطرق التقليدية، وتقوم هذه الطرق على فن خاص يعود تاريخه إلى العهود القديمة. يمكن العثور على هذه الحدائق في بعض البيوت التقليدية اليابانية، في الحدائق العمومية، في المعابد البو

Сен-Донан, Сен-Дона́н (фр. Saint-Donan) — муніципалітет у Франції, у регіоні Бретань, департамент Кот-д'Армор. Замок Ейлен-Донан (шотл. гел. Eilean Donan, у перекладі «Острів Донана») — замок, розташований на скелястому острові, що у фіорді Лох-Дуйх у Шотландії. Ейлін Донан (англ. Eilean Donan, ш

Дебьоський район рос. Дебёсский районудм. Дэбес ёрос Герб Дебьоського району Прапор Дебьоського району Основні дані Суб'єкт Російської Федерації: Удмуртія Утворений: 15 липня 1929 року Населення (2019[1]): 11842 особи Площа: 1033,03 км² Густота населення: 11,46 осіб/км² Населе�...

Secucinumab, com o nome comercial Cosentyx, é um anticorpo monoclonal humano produzido pela Novartis para o tratamento da psoríase. Este fármaco foi também aprovado para o tratamento da artrite psoriática e da espondilite anquilosante. O secucinumab atua por inibição seletiva da interleucina 17-A (IL-17A), uma citocina pró-inflamatória.[1] Como consequência, o tratamento com secuquinumab reduz o eritema, o endurecimento e a descamação presentes na psoríase em placas. Referê...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Music history of the United States – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) This article is part of a series on theMusic of the United StatesChicago, a 1975 American musical with music by...

Jos Wagner (Antwerpen, 2 december 1914 - Aartselaar, 8 januari 2007) was een Belgisch voetballer. Hij was een rasechte Antwerpenaar,in zijn jeugd straatvoetbal spelend,eerst aan de Ossemarkt, daarna op het Kiel. Hij speelde eerst een tijd in de lagere reeksen, onder andere bij Nielse FC. In 1937, echter, was FC Antwerp verscheurd door de rebellen, omwille van onverenigbare meningsverschillen tussen bestuur en bepaalde spelers dewelke vertrokken naar een andere liga. Wagner werd gespot en aang...

American public high school This article uses bare URLs, which are uninformative and vulnerable to link rot. Please consider converting them to full citations to ensure the article remains verifiable and maintains a consistent citation style. Several templates and tools are available to assist in formatting, such as reFill (documentation) and Citation bot (documentation). (August 2022) (Learn how and when to remove this template message) Sequoyah High SchoolLocation3128 Hwy 411, Madisonville,...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Gempa bumi Illinois 1968 – berita · surat kabar · buku · cendekiawan · JSTOR Gempa Bumi Illinois 1968Waktu UTC??ISCUSGS-ANSSTanggal *9 November 1968 (1968-11-09)Tanggal setempatWaktu&...

American politician (1792–1877) For the American real estate developer, see Charles Dayan (real estate developer). Charles DayanDistrict attorney (Lewis Co.)In office1840–1845New York State Assembly (Lewis Co.)In office1835–1836Member of the U.S. House of Representativesfrom New York's 20th districtIn officeMarch 4, 1831 – March 3, 1833Preceded byJonah SanfordJoseph HawkinsSucceeded byNoadiah JohnsonActing Lieutenant Governor of New YorkIn officeOctober 17, 1828&#...

American politician Thomas M. PaschalMember of the U.S. House of Representativesfrom Texas's 12th districtIn officeMarch 4, 1893 – March 3, 1895Preceded byDistrict createdSucceeded byGeorge H. Noonan Personal detailsBornThomas Moore Paschal(1845-12-15)December 15, 1845Alexandria, Louisiana, U.S.DiedJanuary 28, 1919(1919-01-28) (aged 73)New York City, U.S.Resting placeMission Burial Park, San Antonio, Texas, U.S.Political partyDemocraticAlma materSt. Mary's CollegeC...

Comune in Piedmont, ItalyCortazzoneComuneComune di Cortazzone Coat of armsLocation of Cortazzone CortazzoneLocation of Cortazzone in ItalyShow map of ItalyCortazzoneCortazzone (Piedmont)Show map of PiedmontCoordinates: 44°59′N 8°4′E / 44.983°N 8.067°E / 44.983; 8.067CountryItalyRegionPiedmontProvinceAsti (AT)FrazioniBriccarello, Mongiglietto, Valmezzana, VanaraGovernment • MayorFrancesco ChiaraArea[1] • Total10.4 km2 (4....

Light novel based on Neon Genesis Evangelion Neon Genesis Evangelion: AnimaCover of the first English novel volumeエヴァンゲリオン ANIMA(Evangerion ANIMA)Created byKhara Light novelWritten byTakuma Kageyama (2008)Ikuto Yamashita (2009–13)Illustrated byIkuto YamashitaPublished byKadokawa ShotenEnglish publisherNA: Seven Seas EntertainmentMagazineDengeki HobbyDemographicMaleOriginal runJanuary 2008 – January 2013Volumes5 (List of volumes) Neon Genesis Evangelion:...

2010 British filmDance StarShe Is The One...Directed bySteven M. SmithWritten bySteven M. SmithProduced bySteven M. SmithKeeley ScottStarringBruce PayneVivien CreegorJon-Paul GatesMegan LittleCinematographyKirk GaydonEdited byBarry LuptonMusic byBarry A. E. CovellDistributed byGreenway Entertainment Amazon rentalRelease date 7 March 2010 (2010-03-07) Running time91CountryUnited KingdomLanguageEnglish Dance Star is a 2010 British dance musical film set in Essex, UK. It was writt...

Katedral KalocsaKatedral Metropolitan Santa Perawan Maria Diangkat ke Surgabahasa Hungaria: Nagyboldogasszony FőszékesegyházKatedral KalocsaLokasiKalocsaNegara HungariaDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupan AgungKeuskupan Agung Kalocsa-Kecskemét Katedral Bunda Maria Diangkat ke Surga [1] (bahasa Hungaria: Nagyboldogasszony Főszékesegyház) disebut juga Katedral Kalocsa[2] adalah sebuah gereja katedral...

2002 single by SweetboxHere On My Own(Lighter Shade Of Blue)Single by Sweetboxfrom the album Jade B-sideOne Kiss (Acoustic Version)Released2002GenrePopLength3:35 (European version/Single version)3:49 (Japanese album version)LabelWarner Music GroupSongwriter(s)Geoman, VillalonProducer(s)GeomanSweetbox singles chronology Read My Mind (2002) Here On My Own(Lighter Shade Of Blue) (2002) Life Is Cool (2004) Here on My Own (Lighter Shade Of Blue) is the second single by Sweetbox from the album Jade...