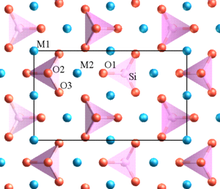
Pauling's rules
|
Read other articles:

Евреи в Казахстане (каз. Қазақстандағы еврейлер) — группа населения, являющаяся этническим меньшинством страны. Содержание 1 История 1.1 Дореволюционная история 1.2 Довоенный период 1.3 Война и эвакуация 1.4 Послевоенное время 1.5 80-е годы — наши дни 2 Известные казахстанские ев

Pandit Bhimsen JoshiInformasi latar belakangNama lahirPandit Bimsen JoshiLahir(1922-02-04)4 Februari 1922Ron, Karnataka, IndiaMeninggal24 Januari 2011(2011-01-24) (umur 88)Pune, MaharashtraGenreMusik klasik HindustaniPekerjaanPenyanyi RaagTahun aktif1941–2000Situs webTanda tangan Pt. Bhimsen Joshi Bhimsen Gururaj Joshi (pengucapanⓘ);[1] 4 Februari 1922 – 24 Januari 2011) adalah seorang vokalis India dari Karnataka dalam tradisi klasik Hindustani. Ia dikenal karena bentuk me...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (نوفمبر 2018) روبن دوق معلومات شخصية الميلاد 13 مارس 1954 (69 سنة) سانت كاثرينز مواطنة كندا الطول 1.65 متر الحياة العملية المهنة ممثلة، ومُدرسة، وكاتبة سينا�...

Canadian Anishinaabekwe artist (born 1960) Rebecca BelmoreRebecca Belmore performing at Nuit Blanche 2016 in the Art Gallery of OntarioBorn (1960-03-22) March 22, 1960 (age 63)Upsala, Ontario, CanadaNationalityLac Seul First Nation (Canadian)Known forinstallation artist, Performance artistAwardsGovernor General's Award 2013Websiterebeccabelmore.com Rebecca Belmore RCA D.F.A. (born March 22, 1960) is a Canadian interdisciplinary Anishinaabekwe artist who is notable for politically co...

Prix d'architecture contemporaine de l'Union européenne Les lauréats du prix et de la mention spéciale reçoivent respectivement 60 000 et 20 000 euros et une sculpture évoquant le pavillon de Mies van der Rohe à Barcelone. Description Récompense tous les deux ans des œuvres architecturales exemplaires Organisateur Commission européenneFondation Mies van der Rohe Pays Union européenne Date de création 28 avril 1987 Dernier récipiendaire Lacaton & Vassal Architectes pour l...

Izalci Lucas Izalci LucasIzalci Lucas Senador pelo Distrito Federal Período 1º de fevereiro de 2019 até a atualidade Deputado Federal pelo Distrito Federal Período 29 de abril de 2008 até 1º de fevereiro de 2019 Deputado Distrital do Distrito Federal Período 1º de fevereiro de 2003 até 1º de fevereiro de 2007 Dados pessoais Nascimento 7 de abril de 1956 (67 anos) Araújos, MG Nacionalidade brasileiro Partido PSDB (1998-presente) Profissão Contador e Professor Izalci Lucas...

Kanselir agung (Tiongkok) Hanzi: 宰相 Alih aksara Mandarin - Hanyu Pinyin: Zǎixiàng - Wade-Giles: Tsai3-hsiang4 nama alternatif Hanzi: 丞相 Alih aksara Mandarin - Hanyu Pinyin: Chéngxiàng - Wade-Giles: Ch'eng2-hsiang4 Kanselir agung (宰相/丞相), sering juga diterjemahkan menjadi perdana menteri, penasihat kepala, kanselir, kepala dewan, kepala menteri, kanselir kekaisaran atau letnan kanselir, adalah pejabat eksekutif tertinggi dalam pemerintahan kekaisaran Tiongkok. Jabatan ini d...

Hans Krankl Informasi pribadiNama lengkap Johann KranklTanggal lahir 14 Februari 1953 (umur 70)Tempat lahir Wina, AustriaTinggi 1,82 m (5 ft 11+1⁄2 in)Posisi bermain StrikerKarier senior*Tahun Tim Tampil (Gol)1970–1978 Rapid Wien 205 (160)1971–1972 → Wiener AC (pinjaman) 26 (27)1978–1981 Barcelona 46 (34)1979–1980 → First Vienna (pinjaman) 17 (13)1981–1986 Rapid Wien 145 (107)1986–1988 Wiener AC 60 (40)1988 Kremser 5 (1)1989 Austria Salzburg 14 (10)To...
Artikel ini adalah bagian dari seri:Permainan video Pelantar Dingdong Konsol permainan Konsol video rumah Permainan elektronik Konsol genggam Permainan ponsel Permainan daring Permainan PC Linux Mac Genre Laga Berhantam Bertarung Arung pelantar Bertahan hidup Siluman Bertahan hidup horor Petualangan Bermain peran Bermain peran laga Bermain peran taktik Simulasi Konstruksi dan manajemen Simulasi kehidupan Olahraga Kendaraan Strategi Bertarung daring banyak pemain Strategi waktu nyata Taktik wa...

Not to be confused with Bank Rakyat Indonesia. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bank Rakyat – news · newspapers · books · scholar · JSTOR (July 2019) (Learn how and when to remove this template message) Bank Kerjasama Rakyat Malaysia BerhadTrade nameBank RakyatTypePublic limited companyIndustr...

HGCFull nameHOC Gazellen CombinatieNickname(s)De Gazellen (The Gazelles)Founded22 September 1906; 117 years ago (1906-09-22)Home groundDe Roggewoning, WassenaarLeagueMen's HoofdklasseWomen's Hoofdklasse2021–22Men: 4thWomen: 6thWebsiteClub website Home Away H.O.C. Gazellen-Combinatie, also known as HGC, is a Dutch professional field hockey club located in Wassenaar, South Holland on the border of The Hague. The club was founded on 22 September 1906.[1] The first tea...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari List of female Nobel laureates di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: p...

Untuk kegunaan lain, lihat Metis. 9 Metis PenemuanDitemukan olehAndrew GrahamTanggal penemuan25 April 1848PenamaanAsal namaMetisNama alternatif1974 QU2Kategori planet minorSabuk utamaKata sifat bahasa InggrisMetidianCiri-ciri orbit[1]Epos 14 Juli 2004(Kalender Julian 2453200,5)Aphelion400,548 Gm (2,678 SA)Perihelion313,556 Gm (2,096 SA)Sumbu semimayor357,052 Gm (2,387 SA)Eksentrisitas0,122Periode orbit1346,815 hr (3,69 a)Kecepatan orbit rata-rata19,2...

American composer Eric AllamanBackground informationBornSpringfield, MissouriGenresFilm score, musical theatre, balletOccupation(s)ComposerInstrument(s)PianoYears active1985–presentWebsitehttps://www.ericallaman.comMusical artist Eric Allaman is an American composer who has worked in film, television, theater and ballet. His career began when he co-composed the score to Ridley Scott's Legend with the German electronic group Tangerine Dream.[1] That opportunity led to Eric re-scoring...

حِسْمَى موقع تقريبي لصحراء حسمى الموقع البلد الأردن السعودية الإحداثيات 29°16′43″N 35°28′54″E / 29.278635°N 35.481684°E / 29.278635; 35.481684 الارتفاعات بيانات أخرى الأمطار ما بين 50-100 ملم. الموارد الطبيعية مياه جوفية المعالم وادي رم وجبل اللوز تعديل مصدري - تعديل صحراء حِسْمَى ه...

Alaskan Mayoral Election 1987 Anchorage mayoral election ← 1984 October 12, 1987 (first round)[1]November 3, 1987 (runoff)[2] 1990 → Turnout52.46% (runoff)[2] Candidate Tom Fink Dave Walsh H. A. Red Boucher First-round vote 15,666 18,200 12,346 First-round percentage 30.30% 35.20% 23.88% Second-round vote 30,962 23,214 Second-round percentage 57.15% 42.85% Candidate Larry Baker First-round vote 3,342 First-round percentage 6.46% Mayo...

Đừng nhầm lẫn với Bộ trưởng Bộ Ngoại giao Hoa Kỳ. Quan hệ đảng phái hoặc cơ quan chính phủ tương tự của Bang vụ khanh hiện nhiệm Hoa Kỳ: Bang vụ khanh đảng viên Dân Chủ Bang vụ khanh đảng viên Cộng hoà Bang vụ khanh độc lập Bang vụ khanh đảng viên Cộng hoà hoặc Đảng Tân tiến bộ Không thiết lập Bang vụ khanh Bang vụ khanh[1] (tiếng ...

Ancient city in southwest Asia Minor AndriakeἈνδριάκηAndriake Harbour areaShown within TurkeyLocationDemre, Antalya Province, TurkeyRegionLyciaCoordinates36°13′35″N 29°57′23″E / 36.22639°N 29.95639°E / 36.22639; 29.95639TypeAncient Settlement and port Andriake Plan Wikimedia Commons has media related to Andriake. Andriake or Andriaca (Ancient Greek: Ἀνδριάκη) was an ancient city and the port of the ancient town of Myra in Lycia. It is loca...

العلاقات الغامبية الكورية الشمالية غامبيا كوريا الشمالية غامبيا كوريا الشمالية تعديل مصدري - تعديل العلاقات الغامبية الكورية الشمالية هي العلاقات الثنائية التي تجمع بين غامبيا وكوريا الشمالية.[1][2][3][4][5] مقارنة بين البلدين هذه مقارن�...

Species of fly Rabdophaga rosariella Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Diptera Family: Cecidomyiidae Genus: Rabdophaga Species: R. rosariella Binomial name Rabdophaga rosariella(Kieffer, 1897) Rabdophaga rosariella is a species of gall midge which forms galls on sallows (Salix species). It was first described by Jean-Jacques Kieffer in 1897. Description The gall is a small rosette, most often in an axillary bud on sallo...