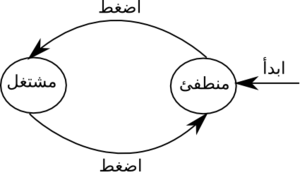
ظ†ط¸ط±ظٹط© ط§ظ„طھط´ط؛ظٹظ„ ط§ظ„ط°ط§طھظٹ
|
Read other articles:

1999 single by Jamiroquai SupersonicSingle by Jamiroquaifrom the album Synkronized B-sideSupersonic (remix)Released13 September 1999 (1999-09-13)[1]Length5:14 (album version)3:40 (radio edit)LabelSony Soho SquareSongwriter(s)Jay KayToby SmithDerrick McKenzieSola AkingbolaWallis BuchananSimon KatzProducer(s)Jay Kay, Al StoneJamiroquai singles chronology Canned Heat (1999) Supersonic (1999) King for a Day (1999) Music videoSupersonic on YouTube Supersonic is the third sin...

Group of chemical compounds Peganum harmala, commonly known as Syrian Rue Harmala alkaloids are several alkaloids that increase effects of reward system neurotransmitter dopamine by acting as monoamine oxidase inhibitors (MAOIs). These alkaloids are found in the seeds of Peganum harmala (also known as Harmal or Syrian Rue), as well as leaves of tobacco.[1] The alkaloids include harmine, harmaline, harmalol, and their derivatives, which have similar chemical structures, hence the name ...

هŒ—م‚ھم‚»مƒپم‚¢ه…±ه’Œه›½مپ®è،Œو”؟هŒ؛画(مپچمپںم‚ھم‚»مƒپم‚¢مپچم‚‡مپ†م‚ڈمپ“مپڈمپ®مپژم‚‡مپ†مپ›مپ„مپڈمپ‹مپڈ)مپ§مپ¯م€پمƒم‚·م‚¢é€£é‚¦مپ®هŒ—م‚ھم‚»مƒپم‚¢ه…±ه’Œه›½ï¼ˆهŒ—م‚ھم‚»مƒپم‚¢مƒ»م‚¢مƒ©مƒ‹مƒ¤ه…±ه’Œه›½ï¼‰مپ®è،Œو”؟هŒ؛ç”»مپ«مپ¤مپ„مپ¦è¨کè؟°مپ™م‚‹م€‚ è،Œو”؟هŒ؛ç”» هŒ—م‚ھم‚»مƒپم‚¢ه…±ه’Œه›½مپ®è،Œو”؟هŒ؛ç”» هŒ—م‚ھم‚»مƒپم‚¢ه…±ه’Œه›½مپ¯1مپ¤مپ®éƒ½ه¸‚ç®،هŒ؛م€پ8مپ®هœ°هŒ؛مپ‹م‚‰و§‹وˆگمپ•م‚Œم‚‹[1]م€‚ 都ه¸‚ç®،هŒ؛ م‚¦مƒ©م‚¸م‚«مƒ•م‚«م‚¹éƒ½ه¸‚ç®،هŒ؛ (ذ’ذ»ذ°ذ´ذ¸ذ؛ذ°ذ²ذ؛ذ°ذ·) (首都) هœ°هŒ؛(مƒ©مƒ¨مƒ³) م‚¢...

Overview of banana production in Belize Banana sorting in Belize. Banana production in Belize accounted for 16 percent of total Belizean exports in 1999.[1] Banana production was aided in the 1990s by privatization and market and production.[1] Banana production in Belize fluctuates, falling from 68,000 metric tons (67,000 long tons; 75,000 short tons) in 1994 to 45,000 (44,000; 50,000) in 1995 before rising back to 78,000 (77,000; 86,000) in 1999.[1] Banana production...

ظ‡ط°ظ‡ ط§ظ„ظ…ظ‚ط§ظ„ط© ظٹطھظٹظ…ط© ط¥ط° طھطµظ„ ط¥ظ„ظٹظ‡ط§ ظ…ظ‚ط§ظ„ط§طھ ط£ط®ط±ظ‰ ظ‚ظ„ظٹظ„ط© ط¬ط¯ظ‹ط§. ظپط¶ظ„ظ‹ط§طŒ ط³ط§ط¹ط¯ ط¨ط¥ط¶ط§ظپط© ظˆطµظ„ط© ط¥ظ„ظٹظ‡ط§ ظپظٹ ظ…ظ‚ط§ظ„ط§طھ ظ…طھط¹ظ„ظ‚ط© ط¨ظ‡ط§. (ظ…ط§ط±ط³ 2021) طط¯ط«طھ ط¹ط¯ط© طھظˆط³ط¹ط§طھ ط§ظ†طھط´ط± ظ…ظ† ط®ظ„ط§ظ„ظ‡ط§ ط§ظ„ط¥ظ†ط³ط§ظ† ط§ظ„ط¨ط¯ط§ط¦ظٹ (ط§ظ„ظ‡ظˆظ…ظˆ) ظ…ظ† ط£ظپط±ظٹظ‚ظٹط§ ظˆط¹ط¨ط± ط£ظ†طط§ط، ط£ظˆط±ط§ط³ظٹط§ ط®ظ„ط§ظ„ ط§ظ„ط¹طµط± ط§ظ„طط¬ط±ظٹ ط§ظ„ظ‚ط¯ظٹظ… ط§ظ„ط³ظپظ„ظٹطŒ ظˆططھظ‰ ط¨ط¯ط§ظٹط© ط§ظ„ط¹طµط± ط§ظ„طط¬ط±ظٹ ط§ظ„ظ‚ط¯ظٹظ… ط§ظ„ط£ظˆط³ط·...

Morton Everel Post Morton Everel Post (* 25. Dezember 1840 bei Rochester, New York; †19. Mأ¤rz 1933 in Alhambra, Kalifornien) war ein US-amerikanischer Politiker. Zwischen 1881 und 1885 vertrat er als Delegierter das Wyoming-Territorium im US-Reprأ¤sentantenhaus. Inhaltsverzeichnis 1 Frأ¼he Jahre und politischer Aufstieg 2 Post im US-Kongress 3 Weiterer Lebenslauf 4 Weblinks Frأ¼he Jahre und politischer Aufstieg Morton Post besuchte die أ¶ffentlichen Schulen seiner Heimat. Im Jahr 1860 zog...

Family of true bugs Acanaloniidae Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Hemiptera Suborder: Auchenorrhyncha Infraorder: Fulgoromorpha Superfamily: Fulgoroidea Family: AcanaloniidaeAmyot & Serville 1843 Acanaloniidae is a family of planthoppers. It is sometimes treated as a subfamily of Issidae (as Acanaloniinae).[1][2] Genera Genera include:[3] Acanalonia Spinola, 1839 Aylaella Demir & أ–zdikmen, ...

ظٹظپطھظ‚ط± ظ…ططھظˆظ‰ ظ‡ط°ظ‡ ط§ظ„ظ…ظ‚ط§ظ„ط© ط¥ظ„ظ‰ ط§ظ„ط§ط³طھط´ظ‡ط§ط¯ ط¨ظ…طµط§ط¯ط±. ظپط¶ظ„ط§ظ‹طŒ ط³ط§ظ‡ظ… ظپظٹ طھط·ظˆظٹط± ظ‡ط°ظ‡ ط§ظ„ظ…ظ‚ط§ظ„ط© ظ…ظ† ط®ظ„ط§ظ„ ط¥ط¶ط§ظپط© ظ…طµط§ط¯ط± ظ…ظˆط«ظˆظ‚ ط¨ظ‡ط§. ط£ظٹ ظ…ط¹ظ„ظˆظ…ط§طھ ط؛ظٹط± ظ…ظˆط«ظ‚ط© ظٹظ…ظƒظ† ط§ظ„طھط´ظƒظٹظƒ ط¨ظ‡ط§ ظˆط¥ط²ط§ظ„طھظ‡ط§. (ظپط¨ط±ط§ظٹط± 2023) ظ‡ط°ظ‡ ط§ظ„ظ…ظ‚ط§ظ„ط© ط¹ظ† ط§طھطط§ط¯ ط§ظ„ط¨ظˆط³ظ†ط© ظˆط§ظ„ظ‡ط±ط³ظƒ. ظ„ظ…ط¹ط§ظ†ظچ ط£ط®ط±ظ‰طŒ ط·ط§ظ„ط¹ ط§ظ„ط¨ظˆط³ظ†ط© ظˆط§ظ„ظ‡ط±ط³ظƒ (طھظˆط¶ظٹط). ط§طھطط§ط¯ ط§ظ„ط¨ظˆط³ظ†ط© ظˆط§ظ„ظ...

ط´ط±ظƒط© ط§ظ„ط®ط·ظˆط· ط§ظ„ط³ط¹ظˆط¯ظٹط© ظ„طھظ†ظ…ظٹط© ظˆطھط·ظˆظٹط± ط§ظ„ط¹ظ‚ط§ط±ط´ط±ظƒط© ط§ظ„ط®ط·ظˆط· ط§ظ„ط³ط¹ظˆط¯ظٹط© ظ„طھظ†ظ…ظٹط© ظˆطھط·ظˆظٹط± ط§ظ„ط¹ظ‚ط§ط± ط³ط§ط±ط¯ط§ظ„ط´ط¹ط§ط±ظ…ط¹ظ„ظˆظ…ط§طھ ط¹ط§ظ…ط©ط§ظ„ظ†ظˆط¹ ط´ط±ظƒط© ط³ط¹ظˆط¯ظٹط© ظ…ط³ط§ظ‡ظ…ط©ط§ظ„ظ…ظ‚ط± ط§ظ„ط±ط¦ظٹط³ظٹ ط§ظ„ط³ط¹ظˆط¯ظٹط©طŒ ط¬ط¯ط©ط§ظ„ظ…ظ†ط¸ظˆظ…ط© ط§ظ„ط§ظ‚طھطµط§ط¯ظٹط©ط§ظ„ط´ط±ظƒط© ط§ظ„ط£ظ… ظ…ط¬ظ…ظˆط¹ط© ط§ظ„ط®ط·ظˆط· ط§ظ„ط³ط¹ظˆط¯ظٹط© ط§ظ„ظ‚ط§ط¨ط¶ط©ط§ظ„ط®ط¯ظ…ط§طھ ط§ظ„طھط·ظˆظٹط± ط§ظ„ط¹ظ‚ط§ط±ظٹط§ظ„طµظ†ط§ط¹ط© ط§ظ„ط¹ظ‚ط§ط±ظ…ظ†ط§ط·ظ‚...

ذ›ذ°ذ¼ذ±ذµر€ر‚ ذ¸ذ· ذ،ذµذ½ر‚-ذذ¼ذµر€ذ°ذ»ذ°ر‚. Lambertus Audomarensis ذ”ذ°ر‚ذ° ر€ذ¾ذ¶ذ´ذµذ½ذ¸رڈ ذ¾ذ؛ذ¾ذ»ذ¾ 1061[1] ذ”ذ°ر‚ذ° رپذ¼ذµر€ر‚ذ¸ ذ¾ذ؛ذ¾ذ»ذ¾ 1125[1] ذ ذ¾ذ´ ذ´ذµرڈر‚ذµذ»رŒذ½ذ¾رپر‚ذ¸ ذ¼ذ¾ذ½ذ°ر… ذ¸ ر…ر€ذ¾ذ½ذ¸رپر‚ ذ›ذ°ذ¼ذ±ذµر€ر‚ ذ،ذµذ½ر‚-ذذ¼ذµر€رپذ؛ذ¸ذ¹ ذ·ذ° ر€ذ°ذ±ذ¾ر‚ذ¾ذ¹. ذœذ¸ذ½ذ¸ذ°ر‚رژر€ذ° ذ°ذ²ر‚ذ¾ر€رپذ؛ذ¾ذ¹ ر€رƒذ؛ذ¾ذ؟ذ¸رپذ¸ آ«Liber Floridusآ» ذ¸ذ· ذ±ذ¸ذ±ذ»ذ¸ذ¾ر‚ذµذ؛ذ¸ ذ“ذµذ½ر‚رپذ؛ذ¾ذ³ذ¾ رƒذ½ذ¸ذ²ذµر€رپذ¸ر‚ذµر‚ذ° (1121) ذ›ذ°ذ¼ذ±ذµر€ر‚ ذ¸ذ· ذ،ذµذ½ر‚-ذ...

Philippine-related events during the year of 1963 ← 1962 1961 1960 1963 in the Philippines → 1964 1965 1966 Decades: 1940s 1950s 1960s 1970s 1980s See also: List of years in the Philippines films 1963 in the Philippines details events of note that happened in the Philippines in the year 1963. Incumbents President Diosdado Macapagal President: Diosdado Macapagal (Liberal) Vice President: Emmanuel Pelaez (Liberal) Chief Justice: Cأ©sar Bengzon Congress: 5th Events April April 5 – ...

Gaya atau nada penulisan artikel ini tidak mengikuti gaya dan nada penulisan ensiklopedis yang diberlakukan di Wikipedia. Bantulah memperbaikinya berdasarkan panduan penulisan artikel. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Poedjono PranyotoWakil Ketua Majelis Permusyawaratan Rakyat(Utusan Daerah)Masa jabatan3 Oktober 1997 – 1 Oktober 1999PresidenSoeharto B.J. HabibiePendahuluYasir HadibrotoPenggantiOesman Sapta OdangGubernur Lampung ke-5Masa jabata...

Rallycross series held in Latvia World RX layout of Biؤ·ernieku Kompleksؤپ Sporta Bؤپze The 2016 Euro RX of Latvia was the eighth round of the forty-first season of the FIA European Rallycross Championship. The event was held at the Biؤ·ernieku Kompleksؤپ Sporta Bؤپze in Riga, Latvia as an undercard to the 2016 World RX of Latvia and was contested by the Supercar (fifth and final round) and Super1600 (fourth round) classes. It was the first ever European Rallycross round held in Latvia.[1...

Institutional corruption in the country Political corruption Concepts Anti-corruption Bribery Cronyism Economics of corruption Electoral fraud Elite capture Influence peddling Kleptocracy Mafia state Nepotism Slush fund Simony Corruption by country Africa Angola Botswana Cameroon Chad Comoros Congo Egypt Equatorial Guinea Eritrea Ethiopia Ghana Guinea-Bissau Kenya Liberia Mauritius Morocco Nigeria Senegal Sierra Leone Somalia South Africa South Sudan Sudan Tanzania Tunisia Uganda Zambia Zimba...

Canadian curler Jamie KoeCurlerBorn (1977-11-03) November 3, 1977 (age 46)Yellowknife, Northwest TerritoriesTeamCurling clubYellowknife CC, YellowknifeSkipJamie KoeThirdGlen KennedySecondCole ParsonsLeadShadrach McleodAlternateRobert BordenCurling career Member Association Northwest TerritoriesBrier appearances16 (2006, 2007, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2022, 2023)Top CTRS ranking17th (2003–04) Medal record Representing Northwest T...

4. Etappe der Tour de France 2023 AllgemeinesEtappe4. EtappeطŒ Tour de France 2023Streckentyp FlachetappeDatum4. Juli 2023Etappenlأ¤nge181,8 kmLand FrankreichStartDaxZielNogaroFahrer am Start174Fahrer am Ziel174Durchschnittsآgeschwindigkeit41,089 km/hHأ¶henmeter1.434 mErgebnis1. Jasper Philipsen4 h 25 min 28 s(Alpecin-Deceuninck)2. Caleb Ewan+ 0 s(Lotto Dstny)3. Phil Bauhaus+ 0 s(Bahrain Victorious) Benoأ®t Cosnefroy(AG2R Citroأ«n Team)Stand in der Gesamtwertung Adam Yates 18 h 18 min 01 s(U...

7 ر‚ر€ذ°ذ²ذ½رڈ 2010 ر€ذ¾ذ؛رƒ, ذ² ذ؟ذµر€ذµذ´ذ´ذµذ½رŒ آ«9 ر‚ر€ذ°ذ²ذ½رڈآ», ذ؟ذµر€ذµذ´ ذ؟ذ¾ر‡ذ°ر‚ذ؛ذ¾ذ¼ ر–ذ½ر‚ذµر€ذ²'رژ آ«ذکذ·ذ²ذµرپر‚ذ¸رڈذ¼آ»[1] ذ³ذ¾ذ»ذ¾ذ²ذ½ذ¸ذ¹ ر€ذµذ´ذ°ذ؛ر‚ذ¾ر€ ذ³ذ°ذ·ذµر‚ذ¸ ذ’ر–ر‚ذ°ذ»ر–ذ¹ ذگذ±ر€ذ°ذ¼ذ¾ذ² ذ؟ذ¾ذ´ذ°ر€رƒذ²ذ°ذ² ذ”ذ¼ذ¸ر‚ر€رƒ ذœذµذ´ذ²ذµذ´ر”ذ²رƒ ذ·ذ½ر–ذ¼ذ؛ذ¸ ذ؟ذµر€رˆذ¾ر— ذ؛ذ¾ر€ذµرپذ؟ذ¾ذ½ذ´ذµذ½ر†ر–ر— ذںذ°ذ²ذ»ذ° ذ¢ر€ذ¾رˆذ؛ر–ذ½ذ°. ذ¢ذ°ذ؛ذ¸ذ¹ ر…ر–ذ´ ذ² ر€ذ¾ذ±ذ¾ر‚ر– ذ—ذœذ† ذ؟ذ¾ذ²ذ¸ذ½ذµذ½ رپذ¸ذ¼ذ²ذ¾ذ»ر–ذ·رƒذ²ذ°ر‚ذ¸[ذ؟ر€ذ¸ذ¼. 1] ذ´ذ»رڈ ذ°رƒذ´ذ¸ر‚ذ¾ر€ر–ر— ذ·ذ½ذ...

This article is about the film. For other uses, see First Night (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1st Night – news آ· newspapers آ· books آ· scholar آ· JSTOR (May 2013) (Learn how and when to remove this template message) 2010 film1st NightDirected byChristopher MenaulStarringRich...

ط¥ظٹط±ظˆ ظ…ط§ط±ظƒط§ظ†ظٹظ† ظ…ط¹ظ„ظˆظ…ط§طھ ط´ط®طµظٹط© ط§ظ„ظ…ظٹظ„ط§ط¯ 3 ظٹظˆظ„ظٹظˆ 1991 (32 ط³ظ†ط©) ظٹظˆظپط§ط³ظƒظˆظ„ط§ ط§ظ„ط·ظˆظ„ 1.97 ظ… (6 ظ‚ط¯ظ… 5 1⁄2 ط¨ظˆطµط©) ظ…ط±ظƒط² ط§ظ„ظ„ط¹ط¨ ظ…ظ‡ط§ط¬ظ… ط§ظ„ط¬ظ†ط³ظٹط© ظپظ†ظ„ظ†ط¯ط§ ط§ظ„ط£ط¨ ط¨ظٹظƒط§ ظ…ط§ط±ظƒط§ظ†ظٹظ† ط£ط®ظˆط© ظˆط£ط®ظˆط§طھ ظ„ط§ظˆط±ظ‰ ظ…ط§ط±ظƒط§ظ†ظٹظ† ظ…ط¹ظ„ظˆظ…ط§طھ ط§ظ„ظ†ط§ط¯ظٹ ط§ظ„ظ†ط§ط¯ظٹ ط§ظ„طط§ظ„ظٹ ط§طھط´ ط¢ظٹ ط§ظپ ظƒظٹ ط§ظ„ط±ظ‚ظ… 9 ظ…ط³ظٹط±ط© ط§ظ„ط´ط¨ط§ط¨ ط³ظ†ظˆط§طھ ظپط±ظ...

Aguada de Cima Freguesia Escudo Aguada de CimaLocalizaciأ³n de Aguada de Cima en Portugal Coordenadas 40آ°31′19″N 8آ°25′42″O / 40.522027777778, -8.4283055555556Entidad Freguesia • Paأs Portugal • Municipio أپguedaSuperficie • Total 27.55 kmآ²Altitud • Media 41 m s. n. m.Poblaciأ³n (2001) • Total 3952 hab. • Densidad 143,4 hab/kmآ²Huso horario UTCآ±00:00Cأ³digo postal 3750[1]Patrono(a...